【数学建模】--灰色关联分析
系统分析:
一般的抽象系统,如社会系统,经济系统,农业系统,生态系统,教育系统等都包含有许多种因素,多种因素共同作用的结果决定了该系统的发展态势。人们常常希望知道在众多的因素中,哪些是主要因素,哪些是次要因素;哪些因素对系统发展影响大,哪些因素对系统发展影响小;那些因素对系统发展起推动作用需强化发展;那些因素对系统发展起阻碍作用需加以抑制;……这些都是系统分析中人们普遍关心的问题。例如,粮食生产系统,人们希望提高粮食总产量,而影响粮食总产量的因素是多方面的,有播种面积以及水利,化肥,土壤,种子,劳力,气候,耕作技术和政策环境等。为了实现少投入多产出,并取得良好的经济效益,社会效益和生态效益,就必须进行系统分析。
数理统计的不足之处:
灰色关联的基本思想:
灰色关联分析原理:灰色关联分析(Grey Relational Analysis)是一种用于研究变量之间关联性的方法,特别适用于样本数据较少、样本特征缺失或数据质量不高的情况下。它是由灰色系统理论发展而来,旨在分析和描述变量之间的关联程度。
在灰色关联分析中,首先将各个变量的数据进行数值化,常采用标准化或归一化的方法,将变量的取值范围转化为[0, 1]之间。然后,通过计算变量之间的关联度,确定它们之间的关联程度。
灰色关联分析的步骤主要包括以下几个方面:
1.数据标准化:将原始数据进行标准化处理,通常采用归一化或标准化方法,使得各个变量具有相同的数值范围。
2.构建关联系数矩阵:计算各个变量之间的关联系数,一般采用灰色关联度或灰色斜率关联度。关联系数表示了变量之间的相对关联程度。
3.确定关联度序列:根据计算得到的关联系数,确定关联度序列,即将各个变量按照关联度的大小排序。
4.确定关联度权重:根据关联度序列,计算关联度权重,即各个变量在总关联系数中的贡献比例。
5.计算灰色关联度:通过将各个变量的关联系数与关联度权重相乘,并进行累加,计算出灰色关联度。灰色关联度可以反映变量之间的关联程度。
通过灰色关联度的计算,可以得到各个变量之间的关联情况,进而进行数据分析和决策支持。灰色关联分析常被应用于多个领域,包括经济、管理、环境、工程等,用于评估指标之间的关联强度、寻找关键因素等。
需要注意的是,灰色关联分析的结果是相对的,不具备精确的定量意义,应结合实际问题和其他分析方法进行综合评估和判断。
例题以及Excel的实操: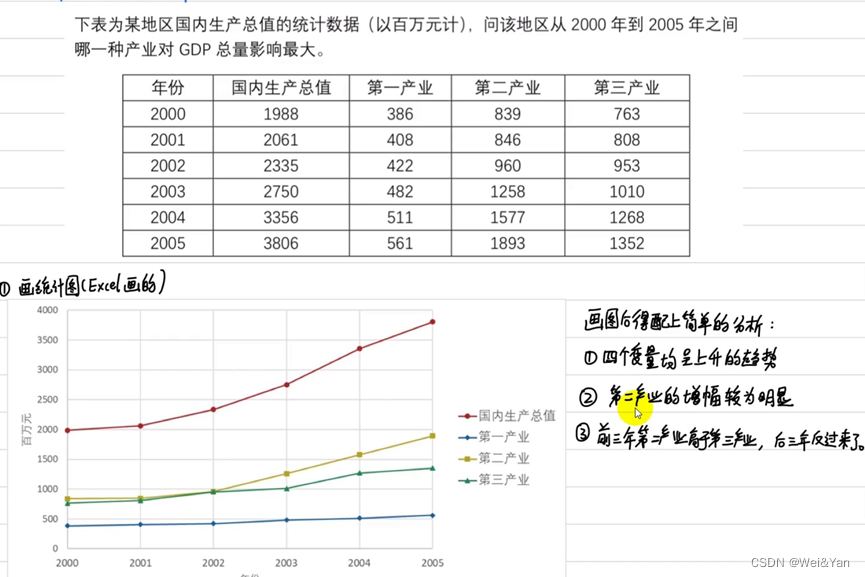 在excel中选择数据-插入-推荐图标-修改信息。
在excel中选择数据-插入-推荐图标-修改信息。
2.确定分析数列:
母序列:能反映系统特征值的数据序列,类似于因变量Y,此处记为X0
子序列:有影响系统行为的因素组成的数据序列。类似于自变量x,此处记为(x1,x2……xm)
3.对变量进行预处理:
目的:去量纲,缩小变量范围简化计算。
方法:每个元素/所在列的列向量的均值。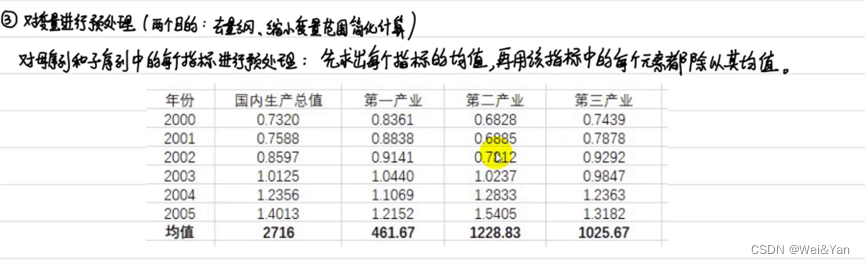
4.计算子序列中各个指标与母序列的关联系数
先求每子列元素与母列之间差的绝对值,在求出矩阵中所有元素的最小值a和最大值b。且取分辨系数p/rho=0.5
在通过公式计算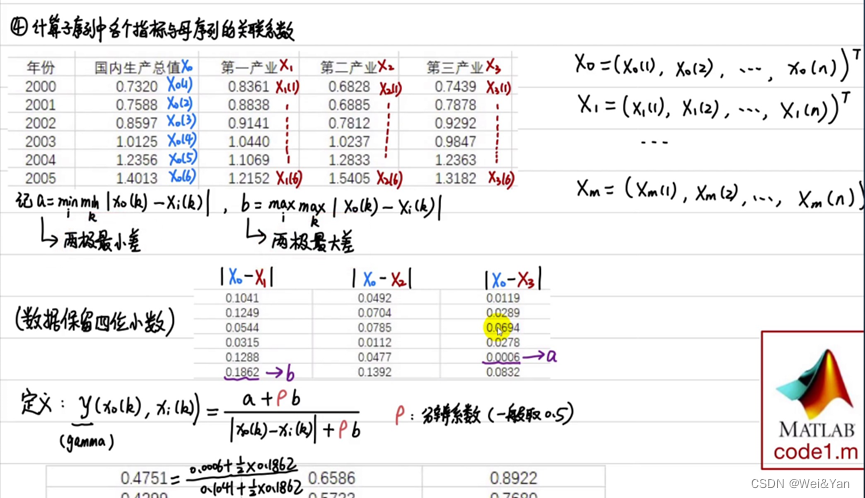
5.求灰色关联度:
公式:每列子序列与母序列关联系数的均值。
6.分析结果进行总结。
MATLAB代码实现:
参考代码:
%% 灰色关联分析用于系统分析例题的讲解
clear;clc
load gdp.mat % 导入数据 一个6*4的矩阵
% 不会导入数据的同学可以看看第二讲topsis模型,我们也可以自己在工作区新建变量,并把Excel的数据粘贴过来
% 注意Matlab的当前文件夹一定要切换到有数据文件的这个文件夹内
Mean = mean(gdp); % 求出每一列的均值以供后续的数据预处理
gdp = gdp ./ repmat(Mean,size(gdp,1),1); %size(gdp,1)=6, repmat(Mean,6,1)可以将矩阵进行复制,复制为和gdp同等大小,然后使用点除(对应元素相除),这些在第一讲层次分析法都讲过
disp('预处理后的矩阵为:'); disp(gdp)
Y = gdp(:,1); % 母序列
X = gdp(:,2:end); % 子序列
absX0_Xi = abs(X - repmat(Y,1,size(X,2))) % 计算|X0-Xi|矩阵(在这里我们把X0定义为了Y)
a = min(min(absX0_Xi)) % 计算两级最小差a
b = max(max(absX0_Xi)) % 计算两级最大差b
rho = 0.5; % 分辨系数取0.5
gamma = (a+rho*b) ./ (absX0_Xi + rho*b) % 计算子序列中各个指标与母序列的关联系数
disp('子序列中各个指标的灰色关联度分别为:')
disp(mean(gamma))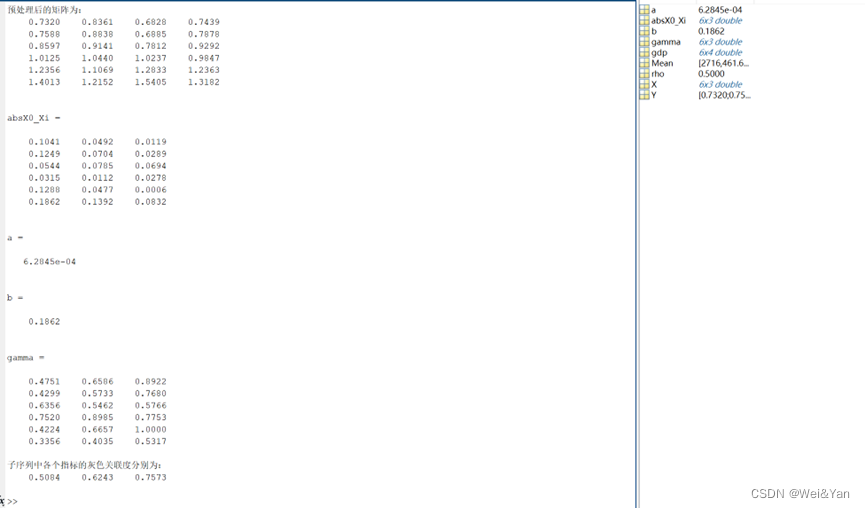
讨论:
灰色分析用于综合评价问题: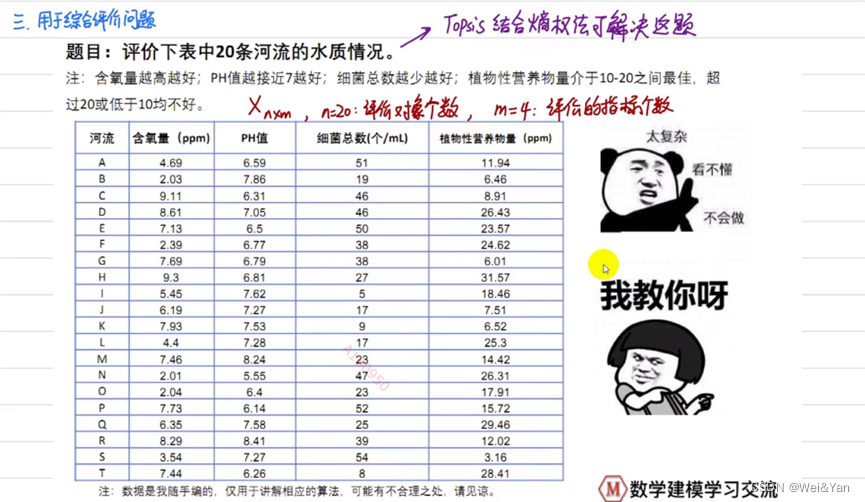
步骤:
MATLAB代码实现:
这里的代码和博主之前TOPSIS算法一文:数学建模——TOPSIS法_Wei&Yan的博客-CSDN博客
前面的操作都一致,只是在最后添加上了灰色相关分析的方法
步骤:
- 先对矩阵进行预处理:每个元素/所在列的均值
- 构造母序列和子序列
母序列:取每一行的max构成一个列向量
子序列:预处理后的矩阵
3.计算灰色关联度
先求每个元素与母序列差的绝对值矩阵,再求两级最大/小差。
最后利用公式求灰色关联度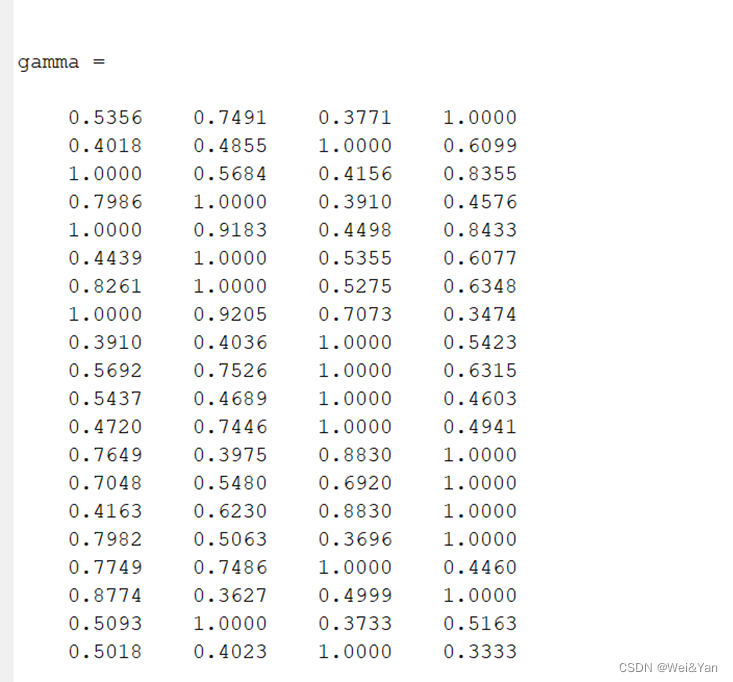
4.求权重:每列的均值/每列均值的和
5.求得分:(矩阵中每个元素*其所在列的权重)的矩阵的列和。(得到一个)
6.归一化得分:每个元素/向量和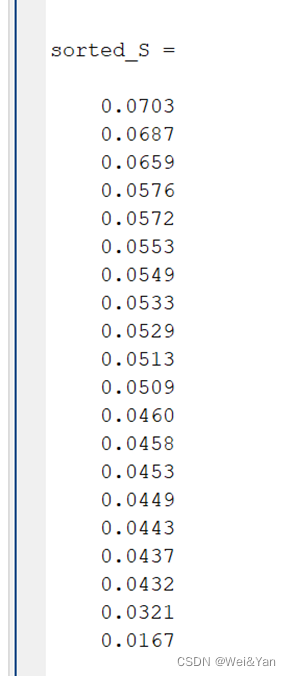
图形对比: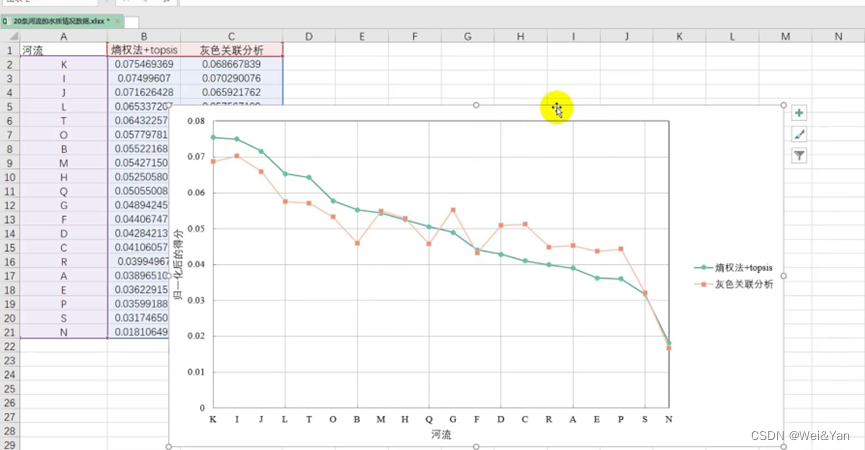
参考代码:
这里只参考了主函数加上带有灰色相关分析的代码,其他自定义函数可参考博主原来的文章TOPSIS算法:数学建模——TOPSIS法_Wei&Yan的博客-CSDN博客
%% 灰色关联分析用于综合评价模型例题的讲解
clear;clc
load data_water_quality.mat
% 不会导入数据的同学可以看看第二讲topsis模型,我们也可以自己在工作区新建变量,并把Excel的数据粘贴过来
% 注意Matlab的当前文件夹一定要切换到有数据文件的这个文件夹内%% 判断是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标'])
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理,需要请输入1 ,不需要输入0: ']); %1if Judge == 1Position = input('请输入需要正向化处理的指标所在的列,例如第2、3、6三列需要处理,那么你需要输入[2,3,6]: '); %[2,3,4]disp('请输入需要处理的这些列的指 标类型(1:极小型, 2:中间型, 3:区间型) ')Type = input('例如:第2列是极小型,第3列是区间型,第6列是中间型,就输入[1,3,2]: '); %[2,1,3]% 注意,Position和Type是两个同维度的行向量for i = 1 : size(Position,2) %这里需要对这些列分别处理,因此我们需要知道一共要处理的次数,即循环的次数X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));% Positivization是我们自己定义的函数,其作用是进行正向化,其一共接收三个参数% 第一个参数是要正向化处理的那一列向量 X(:,Position(i)) 回顾上一讲的知识,X(:,n)表示取第n列的全部元素% 第二个参数是对应的这一列的指标类型(1:极小型, 2:中间型, 3:区间型)% 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列% 该函数有一个返回值,它返回正向化之后的指标,我们可以将其直接赋值给我们原始要处理的那一列向量enddisp('正向化后的矩阵 X = ')disp(X)
end%% 对正向化后的矩阵进行预处理
Mean = mean(X); % 求出每一列的均值以供后续的数据预处理
Z = X ./ repmat(Mean,size(X,1),1);
disp('预处理后的矩阵为:'); disp(Z)%% 构造母序列和子序列
Y = max(Z,[],2); % 母序列为虚拟的,用每一行的最大值构成的列向量表示母序列
X = Z; % 子序列就是预处理后的数据矩阵%% 计算得分
absX0_Xi = abs(X - repmat(Y,1,size(X,2))) % 计算|X0-Xi|矩阵
a = min(min(absX0_Xi)) % 计算两级最小差a
b = max(max(absX0_Xi)) % 计算两级最大差b
rho = 0.5; % 分辨系数取0.5
gamma = (a+rho*b) ./ (absX0_Xi + rho*b) % 计算子序列中各个指标与母序列的关联系数
weight = mean(gamma) / sum(mean(gamma)); % 利用子序列中各个指标的灰色关联度计算权重
score = sum(X .* repmat(weight,size(X,1),1),2); % 未归一化的得分
stand_S = score / sum(score); % 归一化后的得分
[sorted_S,index] = sort(stand_S ,'descend') % 进行排序相关文章:

【数学建模】--灰色关联分析
系统分析: 一般的抽象系统,如社会系统,经济系统,农业系统,生态系统,教育系统等都包含有许多种因素,多种因素共同作用的结果决定了该系统的发展态势。人们常常希望知道在众多的因素中,哪些是主要…...

图像像素梯度
梯度 在高数中,梯度是一个向量,是有方向有大小。假设一二元函数f(x,y),在某点的梯度有: 结果为: 即方向导数。梯度的方向是函数变化最快的方向,沿着梯度的方向容易找到最大值。 图像梯度 在一幅模糊图…...

[论文笔记]Batch Normalization
引言 本文是论文神作Batch Normalization的阅读笔记,这篇论文引用量现在快50K了。 由于上一层参数的变化,导致每层输入的分布会在训练期间发生变化,让训练深层神经网络很复杂。这会拖慢训练速度,因为需要更低的学习率并小心地进行参数初始化,使得很难训练这种具有非线性…...

SpringCloud教程(中)
目录 八、Hystrix(服务降级) 8.1、Hystrix基本概念 8.1.1、分布式系统面临的问题 8.1.2、Hystrix是什么? 8.1.3、服务降级 概念 哪些情况会触发降级 8.1.4、服务熔断 8.1.5、服务限流 8.2、Hystrix案例 8.2.1、Hystrix支付微服务构…...

蓝帽杯2022
计算机取证 1 内存取证获取开机密码 现对一个windows计算机进行取证,请您对以下问题进行分析解答。 从内存镜像中获得taqi7的开机密码是多少?(答案参考格式:abcABC123) 首先我们直接对 1.dmp 使用 vol查看 py -2 v…...

vue + el-table 表格数据导出为excel表格
下载依赖 npm install --save xlsx file-saver引入插件 import * as XLSX from xlsx; import FileSaver from "file-saver";完整代码 <template><div class"administrativeCase-container"><div class"content-box"><di…...

ClickHouse(二十):Clickhouse SQL DDL操作-2-分区表DDL操作
进入正文前,感谢宝子们订阅专题、点赞、评论、收藏!关注IT贫道,获取高质量博客内容! 🏡个人主页:含各种IT体系技术,IT贫道_Apache Doris,大数据OLAP体系技术栈,Kerberos安全认证-CSDN博客 &…...
Springboot 在 redis 中使用 Guava 布隆过滤器机制
一、导入SpringBoot依赖 在pom.xml文件中,引入Spring Boot和Redis相关依赖 <!-- Google Guava 使用google的guava布隆过滤器实现--><dependency><groupId>com.google.guava</groupId><artifactId>guava</artifactId><vers…...
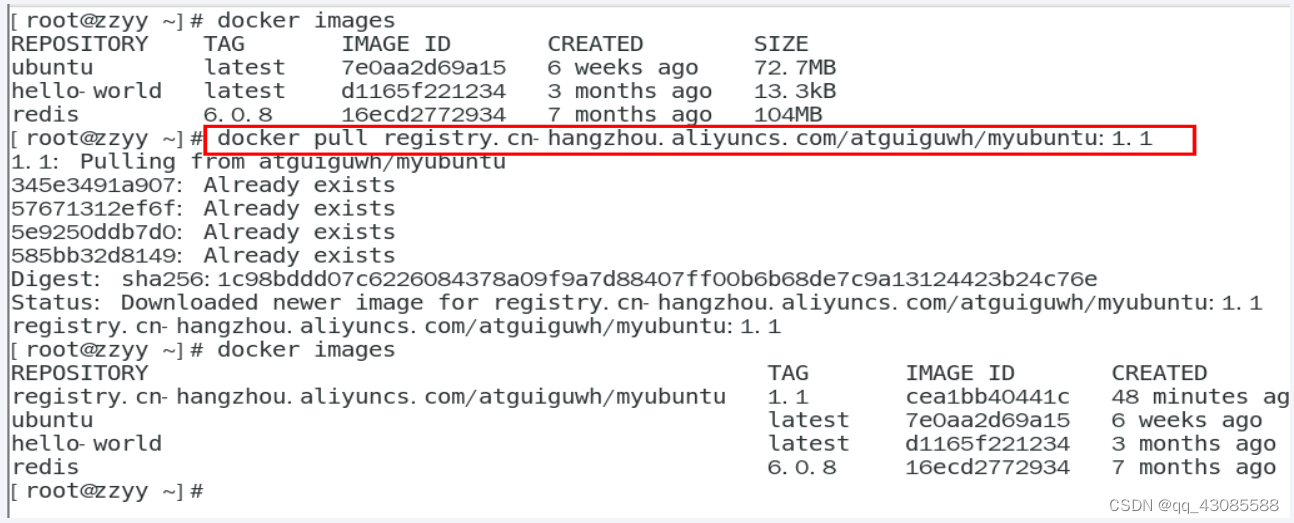
Docker本地镜像发布到阿里云
1. 本地镜像发布到阿里云 2. 镜像的生成方法 OPTIONS说明: -a :提交的镜像作者; -m :提交时的说明文字; 本次案例centosubuntu两个,当堂讲解一个,家庭作业一个,请大家务必动手,亲自实操。 docke…...
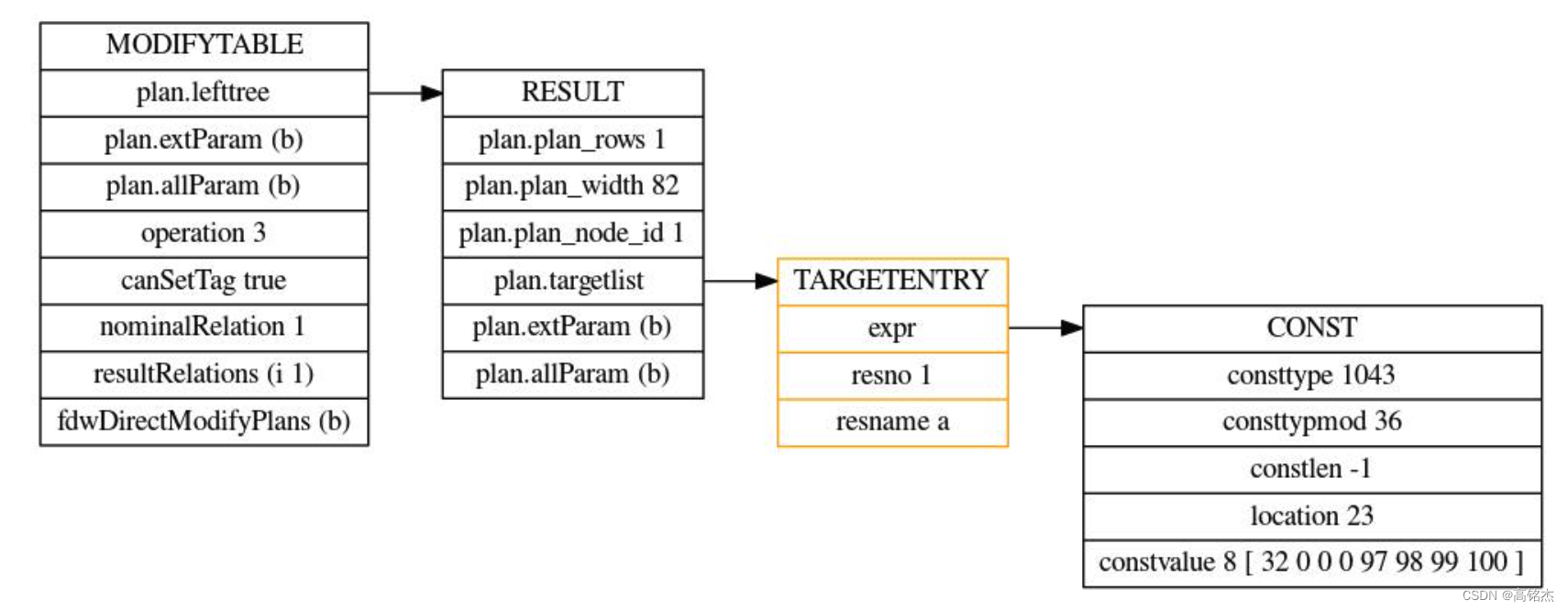
Postgresql源码(112)plpgsql执行sql时变量何时替换为值
相关 《Postgresql源码(41)plpgsql函数编译执行流程分析》 《Postgresql源码(46)plpgsql中的变量类型及对应关系》 《Postgresql源码(49)plpgsql函数编译执行流程分析总结》 《Postgresql源码(5…...

OhemCrossEntropyLoss
1. Ohem Cross Entropy Loss 的定义 OhemCrossEntropyLoss 是一种用于深度学习中目标检测任务的损失函数,它是针对不平衡数据分布和困难样本训练的一种改进版本的交叉熵损失函数。Ohem 表示 “Online Hard Example Mining”,意为在线困难样本挖掘。在目…...

prometheusalert区分告警到不同钉钉群
方法一 修改告警规则 - alert: cpu使用率大于88%expr: instance:node_cpu_utilization:ratio * 100 > 88for: 5mlabels:severity: criticallevel: 3kind: CpuUsageannotations:summary: "cpu使用率大于85%"description: "主机 {{ $labels.hostname }} 的cp…...
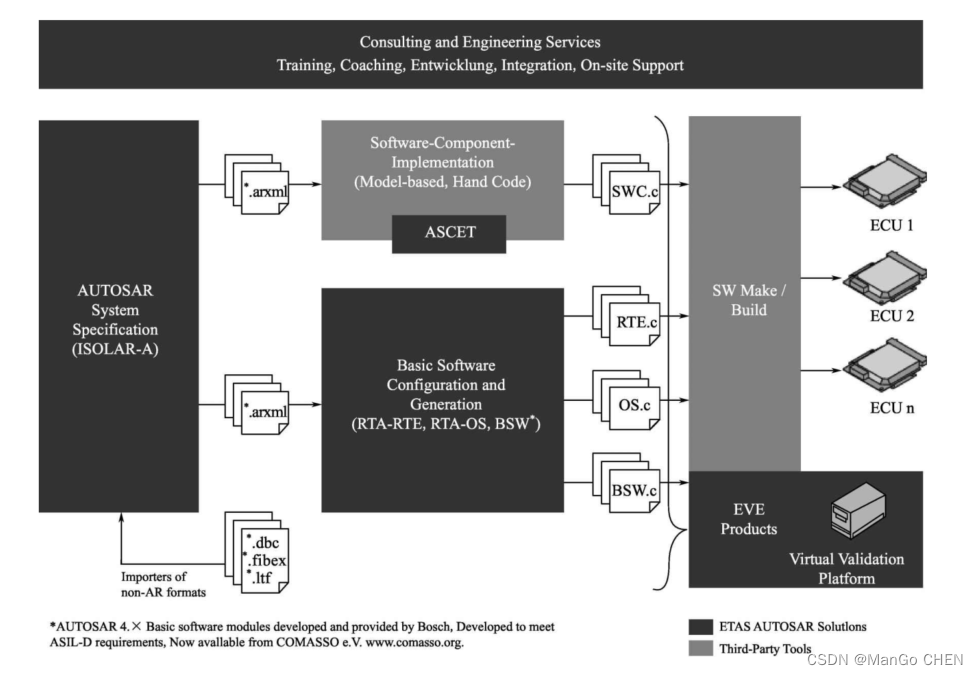
AUTOSAR规范与ECU软件开发(实践篇)3.2 ETAS AUTOSAR系统解决方案介绍(上)
1、ETAS AUTOSAR系统解决方案介绍 博世集团ETAS公司基于其强大的研发实力为用户提供了一套高效、 可靠的AUTOSAR系统解决方案, 该方案覆盖了软件架构设计、 应用层模型设计、 基础软件开发、 软件虚拟验证等各个方面, 如图3.5所示, 其中深色…...

【leetcode】第三章 哈希表part02
454.四数相加II public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {HashMap<Integer,Integer> map new HashMap<>();// 统计频率for (int i 0; i < nums1.length; i) {for (int j 0; j < nums2.length; j) {int num nums1…...
【C语言】memset()函数
一.memset()函数简介 我们先来看一下cplusplus.com - The C Resources Network网站上memset()函数的基本信息: 1.函数功能 memset()函数的功能是:将一块内存空间的每个字节都设置为指定的值。 这个函数通常用于初始化一个内存空间,或者清空一个内存空间…...
、重写(override,也叫做“覆盖”)和重定义(redefine,也叫作“隐藏”)的区别?)
C++中重载(overload)、重写(override,也叫做“覆盖”)和重定义(redefine,也叫作“隐藏”)的区别?
在C中,允许在同一作用域中的某个函数和运算符指定多个定义,分别称为函数重载和运算符重载。 重载声明是指一个与之前已经在该作用域内声明过的函数或方法具有相同名称的声明,但是它们的参数列表和定义(实现)不相同。 …...

将非受信数据作为参数传入,可能引起xml 注入,引起数据覆盖,这个问题咋解决
目录 1 解决 1 解决 当将非受信数据作为参数传入时,确实存在XML注入(XML Injection)的风险,攻击者可以通过构造恶意的XML数据来修改XML文档结构或执行意外的操作。为了解决这个问题,你可以采取以下措施: 输…...

设计模式-简单工厂模式
简单工厂模式又称为静态工厂模式,其实就是根据传入参数创建对应具体类的实例并返回实例对象,这些类通常继承至同一个父类,该模式专门定义了一个类来负责创建其他类的实例。 using System.Collections; using System.Collections.Generic; us…...

Maven框架SpringBootWeb简单入门
一、Maven ★ Maven:是Apache旗下的一个开源项目,是一款用于管理和构建java项目的工具。 官网:https://maven.apache.org/ ★ Maven的作用: 1. 依赖管理:方便快捷的管理项目依赖的资源(jar包),避免版本冲突问题。 2. 统一项目结构:提供标准、统一的项目结构。 …...

关于2023年8月19日PMP认证考试准考信下载通知
各位考生: 为保证参加2023年8月19日PMI项目管理资格认证考试的每位考生都能顺利进入考场参加考试,请完整阅读本通知内容。 一、关于准考信下载 为确保您顺利进入考场参加8月份考试,请及时登录本网站(https://event.chinapmp.cn/)…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
