vue-photo-preview( 照片预览功能 )
安装
npm install vue-photo-preview --save引入项目
import preview from 'vue-photo-preview'
import 'vue-photo-preview/dist/skin.css'let options = {fullscreenEl: false //是否可以全屏预览
};
Vue.use(preview, options)如果不写options 和 Vue.use(preview,options),那么默认具有全屏预览的功能Vue.use(preview)html代码
//在img标签添加preview属性 preview值相同即表示为同一组
<img src="xxx.jpg" preview="0" preview-text="描述文字">//分组
<img src="xxx.jpg" preview="1" preview-text="描述文字">
<img src="xxx.jpg" preview="1" preview-text="描述文字"><img src="xxx.jpg" preview="2" preview-text="描述文字">
<img src="xxx.jpg" preview="2" preview-text="描述文字">重点注意
在获取异步数据的时候可能遇到的问题
解决方法:
如果数据是异步获取回来的,会出现不管你怎么点击,都不会出现效果。这就需要在你成功获取数据回来之后,加上 this.$previewRefresh() ,刷新重置一下。
相关文章:
)
vue-photo-preview( 照片预览功能 )
安装 npm install vue-photo-preview --save 引入项目 import preview from vue-photo-preview import vue-photo-preview/dist/skin.csslet options {fullscreenEl: false //是否可以全屏预览 }; Vue.use(preview, options)如果不写options 和 Vue.use(preview,options)&…...

Angular 独立组件入门
Angular 独立组件入门 如果你正在学习 Angular,那么你可能已经听说过独立组件(Component)。顾名思义,独立组件就是可以独立使用和管理的组件,它们能够被包含在其他组件中或被其他组件引用。 在本文中,我们…...
Lie group 专题:Lie 群
Lie group 专题:Lie 群 流形 流形的定义 一个m维流形是满足以下条件的集合M:存在可数多个称为坐标卡(图集)的子集合族.以及映到的连通开子集上的一对一映射,,称为局部坐标映射,满足以下条件 坐标卡覆盖M…...

Vue-打印组件页面
场景: 需要将页面的局部信息打印出来,只在前端实现,不要占用后端的资源。经过百度经验,决定使用 print-js和html2canvas组件。 1. 下载包 npm install print-js --save npm install --save html2canvas 2. 组件内引用 <script>impo…...

Python爬虫——scrapy_基本使用
安装scrapy pip install scrapy创建scrapy项目,需要在终端里创建 注意:项目的名字开头不能是数字,也不能包含中文 scrapy startproject 项目名称 示例: scrapy startproject scra_baidu_36创建好后的文件 3. 创建爬虫文件&…...

30 | 中国高校数据分析
一、数据源 本项目使用了两个csv的数据文件,一个是中国高校(大学)的数据,一个是中国高校专业设置的数据 数据基本栏位:高校(大学)的数据高校专业设置的数据学校学校省份专业类别城市专业名称地址国家特色专业水平层次办学类别办学类型985211双一流二、数据分析目标 本…...
开源低代码平台Openblocks
网友 HankMeng 想看低代码工具,正好手上有一个; 什么是 Openblocks ? Openblocks 是一个开发人员友好的开源低代码平台,可在几分钟内构建内部应用程序。 传统上,构建内部应用程序需要复杂的前端和后端交互,…...
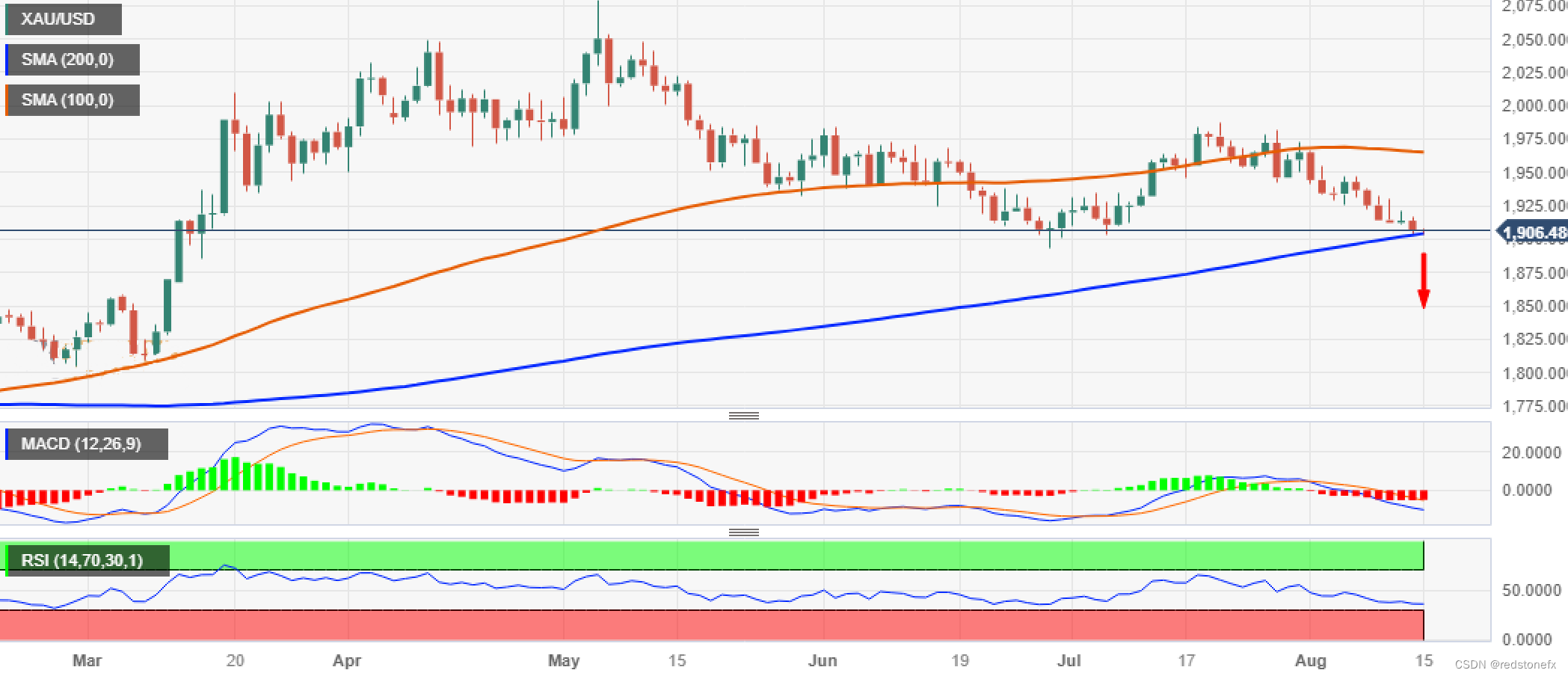
每日汇评:黄金在 200 日移动平均线附近似乎很脆弱,关注美国零售销售
1、金价预计将巩固其近期跌势,至 6 月初以来的最低水平; 2、对美联储再次加息的押注继续限制了贵金属的上涨; 3、金融市场现在期待美国零售销售报告带来一些有意义的推动; 周二金价难以获得任何有意义的牵引力,并在…...

DFT笔记 DC/AC mode与Func
DFT scan可以分为DC和AC两种,区别如下图 DC模式需要ate测试机台提供test clock时钟(最快100M),DFT工程师需要升级普通reg变成带si和so,se pin的reg,并插入扫描链(scan chain)&#x…...

docker核心操作
docker核心操作 1、docker安装(1)可选参数:(2)输出参数解释:2、docker镜像(1)拉取镜像:[https://www.docker.com/](https://www.docker.com/)3、运行docker镜像(1) 运行容器:(2) 挂载硬盘:4、docker容器的生命周期5.1、进入容器内部5.2、怎么解决Error: exec fai…...
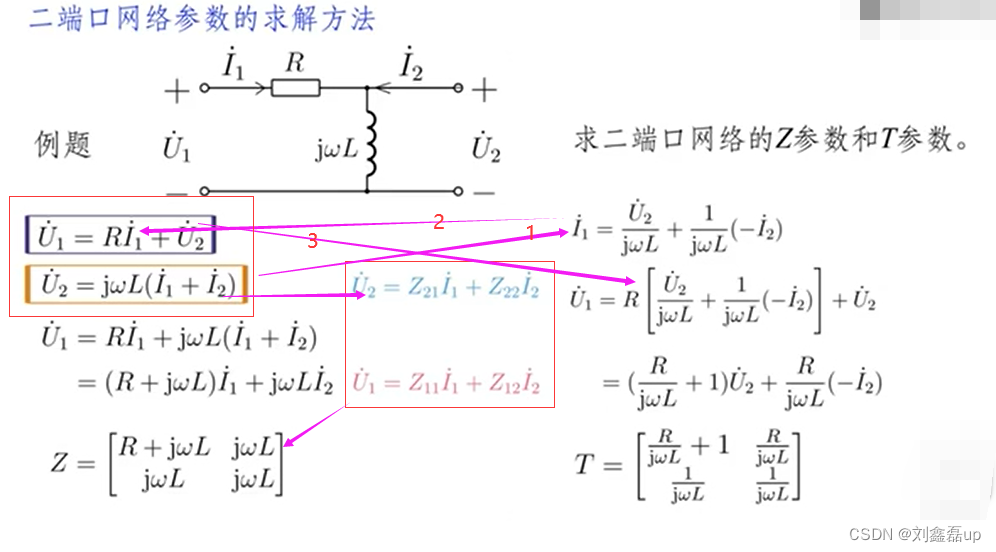
《电路》基础知识入门学习笔记
文章目录: 一:电路模型和电路规律 1.电路概述 2.电路模型 3.基本电路物理量:电流、电压、电功率和能量 4.电流和电压的参考方向 5.电路元件—电阻 6. 电路元件—电压源和电流源 7.受控电源 8.基尔霍夫(后面都要用这个方法…...

什么是P2P?
P2P (Peer-to-Peer) 是一种分布式的网络架构,其中各个节点(通常被称为“peers”或“节点”)直接进行数据共享和交换,而无需依赖中央服务器。P2P 网络强调平等的参与和共享,每个节点既可以是数据的消费者(下…...

matlab RANSAC拟合多项式曲线
目录 一、功能概述1、算法概述2、主要函数3、参考文献二、代码实现三、结果展示四、参考链接本文由CSDN点云侠原创,原文链接。爬虫网站自重,把自己当个人。爬些不完整的误导别人有意思吗???? 一、功能概述 1、算法概述 使用RANSAC对点进行多项式拟合。...

微信小程序nfc指令异常记录
小程序nfc相关代码: readEvent(){wx.getNFCAdapter().startDiscovery({success:(res)>{console.log(--------------start--------)console.log(res);wx.getNFCAdapter().onDiscovered(callback>{console.log(------------onDiscovered----------)console.log(callback)…...
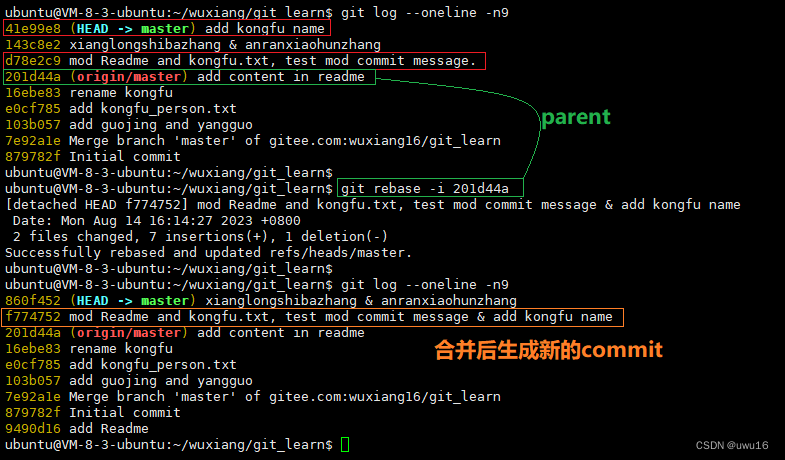
10 - 把间隔的几个commit整理成1个
查看所有文章链接:(更新中)GIT常用场景- 目录 文章目录 把间隔的几个commit整理成1个 把间隔的几个commit整理成1个...
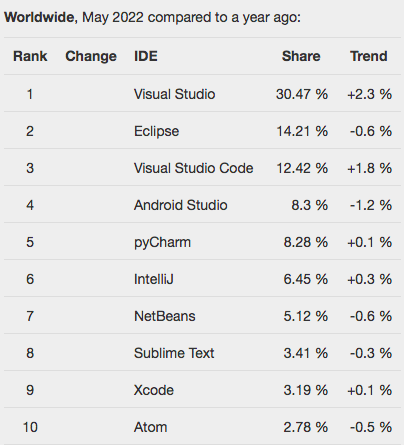
关于 Eclipse 的一场 “三角关系”
上个世纪 90 年代,世界上的计算机要么不联网,要么在企业内部联网。但是,在互联网的概念下,计算机之间共享信息和资源的需求成为了必要。 1995 年 5 月,Java 横空出世。Java 的父亲是当时凭借 Solaris 操作系统风头正盛…...

koa 使用 Mongoose 查询数据
Mongosee 操作符koa 使用 Mongoose 进行 翻页查询koa 使用 Mongoose 进行 多条件查询 mongosee 操作符 在使用 Koa 和 Mongoose 进行数据库查询时,你可以使用以下常用的操作符来构建查询条件: $eq:等于 示例:{ field: { $eq: valu…...
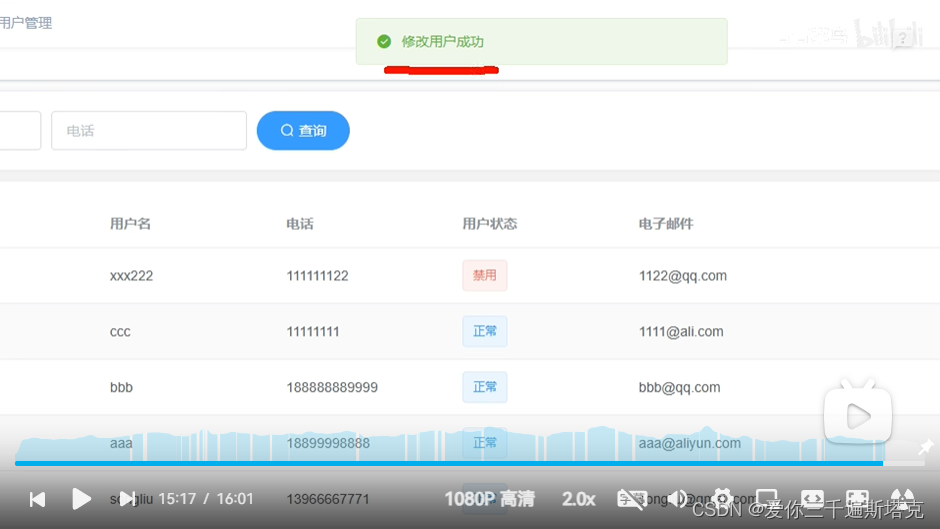
前后端分离------后端创建笔记(10)用户修改
本文章转载于【SpringBootVue】全网最简单但实用的前后端分离项目实战笔记 - 前端_大菜007的博客-CSDN博客 仅用于学习和讨论,如有侵权请联系 源码:https://gitee.com/green_vegetables/x-admin-project.git 素材:https://pan.baidu.com/s/…...
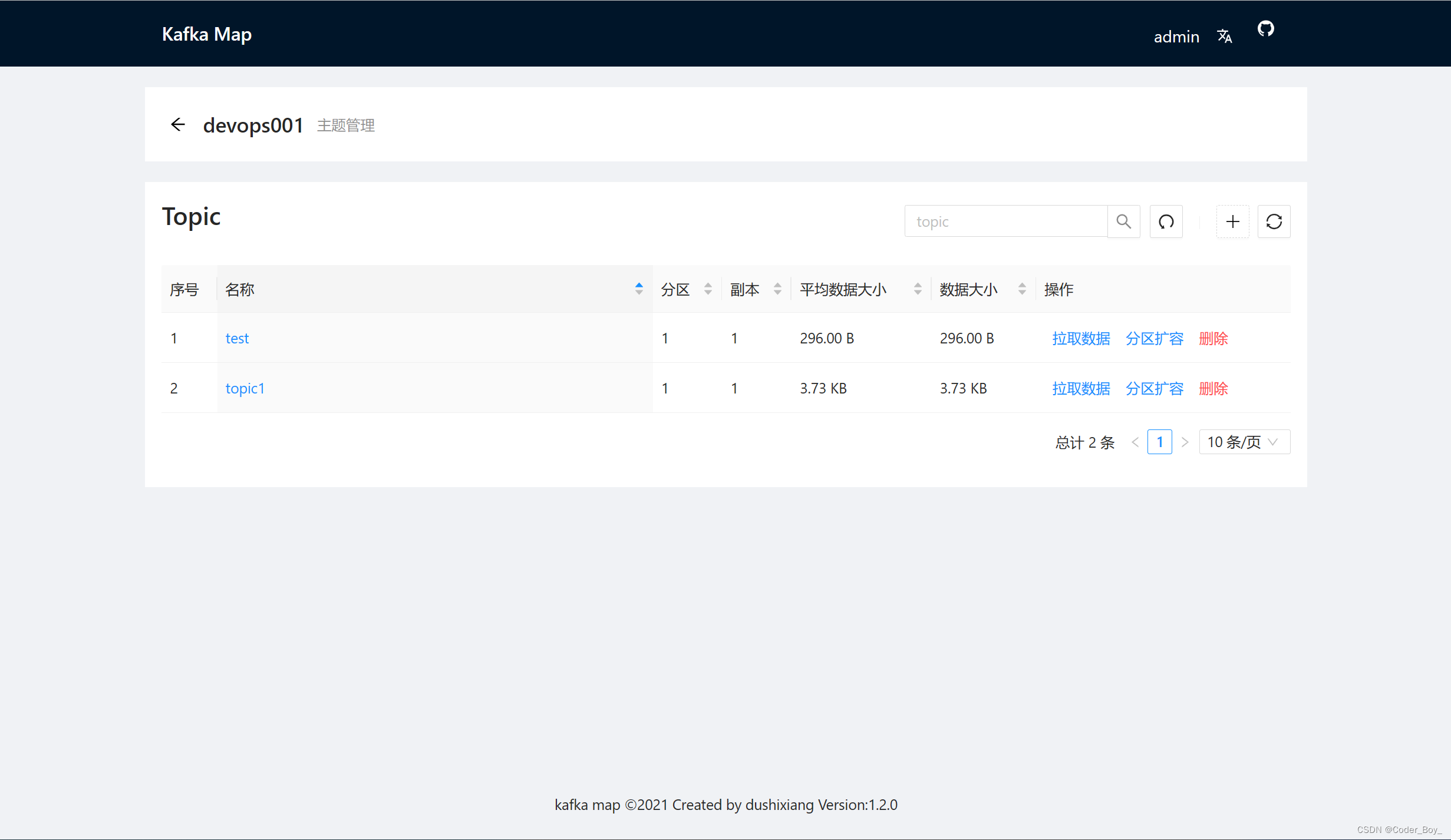
K8S系列文章之 Docker安装使用Kafka
通过Docker拉取镜像的方式进行安装 照例先去DockerHub找一下镜像源,看下官方提供的基本操作(大部分时候官方教程比网上的要清晰一些,并且大部分教程可能也是翻译的官方的操作步骤,所以直接看官方的就行) 老实说Kafka…...

js如何获取字符串大小是几M
js如何获取字符串大小是几M 在JavaScript中,可以使用以下方法来获取字符串的大小(以字节为单位): function getStringSizeInBytes(str) {// 使用UTF-8编码计算字符串的字节长度let totalBytes new Blob([str]).size;// 将字节长…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
