斐波那契数列(递归+迭代)
目录
- 什么是斐波那契数列
- 递归写法
- 使用递归写法的缺点
- 迭代写法(效率高)
什么是斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、3
通俗地来讲,斐波那契数列就是从第三位数字开始,每位的值是其前两位的和
递归写法
使用递归方法写十分简单
从第三位数字开始,每位的值是其前两位的和
- f(0) = 1
- f(1) = 1
- f(n) = f(n-1)+f(n-2)(n>3)
代码如下:
long long feibonahi(int n)
{if (n <= 2){return 1;}else{return feibonahi(n - 1) + feibonahi(n - 2);}
}
使用递归写法的缺点
我们分析一下递归算法的时间复杂度
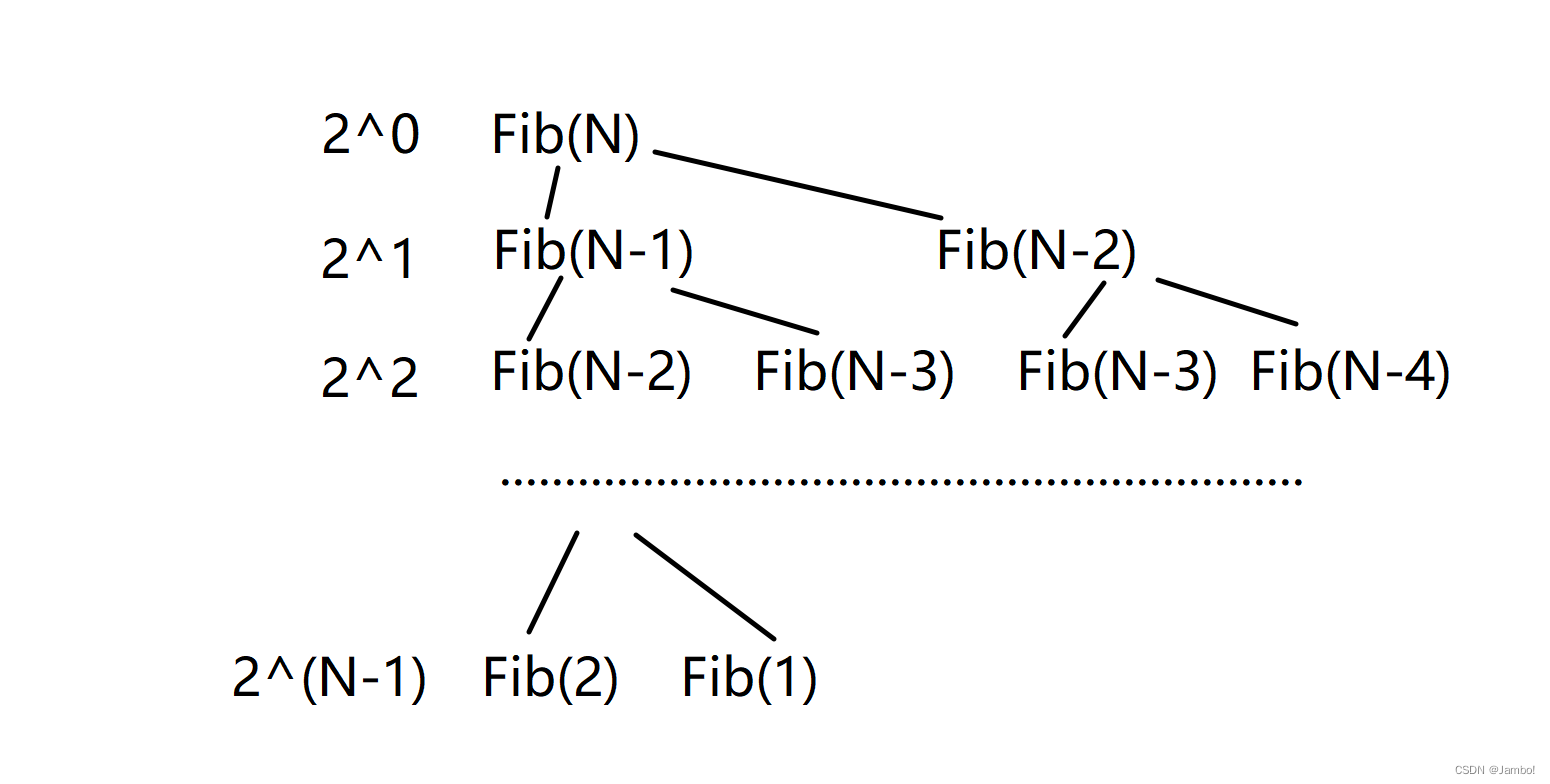
可以看出这个递归方法的时间复杂度是O(2^n)
可能这是没觉得时间复杂度是O(2^n)是多大的事,所以接下来我们计算一下传不同参数,这个递归算法的运行时间:
#include <stdio.h>
#include <time.h>long long Fib(int n)
{if (n <= 2){return 1;}else{return Fib(n - 1) + Fib(n - 2);}
}
int main()
{int begin1 = clock();Fib(10);int end1 = clock();int begin2 = clock();Fib(20);int end2 = clock();int begin3 = clock();Fib(30);int end3 = clock();int begin4 = clock();Fib(40);int end4 = clock();int begin5 = clock();Fib(50);int end5 = clock();printf("end1:%d\n", end1 - begin1);printf("end2:%d\n", end2 - begin2);printf("end3:%d\n", end2 - begin3);printf("end4:%d\n", end4 - begin4);printf("end5:%d\n", end5 - begin5);return 0;
}
下面我们可以看到:
从参数从10~40的运行时间还算快,然而将50传入函数中,可以看到,会运行一段时间

所以使用递归方法求斐波那契数列在理论上可行,但是在实际中是不可取的一个方法
另外,我们在这也看一下2^N的“威力”
- N==10,2^N = 1024
- N==20,2^N = 100万
- N==30,2^N = 10亿
- N==40,2^N = 1万亿
- N==50,2^N = 很大很大的数
所以我们不能使用递归算法,接下来我们写一个迭代方法
迭代写法(效率高)
int feibonahi2(int n)
{if (n == 1 || n == 2){return 1;}int a = 1;int b = 1;int c = 1;while (n > 2){c = a + b;a = b;b = c;n--;}return c;
}
这个算法的时间复杂度是O(N),上面的递归写法要好的太多太多
相关文章:

斐波那契数列(递归+迭代)
目录什么是斐波那契数列递归写法使用递归写法的缺点迭代写法(效率高)什么是斐波那契数列 斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardo Fibonacci)以兔子繁殖为例…...
2022黑马Redis跟学笔记.实战篇(六)
2022黑马Redis跟学笔记.实战篇 六4.7.达人探店功能4.7.1.分享探店图文1. 达人探店-发布探店笔记2. 达人探店-查看探店笔记4.7.2.点赞功能4.7.3.基于List实现点赞用户列表TOP104.7.4.基于SortedSet实现点赞排行榜4.8.关注列表4.8.1.关注列表实现原理4.8.2.添加关注1. 好友关注-关…...
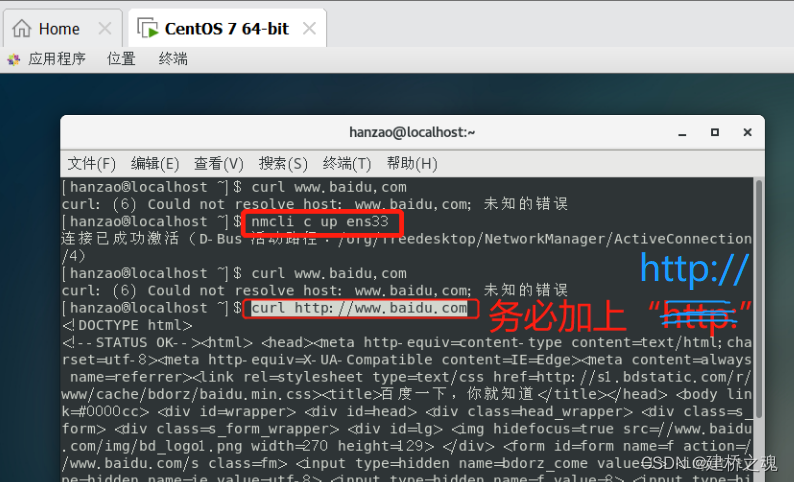
Linux-VMware常用设置(时间+网络)及网络连接激活失败解决方法-基础篇②
目录一、设置时间二、网络设置1. 激活网卡方法一:直接启动网卡(仅限当此)方法二:修改配置文件(永久)2. 将NAT模式改为桥接模式什么是是NAT模式?如何改为桥接模式?三、虚拟机网络连接…...

vue3学习总结1
一.vue3与vue2相比带来哪些变化?a.性能的提升(包括打包大小减少,初次渲染的速度加快,更新渲染速度加快,内存减少)b.源码的升级(响应式的原理发生了变化,由原来的defineProperty变成了…...
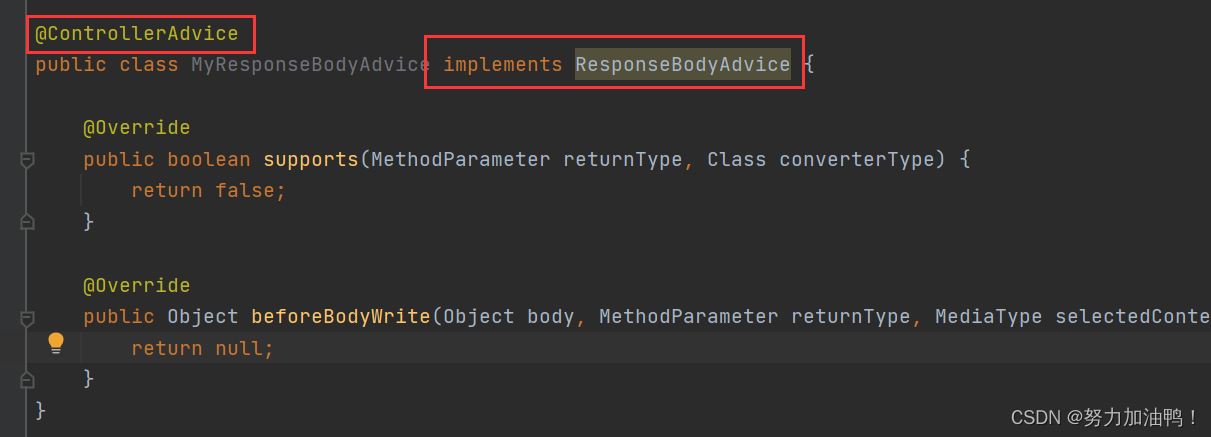
SpringBoot统一功能处理
一、统一用户登录权限验证 1.1Spring拦截器 实现拦截器需要以下两步: 1.创建自定义拦截器,实现 HandlerInterceptor 接⼝的 preHandle(执行具体方法之前的预处理)方法。 2.将⾃定义拦截器加⼊ WebMvcConfigurer 的 addIntercept…...
答案解析)
2022年3月电子学会Python等级考试试卷(五级)答案解析
目录 一、单选题(共25题,共50分) 二、判断题(共10题,共20分) 三、编程题(共3题,共30分) 青少年软件编程(Python)等级考试试卷(五级&#...

【C++】智能指针
目录 一、先来看一下什么是智能指针 二、 auto_ptr 1、C98版本 2、C11的auto_ptr 三、boost 库中的智能指针 1. scoped_ptr 2、shared_ptr(最好的智能指针) 四、C11中新提供的智能指针 unique_ptr shared_ptr std::shared_ptr的循环引用问题…...
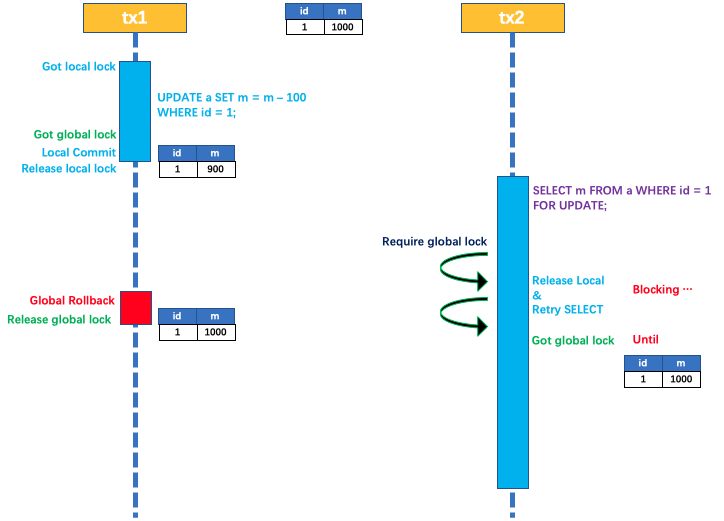
Seata架构篇 - AT模式
AT 模式 概述 Seata AT 模式是一种非侵入式的分布式事务解决方案,Seata 在内部做了对数据库操作的代理层,我们使用 Seata AT 模式时,实际上用的是 Seata 自带的数据源代理 DataSourceProxy,Seata 在这层代理中加入了很多逻辑&am…...
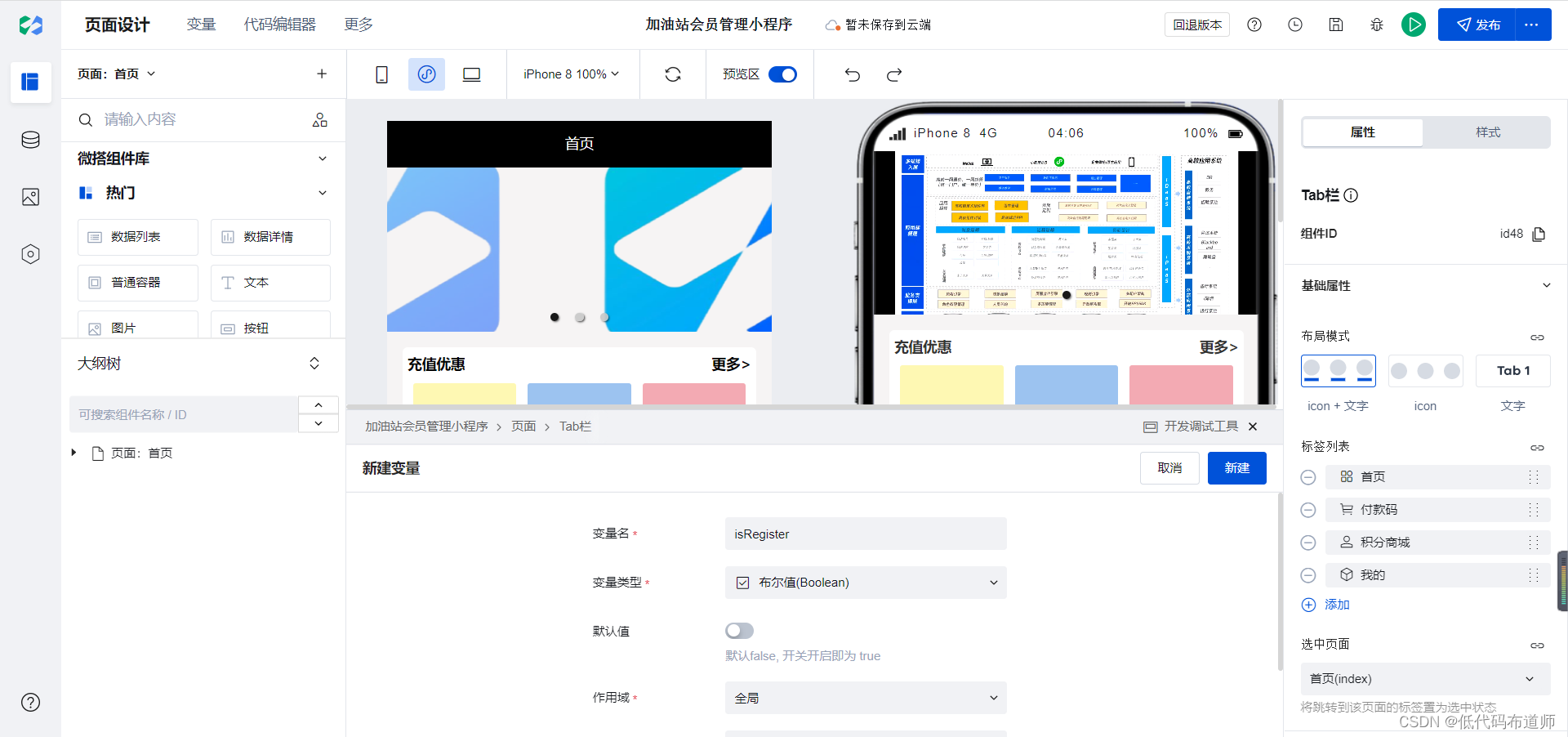
加油站会员管理小程序实战开发教程12
我们上一篇介绍了会员数据源的开发,本节我们介绍一下会员注册功能。 首先呢梳理一下会员注册的业务逻辑,如果用户是首次登录,那他肯定还没有给我们的小程序提交任何的信息。那么我们就在我的页面给他显示一个注册的按钮,如果他已经注册过了,那么就正常显示会员的信息,他…...
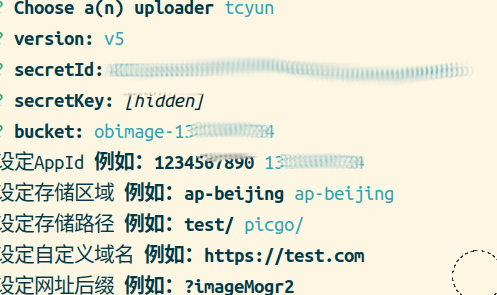
用腾讯云同步Obsidian笔记
介绍 之前用gitee同步OB笔记,同时做图床。但由于git系产品设置起来相对复杂,且后续可能有外链过审等问题。周五被同事小姐姐安利了用腾讯云COS,试了一下,果然不错。其主要优点如下: 设置简单,学习成本低&…...
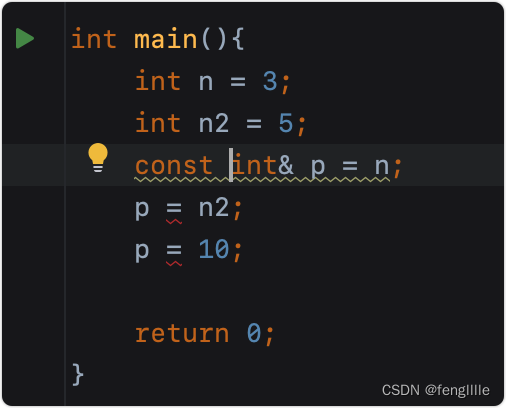
浅析C++指针与引用,栈传递的关系
目录 前言 C 堆指针 栈指针 常量指针 指针常量 引用 常量引用 总结 前言 目前做了很多项目,接触到各种语言,基本上用什么学什么,语言的边际就会很模糊,实际上语言的设计大同小异,只是语言具备各自的特性区别。…...

图解LeetCode——剑指 Offer 10- II. 青蛙跳台阶问题
一、题目 一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。 答案需要取模 1e97(1000000007),如计算初始结果为:1000000008,请返回 1。 二、示例 2.1>…...

【Linux】用户分类+权限管理+umask+粘滞位说明
目录 1.用户分类 su指令 2.认识Linux权限 2.1 文件访问者的分类 2.2 文件类型和访问权限 a. 文件类型 file指令 b. 访问权限 2.3 文件权值的表示方法 a. 字母表示法 b. 八进制表示法 3.如何修改文件访问者的权限及相关指令 1. chmod指令 2. chown指令 3. chgrp指…...
【干货】如何打造HR无法拒绝的简历?测试开发大牛带手把手你写简历!
通过率90%,优秀的软件测试简历长什么样? 也许口才好的人会觉得简历不重要,能说就行了,那是因为你没有体会过石沉大海的感觉! 很多人觉得疑惑,为什么我投了那么多简历,都没有接到面试通知&…...
nodejs学习-4:nodejs连接mongodb和相关操作
1. express生成器生成express模板 前提需要首先下载好:express-generator,命令如下(全局安装) npm install -g express-generator生成模板命令如下: express 项目名称 --viewejs // --view 参数表示前端界面使用的引擎,这里使用…...

【博客629】Linux DNS解析原理与配置
Linux DNS解析原理与配置 1、DNS缓存 作用: 程序客户端、下游的 DNS 服务器每次查询 DNS 成功之后,通常会将该 DNS 记录缓存一段时间,避免频繁发出查询请求的耗时。 Linux下的DNS缓存: Linux 系统默认不会在本地建立 DNS 缓存…...

【CSP】202212-2 训练计划
题目 问题背景 西西艾弗岛荒野求生大赛还有 天开幕! 问题描述 为了在大赛中取得好成绩,顿顿准备在 天时间内完成“短跑”、“高中物理”以及“核裂变技术”等总共 项科目的加强训练。其中第 项( )科目编号为 ,也可简…...
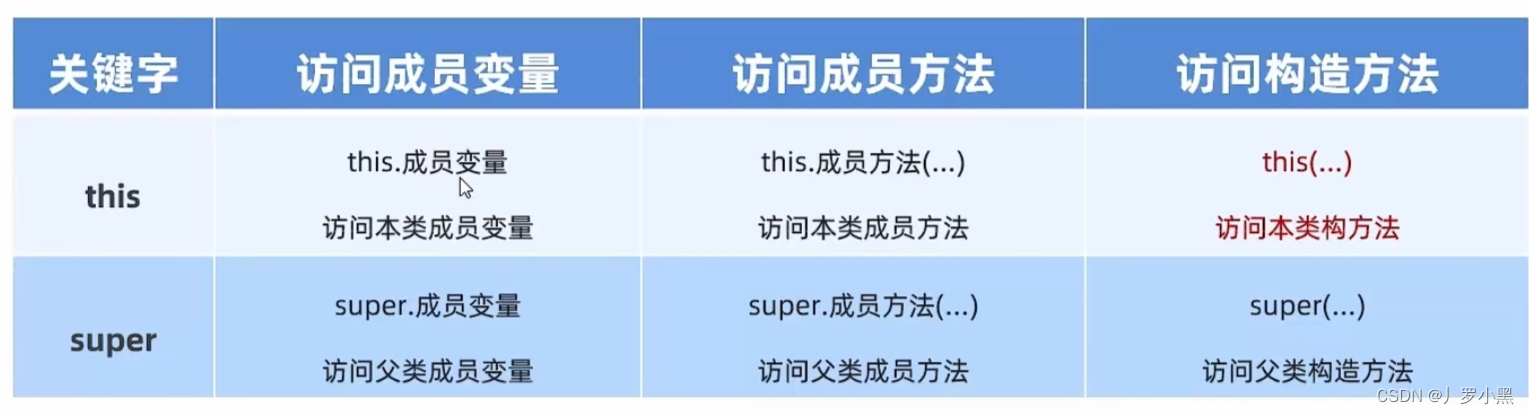
java基础学习 day42(继承中构造方法的访问特点,this、super的使用总结)
继承中,构造方法的访问特点 父类的构造方法不会被子类继承,但可以通过super()调用父类的构造方法,且只能在子类调用,在测试类中是不能手动单写构造方法的。子类中所有的构造方法默认先调用父类的无参构造,再执行自己构…...

生物医药多组学与生物信息方法介绍
基因组学告诉你可能发生什么,转录组学和蛋白组学告诉你即将发生什么,而代谢组学告诉你正在发生什么 1、多组学与生信方法 生物医学技术的组学包括基因组学、转录组学、蛋白质组学、代谢组学和表观基因组学等。这些组学研究领域通过大量数据的高通量技术…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

