视觉slam十四讲---第一弹三维空间刚体运动
1.旋转矩阵
1.1内积

1.2外积

1.3坐标系间的欧式变换
相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会 发生变化。这种变换称为欧氏变换。
旋转矩阵:它是一个行列式为 1 的正交矩阵。

旋转矩阵为正交阵,它的逆(即转置)描述了一个相反的旋转。
加上平移:

1.4变换矩阵与齐次坐标

关于变换矩阵 T,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左 下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧氏群(Special Euclidean Group):
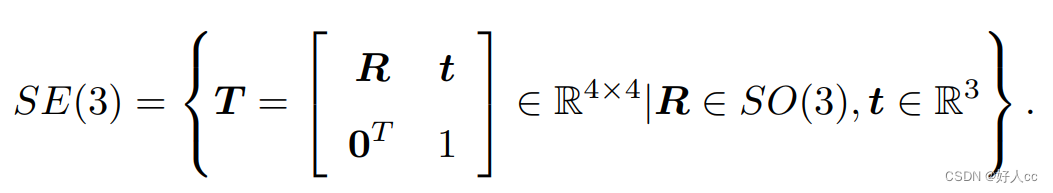
求解该矩阵的逆表示一个反向的变换:
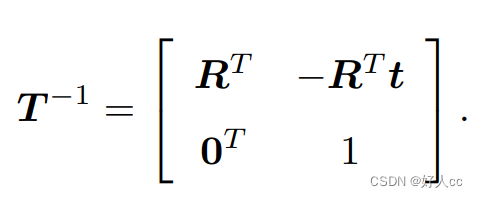
2.Eigen库---线性代数库
#include <Eigen/Core> //核心部分
#include <Eigen/Dense> //稠密矩阵的代数运算(逆、特征值等)
using namespace Eigen;
//所有的向量,矩阵都是
Matrix<数据类型,行,列>
Vector3d实质是 Matrix<double,3,1>
可以直接求逆 QR分解 cholesky分解Eigen对数据类型转换严格,可以通过显示转换来完成转换。
3.旋转向量和欧拉角
3.1旋转向量
事实上, 任意旋转都可以用一个旋转轴和一个旋转角来刻画。
于是,我们可以使用一个 向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量(或轴角,AxisAngle)。这种表示法只需一个三维向量即可描述旋转。同样,对于变换矩阵,我们使用一 个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。
旋转向量和旋转矩阵 之间是如何转换的呢?假设有一个旋转轴为 n,角度为 θ 的旋转,显然,它对应的旋转向 量为 θn。由旋转向量到旋转矩阵的过程由罗德里格斯公式
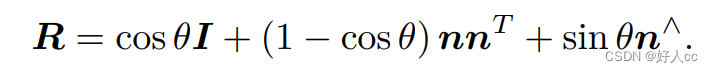
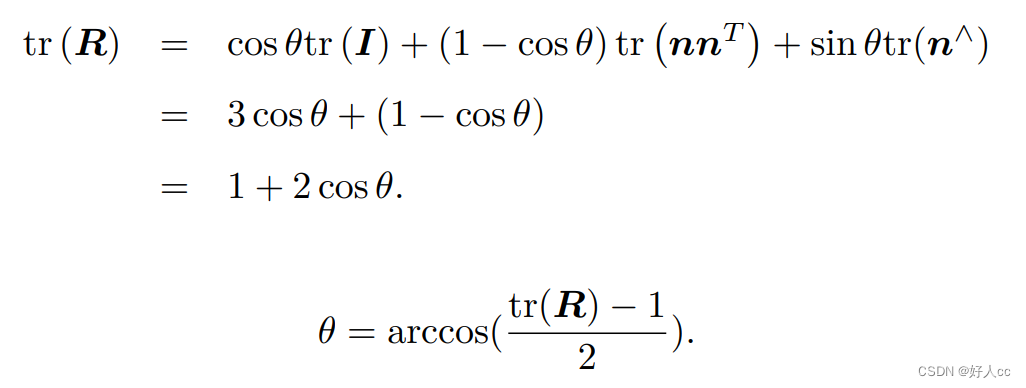

3.2欧拉角

欧拉角的一个重大缺点是会碰到著名的万向锁问题(Gimbal Lock①):在俯仰角为 ±90◦ 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由三次 旋转变成了两次旋转)。这被称为奇异性问题,在其他形式的欧拉角中也同样存在。
4.四元数
既是紧凑的,也没有奇异性。如果说缺点的话,四元数不够直观,其运算稍为复杂一些。



这式子给我们一种微妙的“转了一半”的感觉。同样,对式(3.19)的 θ 加上 2π,我们得到一个相同的旋转,但此时对应的四元数变成了 −q。因此,在四元数中,任意的旋转都可以由两个互为相反数的四元数表示。
四元数和自己的逆的乘积为实四元数的 1:

5.四元数到旋转矩阵的转换

6.变换性质
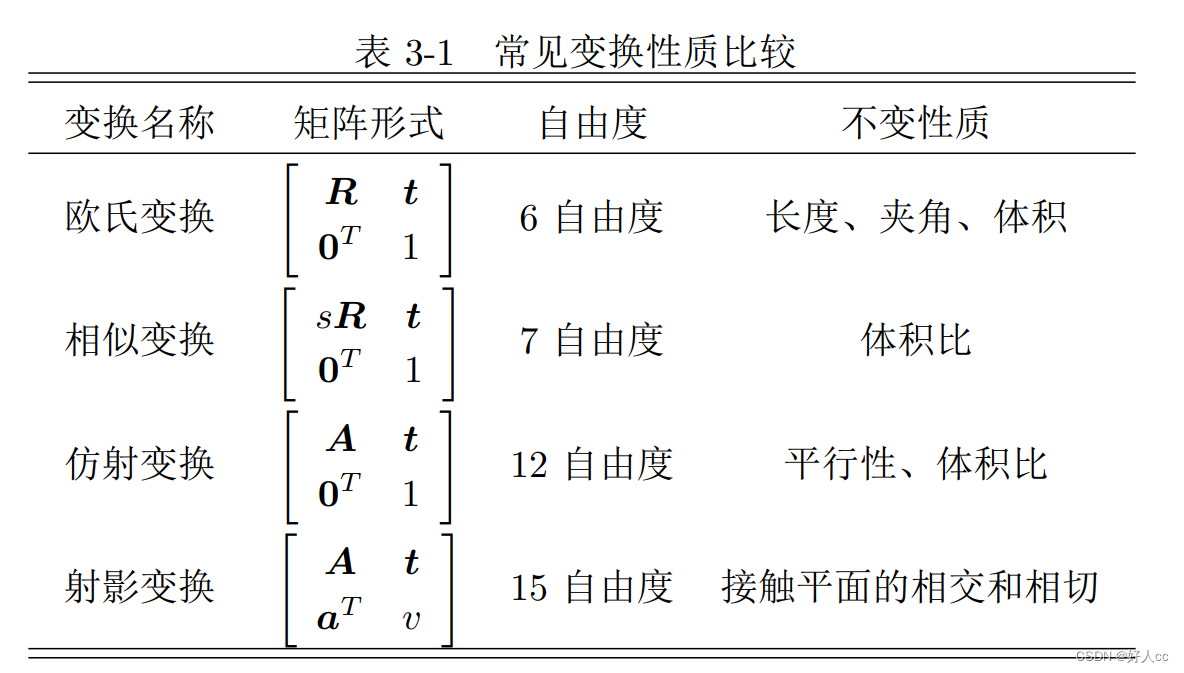
相关文章:

视觉slam十四讲---第一弹三维空间刚体运动
1.旋转矩阵 1.1内积 1.2外积 1.3坐标系间的欧式变换 相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会 发生变化。这种变换称为欧氏变换。 旋转矩阵:它是一个行列式为 1 的正交矩阵。 旋转矩阵为正交阵,它的逆…...
手把手教你配置Jenkins自动化邮件通知
完成基于Jenkins的持续集成部署后,自动化测试执行后,测试结果需要通知到相关人员,除了钉钉通知外我们还可以通过Email通知到对应负责人,这里记录一下测试结果通过Jenkins邮件通知的配置与部署 01、安装插件 方法1: 进…...

Arcgis连续数据的分类(求不同值域的面积)
问题描述:如果得到的一个连续的影响数值数据,但是我们想求取某一段值域的面积占比,需要进行以下操作: 1.按照数值重分类,将某段数值变成一个类别 2.栅格转矢量,再求取面积...

C++ 函数
函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定的,但在逻辑上,划分通常…...

关于如何创建一个windows窗口的exe文件
如何创建一个windows窗口exe文件,具体参照这个博主: http://t.csdn.cn/pfQK5 以下是实现代码,注意用vs打开: #pragma comment( linker, "/subsystem:\"windows\" /entry:\"WinMainCRTStartup\"" …...
re学习(33)攻防世界-secret-galaxy-300(动态调试)
下载压缩包: 下载链接:https://adworld.xctf.org.cn/challenges/list 参考文章:攻防世界逆向高手题之secret-galaxy-300_沐一 林的博客-CSDN博客 发现这只是三个同一类型文件的三个不同版本而已,一个windows32位exe࿰…...
springboot工程集成前端编译包,用于uni-app webView工程,解决其需独立部署带来的麻烦,场景如页面->画布->图片->pdf
前端工程 访问方式 http://127.0.0.1:8080/context/frontEnd/index放行 public class SecurityConfig extends WebSecurityConfigurerAdapter { "/frontEnd/**",SysFrontEndController import lombok.extern.slf4j.Slf4j; import nl.basjes.shaded.org.springfram…...
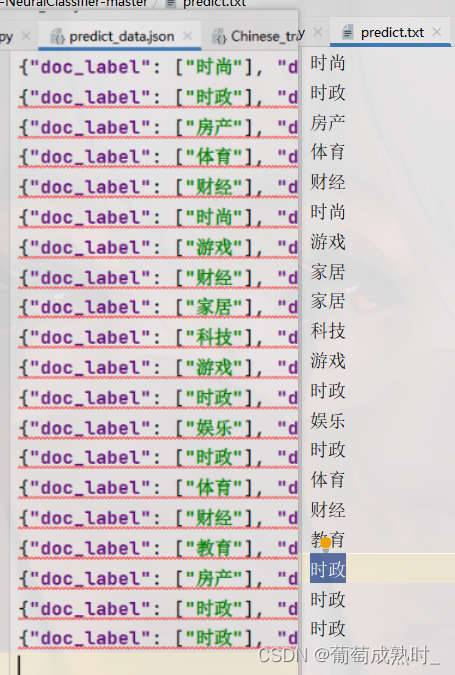
NeuralNLP-NeuralClassifier的使用记录(二),训练预测自己的【中文文本多分类】
NeuralNLP-NeuralClassifier的使用记录,训练预测自己的【中文文本多分类】 数据准备: 与英文的训练预测一致,都使用相同的数据格式,将数据通过代码处理为JSON格式,以下是我使用的一种,不同的原数据情况…...

express学习笔记8 - 文件上传 下载以及预览
一、上传 1、 安装multer (任意选其中一种) yarn add multer --S npm install multer --S 2、新建配置文件(utils/multerConfig) const multer require(multer); const mkdirp require(mkdirp); // const sd require(silly-datetime); const path require(path);con…...
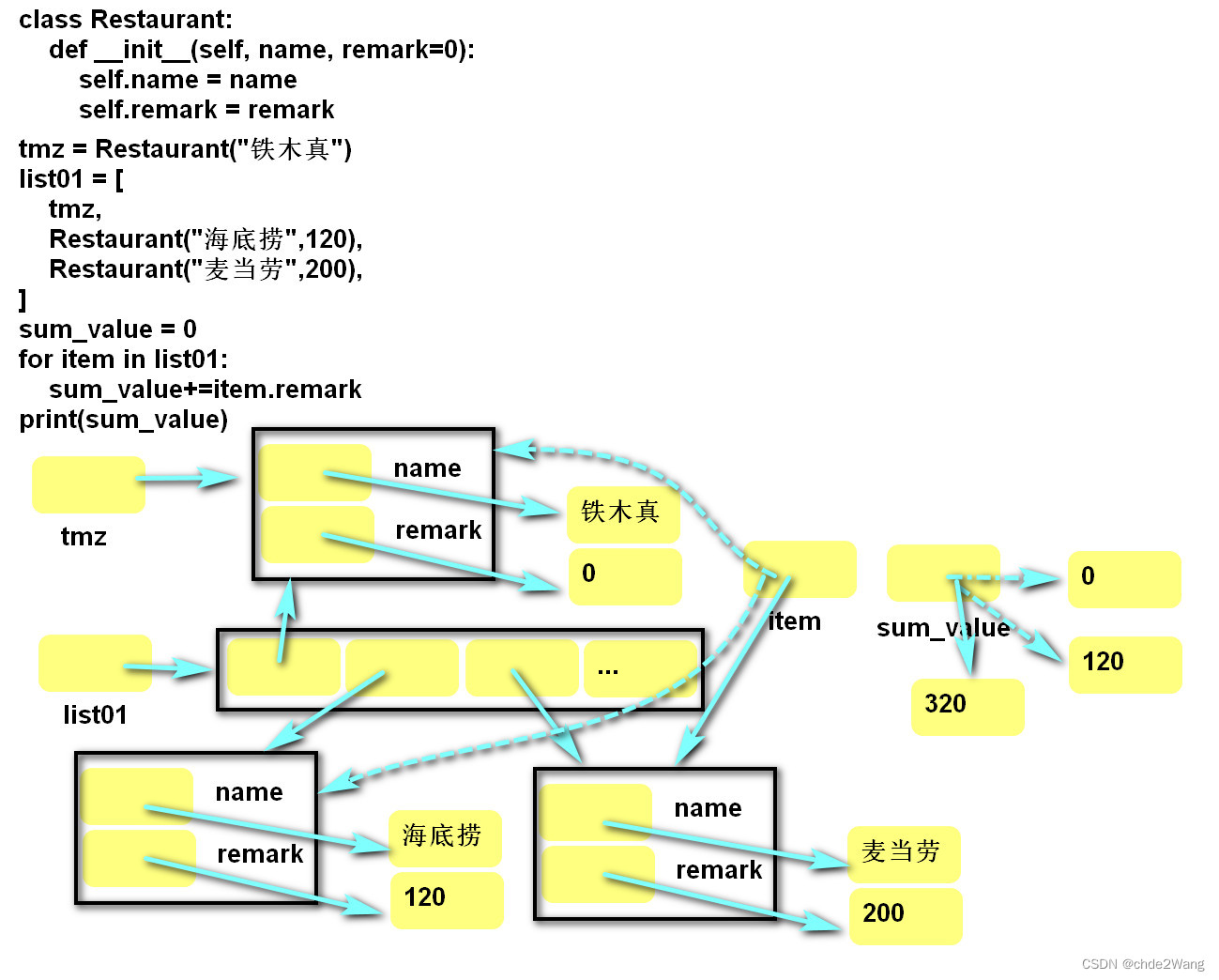
Python系统学习1-9-类(一)
一、类之初印象 1、类就是空表格,将变量(列名)和函数(行为)结合起来 2、创建对象,表达具体行 3、创建类就是创建数据的模板 --操作数据时有提示 --还能再组合数据的行为 --结构更加清晰 4、类的内存分配…...
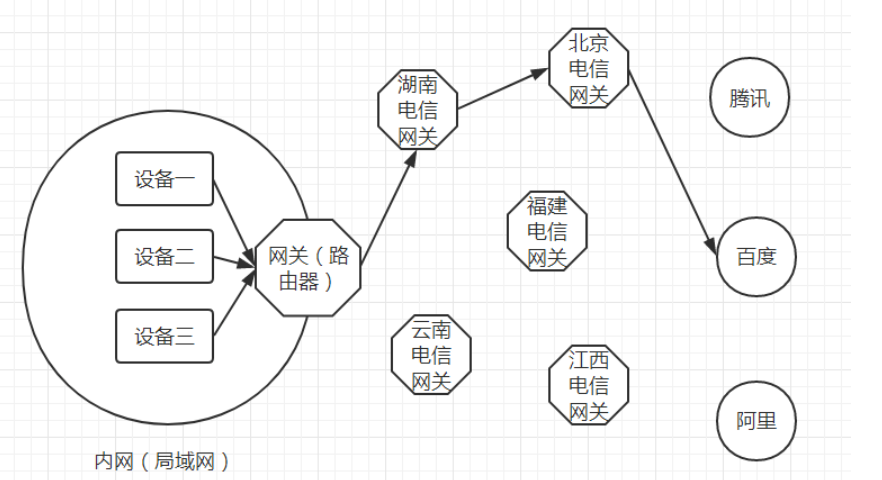
什么是公网、私网、内网、外网?
中午好,我的网工朋友。 最近经常有很多小白朋友在问,公网、私网、内网、外网,这些的概念是啥样的,又该怎么去界定。 关于IP地址,确实没有太明确的区分,其实也不必太过咬文嚼字。 内网、外网就是一个参考…...
一篇文章教会你搭建私人kindle图书馆,并内网穿透实现公网访问
搭建私人kindle图书馆,并内网穿透实现公网访问 在电子书风靡的时期,大部分人都购买了一本电子书,虽然这本电子书更多的时候是被搁置在储物架上吃灰,或者成为盖泡面的神器,但当亚马逊发布消息将放弃电子书在中国的服务…...
好用的安卓手机投屏到mac分享
工具推荐:scrcpy github地址:https://github.com/Genymobile/scrcpy/tree/master mac使用方式 安装环境,打开terminal,执行以下命令,没有brew的先安装brew brew install scrcpy brew install android-platform-too…...
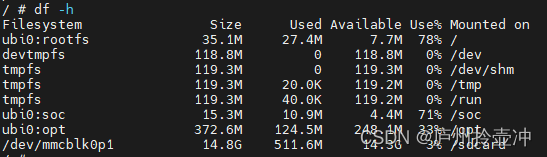
df -h
df -h 命令用于查看磁盘占用的空间 Filesystem:表示该文件系统位于哪个分区,因此该列显示的是设备名称; Used:表示用掉的磁盘空间大小; Available:表示剩余的磁盘空间大小; Use%:磁盘…...
彻底卸载Android Studio
永恒的爱是永远恪守最初的诺言。 在安装Android Studio会有很多问题导致无法正常运行,多次下载AS多次错误后了解到,删除以下四个文件才能彻底卸载Android Studio。 第一个文件:.gradle 路径:C:\Users\yao(这里yao是本…...

QT 5.12配置OpenCV3.4.10
主要过程:使用cmake编译源码,生成Mingw64位 下的OpenCV库 三篇博客解决问题: 1.Windows下安装Qt并使用cmake配置opencv3.4.10(含错误记录及解决办法)_d:\qt\qt5.14.2\5.14.2\mingw73_64\include\qtcore\qg_会飞的DA象的博客-CSDN博客 2.【…...

Qt应用开发(基础篇)——选项卡窗口 QTabWidget
一、前言 QTabWidget类继承于QWidget,是一个拥有选项卡的窗口部件。 QTabWidget类有一个选项卡栏QTabBar和一个页面区域,用来显示和选项卡相关联的界面。用户通过点击选项卡或者自定义快捷方式(ALTKey)切换页面。 二、QTabWidget类 1、count 该属…...

Socks5代理在多线程爬虫中的应用
在进行爬虫开发过程中,我们常常需要处理大量的数据,并执行多任务并发操作。然而,频繁的请求可能会引起目标网站的反爬机制,导致IP封禁或限制访问。为了规避这些限制,我们可以借助Socks5代理的强大功能,通过…...
初探)
机器学习笔记:主动学习(Active Learning)初探
1 基本介绍 监督学习问题中,存在标记成本昂贵且难以大量获取的问题。 针对一些特定任务,只有行业专家才能为样本做上准确标记。在此问题背景下,主动学习(Active Learning, AL)尝试通过选择性地标记较少数据而训练出表…...

linux github 仓库管理常用操作
linux 的常用操作 linux 本地 ssh验证连接github账号本地仓库连接远程私有仓库push/pull操作 Connecting to Github with ssh git local configuration If you are using git for the first time, configure the user name and email in the device. git config --global u…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
