chapter 3 Free electrons in solid - 3.1 自由电子模型
3.1 自由电子模型 Free electron model

研究晶体中的电子:
- 自由电子理论:不考虑离子实
- 能带理论:考虑离子实(周期性势场)的作用
3.1.1 德鲁德模型 Drude Model - Classical Free Electron Model
(1)德鲁德模型
德鲁德模型:价电子游离于特定原子周围,弥散于整个晶体中,形成“自由电子气”。
The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials (especially metals). The model, which is an application of kinetic theory, assumes that the microscopic behavior of electrons in a solid may be treated classically and looks much like a pinball machine, with a sea of constantly jittering electrons bouncing and re-bouncing off heavier, relatively immobile positive ions.
Assumption of the electron gas:
- 独立电子近似 Independent electron approximation: No electrostatic interaction and collision among free electrons(自由电子之间没有相互作用和碰撞)
- 自由电子近似 Free electron approximation: No electrostatic interaction between free electrons and ions(电子和离子实之间只有碰撞,没有静电相互作用)
- 碰撞假设 Collision assumption: Velocity of electrons after collision with ions only concerns with temperature, but not the velocity before collision(电子和离子实的碰撞是瞬时的,碰撞后的速度仅与温度有关)
- 弛豫时间近似 Relaxation time approximation: Relaxation time τ is independent with the position and velocity of electrons(弛豫时间即同一粒子两次碰撞的时间间隔,它仅依赖于晶体结构)
在德鲁德模型中,存在电场时,电子每两次碰撞之间都会获得电场加速,从而形成漂移速度 v d v_d vd,且漂移速度远小于电子热运动的速度 v d ≪ v R M S = 3 k B T m v_d \ll v_{RMS} = \sqrt{\frac{3k_BT}{m}} vd≪vRMS=m3kBT
利用德鲁德模型能够成功解释:
- 欧姆定律
- Wiedemann-Franz ratio comes out close to right for most materials
- Many other transport properties predicted correctly


(2) failure of Drude Model
德鲁德模型存在的问题:
- 电子比热 Specific Heat of electrons
- 电导率与温度的关系 Temperature dependence of σ
- Wiedemann-Franz ratio
- The Seebeck/Peltier coefficient come out wrong by a factor of 100.
Despite the shortcomings of Drude theory, it nonetheless was the only theory of metallic conductivity for a quarter of a century (until the Sommerfeld theory improved it), and it remains quite useful today.
3.1.2 索末菲模型 Sommerfeld Model - Quantum Mechanical Free Electron Model
索末菲保留了德鲁德的自由电子气假设(前两个),但是索末菲去除了“碰撞”的概念,引入量子统计的理论(费米-狄拉克分布 Fermi-Dirac Distribution)。
(1)势阱 potential well
1D Infinite Potential Well
( − ℏ 2 2 m d 2 d x 2 + U ( x ) ) ψ ( x ) = E ψ ( x ) \left( -\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + U(x) \right ) \psi (x) = E \psi(x) (−2mℏ2dx2d2+U(x))ψ(x)=Eψ(x)
k = n π L , n = 1 , 2 , 3 , … k = n \frac{\pi}{L}, \ \ n=1,2,3,\dots k=nLπ, n=1,2,3,…
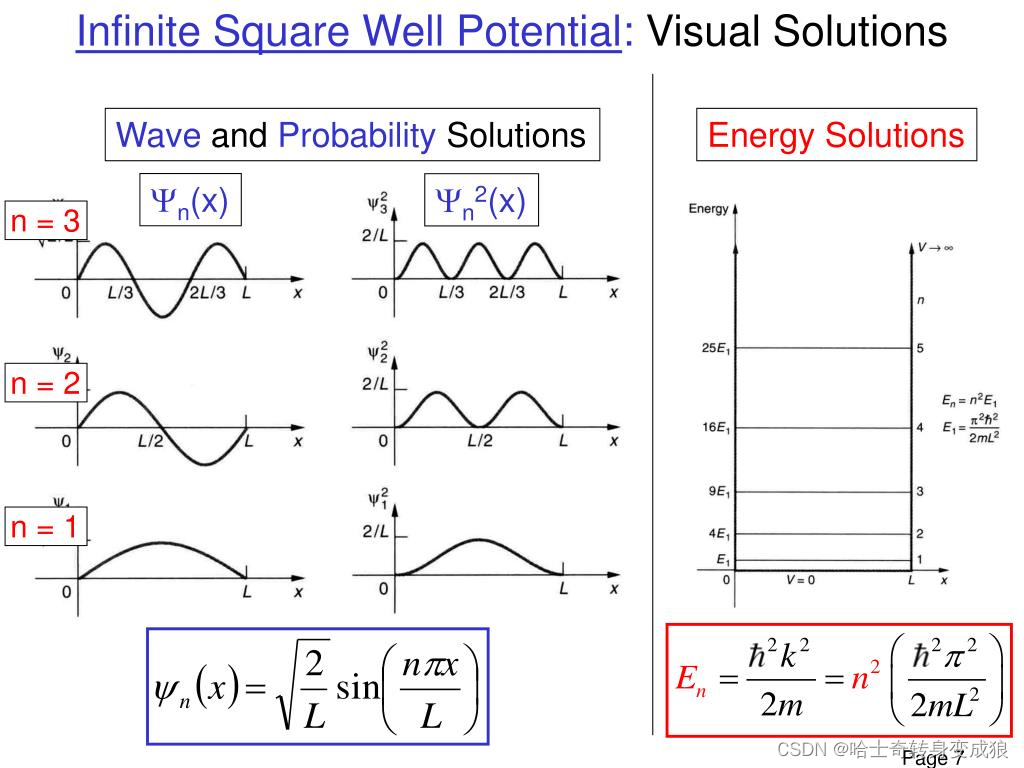
3D Infinite Potential Well

− ℏ 2 2 m ( ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 ) ψ ( x , y , z ) = E ψ ( x , y , z ) -\frac{\hbar ^2}{2m}\left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right) \psi(x,y,z) = E \psi (x,y,z) −2mℏ2(∂x2∂2+∂y2∂2+∂z2∂2)ψ(x,y,z)=Eψ(x,y,z)
ψ ( x , y , z ) = ψ ( x ) ψ ( y ) ψ ( z ) \psi(x,y,z) = \psi(x) \psi(y) \psi(z) ψ(x,y,z)=ψ(x)ψ(y)ψ(z)
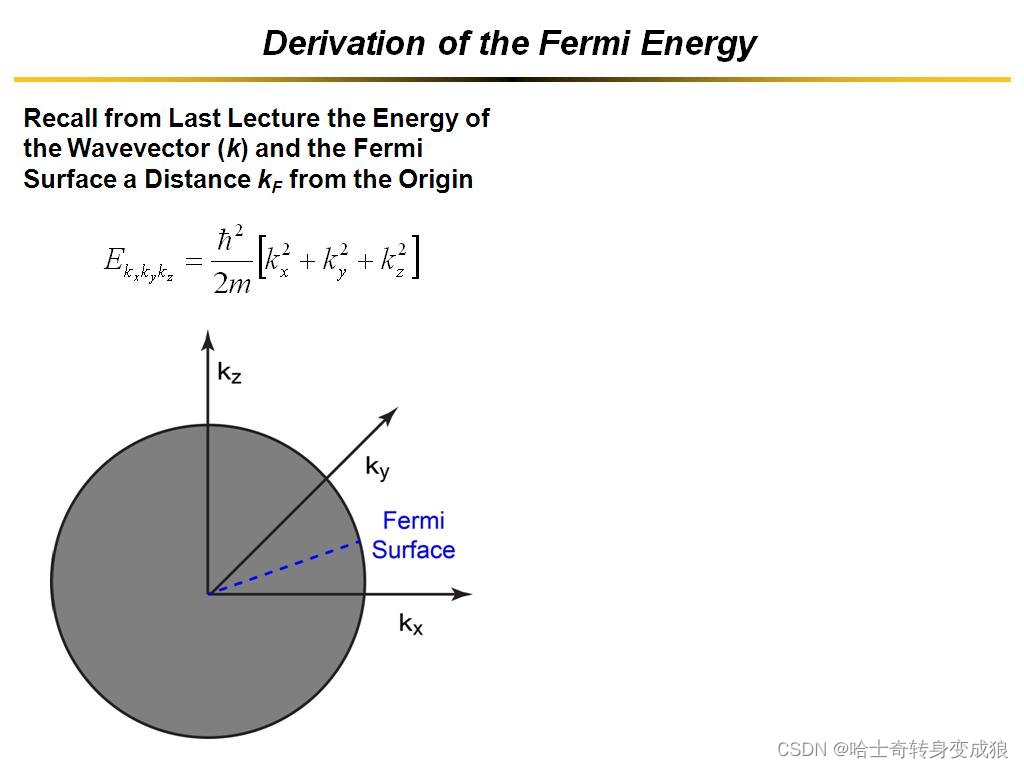
∵ E = ℏ 2 k 2 2 m , k ⃗ = k x i ⃗ + k y j ⃗ + k z l ⃗ \because E = \frac{\hbar ^2 k^2}{2m}, \ \ \vec k = k_x \vec i + k_y \vec j + k_z \vec l ∵E=2mℏ2k2, k=kxi+kyj+kzl
∴ E = ℏ 2 2 m ( k x 2 + k y 2 + k z 2 ) \therefore E = \frac{\hbar^2}{2m} (k_x^2 + k_y^2 + k_z^2) ∴E=2mℏ2(kx2+ky2+kz2)

(2)费米-狄拉克分布与费米能 Fermi-Dirac distribution & Fermi Energy
F l = α l ω l = 1 e ( α + β E l ) + 1 = 1 e ( E l − μ ) / k B T + 1 = 1 e ( E l − E F ) / k B T + 1 F_l = \frac{\alpha _l}{\omega _ l} = \frac{1}{e^{(\alpha + \beta E_l)} + 1} = \frac{1}{e^{(E_l - \mu)/k_B T} + 1} = \frac{1}{e^{(E_l - E_F)/k_B T} + 1} Fl=ωlαl=e(α+βEl)+11=e(El−μ)/kBT+11=e(El−EF)/kBT+11
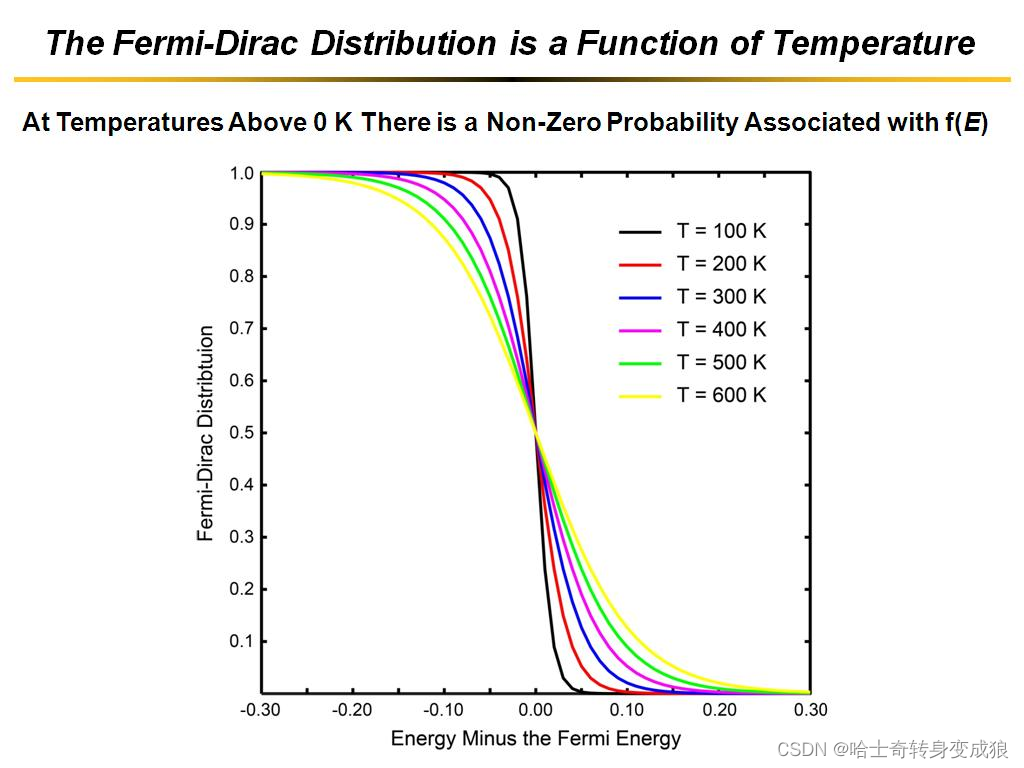
a. Classical theory of Occupancy Condition at T=0K
- 电子能量可以相同,不同电子可以占据同一能级,即不同电子具有相同的量子态。
- 电子分布满足Maxwell-Boltzmann分布。
- 一个系统的温度反应了系统内粒子运动的动能,T=0,所有电子静止不动。 1 2 m v ˉ 2 = 3 2 k B T , ∴ T = 0 K , v = 0 \frac{1}{2} m \bar v^2 = \frac{3}{2}k_B T,\ \ \ \therefore T=0K,\ v=0 21mvˉ2=23kBT, ∴T=0K, v=0
b. Quantum mechanically of Occupancy Condition at T=0K
Pauli’s Exclusion Principle:两个费米子不能处于同一量子态。
考虑自旋,一个能级对应有f组量子数,即有f重简并,这一个能级可以放2f个电子。
费米能级:在绝对零度时,一个费米子具有的最高能量。
The Fermi energy : the highest energy a fermion can take at absolute zero temperature.
假想把所有的费米子从量子态上移开,之后再把这些费米子按照一定的规则填充在各个可供占据的能量态上,并且这种填充过程中每个费米子都占据最低的可供占据的量子态。最后一个费米子占据的量子态即可粗略地认为是费米能级。
c. Quantum mechanically of Occupancy Condition at T>0K
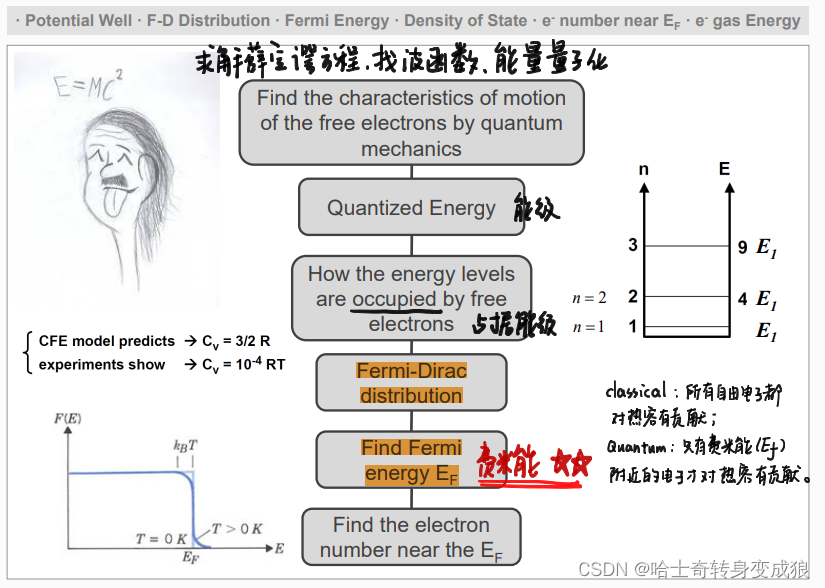
CFE model predicts: C V = 3 2 R C_V=\frac{3}{2}R CV=23R
experiments show: C V = 1 0 − 4 R T C_V = 10^{-4} RT CV=10−4RT
经典自由电子模型认为,所有电子都会对热容有贡献;量子力学认为,只有费米能级附近的电子才有可能脱离原子,具有导电特性,因为高能级被占据导致低能级电子无法跃迁。
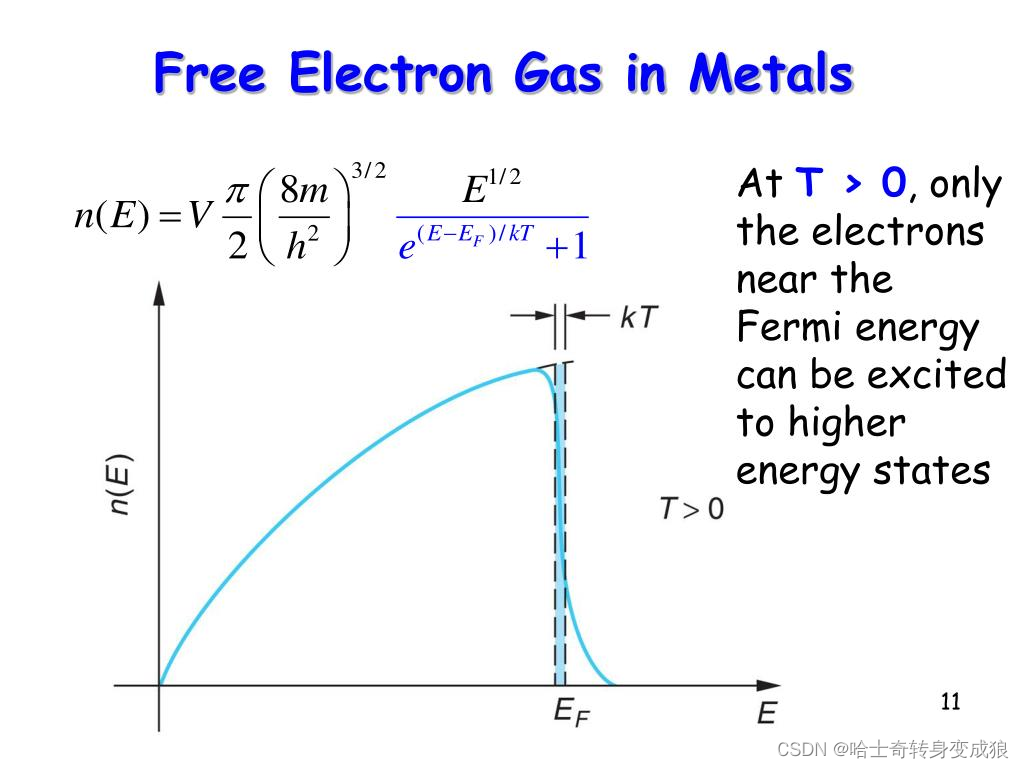
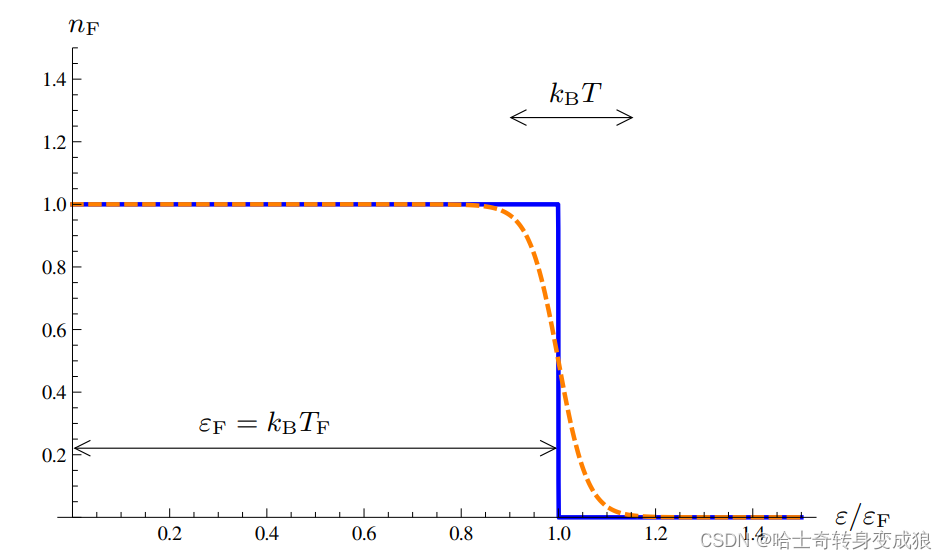
The Fermi–Dirac distribution at zero temperature (solid line) constitutes a step function. For T > 0 (dashed line), broadening appears in a region of width k B T k_B T kBT around the Fermi edge located at ε = ε F = k B T F . ε = ε_F = k_B T_F. ε=εF=kBTF. If the distance of the edge from the origin is much larger than the area of broadening, the distribution function still displays the characteristic step-like behavior. Clearly, this picture is valid for the dimensionless parameter T / T F T/T_F T/TF being small.
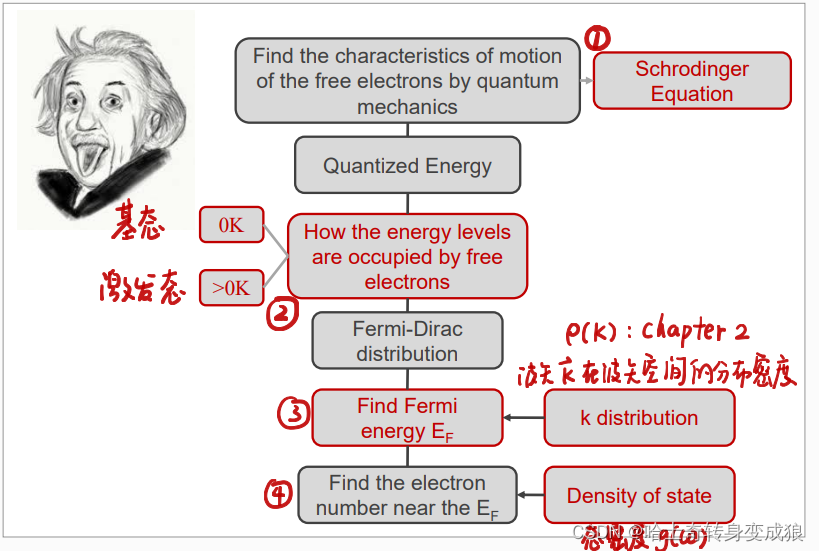
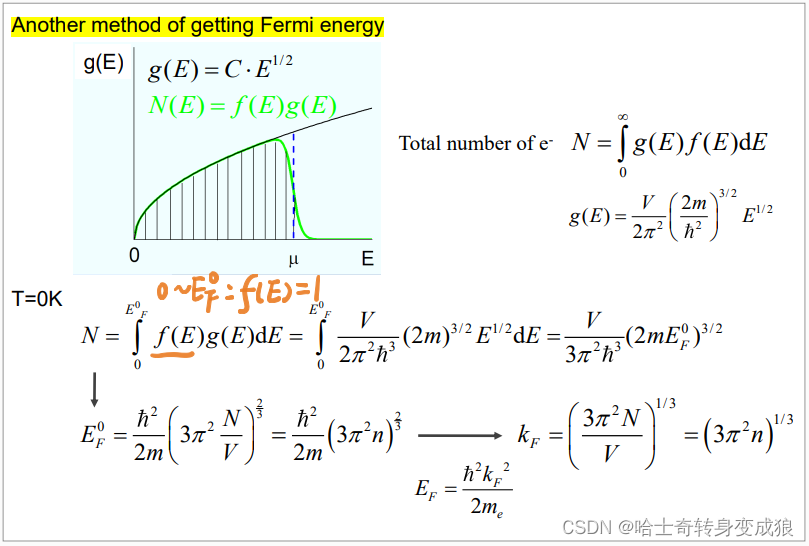
(3)计算0K时的费米能 Fermi Energy at T=0K
视频讲解:费米能和态密度
KaTeX parse error: Undefined control sequence: \k at position 20: …= \frac{(\hbar \̲k̲_F)^2}{2m}

n u m b e r o f k : V F ⋅ ρ ( k ) = ( 4 π k F 3 3 ) ( V 8 π 3 ) = k F 3 6 π 2 V number \ of \ k: \ V_F \cdot \rho(k) = \left(\frac{4\pi k_F^3}{3} \right) \left( \frac{V}{8\pi^3} \right) = \frac{k_F^3}{6\pi^2}V number of k: VF⋅ρ(k)=(34πkF3)(8π3V)=6π2kF3V
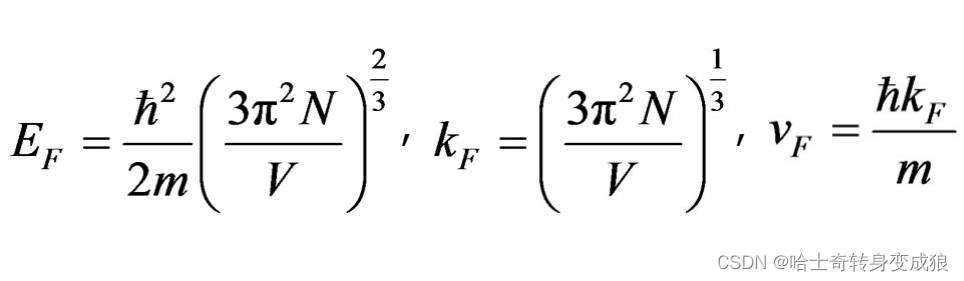
where N is the total number of electrons, n=N/V is the total number of electrons per unit volume in the alloy, m is the effective mass, ħ is the reduced Plank’s constant
Fermi temperature T F T_F TF: T F = E F k B T_F = \frac{E_F}{k_B} TF=kBEF
费米能级对应的费米球的半径是费米半径,对应的费米面是电子占据能级和不占据的分界面。
Fermi sphere: 费米面
Fermi wave vector k F k_F kF: 费米波矢 the radius of the Fermi sphere
At T=0K, inside Fermi sphere, all orbits are occupied; outside Fermi sphere, all orbits are empty.
(4)态密度 density of state
态密度:单位能量间隔电子能态(量子态或者轨道)的数量。
DOS: the number of electronic energy states (orbits) per unit energy.
g ( E ) = d Z d E g(E) = \frac{dZ}{dE} g(E)=dEdZ
In crystal dynamics, the density of states g(ω) is defined as the number of oscillators (or k) per unit frequency interval.
Each k state represents two possible electron states: (考虑自旋,一个k态对应两个可能的电子能量态)
one for spin up, the other for spin down, thus the total number of electronic states in a sphere of diameter k is: Z ( E ) = 2 ⋅ ρ ( k ) ⋅ 4 3 π k 3 = V k 3 3 π 2 Z(E) = 2\cdot \rho(\mathbf{k}) \cdot \frac{4}{3} \pi k^3 = \frac{Vk^3}{3\pi^2} Z(E)=2⋅ρ(k)⋅34πk3=3π2Vk3
consider: E = ℏ 2 k 2 2 m E = \frac{\hbar ^2 k^2}{2m} E=2mℏ2k2
g ( E ) = d Z d E = d Z d k ⋅ d k d E g(E) = \frac{dZ}{dE} = \frac{dZ}{dk}\cdot \frac{dk}{dE} g(E)=dEdZ=dkdZ⋅dEdk
∴ g ( E ) = V 2 π 2 ( 2 m ℏ 2 ) 3 / 2 \therefore g(E) = \frac{V}{2\pi^2} \left( \frac{2m}{\hbar^2}\right)^{3/2} ∴g(E)=2π2V(ℏ22m)3/2
g ( E ) = C ⋅ E 1 / 2 g(E) = C\cdot E^{1/2} g(E)=C⋅E1/2
{ 1 D : g ( E ) = C ⋅ E − 1 / 2 2 D : g ( E ) = m S π ℏ 2 3 D : g ( E ) = C ⋅ E − 1 / 2 \begin{cases} 1D: g(E) = C\cdot E^{-1/2} \\ 2D: g(E) = \frac{mS}{\pi \hbar^2} \\ 3D: g(E) = C\cdot E^{-1/2} \end{cases} ⎩ ⎨ ⎧1D:g(E)=C⋅E−1/22D:g(E)=πℏ2mS3D:g(E)=C⋅E−1/2
(5)费米能级附近的电子数量 e- number near E F E_F EF
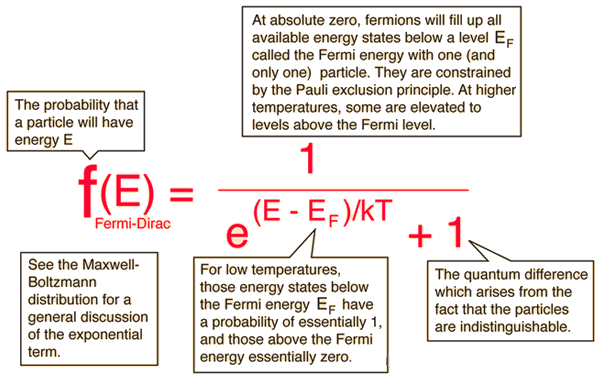
DOS g(E): the number of electronic energy states (orbits) per unit energy.
f(E): probability that an electronic energy state be occupied.
N(E):电子能量分布函数 Electron energy distribution function
N(E)dE = number of e- with energies between E and E+dE
g(E)f(E)dE = number of e- with energies between E and E+dE
N ( E ) = g ( E ) f ( E ) N(E) = g(E)f(E) N(E)=g(E)f(E)
total number of e-: N = ∈ 0 ∞ g ( E ) f ( E ) d E N = \in_0^{\infty} g(E)f(E)dE N=∈0∞g(E)f(E)dE
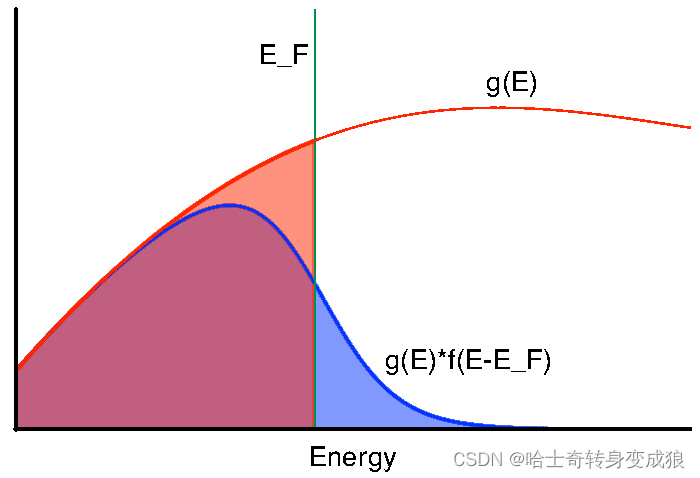
下面这个方法很合适:
(6)电子气能量 e- gas energy
Total energy for electron gas:
T=0K :
E t = ∫ E d N = ∫ E ⋅ g ( E ) f ( E ) d E = ∫ 0 E F 0 C ⋅ E 1 / 2 d E = ∫ 0 E F 0 C E 3 / 2 d E = 2 C 5 ( E F 0 ) 5 / 2 E_t = \int EdN = \int E\cdot g(E)f(E)dE = \int_0^{E_F^0} C\cdot E^{1/2} dE = \int_0^{E_F^0} CE^{3/2}dE = \frac{2C}{5}(E_F^0)^{5/2} Et=∫EdN=∫E⋅g(E)f(E)dE=∫0EF0C⋅E1/2dE=∫0EF0CE3/2dE=52C(EF0)5/2
Average energy for free electrons:
E ˉ = E t N = 3 5 E F 0 \bar E = \frac{E_t}{N} = \frac{3}{5}E_F^0 Eˉ=NEt=53EF0
E t = 3 5 N E F 0 E_t = \frac{3}{5}NE_F^0 Et=53NEF0
At T=0K,the average energy of a free electron is 60% of the Femi energy.
T>0K :
E t = ∫ E ⋅ g ( E ) f ( E ) d E = C ∫ 0 ∞ E 3 / 2 1 e ( E − E F ) / k B T + 1 = … = 3 5 N E F 0 [ 1 + 5 12 π 2 ( k B T E F 0 ) 2 ] \begin{align} E_t &=\int E\cdot g(E)f(E)dE \\ &= C \int_0^{\infty} E^{3/2} \frac{1}{e^{(E-E_F)/k_B T}+1} \\ & =\dots \\ &= \frac{3}{5}N E_F^0 [1+ \frac{5}{12}\pi^2 (\frac{k_B T}{E_F^0})^2] \end{align} Et=∫E⋅g(E)f(E)dE=C∫0∞E3/2e(E−EF)/kBT+11=…=53NEF0[1+125π2(EF0kBT)2]
第一项是零点能,第二项由于分母的费米能很大所以可以忽略不计。
温度升高,热容涨幅不明显
E F = E F 0 [ 1 − 1 12 π 2 ( k B T E F 0 ) 2 ] = E F 0 [ 1 − π 2 12 ( T T F ) 2 ] ≈ E F 0 E_F = E_F^0 \left[1- \frac{1}{12}\pi^2 (\frac{k_B T}{E_F^0})^2 \right] = E_F^0 \left[1-\frac{\pi^2}{12}\left( \frac{T}{T_F}\right)^2 \right] \approx E_F^0 EF=EF0[1−121π2(EF0kBT)2]=EF0[1−12π2(TFT)2]≈EF0
相关文章:
chapter 3 Free electrons in solid - 3.1 自由电子模型
3.1 自由电子模型 Free electron model 研究晶体中的电子: 自由电子理论:不考虑离子实能带理论:考虑离子实(周期性势场)的作用 3.1.1 德鲁德模型 Drude Model - Classical Free Electron Model (1)德鲁德模型 德鲁…...

搭建博客时前端美化内容CSS推荐
一、背景 在搭建博客的时候,发现对其markdown文章内容进行渲染的时候,样式调整比较花费时间 二、解决思路 自己适配样式 缺点:ROI不高 使用开源的markdown的样式:github-markdown-css 三、实现教程 1、NPM安装 npm install …...

Linux中 socket编程中多进程/多线程TCP并发服务器模型
一、循环服务器(while)【不常用】 一次只能处理一个客户端的请求,等这个客户端退出后,才能处理下一个客户端。缺点:循环服务器所处理的客户端不能有耗时操作。 模型 sfd socket(); bind(); listen(); while(1) {newfd accept();while(1){r…...
【内网穿透】如何实现在外web浏览器远程访问jupyter notebook服务器
文章目录 前言1. Python环境安装2. Jupyter 安装3. 启动Jupyter Notebook4. 远程访问4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5. 固定公网地址 前言 Jupyter Notebook,它是一个交互式的数据科学和计算环境,支持多种编程语言,如…...
win10下如何安装ffmpeg
安装ffmpeg之前先安装win10 绿色软件管理软件:scoop. Scoop的基本介绍 Scoop是一款适用于Windows平台的命令行软件(包)管理工具,这里是Github介绍页。简单来说,就是可以通过命令行工具(PowerShell、CMD等…...
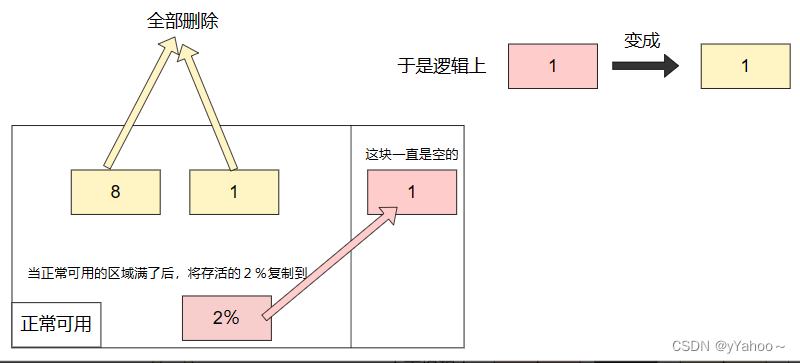
分代收集 + 垃圾回收算法
分代假说 1. 弱分代假说(Weak Generational Hypothesis):绝大多数对象都是朝生夕灭的 2. 强分代假说(Strong Generational Hypothesis):熬过越多次垃圾收集过程的对象就越难以消亡 3. 跨代引用假说&…...

第三届“赣政杯”网络安全大赛 | 赛宁筑牢安全应急防线
为持续强化江西省党政机关网络安全风险防范意识,提高信息化岗位从业人员基础技能,提升应对网络安全风险处置能力。由江西省委网信办、江西省发展改革委主办,江西省大数据中心、国家计算机网络与信息安全管理中心江西分中心承办࿰…...

CHATGPT源码简介与使用指南
CHATGPT源码的基本介绍 CHATGPT源码备受关注,它是一款基于人工智能的聊天机器人,旨在帮助开发者快速搭建自己的聊天机器人,无需编写代码。下面是对CHATGPT搭建源码的详细介绍。 CHATGPT源码的构建和功能 CHATGPT源码是基于Google的自然语言…...

【C++精华铺】8.C++模板初阶
目录 1. 泛型编程 2. 函数模板 2.1 函数模板的概念及格式 2.2 函数模板的原理 2.3 模板的实例化 2.4 模板参数的匹配原则 3. 类模板 3.1 类模板格式 3.2 类模板的实例化 1. 泛型编程 什么是泛型编程?泛型编程是避免使用某种具体类型而去使用某种通用类型来进行…...

离谱的Bug
离谱的 Bug Bug 情况发现 Bug修改 Bug其他感受历史 Bug火星Spirit号Mars Global Surveyor任务 Bug 情况 有一次,我在开发一个网页应用程序时,遇到了一个令人目瞪口呆的Bug。这个Bug出现在一个特定的页面上,当用户点击某个按钮时,…...
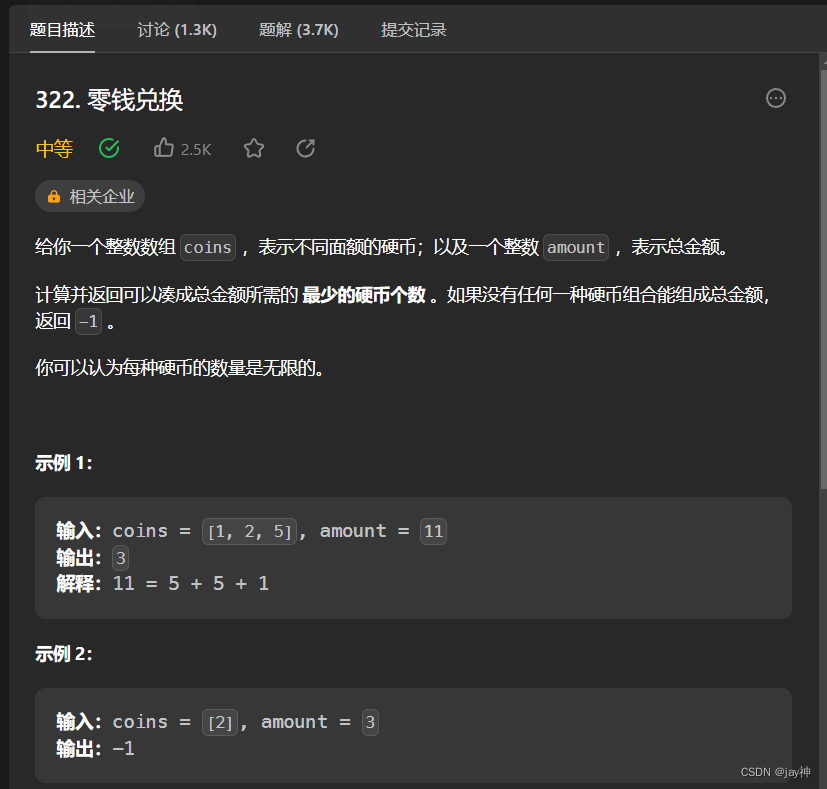
leetcode 322. 零钱兑换
本题属于完全背包问题,但要求最少的硬币个数。于是设定dp数组的含义dp[i]:总金额为i时,能凑成i的最少硬币个数。 需要注意初始化dp数组时,除0以外的其他地方需要初始化为INT_MAX以保证在递推过程中能被正确的覆盖。 代码如下: …...
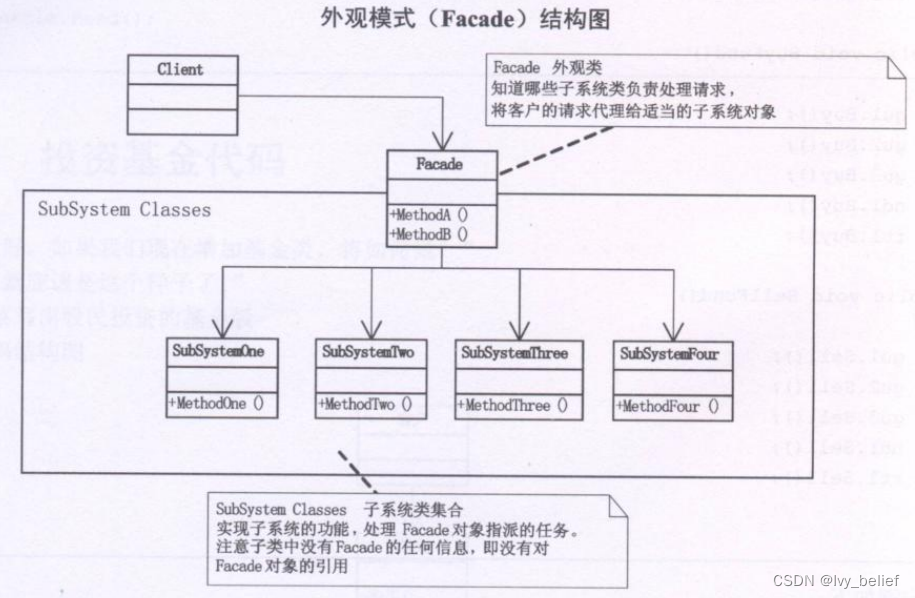
(二)结构型模式:6、外观模式(Facade Pattern)(C++实例)
目录 1、外观模式(Facade Pattern)含义 2、外观模式的UML图学习 3、外观模式的应用场景 4、外观模式的优缺点 5、C实现外观模式的简单实例 1、外观模式(Facade Pattern)含义 外观模式(Facade Pattern)…...
docker的资源控制管理——Cgroups
目录 一、对CPU使用率的控制 1.1 CPU 资源控制 1.2 cgroups有四大功能 1.3 设置cpu使用率上限 查看周期限制和cpu配额限制 进行cpu压力测试然后修改每个周期的使用cpu的时间,查看cpu使用率 1.4 设置cpu资源占用比(设置多个容器时才有效…...
less学习语法
1.CSS函数的补充 1.rgb/rgba/translate/rotate/scale 2.非常好用的css函数: var:使用css定义的变量calc:计算css值,通常用于计算元素的大小或位置blur:毛玻璃(高斯模糊)效果gradient:颜色渐变函数 var:定义变量 css中可以自定…...
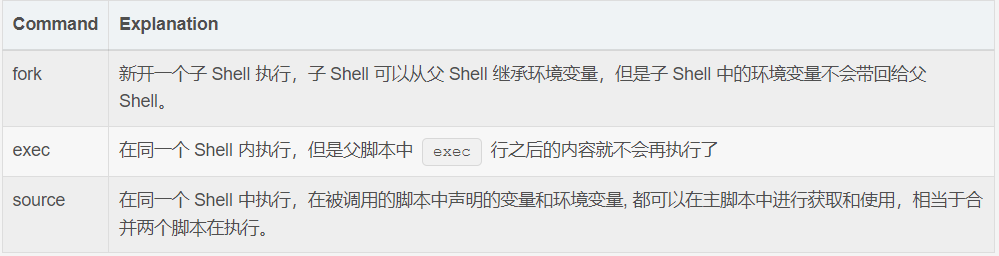
在 SHELL 脚本中调用另一个 SHELL 脚本(报错: go: not found)
文章目录 在 SHELL 脚本中调用另一个 SHELL 脚本(报错: go: not found)在 SHELL 脚本中调用另一个 SHELL 脚本一个脚本sudo调另外一个脚本,报错(报错: go: not found) 在 SHELL 脚本中调用另一个…...
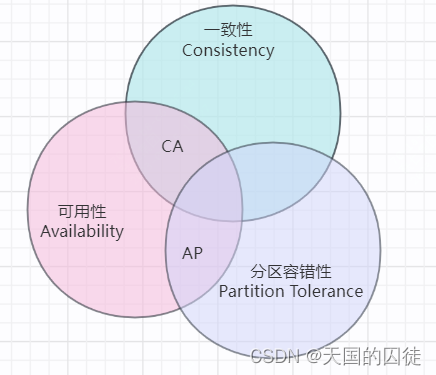
07微服务的事务管理机制
一句话导读 在单体应用程序中,事务通常是在单个数据库或单个操作系统中管理的,而在微服务架构中,事务需要跨越多个服务和数据库,这就使得事务管理变得更加复杂和困难。 目录 一句话导读 一、微服务事务管理的定义和意义 二、微…...
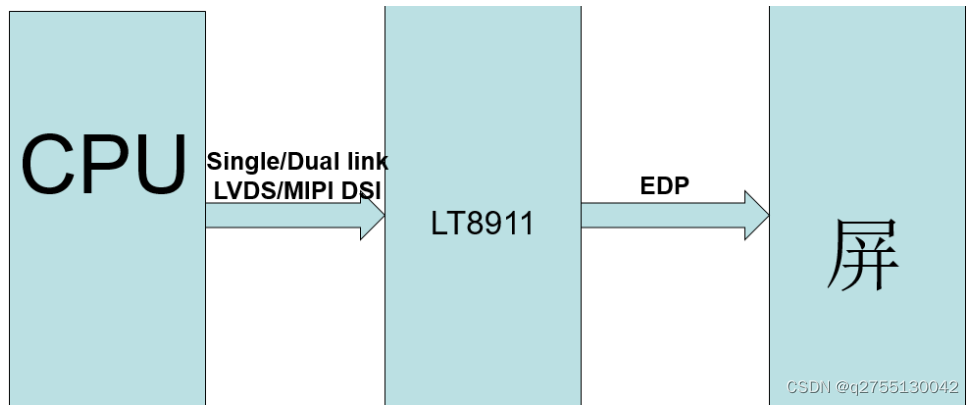
CS5523规格书|MIPI转EDP方案设计|替代LT8911芯片电路原理|ASL集睿致远CS替代龙讯
ASL芯片(集睿致远) CS5523是一款MIPI DSI输入,DP/e DP输出转换芯片,可pin to pin替代LT8911龙讯芯片。 MIPI DSI 最多支持 4 个通道,每个通道的最大运行速度为 1.5Gps。对于DP 1.2输出,它支持1.62Gbps和2.…...

【制作npm包5】npm包制作完整教程,我的第一个npm包
制作npm包目录 本文是系列文章, 作者一个橙子pro,本系列文章大纲如下。转载或者商业修改必须注明文章出处 一、申请npm账号、个人包和组织包区别 二、了解 package.json 相关配置 三、 了解 tsconfig.json 相关配置 四、 api-extractor 学习 五、npm包…...

QT:定时器事件
定时器第一种办法: 1.利用事件timerEvent,在帮助文档中找到该字段:[override virtual protected] void QTimer::timerEvent(QTimerEvent *e) 重写该虚函数 //重写定时器事件void timerEvent(QTimerEvent *e);2.启动定时器startTimer(1000); …...
GitHub Actions自动化部署+定时百度链接推送
前言 最近用VuePress搭建了一个静态网站,由于是纯静态的东西,每次修改完文章都要重新打包上传很是麻烦。虽然vuepress-theme-vdoing主题作者提供了GitHub Actions自动化部署的教程文章,但是过于简陋且是19年发布的。。 1. 创建一个GitHub仓…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...