P1006 [NOIP2008 提高组] 传纸条
P1006 [NOIP2008 提高组] 传纸条
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 四维dp
- 三维dp
- AC四维代码:
- AC三维代码:
题目描述
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。一次素质拓展活动中,班上同学安排坐成一个 m m m 行 n n n 列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。幸运的是,他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标 ( 1 , 1 ) (1,1) (1,1),小轩坐在矩阵的右下角,坐标 ( m , n ) (m,n) (m,n)。从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙。反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用 0 0 0 表示),可以用一个 [ 0 , 100 ] [0,100] [0,100] 内的自然数来表示,数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有两个用空格隔开的整数 m m m 和 n n n,表示班里有 m m m 行 n n n 列。
接下来的 m m m 行是一个 m × n m \times n m×n 的矩阵,矩阵中第 i i i 行 j j j 列的整数表示坐在第 i i i 行 j j j 列的学生的好心程度。每行的 n n n 个整数之间用空格隔开。
输出格式
输出文件共一行一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
样例 #1
样例输入 #1
3 3
0 3 9
2 8 5
5 7 0
样例输出 #1
34
提示
【数据范围】
对于 30 % 30\% 30% 的数据,满足 1 ≤ m , n ≤ 10 1 \le m,n \le 10 1≤m,n≤10。
对于 100 % 100\% 100% 的数据,满足 1 ≤ m , n ≤ 50 1 \le m,n \le 50 1≤m,n≤50。
【题目来源】
NOIP 2008 提高组第三题。
思路
四维dp
这题就是说要找到两条互不重合的两条最大线路。虽然说一个是从左上角出发,一个是从右下角出发,不过其实两个都从左上角出发就行了,这样比较好思考,也比较好写
一眼看过去,dp!!!最好想到的就是四维dp:
d p [ i ] [ j ] [ u ] [ v ] dp[i][j][u][v] dp[i][j][u][v]表示第一条线路到达了 ( i , j ) (i,j) (i,j),第二条线路到达了 ( u , v ) (u,v) (u,v)
当然,两条线路不能走到同一个点,所以在循环 i , j , u , v i,j,u,v i,j,u,v时, v v v要从 j + 1 j+1 j+1开始,
或者判断当两个点重合时, d p [ i ] [ j ] [ u ] [ v ] dp[i][j][u][v] dp[i][j][u][v]减去一个人的好心程度
四维的状态转移方程比较好想:
f[i][j][k][l]=max( f[i][j-1][k-1][l] , max(f[i-1][j][k][l-1] , max(f[i][j-1][k][l-1] , f[i-1][j][k-1][l]) ) )+a[i][j]+a[k][l]
a是输入的好心程度!!!
怎么样?很简单吧?
不过当数据再大一点的时候就不能用四维的了,这个 1 ≤ m , n ≤ 50 1≤m,n≤50 1≤m,n≤50着实有点水,所以我们要用三维的,当然三维的也很好理解哦。
三维dp
我们可以发现:两条线路走的总步数是一样的(即 i + j i+j i+j等于 u + v u+v u+v),所以我们可以只枚举两条线路的纵坐标或者横坐标就可以了。(我枚举的是横坐标)
那么我们现在的 d p [ k ] [ i ] [ j ] dp[k][i][j] dp[k][i][j]就表示一共走了k步,第一条线路在第i列上,第二条线路在第j列上时的最大好心程度
注意!!!dp数组的第一维要开到 n + m n+m n+m以上,因为这个棋矩阵最多可以走到大概 n + m n+m n+m步
那么我们的状态转移方程为:
dp[k][i][j]=max_(dp[k-1][i-1][j-1],dp[k-1][i][j],dp[k-1][i-1][j],dp[k-1][i][j-1])+a[i][k-i]+a[j][k-j];
max_ 是一个函数,就是求着四个数的最大值不过你也可以写三个max
其中:
d p [ k − 1 ] [ i − 1 ] [ j − 1 ] dp[k-1][i-1][j-1] dp[k−1][i−1][j−1]表示:在上一步时两条线路都向下移动;
d p [ k − 1 ] [ i ] [ j ] dp[k-1][i][j] dp[k−1][i][j]表示:在上一步时两条线路都向右移动;
d p [ k − 1 ] [ i − 1 ] [ j ] dp[k-1][i-1][j] dp[k−1][i−1][j]表示:在上一步时一条向下,一条向右;
d p [ k − 1 ] [ i ] [ j − 1 ] dp[k-1][i][j-1] dp[k−1][i][j−1]表示:在上一步时一条向右,一条向下;
a a a数组为输入的好心程度
差不多就这样,是不是很简单?看看代码吧:
含有注释,放心食用:
AC四维代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 55
using namespace std;
int a[N][N],f[N][N][N][N];
void work(int i,int j,int k,int l)
{int Max=0;Max=max(Max,f[i-1][j][k-1][l]);//这里可以合并,看个人喜好 Max=max(Max,f[i-1][j][k][l-1]);Max=max(Max,f[i][j-1][k-1][l]);Max=max(Max,f[i][j-1][k][l-1]);f[i][j][k][l]=Max+a[i][j];if(i!=k||j!=l)//去重,因为题目不允许走到同一个点 f[i][j][k][l]+=a[k][l];
}
int main()
{int m,n,i,j,k,l;scanf("%d%d",&m,&n);for(i=1;i<=m;++i)for(j=1;j<=n;++j)scanf("%d",&a[i][j]);for(i=1;i<=m;++i)for(j=1;j<=n;++j)for(u=1;u<=m;++u)for(v=1;v<=n;++v)work(i,j,u,v);printf("%d",f[m][n][m][n]);return 0;
}AC三维代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,a[101][101],dp[201][101][101];
int max_(int a,int b,int c,int d){return max(a,max(b,max(c,d)));//求最大的
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}for(int k=2;k<=n+m;k++){//枚举步数 for(int i=1;i<=n;i++){//枚举横坐标 for(int j=1;j<=n;j++){//枚举横坐标 int l1=k-i,l2=k-j;if(l1<1||l1>m||l2<1||l2>m) continue;int t=a[i][l1];if(i!=j) t+=a[j][l2];//如果没有重复就加上 dp[k][i][j]=max_(dp[k-1][i-1][j-1],dp[k-1][i][j],dp[k-1][i-1][j],dp[k-1][i][j-1]);//求最大的 (函数) dp[k][i][j]+=t;//加上当前位置的好心程度 }}}cout<<dp[n+m][n][n];//输出 return 0;
}相关文章:

P1006 [NOIP2008 提高组] 传纸条
P1006 [NOIP2008 提高组] 传纸条 题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 思路四维dp三维dp AC四维代码:AC三维代码: 题目描述 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。一次素质拓展活动中&#…...
杭电比赛总结
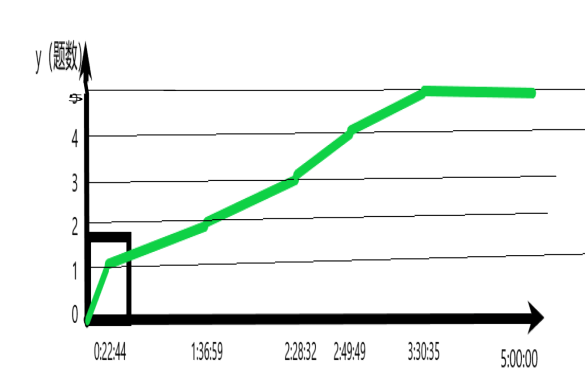
我们的队伍:team013 另外两队:team014、team015 今天是我第一次打杭电,发现杭电多数都是猜结论题 先给一下我们的提交数据 Submit TimeProblem IDTimeMemoryJudge Status4:59:59101115 MS1692 KWrong Answer4:59:55101115 MS1684 KWrong…...
dom靶场
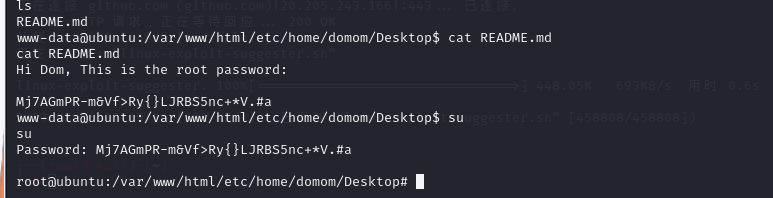
靶场下载地址: https://www.vulnhub.com/entry/domdom-1,328/ 一、信息收集 获取主机ip nmap -sP 192.168.16.0/24netdiscover -r 192.168.16.0/24端口版本获取 nmap -sV -sC -A -p 1-65535 192.168.16.209开放端口只有80 目录扫描 这里扫描php后缀的文件 g…...

go struct 的常见问题
go struct 的常见问题 1. 什么是struct?2. 如何声明、定义和创建一个struct?3. struct和其他数据类型(如数组、切片、map等)有什么区别?4. 如何访问struct字段?5. struct是否支持继承,是否支持重…...

Linux系统下的性能分析命令
在 Linux 系统下,有许多用于性能分析和调试的命令和工具,可以帮助您识别系统瓶颈、优化性能以及调查问题。本文将介绍在性能分析过程中,可能使用到的一些命令。 以下是一些常用的性能分析命令和工具汇总: 命令功能简述top用于实…...
第十三课:QtCmd 命令行终端应用程序开发
功能描述:开发一个类似于 Windows 命令行提示符或 Linux 命令行终端的应用程序 一、最终演示效果 QtCmd 不是因为它是 Qt 的组件,而是采用 Qt 开发了一个类似 Windows 命令提示符或者 Linux 命令行终端的应用程序,故取名为 QtCmd。 上述演示…...
Jmeter进阶使用:BeanShell实现接口前置和后置操作
一、背景 我们使用Jmeter做压力测试或者接口测试时,除了最简单的直接对接口发起请求,很多时候需要对接口进行一些前置操作:比如提前生成测试数据,以及一些后置操作:比如提取接口响应内容中的某个字段的值。举个最常用…...

【知识分享】高防服务器的防御机制
【知识分享】高防服务器的防御机制 易受到攻击的网站选择接入高防服务更安全,大家对于这个都清楚!但是对于高防服务如何实现防御来保障安全的,又了解多少呢?今天壹基比小源(贰伍壹叁壹叁壹贰玖捌)就来说说高防服务实现防御的常规…...
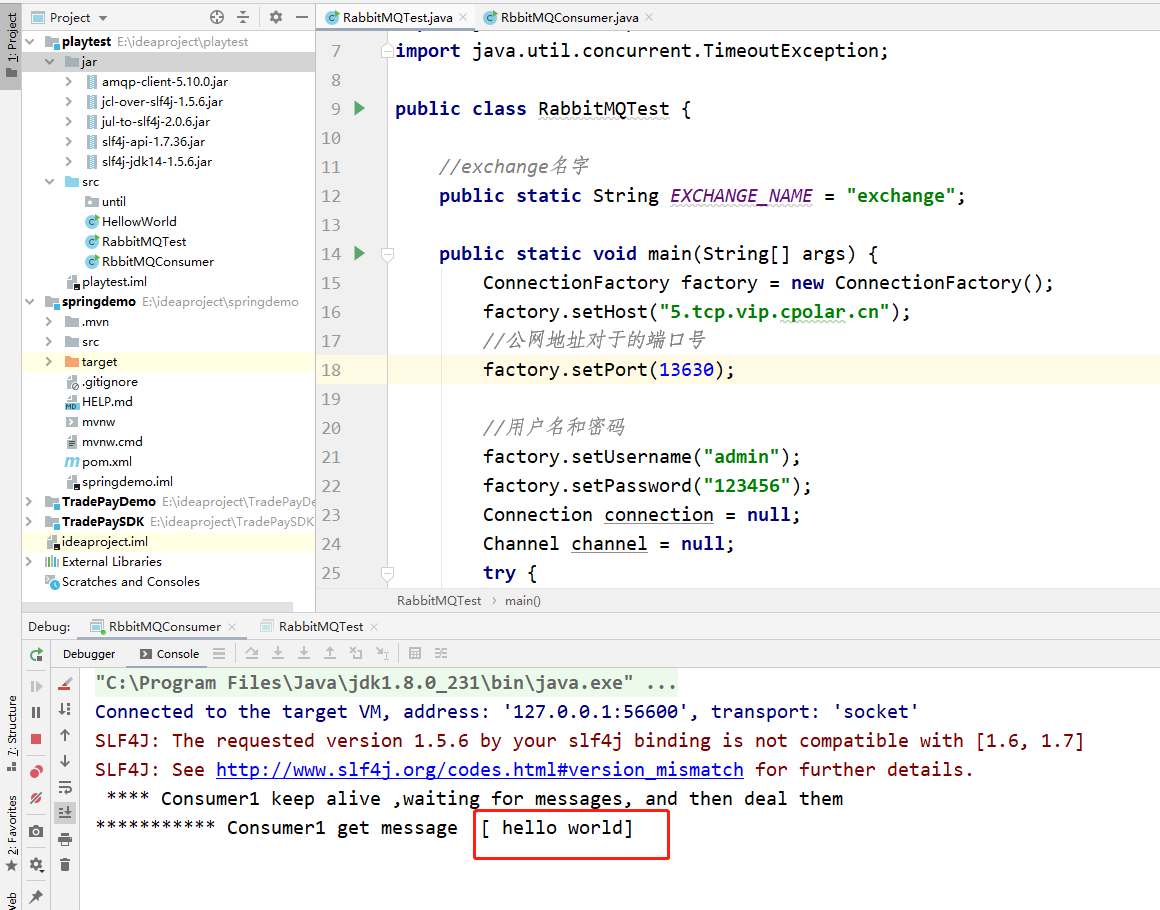
内网穿透-外远程连接中的RabbitMQ服务
文章目录 前言1.安装erlang 语言2.安装rabbitMQ3. 内网穿透3.1 安装cpolar内网穿透(支持一键自动安装脚本)3.2 创建HTTP隧道 4. 公网远程连接5.固定公网TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址 前言 RabbitMQ是一个在 AMQP(高级消息队列协议)基…...
驱动DAY4 字符设备驱动分步注册和ioctl函数点亮LED灯
头文件 #ifndef __HEAD_H__ #define __HEAD_H__ typedef struct{unsigned int MODER;unsigned int OTYPER;unsigned int OSPEEDR;unsigned int PUPDR;unsigned int IDR;unsigned int ODR; }gpio_t; #define PHY_LED1_ADDR 0X50006000 #define PHY_LED2_ADDR 0X50007000 #d…...

Python爬虫——scrapy_当当网图书管道封装
创建爬虫项目 srcapy startproject scrapy_dangdang进入到spider文件里创建爬虫文件(这里爬取的是青春文学,仙侠玄幻分类) srcapy genspider dang http://category.dangdang.com/cp01.01.07.00.00.00.html获取图片、名字和价格 # 所有的se…...
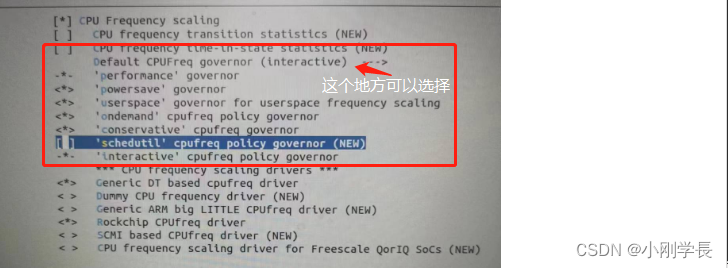
Linux下如何修改CPU 电源工作模式
最近处理一起历史遗留问题,感觉很爽。 现象: 背景:设备采用ARM,即rk3568处理器,采用Linux系统;主要用于视觉后端处理 现象:当软件运行一段时间,大概1个小时(也不是很固定…...
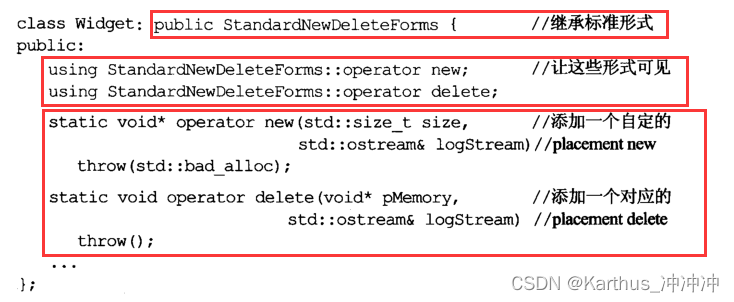
Effective C++学习笔记(8)
目录 条款49:了解new-handler的行为条款50:了解new和delete的合理替换时机条款51:编写new和delete时需固守常规条款52:写了placement new也要写placement delete条款53:不要轻忽编译器的警告条款54:让自己熟…...
学校如何公布录取情况表?这个不用技术的方法,小白老师都能轻松制作
作为一名教师,我深切了解学生和家长们对录取情况的关注和重视。为了满足他们的需求,我们学校一直致力于改进公布录取情况的方式和效果。在本篇文章中,我将向您介绍我们学校独特的录取查询系统,并分享我们选择这种方式的原因。 我…...

Chart GPT免费可用地址共享资源
GPT4.0: https://gpt4e.ninvfeng.xyz github:https://github.com/ninvfeng/chatgpt4 WeUseAi:https://chatb.weuseai.pro AI.LS:https://n7.gpt03.xyz ChatX (iOS/macOS应用):https://itunes.apple.com/app/id6446304087 ch…...
)
设计模式十八:中介者模式(Mediator Pattern)
在中介者模式中,多个对象之间不再直接相互通信,而是通过一个中介者对象进行通信。这可以减少对象之间的依赖关系,使系统更加模块化。中介者模式适用于当对象之间的通信逻辑变得复杂,导致代码难以维护和理解时。 中介者模式使用场…...

神经网络基础-神经网络补充概念-12-向量化逻辑回归的梯度输出
代码实现 import numpy as npdef sigmoid(z):return 1 / (1 np.exp(-z))def compute_loss(X, y, theta):m len(y)h sigmoid(X.dot(theta))loss (-1/m) * np.sum(y * np.log(h) (1 - y) * np.log(1 - h))return lossdef compute_gradient(X, y, theta):m len(y)h sigmoi…...

2023-08-16力扣每日一题
链接: 2682. 找出转圈游戏输家 题意: 环形1到n,从1开始,每次移动 第i次*k ,当移动到出现过的序号时停下, 求没移动到的数字 解: 简单模拟题,我也以为有数学做法,可…...

耗资170亿美元?三星电子在得克萨斯州建设新的半导体工厂
据报道,三星电子在得克萨斯州泰勒市建设的新的半导体工厂预计将于2024年下半年投入运营。这座工厂将成为三星电子在美国的第二座芯片代工厂,与位于得克萨斯州奥斯汀市的第一座工厂相距不远。 此次投资将耗资约170亿美元,显示了三星电子在半导…...
)
黑马项目一阶段面试58题 Web14题(一)
一、什么是AJAX 异步的JavaScript和XML。用来做前端和后端的异步请求的技术。 异步请求:只更新部分前端界面的请求,做到局部更新。 比如注册,提示用户名已存在而整个页面没有动 比如百度图片搜索美女,进度条越变越短ÿ…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
