看见统计——第三章 概率分布
看见统计——第三章 概率分布
参考
- https://github.com/seeingtheory/Seeing-Theory
- 中心极限定理
概率分布描述了随机变量取值的规律。
随机变量Random Variables
🔥 定义:将样本空间中的结果映射到实数的函数 XXX 称为随机变量(random variable),记为X:Ω→X:\Omega\toX:Ω→
例如,在抛硬币问题中,样本空间就是 Ω=正面,背面\Omega={正面,背面}Ω=正面,背面,随机变量有X(正面)=1,X(背面)=0X(正面)=1,X(背面)=0X(正面)=1,X(背面)=0。
随机变量是一个函数,它用数字来表示一个可能出现的事件。你可以定义你自己的随机变量,然后生成一些样本来观察它的经验分布。
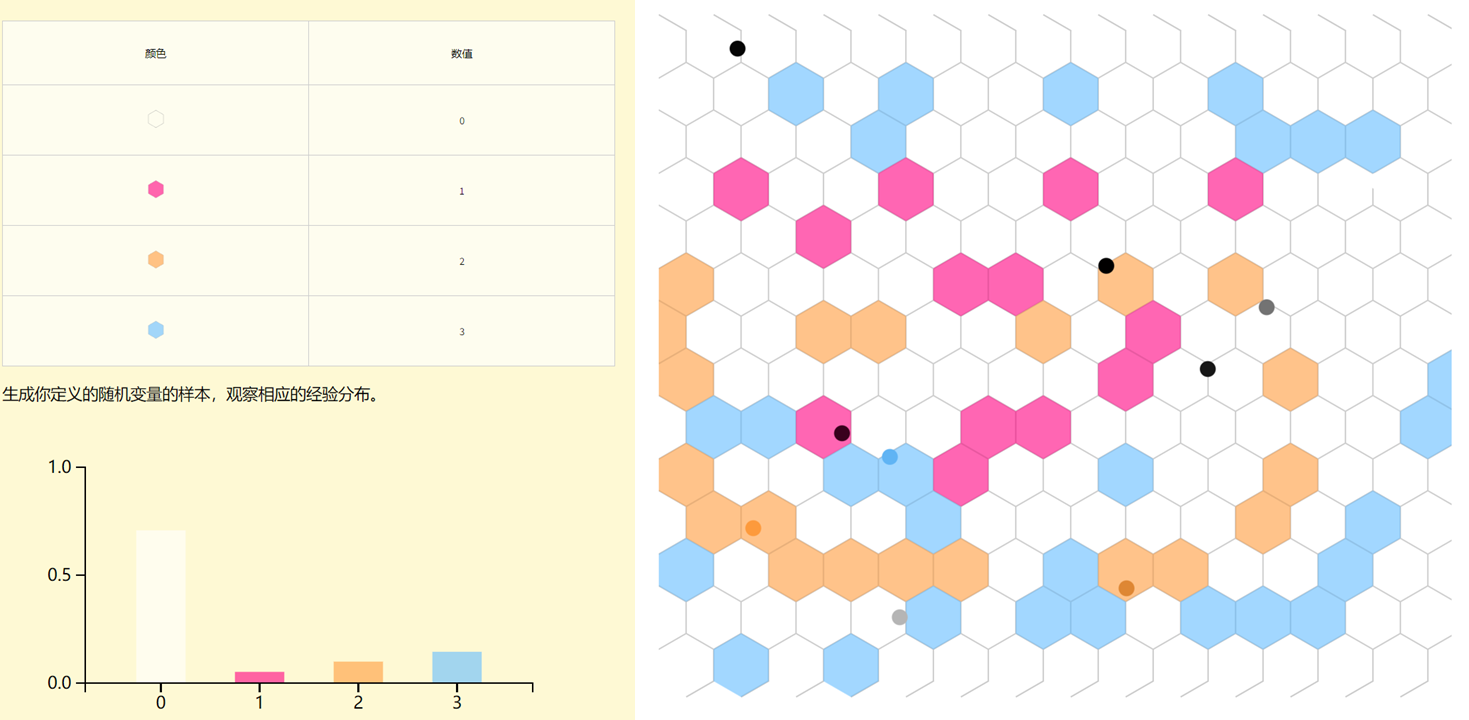
随机变量的独立性
🔥 定义:假设XXX和YYY是定义在某个样本空间ΩΩΩ上的两个随机变量。对于任意的两个子集AAA 和 BBB ,当满足:
P(X∈A,Y∈B)=P(X∈A)P(Y∈B)P(X\in A,Y\in B)=P(X\in A)P(Y\in B) P(X∈A,Y∈B)=P(X∈A)P(Y∈B)
时,我们说 XXX 和 YYY 是独立的随机变量
再来证明:如果 XXX 和 YYY 是独立的随机变量,那么 E[XY]=E[X]E[Y]E[XY]=E[X]E[Y]E[XY]=E[X]E[Y]。定义随机变量 Z(ω)=X(ω)Y(ω)Z(\omega)=X(\omega)Y(\omega)Z(ω)=X(ω)Y(ω),根据期望的定义,左式可以写成:
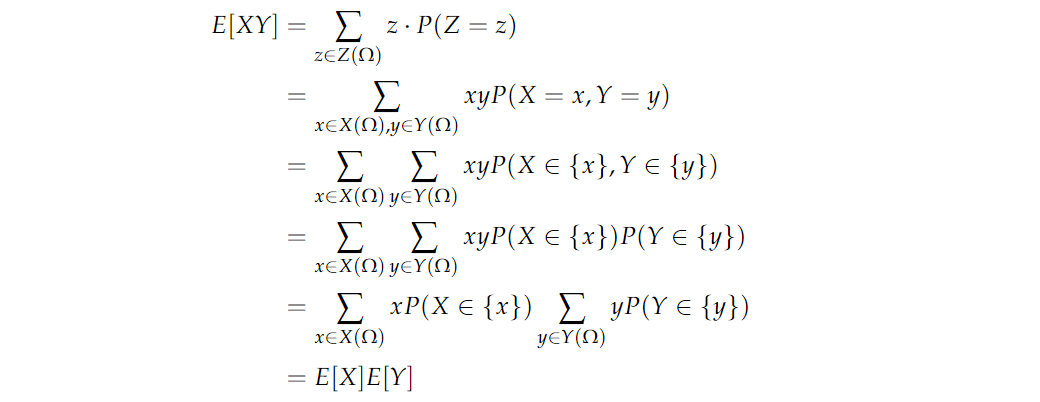
离散型和连续型随机变量Discrete and Continuous
常见的随机变量类型有两种:离散型随机变量和连续型随机变量。
离散型随机变量
一个离散型随机变量可能的取值范围只有有限个或可列个值。离散型随机变量的定义是:如果 XXX 是一个随机变量,存在非负函数 f(x)f(x)f(x) 和 F(x)F(x)F(x),使得:
P(X=x)=f(x)P(X<x)=F(x)P(X=x) = f(x) \\ P(X < x) = F(x) P(X=x)=f(x)P(X<x)=F(x)
则称 XXX 是一个离散型随机变量。
分布函数F(x)F(x)F(x):Cumulative Distribution Function, 简称CDF。
概率质量函数f(x)f(x)f(x):probability mass function,简写为PMF。是离散随机变量在各特定取值上的概率。
图示中黄色曲线为PMF,橙色曲线为CDF。
例如,我们的掷硬币产生了一个随机变量 XXX ,它只能接受集合{0,1}\{0,1\}{0,1}中的值。因此, XXX 是一个离散的随机变量。然而,离散随机变量仍然可以具有无穷多个值,如下所示。
泊松分布Poisson
泊松分布表示了一个事件在固定时间或者空间中发生的次数。泊松分布的参数 λλλ 是单位时间(或单位面积)内随机事件的平均发生次数。比方说,我们可以用泊松分布来刻画流星雨或者足球比赛中的进球数。
在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率 λλλ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布 $P(\lambda) $。因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位。(在早期学界认为人类行为是服从泊松分布,2005年在nature上发表的文章揭示了人类行为具有高度非均匀性。)
设随机变量 XXX 服从参数为 λλλ(k∈Nk\in\Nk∈N) 的泊松分布,即
P(X=k)=λxe−λk!P(X=k) =\dfrac{\lambda^{x}e^{-\lambda}}{k!} P(X=k)=k!λxe−λ
描述这种分布的简写是 X∼Poi(λ)X∼Poi(λ)X∼Poi(λ)。因为 kkk 可以是 N\NN 中的任何数字,所以我们的随机变量 XXX 在无穷多个数字上具有正的概率。然而,由于 NNN 是可数的,XXX 仍然被认为是离散型随机变量。
| PMF | 期望 | 方差 |
|---|---|---|
| f(x;λ)=λxe−λx!f(x;\lambda) = \dfrac{\lambda^{x}e^{-\lambda}}{x!}f(x;λ)=x!λxe−λ | λ\lambdaλ | λ\lambdaλ |
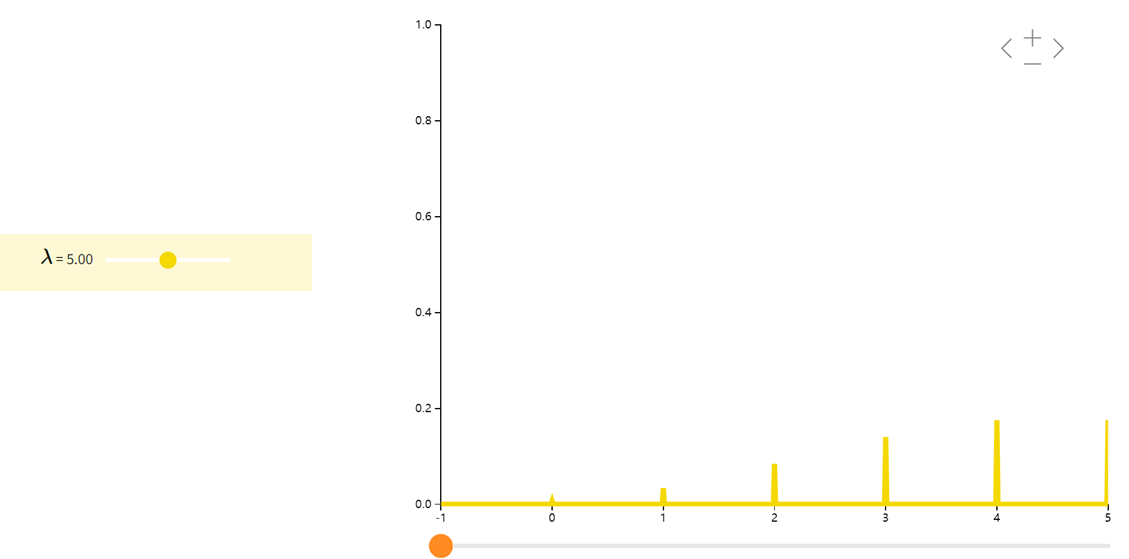
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当 n≥20,p≤0.05n\ge20,p\le0.05n≥20,p≤0.05 时,就可以用泊松公式近似得计算。
伯努利分布Bernoulli
如果一个随机变量 XXX 只取值 0 或 1,概率分布是
P(X=1)=p,P(X=0)=1−pP(X=1)=p,\quad P(X=0)=1-p P(X=1)=p,P(X=0)=1−p
则称 XXX 符合伯努利分布(Bernoulli)。我们常用伯努利分布来模拟只有两种结果的试验,如抛硬币。
| PMF | 期望 | 方差 |
|---|---|---|
| f(x;p)={pif x=11−pif x=0f(x;p) = \begin{cases} p & \text{if } x = 1 \\ 1-p & \text{if } x = 0 \end{cases}f(x;p)={p1−pif x=1if x=0 | ppp | p(1−p)p(1-p)p(1−p) |
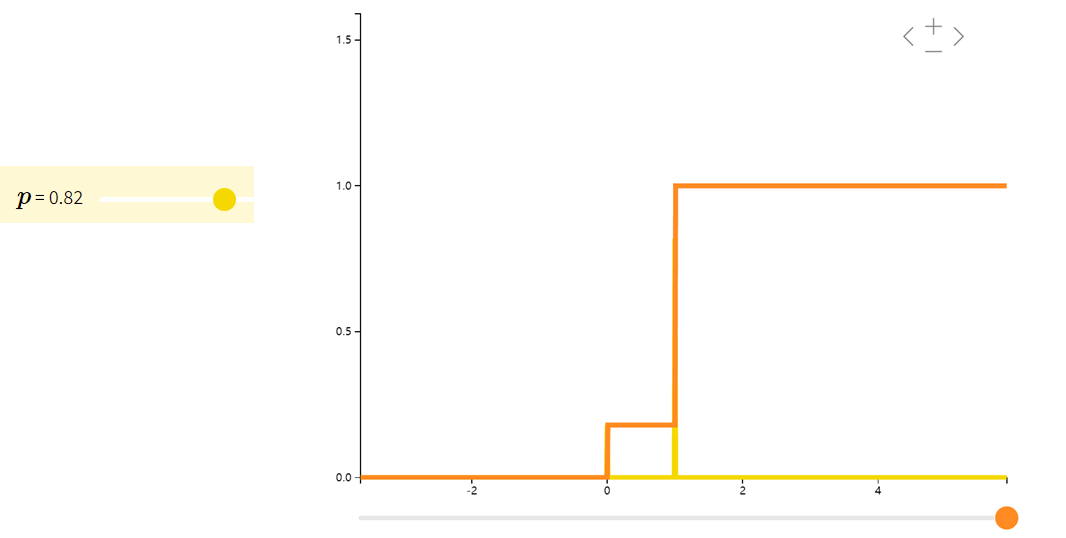
二项分布Binomial
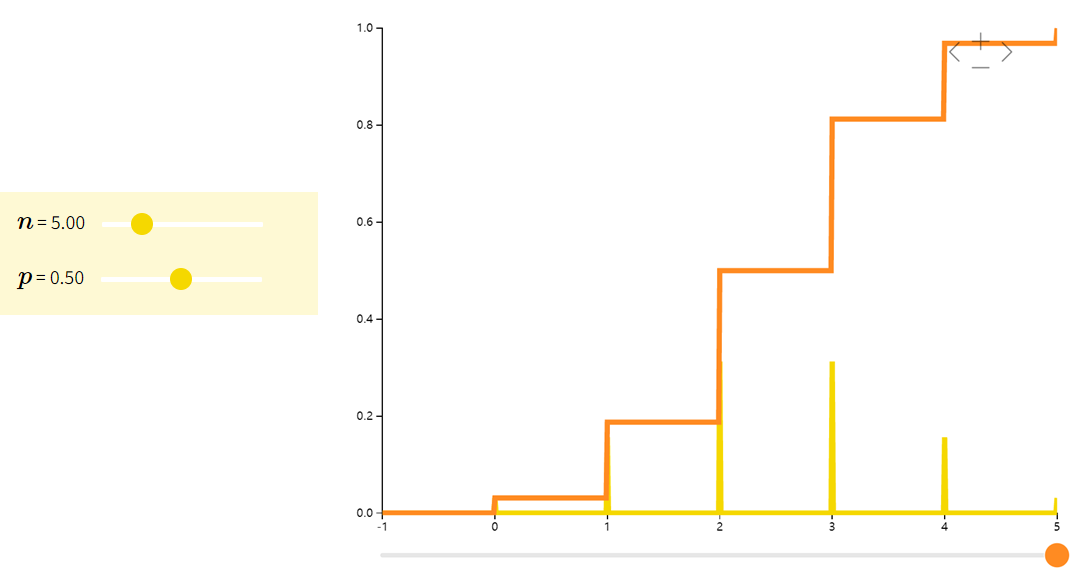
如果随机变量 XXX 是 nnn 个参数为 ppp 的独立伯努利随机变量之和,则称 XXX 是二项分布(binomial)。我们常用二项分布来模拟若干独立同分布的伯努利试验中的成功次数。比如说,抛五次硬币,其中正面的次数可以用二项分布来表示:Bin(5,1/2)Bin(5,1/2)Bin(5,1/2)。
| PMF | 期望 | 方差 |
|---|---|---|
| f(x;n,p)=(nx)px(1−p)n−xf(x; n,p) = \binom{n}{x}p^{x}(1-p)^{n-x}f(x;n,p)=(xn)px(1−p)n−x | npnpnp | np(1−p)np(1-p)np(1−p) |
例如。P(X=2)=C52(12)5=1032=0.3125P(X=2)=C_5^2(\frac{1}{2})^5=\frac{10}{32}=0.3125P(X=2)=C52(21)5=3210=0.3125
几何分布Geometric
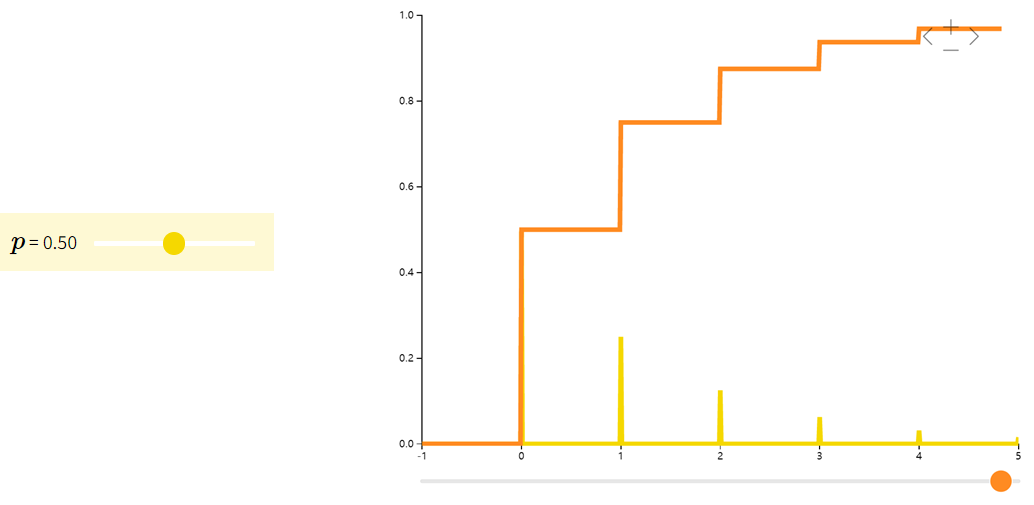
定义:指在伯努利试验中,试验r次才得到第一次成功的机率。即前r-1次都失败,在第r次成功的概率。
示例:射箭第几次能够正中靶心、有放回的情况下第几次能取到期望颜色的小球等等,求这种多次进行的试验下第几次能够达到想要的目的。
| PMF | 期望 | 方差 |
|---|---|---|
| f(x;p)=(1−p)xpf(x; p) = (1-p)^{x}pf(x;p)=(1−p)xp | 1p\frac{1}{p}p1 | 1−pp2\frac{1-p}{p^2}p21−p |
连续型随机变量
连续型随机变量可能取值的范围是一个无限不可数集合(如全体实数)。连续型随机变量的定义是:设 XXX 为随机变量,存在非负函数 f(x)f(x)f(x) 使得:
P(a≤X≤b)=∫abf(x)dxP(X<x)=F(x)P(a\leq X\leq b) =\int^b_a f(x) dx \\P(X< x) = F(x) P(a≤X≤b)=∫abf(x)dxP(X<x)=F(x)
概率密度函数 f(x)f(x)f(x): probability density function,PDF,是一个描述这个连续型随机变量的输出值,在某个确定的取值点附近的可能性的函数。概率密度函数如果满足以下两个性质则有效:
- ∀x∈Ω,f(x)≥0\forall x\in\Omega,f(x)\ge 0∀x∈Ω,f(x)≥0
- ∫−∞∞f(x)dx=1\int^{∞}_{-∞}f(x)dx=1∫−∞∞f(x)dx=1
均匀分布Uniform
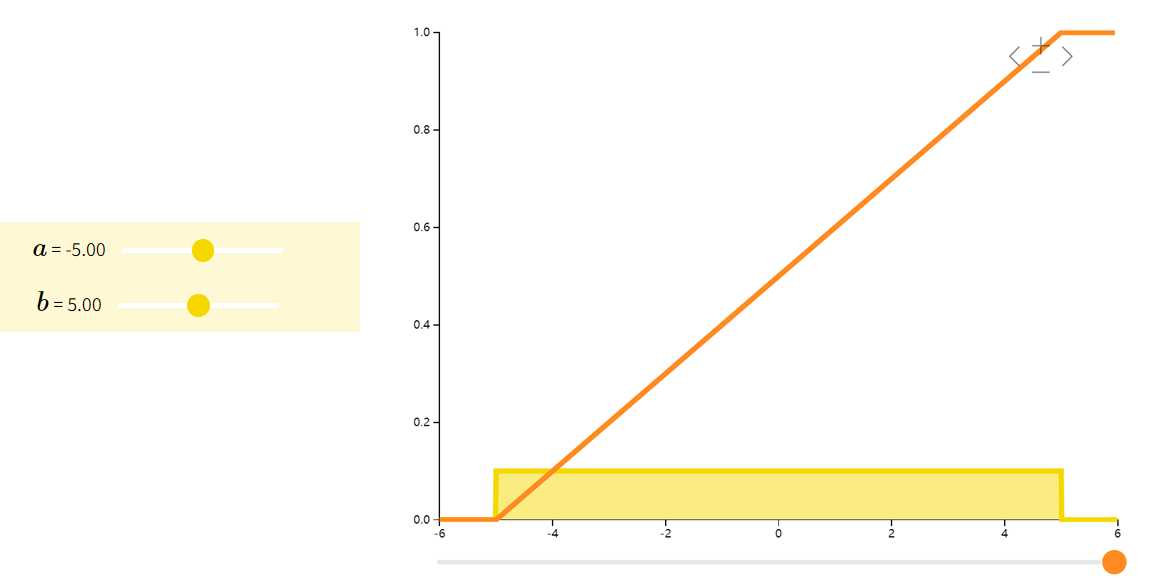
如果随机变量 XXX 在其支撑集上所有相同长度的区间上有相同的概率。即如果 b1−a1=b2−a2b_1-a_1 = b_2-a_2b1−a1=b2−a2 则有
P(X∈[a1,b1])=P(X∈[a2,b2])P(X\in [a_1,b_1])=P(X\in [a_2,b_2]) P(X∈[a1,b1])=P(X∈[a2,b2])
那么我们称 XXX 服从均匀分布(Uniform)。比方说,我们一般可以假设人在一年中出生的概率是相等的,因此可以用均匀分布来模拟人的出生时间。
| 期望 | 方差 | |
|---|---|---|
| f(x;a,b)={1b−afor x∈[a,b]0otherwise f(x;a,b) = \left\{\begin{array}{ll} \dfrac{1}{b-a} \text{ for } x \in [a,b]\\ 0 \qquad \text{ otherwise } \end{array}\right.f(x;a,b)={b−a1 for x∈[a,b]0 otherwise | a+b2\frac{a+b}{2}2a+b | (b−a)212\frac{(b-a)^2}{12}12(b−a)2 |
Gamma分布
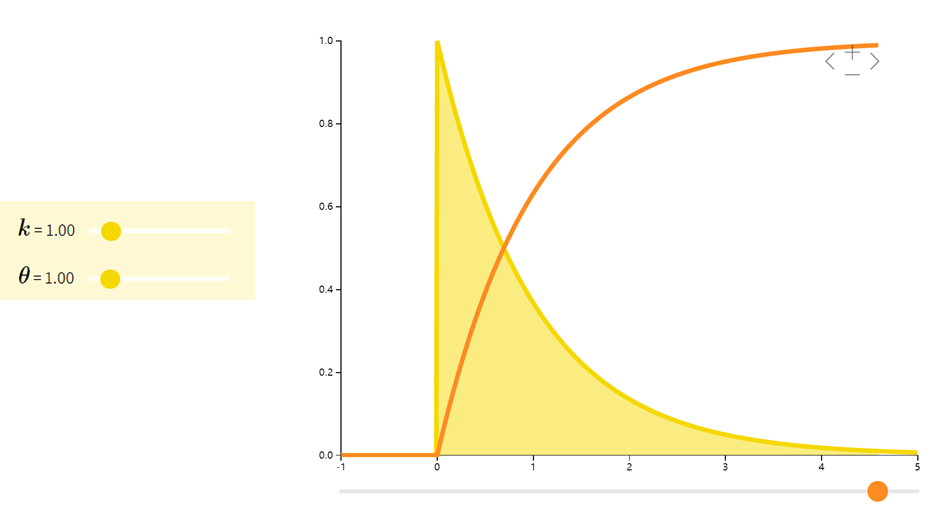
Gamma分布是一组连续型概率密度。指数分布和卡方分布是Gamma分布的两个特殊情形。
| 期望 | 方差 | |
|---|---|---|
| f(x;k,θ)=1Γ(k)θkxk−1e−xθf(x; k,\theta) = \dfrac{1}{\Gamma(k)\theta^{k}}x^{k-1}e^{-\dfrac{x}{\theta}}f(x;k,θ)=Γ(k)θk1xk−1e−θx | kθk\thetakθ | kθ2k\theta^2kθ2 |
伽玛函数(Gamma函数):Γ(x)=∫0+∞tx−1e−tdt(x>0)\Gamma(x)=\int_0^{+∞}t^{x-1} e^{-t}dt(x>0)Γ(x)=∫0+∞tx−1e−tdt(x>0),是阶乘在实数集上的延拓。
正态分布Normal
正态分布(也称高斯分布)的密度函数是一个钟形曲线。科学中常用正态分布来模拟许多小效应的叠加。比方说,我们知道人的身高是许多微小的基因和环境效应的叠加。因此可以用正态分布来表示人的身高。
| 期望 | 方差 | |
|---|---|---|
| f(x;μ,σ2)=12πσ2e−(x−μ)22σ2f(x;\mu, \sigma^2) = \dfrac{1}{\sqrt{2\pi\sigma^{2}}} e^{-\dfrac{(x-\mu)^{2}}{2\sigma^{2}}}f(x;μ,σ2)=2πσ21e−2σ2(x−μ)2 | μ\muμ | σ2\sigma^2σ2 |
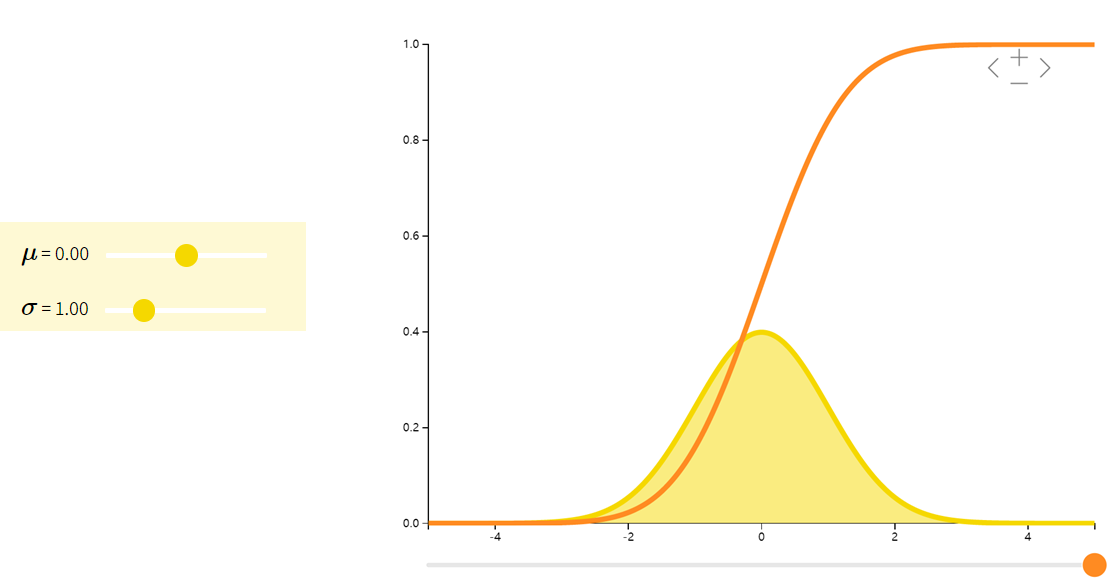
下面给出正态分布随机变量的一些有用的性质:
如果X∼N(μx,σx2),Y∼N(μy,σy2)X∼N(\mu_x,\sigma_x^2),Y∼N(\mu_y,\sigma_y^2)X∼N(μx,σx2),Y∼N(μy,σy2) 是独立的随机变量。则有:
(a) X+Y∼N(μx+μy,σx2+σy2)X+Y∼N(\mu_x+\mu_y,\sigma_x^2+\sigma_y^2)X+Y∼N(μx+μy,σx2+σy2)
(b) aX∼N(aμx,a2σx2)aX∼N(a\mu_x,a^2\sigma_x^2)aX∼N(aμx,a2σx2)
© X+a∼N(μx+a,σx2)X+a∼N(\mu_x+a,\sigma_x^2)X+a∼N(μx+a,σx2)
卡方分布Chi Squared
如果随机变量 XXX 是 kkk 个独立的标准正态随机变量的平方和,则称 XXX 为自由度是 kkk 的卡方随机变量:X∼χk2X\sim \chi_k^2X∼χk2。卡方分布常见于假设检验和构造置信区间。
| 期望 | 方差 | |
|---|---|---|
| ∑i=1kZi2Zi∼i.i.d.N(0,1)\sum_{i=1}^{k}Z_{i}^{2} \quad Z_{i} \overset{i.i.d.}{\sim} N(0,1)i=1∑kZi2Zi∼i.i.d.N(0,1) | kkk | 2k2k2k |
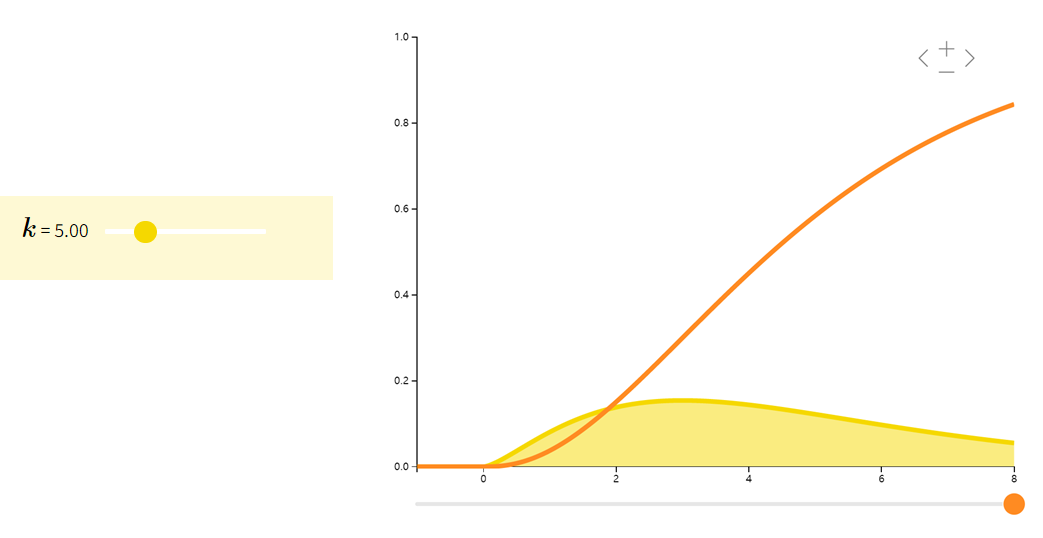
Student-t 分布
Student-t分布(也称t分布)往往在估计正态总体期望时出现。当我们只有较少的样本和未知的方差时,许多大样本性质并不适用,此时我们则需要用到t分布。
| 期望 | 方差 | |
|---|---|---|
| ZU/kZ∼N(0,1)U∼χk\dfrac{Z}{\sqrt{U/k}} \qquad \begin{array}{ll} Z \sim N(0,1)\\ U \sim \chi_{k} \end{array}U/kZZ∼N(0,1)U∼χk | 000 | kk−2\frac{k}{k-2}k−2k |
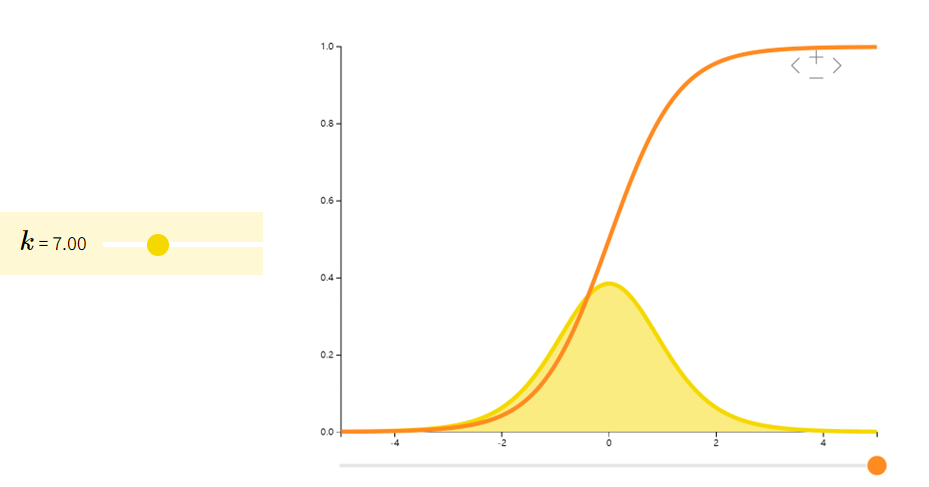
指数分布Exponential
指数分布可以看作是几何分布的连续版本,其常用于描述等待时间。具有无记忆性P(X>a+b∣X>a)=P(X>b)P(X>a+b|X>a)=P(X>b)P(X>a+b∣X>a)=P(X>b)。
| 期望 | 方差 | |
|---|---|---|
| (f(x;λ)={λe−λxif x≥00otherwise( f(x;\lambda) = \begin{cases} \lambda e^{-\lambda x} & \text{if } x \geq 0 \\ 0 & \text{otherwise} \end{cases}(f(x;λ)={λe−λx0if x≥0otherwise | 1λ\frac{1}{\lambda}λ1 | 1λ2\frac{1}{\lambda^2}λ21 |
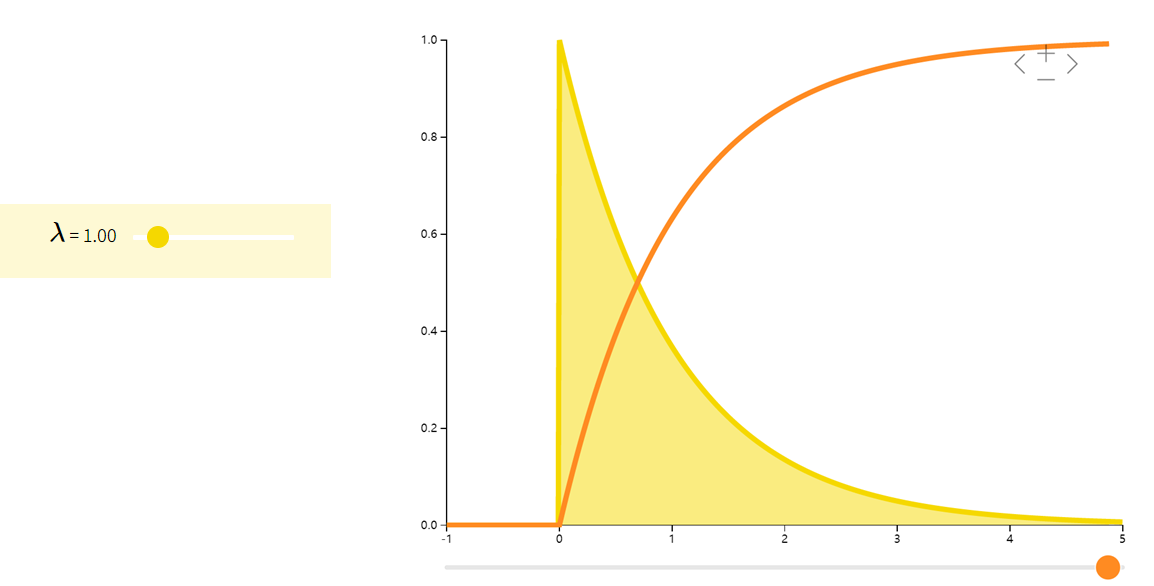
F分布Fisher–Snedecor
它是两个服从卡方分布的独立随机变量各除以其自由度后的比值的抽样分布,是一种非对称分布,且位置不可互换。F分布有着广泛的应用,如在方差分析、回归方程的显著性检验中都有着重要的地位。
| 期望 | 方差 | |
|---|---|---|
| U1/d1U2/d2U1∼χd1U2∼χd2\dfrac{U_{1}/d_{1}}{U_{2}/d_{2}} \quad \begin{array}{ll} U_{1} \sim \chi_{d_{1}}\\ U_{2} \sim \chi_{d_{2}} \end{array}U2/d2U1/d1U1∼χd1U2∼χd2 | d2d2−2\dfrac{d_{2}}{d_{2}-2}d2−2d2 | 2d22(d1+d2−2)d1(d2−2)2(d2−4)\dfrac{2d_{2}^{2}(d_{1} + d_{2} -2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}d1(d2−2)2(d2−4)2d22(d1+d2−2) |
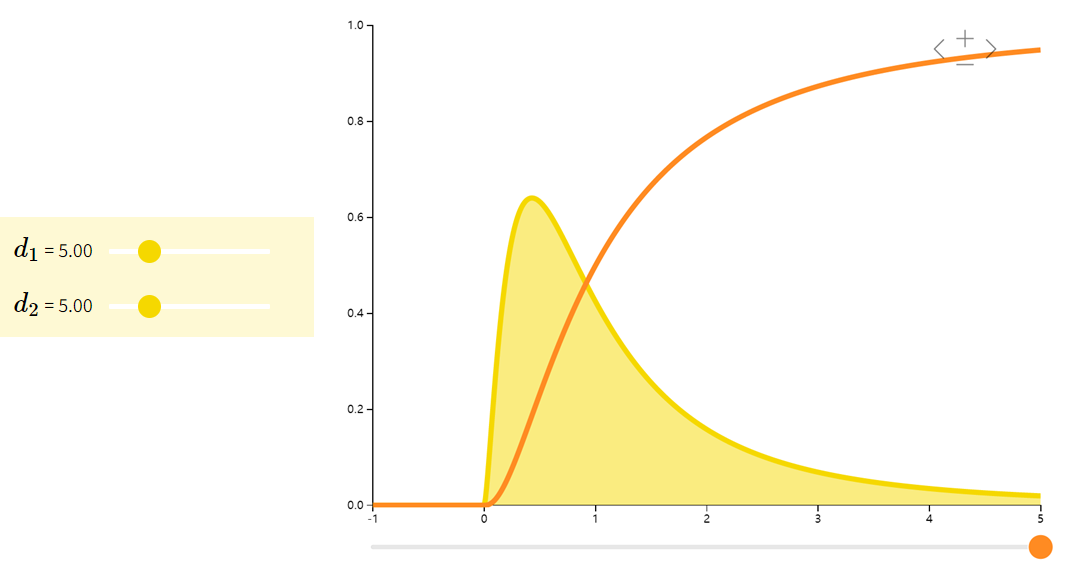
beta分布
Beta分布是一族在[0,1][0,1][0,1]上的连续型概率分布,常用于贝叶斯统计中的共轭先验分布。
| 期望 | 方差 | |
|---|---|---|
| f(x;α,β)=Γ(α+β)xα−1(1−x)β−1Γ(α)Γ(β)f(x;\alpha,\beta) = \dfrac{\Gamma(\alpha + \beta)x^{\alpha - 1}(1-x)^{\beta - 1}}{\Gamma(\alpha)\Gamma(\beta)}f(x;α,β)=Γ(α)Γ(β)Γ(α+β)xα−1(1−x)β−1 | αα+β\dfrac{\alpha}{\alpha + \beta}α+βα | αβ(α+β)2(α+β+1)\dfrac{\alpha\beta}{(\alpha + \beta)^{2}(\alpha + \beta + 1)}(α+β)2(α+β+1)αβ |
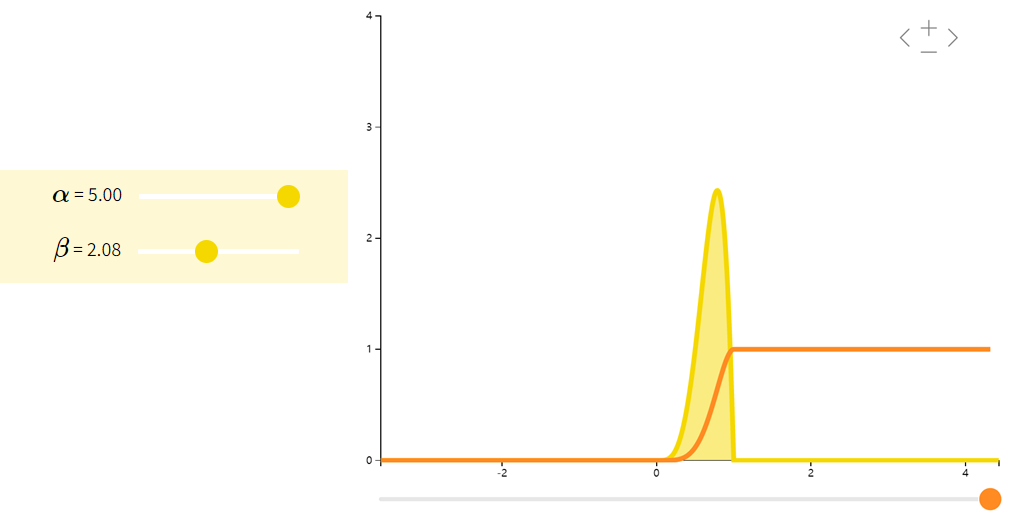
中心极限定理Central Limit Theorem
回到掷骰子的问题。假设你掷了50次骰子,并将平均掷出量记录X‾1=150∑k=150Xk\overline{X}_1=\frac{1}{50}\sum_{k=1}^{50}X_kX1=501∑k=150Xk。现在你重复这个实验,将平均掷出量记录为 X‾2\overline{X}_2X2。继续这样做,得到一连串的样本平均值 X‾1,X‾2,X‾3⋯\overline{X}_1,\overline{X}_2,\overline{X}_3\cdotsX1,X2,X3⋯。 如果你画出结果的直方图,你会开始注意到平均值 X‾i\overline{X}_iXi 的分布开始呈现正态。这个近似正态分布的平均值和方差是多少?它们应该与我们下面计算的 X‾i\overline{X}_iXi 的平均值和方差一致。请注意,这些计算并不取决于下标 iii,因为每个X‾i\overline{X}_iXi都是由50个独立的公平骰子掷出的样本平均值。因此,我们省略下标 iii,只是将样本平均值表示X‾=150∑k=150Xk\overline{X}=\frac{1}{50}\sum_{k=1}^{50}X_kX=501∑k=150Xk。
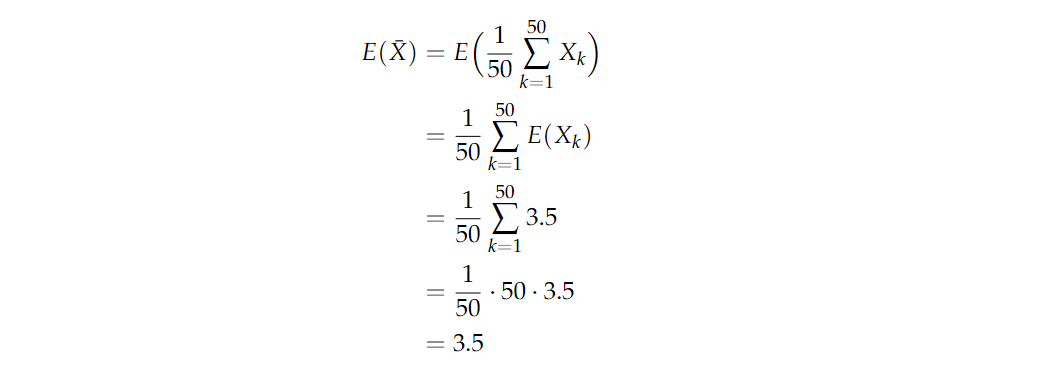
其中掷骰子的期望值为3.5,方差约为2.92。方差计算如下:

所以我们会开始观察到,样本平均数的序列开始类似于期望 μ=3.5μ=3.5μ=3.5 ,方差 σ2=0.0582σ^2=0.0582σ2=0.0582的正态分布。这个结果是由中心极限定理得出的,该定理陈述如下。
📏 定理:中心极限定理(Central Limit Theorem):让X1,X2,X3,⋯X_1,X_2,X_3,\cdotsX1,X2,X3,⋯是独立同分布的,平均值为μ\muμ ,方差为σ2\sigma^2σ2。则有:
X‾→N(μ,σ2n)\overline{X}\to N(\mu,\frac{\sigma^2}{n}) X→N(μ,nσ2)
n→∞n→∞n→∞。
这个定理的意思是,随着样本数量 nnn 的增加,样本均值 X‾\overline{X}X 的独立观测值看起来就像是从具有均值 μμμ 和方差 σ2\sigma^2σ2 的正态分布中提取出来的然而,这一结果对于XiX_iXi 的任何潜在分布都是正确的
📐 推论:中心极限定理的另一种写法为:
X‾−μσ/n→N(0,1)\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\to N(0,1) σ/nX−μ→N(0,1)
也说明,当n很大时,随机变量
Yn=∑i=1nXi−nμnσY_n = \frac{\sum_{i=1}^nX_i-n\mu}{\sqrt{n}\sigma} Yn=nσ∑i=1nXi−nμ
近似地服从标准正态分布N(0,1)N(0,1)N(0,1)。因此,当n很大时,
∑i=1nXi=nσYn+nμ\sum_{i=1}^{n}X_i=\sqrt{n}\sigma Y_n + n\mu i=1∑nXi=nσYn+nμ
近似地服从正态分布N(nμ,nσ2)N(nμ,nσ^2)N(nμ,nσ2)。该定理是中心极限定理最简单又最常用的一种形式,在实际工作中,只要n足够大,便可以把独立同分布的随机变量之和当作正态变量。这种方法在数理统计中用得很普遍,当处理大样本时,它是重要工具。
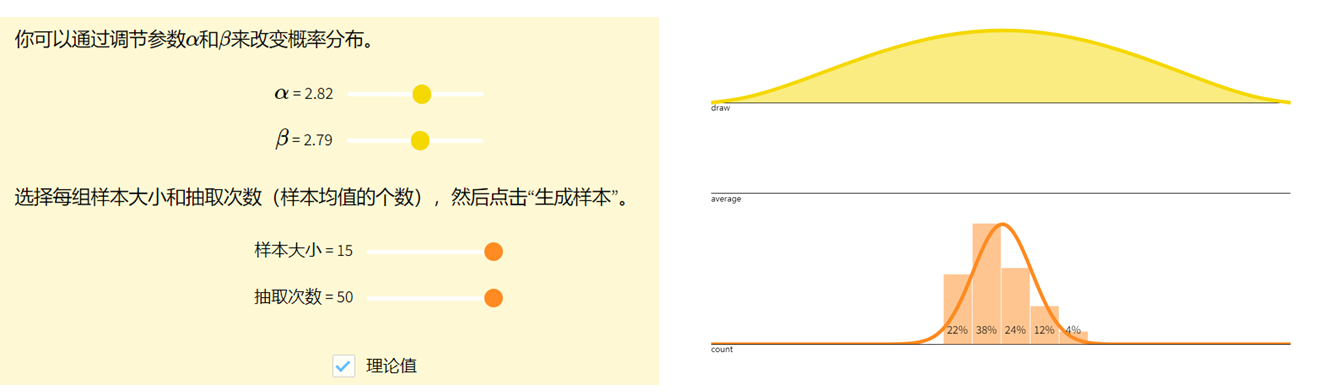
图示
中心极限定理告诉我们,对于一个(性质比较好的)分布,如果我们有足够大的独立同分布的样本,其样本均值会(近似地)呈正态分布。样本数量越大,其分布与正态越接近。
相关文章:

看见统计——第三章 概率分布
看见统计——第三章 概率分布 参考 https://github.com/seeingtheory/Seeing-Theory中心极限定理 概率分布描述了随机变量取值的规律。 随机变量Random Variables 🔥 定义:将样本空间中的结果映射到实数的函数 XXX 称为随机变量(random variable)&a…...
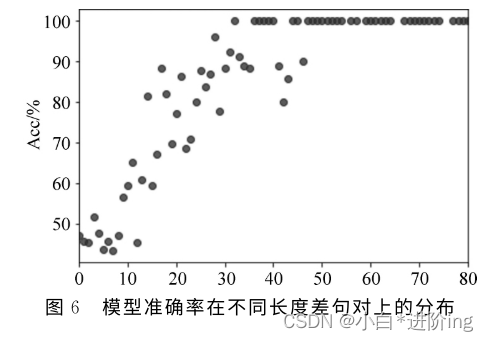
【基于众包标注的语文教材句子难易度评估研究 论文精读】
基于众包标注的语文教材句子难易度评估研究 论文精读信息摘 要0 引言1 相关研究2 众包标注方法3 语料库构建3.1 数据收集3.1 基于五点量表的专家标注3.3 基于成对比较的众包标注4 特征及模型4.1 特征抽取4.2 模型与实验设计4.2.1 任务一:单句绝对难度评估4.2.2 任务二:句对相对…...
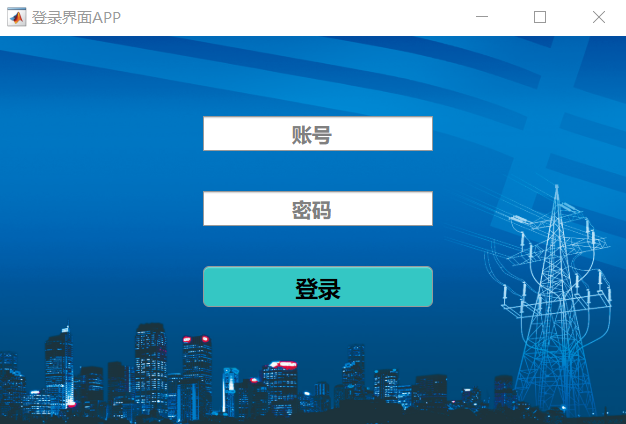
实例五:MATLAB APP design-APP登录界面的设计
一、APP 界面设计展示 注:在账号和密码提示框输入相应的账号和密码后,点击登录按钮,即可跳转到程序中设计的工作界面。 二、APP设计界面运行结果展示...

作用域和闭包:
1、LHS和RHS查询编译一段代码,需要js引擎和编译器(js引擎负责整个程序运行时所需的各种资源的调度,编译器只是js引擎的一部分,负责将JavaScript源码编译成机器能识别的机器指令,然后交给引擎运行)编译的过程…...

Vue常见面试题?
1、说说你对SPA单页面的理解,它的优缺点是什么? SPA(single-page application)仅在Web页面初始化时加载相应的HTML、JavaScript和CSS。一旦页面加载完成,SPA不会因为用户的操作而进行页面的重新加载或跳转;取而代之的是利用路由机…...
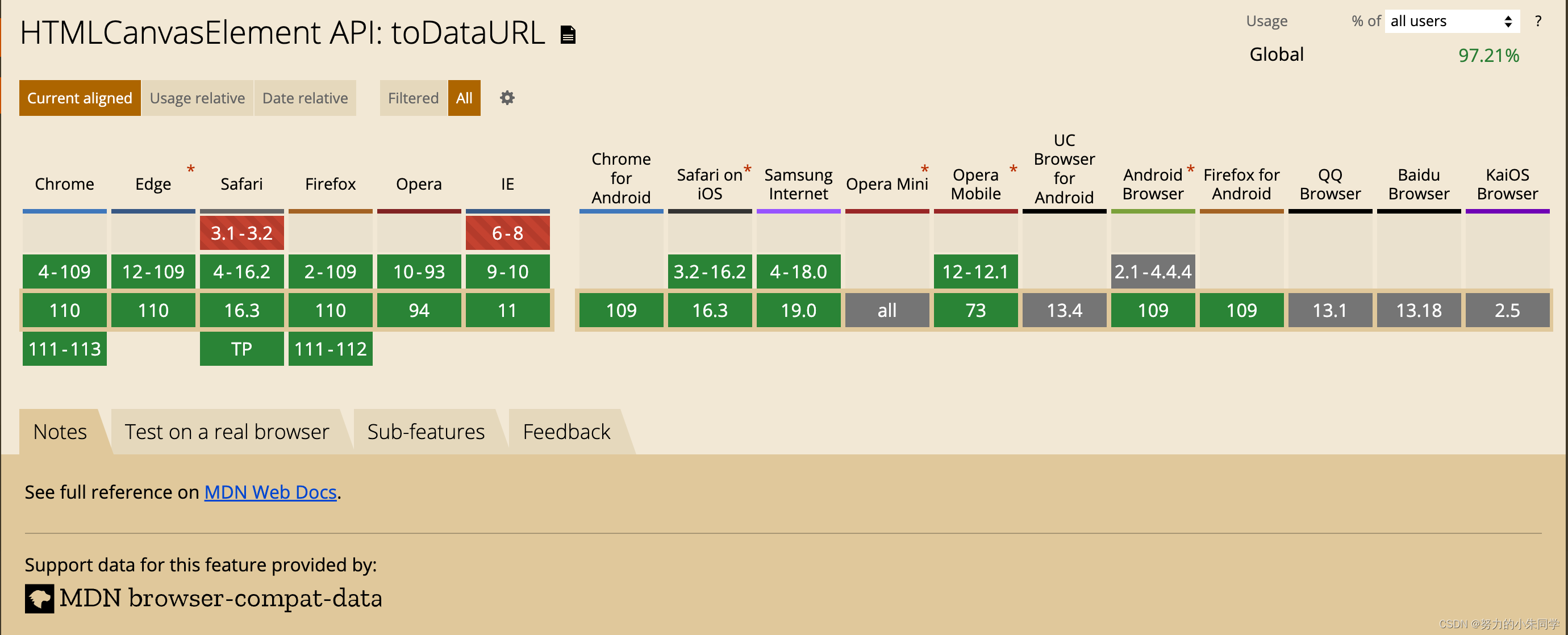
前端借助Canvas实现压缩图片两种方法
一、具体代码 1、利用canvas压缩图片方法一 // 第一种压缩图片方法(图片base64,图片类型,压缩比例,回调函数)// 图片类型是指 image/png、image/jpeg、image/webp(仅Chrome支持)// 该方法对以上三种图片类型都适用 压缩结果的图片base64与原类型相同// …...
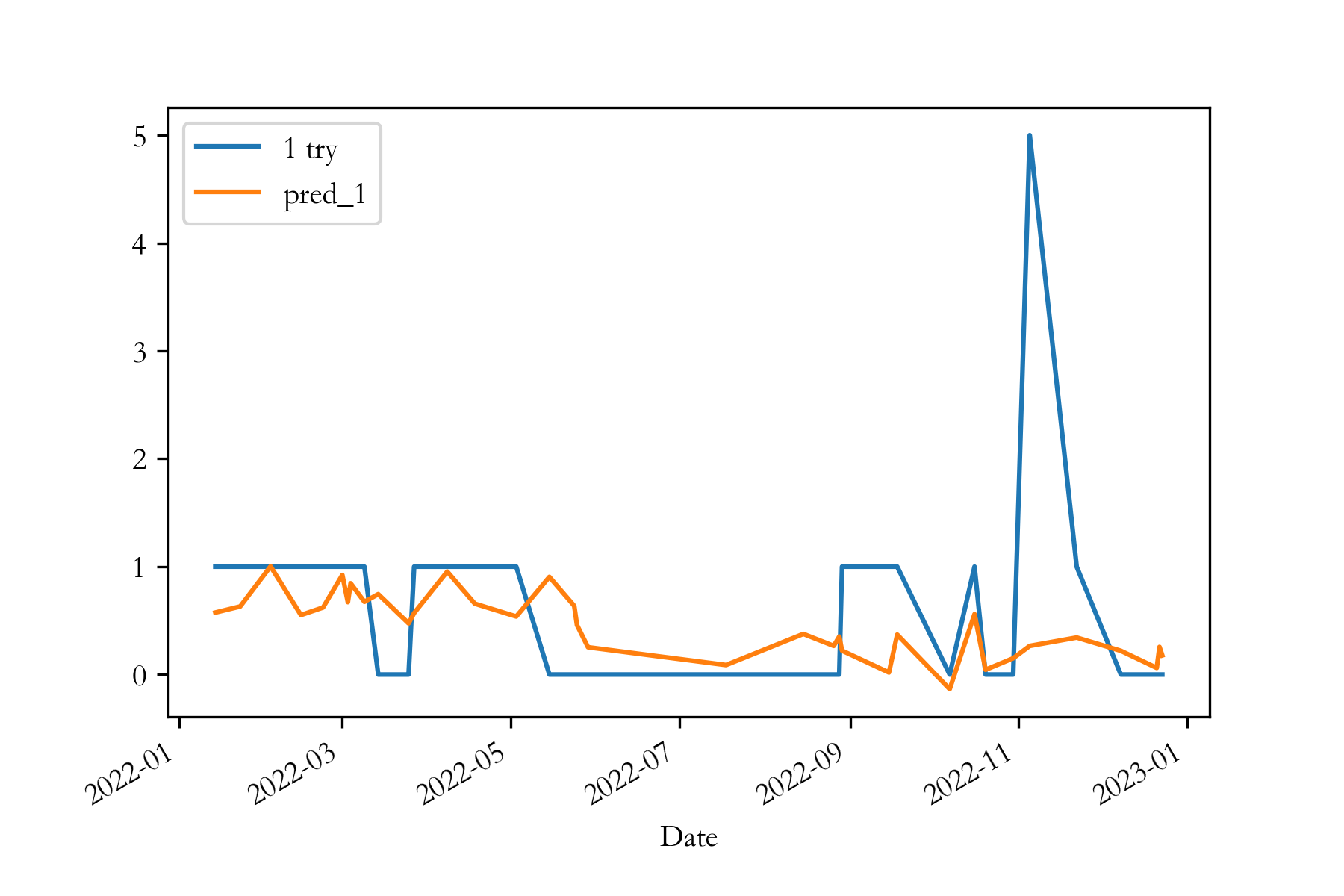
2023年美赛C题Wordle预测问题二建模及Python代码详细讲解
更新时间:2023-2-19 相关链接 (1)2023年美赛C题Wordle预测问题一建模及Python代码详细讲解 (2)2023年美赛C题Wordle预测问题二建模及Python代码详细讲解 (3)2023年美赛C题Wordle预测问题三、四…...

【算法】双指针
作者:指针不指南吗 专栏:算法篇 🐾或许会很慢,但是不可以停下来🐾 文章目录1.双指针分类2.双指针思想3.双指针应用1.双指针分类 常见问题分类 (1) 对于一个序列,用两个指针维护一段区间, 比如快速排序。 …...

Flutter-Widget-学习笔记
Widget 是整个视图描述的基础。 参考:https://docs.flutter.dev/resources/architectural-overview Widget 到底是什么呢? Widget 是 Flutter 功能的抽象描述,是视图的配置信息,同样也是数据的映射,是 Flutter 开发框…...

easyExcel 写复杂表头
写模板 模板图片: 实体类(这里没有用Data 是因为Lombok和easyExcal的版本冲突,在导入读取的时候获取不到值) package cn.iocoder.yudao.module.project.controller.admin.goods.vo;import com.alibaba.excel.annotation.ExcelI…...

关于线程池的执行流程和拒绝策略
使用线程池的好处为: 降低资源消耗:减少线程的创建和销毁带来的性能开销。 提高响应速度:当任务来时可以直接使用,不用等待线程创建 可管理性: 进行统一的分配,监控,避免大量的线程间因互相抢…...

【李忍考研传】二、约定
因为收学生证用了好些时间,李忍把学生证都交给班长后,就赶忙跑去食堂。远远地,他就看到那个瘦小的身影立在食堂正门前,那是他们约定每天午餐集合的地方。 “你咋这么慢啊……” “害!帮班长收东西耽误了点时间&#…...

2023-2-19 刷题情况
修改两个元素的最小分数 题目描述 给你一个下标从 0 开始的整数数组 nums 。 nums 的 最小 得分是满足 0 < i < j < nums.length 的 |nums[i] - nums[j]| 的最小值。nums的 最大 得分是满足 0 < i < j < nums.length 的 |nums[i] - nums[j]| 的最大值。nu…...

LeetCode笔记:Weekly Contest 333
LeetCode笔记:Weekly Contest 333 1. 题目一 1. 解题思路2. 代码实现 2. 题目二 1. 解题思路2. 代码实现 3. 题目三 1. 解题思路2. 代码实现 4. 题目四 比赛链接:https://leetcode.com/contest/weekly-contest-333 1. 题目一 给出题目一的试题链接如下…...

元数据管理 1
1、关于元数据管理原则说法正确的是 (知识点: 三月份模拟题)A.确保员工了解如何访问和使用元数据。B.制定、实施和审核元数据标准,以简化元数据的集成和使用。C.创建反馈机制,以便数据使用者可以将错误或过时的元数据反馈给元数据管理团队。D.以上都对正…...

统计二进制中比特1的个数
快速统计比特1的数量int CountBitOnes(int32_t n) {int result 0;for(;n;result) {n & n-1;}return result; }原理很简单,n-1会将n中最靠近结尾的1减一,这样n&n-1,n中最靠近结尾的1就变成了0;假设n 0b xxxxxxxx100n - 1…...

第三方实现跑马灯和手写实现跑马灯
目录第三方实现跑马灯手写实现跑马灯手写实现跑马灯【整体代码】自己细心研究一下上述代码第三方实现跑马灯 https://vue3-marquee.vercel.app/guide.html#changes-from-v2https://evodiaaut.github.io/vue-marquee-text-component/ 手写实现跑马灯 CSS部分 <style>.m…...
React Native Cannot run program “node“问题
概述 前几天mac重装系统了,用Android studio重新构建React native项目时,报Cannot run program "node"错误。 电脑系统为macOS 12.6.3 (Monterey),M1 Pro芯片。设备信息如下图所示: 完整错误信息如下图所示ÿ…...

python基于vue微信小程序 房屋租赁出租系统
目录 1 绪论 1 1.1课题背景 1 1.2课题研究现状 1 1.3初步设计方法与实施方案 2 1.4本文研究内容 2 2 系统开发环境 4 2.1 2.2MyEclipse环境配置 4 2.3 B/S结构简介 4 2.4MySQL数据库 5 2. 3 系统分析 6 3.1系统可行性分析 6 3.1.1经济可行性 6 3.1.2技术可行性 6 3.1.3运行可行…...

ThreadPoolExecutor管理异步线程笔记
为什么使用线程池? 线程的创建和销毁都需要不小的系统开销,不加以控制管理容易发生OOM错误。避免线程并发抢占系统资源导致系统阻塞。具备一定的线程管理能力(数量、存活时间,任务管理) new ThreadPoolExecutor(int …...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...
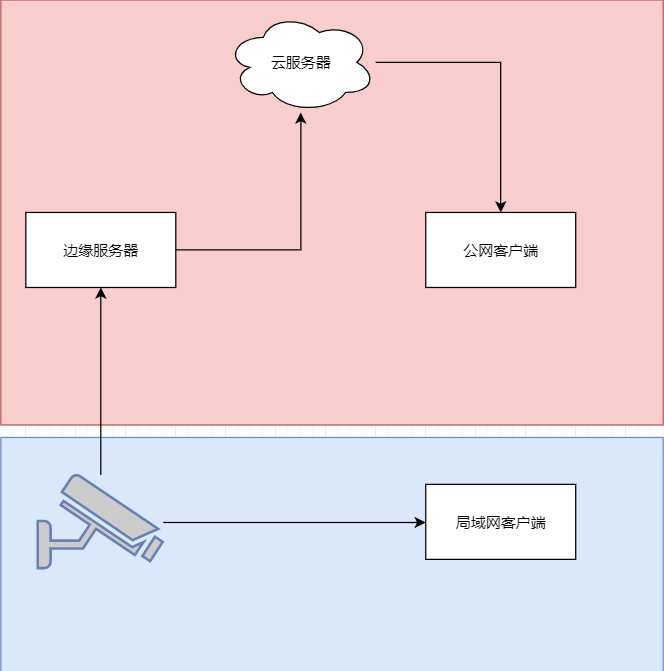
java 局域网 rtsp 取流 WebSocket 推送到前端显示 低延迟
众所周知 摄像头取流推流显示前端延迟大 传统方法是服务器取摄像头的rtsp流 然后客户端连服务器 中转多了,延迟一定不小。 假设相机没有专网 公网 1相机自带推流 直接推送到云服务器 然后客户端拉去 2相机只有rtsp ,边缘服务器拉流推送到云服务器 …...

Java多线程从入门到精通
一、基础概念 1.1 进程与线程 进程是指运行中的程序。 比如我们使用浏览器,需要启动这个程序,操作系统会给这个程序分配一定的资源(占用内存资源)。 线程是CPU调度的基本单位,每个线程执行的都是某一个进程的代码的某…...

浏览器工作原理01 [#]Chrome架构:仅仅打开了1个页面,为什么有4个进程
引用 浏览器工作原理与实践 Chrome打开一个页面需要启动多少进程?你可以点击Chrome浏览器右上角的“选项”菜单,选择“更多工具”子菜单,点击“任务管理器”,这将打开Chrome的任务管理器的窗口,如下图 和Windows任务管…...

HTMLCSS 学习总结
目录 一、HTML核心概念 三大前端技术作用 HTML基础结构 开发工具:VS Code 专业配置安装步骤: 二、HTML标签大全(含表格) 三、CSS核心技术 1. 三种引入方式对比 2.…...
