Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC)
Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC)
文章目录
- Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC)
- 1. 理论基础
- 1.1 Maximum Entropy Reinforcement Learning, MERL
- 1.2 Soft Policy Evaluation and Soft Policy Improvement in SAC
- 1.3 Two Q Value Neural Network
- 1.4 Tricks
- 1.5 Pesudocode
- 2. 代码实现
- 2.1 SAC处理连续动作空间
- 2.2 SAC处理离散动作空间
- Reference
Soft actor-critic方法又被称为Off-policy maximum entropy actor-critic algorithm。
1. 理论基础
1.1 Maximum Entropy Reinforcement Learning, MERL
在MERL原论文中,引入了熵的概念,熵定义如下:
随机变量 x x x符合 P P P的概率分布,那么随机变量 x x x的熵 H ( P ) \mathcal{H}(P) H(P)为
H ( P ) = E x ∼ P [ − log p ( x ) ] \mathcal{H}(P)=\mathbb{E}_{x\sim P}[-\log p(x)] H(P)=Ex∼P[−logp(x)]
标准的RL算法的目标是能够找到最大化累计收益的策略
π std ∗ = arg max π ∑ t E ( s t , a t ) ∼ ρ π [ r ( s t , a t ) ] \pi^*_{\text{std}} = \arg \max_\pi \sum_t \mathbb{E}_{(s_t,a_t)\sim \rho_\pi}[r(s_t, a_t)] πstd∗=argπmaxt∑E(st,at)∼ρπ[r(st,at)]
引入了熵最大化的RL算法的目标是
π M E R L ∗ = arg max π ∑ t E ( s t , a t ) ∼ ρ π [ r ( s t , a t ) + α H ( π ( ⋅ ∣ s t ) ) ] \pi^*_{MERL} = \arg\max_\pi \sum_t \mathbb{E}_{(s_t,a_t)\sim\rho_\pi}[r(s_t,a_t) + \alpha \mathcal{H}(\pi(\cdot|s_t))] πMERL∗=argπmaxt∑E(st,at)∼ρπ[r(st,at)+αH(π(⋅∣st))]
其中, ρ π \rho_\pi ρπ表示在策略 π \pi π下状态空间对的概率分布, α \alpha α是温度系数,用于调节对熵的重视程度。
类似的,我们也可以在RL的动作值函数,和状态值函数中同样引入熵的概念。
标准的RL算法的值函数
standard Q function: Q π ( s , a ) = E s t , a t ∼ ρ π [ ∑ t = 0 ∞ γ t r ( s t , a t ) ∣ s 0 = s , a 0 = a ] standard V function: V π ( s ) = E s t , a t ∼ ρ π [ ∑ t = 0 ∞ γ t r ( s t , a t ) ∣ s 0 = s ] \begin{aligned} \text{standard Q function:} \quad Q^\pi(s,a) & = \mathbb{E}_{s_t,a_t\sim\rho_\pi}[\sum_{t=0}^\infty \gamma^t r(s_t,a_t)|s_0=s, a_0=a] \\ \text{standard V function:} \quad V^\pi(s) & =\mathbb{E}_{s_t,a_t\sim\rho_\pi}[\sum_{t=0}^\infty \gamma^t r(s_t,a_t)|s_0=s] \end{aligned} standard Q function:Qπ(s,a)standard V function:Vπ(s)=Est,at∼ρπ[t=0∑∞γtr(st,at)∣s0=s,a0=a]=Est,at∼ρπ[t=0∑∞γtr(st,at)∣s0=s]
根据MERL的目标函数,在值函数中引入熵的概念之后就获得了Soft Value Function, SVF
Soft Q function: Q soft π ( s , a ) = E s t , a t ∼ ρ π [ ∑ t = 0 ∞ γ t r ( s t , a t ) + α ∑ t = 1 ∞ γ t H ( π ( ⋅ ∣ s t ) ) ∣ s 0 = s , a 0 = a ] Soft V function: V soft π ( s ) = E s t , a t ∼ ρ π [ ∑ t = 0 ∞ γ t ( r ( s t , a t ) + α H ( π ( ⋅ ∣ s t ) ) ) ∣ s 0 = s ] \begin{aligned} \text{Soft Q function:} \quad Q_{\text{soft}}^\pi(s,a) & = \mathbb{E}_{s_t,a_t\sim\rho_\pi}[\sum_{t=0}^\infty \gamma^t r(s_t,a_t) + \alpha \sum_{t=1}^\infty\gamma^t\mathcal{H} (\pi(\cdot|s_t)) |s_0=s, a_0=a] \\ \text{Soft V function:} \quad V_{\text{soft}}^\pi(s) & =\mathbb{E}_{s_t,a_t\sim\rho_\pi}[\sum_{t=0}^\infty \gamma^t \Big( r(s_t,a_t) + \alpha \mathcal{H} (\pi(\cdot|s_t)) \Big)|s_0=s] \end{aligned} Soft Q function:Qsoftπ(s,a)Soft V function:Vsoftπ(s)=Est,at∼ρπ[t=0∑∞γtr(st,at)+αt=1∑∞γtH(π(⋅∣st))∣s0=s,a0=a]=Est,at∼ρπ[t=0∑∞γt(r(st,at)+αH(π(⋅∣st)))∣s0=s]
观察上式我们就可以获得Soft Bellman Equation
Q soft π ( s , a ) = E s ′ ∼ p ( s ′ ∣ s , a ) a ′ ∼ π [ r ( s , a ) + γ ( Q soft π ( s ′ , a ′ ) + α H ( π ( ⋅ ∣ s ′ ) ) ) ] = E s ′ ∼ p ( s ′ ∣ s , a ) [ r ( s , a ) + γ V soft π ( s ) ] \begin{aligned} Q_{\text{soft}}^\pi(s,a) & = \mathbb{E}_{s^\prime \sim p(s^\prime|s,a)\\ a^\prime\sim \pi}[r(s,a) + \gamma \Big( Q_{\text{soft}}^\pi(s^\prime,a^\prime) + \alpha \mathcal{H}(\pi(\cdot|s^\prime)) \Big)] \\ & = \mathbb{E}_{s^\prime\sim p(s^\prime|s,a)} [r(s,a) + \gamma V_{\text{soft}}^\pi(s)] \end{aligned} Qsoftπ(s,a)=Es′∼p(s′∣s,a)a′∼π[r(s,a)+γ(Qsoftπ(s′,a′)+αH(π(⋅∣s′)))]=Es′∼p(s′∣s,a)[r(s,a)+γVsoftπ(s)]
V soft π ( s ) = E s t , a t ∼ ρ π [ ∑ t = 0 ∞ γ t ( r ( s t , a t ) + α H ( π ( ⋅ ∣ s t ) ) ) ∣ s 0 = s ] = E s t , a t ∼ ρ π [ ∑ t = 0 ∞ γ t r ( s t , a t ) + α ∑ t = 1 ∞ γ t H ( π ( ⋅ ∣ s t ) ) + α H ( π ( ⋅ ∣ s t ) ∣ s 0 = s ] = E s t , a t ∼ ρ π [ Q soft π ( s , a ) ∣ s 0 = s , a 0 = a ] + α H ( π ( ⋅ ∣ s t ) ) = E a ∼ π [ Q soft π ( s , a ) − α log π ( a ∣ s ) ] \begin{aligned} V_{\text{soft}}^\pi(s) & = \mathbb{E}_{s_t,a_t\sim\rho_\pi}[\sum_{t=0}^\infty \gamma^t \Big( r(s_t,a_t) + \alpha \mathcal{H} (\pi(\cdot|s_t)) \Big)|s_0=s] \\ & = \mathbb{E}_{s_t,a_t\sim\rho_\pi}[\sum_{t=0}^\infty \gamma^t r(s_t,a_t) + \alpha \sum_{t=1}^\infty\gamma^t\mathcal{H} (\pi(\cdot|s_t)) + \alpha \mathcal{H}(\pi(\cdot|s_t)|s_0=s] \\ & = \mathbb{E}_{s_t,a_t\sim\rho_\pi}[Q_{\text{soft}}^\pi(s,a)|s_0=s,a_0=a] + \alpha \mathcal{H}(\pi(\cdot|s_t)) \\ & = \textcolor{blue}{\mathbb{E}_{a\sim\pi}[Q_{\text{soft}}^\pi(s,a) - \alpha \log \pi(a|s)]} \end{aligned} Vsoftπ(s)=Est,at∼ρπ[t=0∑∞γt(r(st,at)+αH(π(⋅∣st)))∣s0=s]=Est,at∼ρπ[t=0∑∞γtr(st,at)+αt=1∑∞γtH(π(⋅∣st))+αH(π(⋅∣st)∣s0=s]=Est,at∼ρπ[Qsoftπ(s,a)∣s0=s,a0=a]+αH(π(⋅∣st))=Ea∼π[Qsoftπ(s,a)−αlogπ(a∣s)]
1.2 Soft Policy Evaluation and Soft Policy Improvement in SAC
soft Q function的值迭代公式
Q soft π ( s , a ) = E s ′ ∼ p ( s ′ ∣ s , a ) a ′ ∼ π [ r ( s , a ) + γ ( Q soft π ( s ′ , a ′ ) + α H ( π ( ⋅ ∣ s ′ ) ) ) ] = E s ′ ∼ p ( s ′ ∣ s , a ) [ r ( s , a ) + γ V soft π ( s ) ] \begin{align} Q_{\text{soft}}^\pi(s,a) & = \mathbb{E}_{s^\prime \sim p(s^\prime|s,a)\\ a^\prime\sim \pi}[r(s,a) + \gamma \Big( Q_{\text{soft}}^\pi(s^\prime,a^\prime) + \alpha \mathcal{H}(\pi(\cdot|s^\prime)) \Big)] \tag{1.1} \\ & = \mathbb{E}_{s^\prime\sim p(s^\prime|s,a)} [r(s,a) + \gamma V_{\text{soft}}^\pi(s)] \tag{1.2} \end{align} Qsoftπ(s,a)=Es′∼p(s′∣s,a)a′∼π[r(s,a)+γ(Qsoftπ(s′,a′)+αH(π(⋅∣s′)))]=Es′∼p(s′∣s,a)[r(s,a)+γVsoftπ(s)](1.1)(1.2)
soft V function的值迭代公式
V soft π ( s ) = E a ∼ π [ Q soft π ( s , a ) − α log π ( a ∣ s ) ] (1.3) V_{\text{soft}}^\pi(s)= \mathbb{E}_{a\sim\pi}[Q_{\text{soft}}^\pi(s,a) - \alpha \log \pi(a|s)] \tag{1.3} Vsoftπ(s)=Ea∼π[Qsoftπ(s,a)−αlogπ(a∣s)](1.3)
在SAC中如果我们只打算维持一个Q值函数,那么使用式子 ( 1 , 1 ) (1,1) (1,1)进行值迭代即可,
如果需要同时维持Q,V两个函数,那么使用式子 ( 1 , 2 ) , ( 1 , 3 ) (1,2),(1,3) (1,2),(1,3)进行值迭代。
下面直接给出训练中的损失函数
V值函数的损失函数
J V ( ψ ) = E s t ∼ D [ 1 2 ( V ψ ( s t ) − E a t ∼ π ϕ [ Q θ ( s t , a t ) − log π ϕ ( a t ∣ s t ) ] ) 2 ] J_{V(\psi)} = \mathbb{E}_{s_t\sim\mathcal{D}} \Big[\frac{1}{2}(V_{\psi}(s_t) - \mathbb{E}_{a_t\sim\pi_{\phi}}[Q_\theta(s_t,a_t)- \log \pi_\phi(a_t|s_t)])^2 \Big] JV(ψ)=Est∼D[21(Vψ(st)−Eat∼πϕ[Qθ(st,at)−logπϕ(at∣st)])2]
Q值函数的损失函数
J Q ( θ ) = E ( s t , a t ) ∼ D [ 1 2 ( Q θ ( s t , a t ) − Q ^ ( s t , a t ) ) ] Q ^ ( s t , a t ) = r ( s t , a t ) + γ E s t + 1 ∼ p [ V ψ ( s t + 1 ) ] Q ^ ( s t , a t ) = r ( s t , a t ) + γ Q θ ( s t + 1 , a t + 1 ) J_{Q(\theta)} = \mathbb{E}_{(s_t,a_t)\sim\mathcal{D}} \Big[ \frac{1}{2}\Big( Q_\theta(s_t,a_t) - \hat{Q}(s_t,a_t) \Big) \Big] \\ \hat{Q}(s_t,a_t) = r(s_t,a_t) + \gamma \mathbb{E}_{s_{t+1}\sim p}[V_{\psi}(s_{t+1})] \\ \hat{Q}(s_t,a_t) = r(s_t,a_t) + \gamma Q_\theta(s_{t+1},a_{t+1}) JQ(θ)=E(st,at)∼D[21(Qθ(st,at)−Q^(st,at))]Q^(st,at)=r(st,at)+γEst+1∼p[Vψ(st+1)]Q^(st,at)=r(st,at)+γQθ(st+1,at+1)
策略 π \pi π的损失函数
J π ( ϕ ) = E s t ∼ D [ D K L ( π ϕ ( ⋅ ∣ s t ) ∣ ∣ exp ( Q θ ( s t , ⋅ ) ) Z θ ( s t ) ) ] J_\pi(\phi) = \mathbb{E}_{s_t\sim \mathcal{D}} \Big[ \mathbb{D}_{KL}\Big( \pi_\phi(\cdot|s_t) \big|\big| \frac{\exp(Q_\theta(s_t,\cdot))}{Z_\theta(s_t)} \Big) \Big] Jπ(ϕ)=Est∼D[DKL(πϕ(⋅∣st) Zθ(st)exp(Qθ(st,⋅)))]
其中, Z θ ( s t ) Z_\theta(s_t) Zθ(st)是分配函数 (partition function)
KL散度的定义如下
假设对随机变量 ξ \xi ξ,存在两个概率分布P和Q,其中P是真实的概率分布,Q是较容易获得的概率分布。如果 ξ \xi ξ是离散的随机变量,那么定义从P到Qd KL散度为
D K L ( P ∣ ∣ Q ) = ∑ i P ( i ) ln ( P ( i ) Q ( i ) ) \mathbb{D}_{KL}(P\big|\big|Q) = \sum_i P(i)\ln(\frac{P(i)}{Q(i)}) DKL(P Q)=i∑P(i)ln(Q(i)P(i))
如果 ξ \xi ξ是连续变量,则定义从P到Q的KL散度为
D K L ( P ∣ ∣ Q ) = ∫ − ∞ ∞ p ( x ) ln ( p ( x ) q ( x ) ) d x \mathbb{D}_{KL}(P\big|\big|Q) = \int^\infty_{-\infty}p(\mathbb{x})\ln(\frac{p(\mathbb{x})}{q(\mathbb{x})}) d\mathbb{x} DKL(P Q)=∫−∞∞p(x)ln(q(x)p(x))dx
那么根据离散的KL散度定义,我们可以将策略 π \pi π的损失函数展开如下
J π ( ϕ ) = E s t ∼ D [ D K L ( π ϕ ( ⋅ ∣ s t ) ∣ ∣ exp ( Q θ ( s t , ⋅ ) ) Z θ ( s t ) ) ] = E s t ∼ D [ ∑ π ϕ ( ⋅ ∣ s t ) ln ( π ϕ ( ⋅ ∣ s t ) Z θ ( s t ) exp ( Q θ ( s t , ⋅ ) ) ) ] = E s t ∼ D , a t ∼ π ϕ [ ln ( π ϕ ( ⋅ ∣ s t ) + ln ( Z θ ( s t ) ) − Q θ ( s t , ⋅ ) ] = E s t ∼ D , a t ∼ π ϕ [ ln ( π ϕ ( ⋅ ∣ s t ) ) − Q θ ( s t , ⋅ ) ] \begin{align} J_\pi(\phi) & = \mathbb{E}_{s_t\sim \mathcal{D}} \Big[ \mathbb{D}_{KL}\Big( \pi_\phi(\cdot|s_t) \big|\big| \frac{\exp(Q_\theta(s_t,\cdot))}{Z_\theta(s_t)} \Big) \Big] \\ & = \mathbb{E}_{s_t\sim\mathcal{D}} \Big[ \sum\pi_\phi(\cdot|s_t) \ln(\frac{\pi_\phi(\cdot|s_t)Z_\theta(s_t)}{\exp(Q_\theta(s_t,\cdot))}) \Big] \\ & = \mathbb{E}_{s_t\sim\mathcal{D}, a_t\sim \pi_\phi} \Big[ \ln(\pi_\phi(\cdot|s_t) + \ln(Z_\theta(s_t)) - Q_\theta(s_t,\cdot) \Big] \\ & = \textcolor{blue}{\mathbb{E}_{s_t\sim\mathcal{D}, a_t\sim \pi_\phi} \Big[ \ln(\pi_\phi(\cdot|s_t)) - Q_\theta(s_t,\cdot) \Big]} \tag{1.4} \end{align} Jπ(ϕ)=Est∼D[DKL(πϕ(⋅∣st) Zθ(st)exp(Qθ(st,⋅)))]=Est∼D[∑πϕ(⋅∣st)ln(exp(Qθ(st,⋅))πϕ(⋅∣st)Zθ(st))]=Est∼D,at∼πϕ[ln(πϕ(⋅∣st)+ln(Zθ(st))−Qθ(st,⋅)]=Est∼D,at∼πϕ[ln(πϕ(⋅∣st))−Qθ(st,⋅)](1.4)
最后一步是因为,分配函数 Z θ Z_\theta Zθ与策略 π \pi π无关,所以对梯度没有影响,所以在目标函数中可以直接忽略。
然后又引入了 reparameter的方法,
a t = f ϕ ( ϵ t ; s t ) , ϵ ∼ N a_t = f_\phi(\epsilon_t;s_t), \epsilon\sim\mathcal{N} at=fϕ(ϵt;st),ϵ∼N
将上式带入 ( 1.4 ) (1.4) (1.4)中则有
J π ( ϕ ) = E s t ∼ D , a t ∼ π ϕ [ ln ( π ϕ ( f ϕ ( ϵ t ; s t ) ∣ s t ) ) − Q θ ( s t , f ϕ ( ϵ t ; s t ) ) ] J_\pi(\phi)=\mathbb{E}_{s_t\sim\mathcal{D}, a_t\sim \pi_\phi} \Big[ \ln\Big(\pi_\phi\big(f_\phi(\epsilon_t;s_t)|s_t\big)\Big) - Q_\theta\Big(s_t,f_\phi(\epsilon_t;s_t)\Big) \Big] Jπ(ϕ)=Est∼D,at∼πϕ[ln(πϕ(fϕ(ϵt;st)∣st))−Qθ(st,fϕ(ϵt;st))]
最后,只需要不断收集数据,缩小这两个损失函数,就可以得到收敛到一个解。
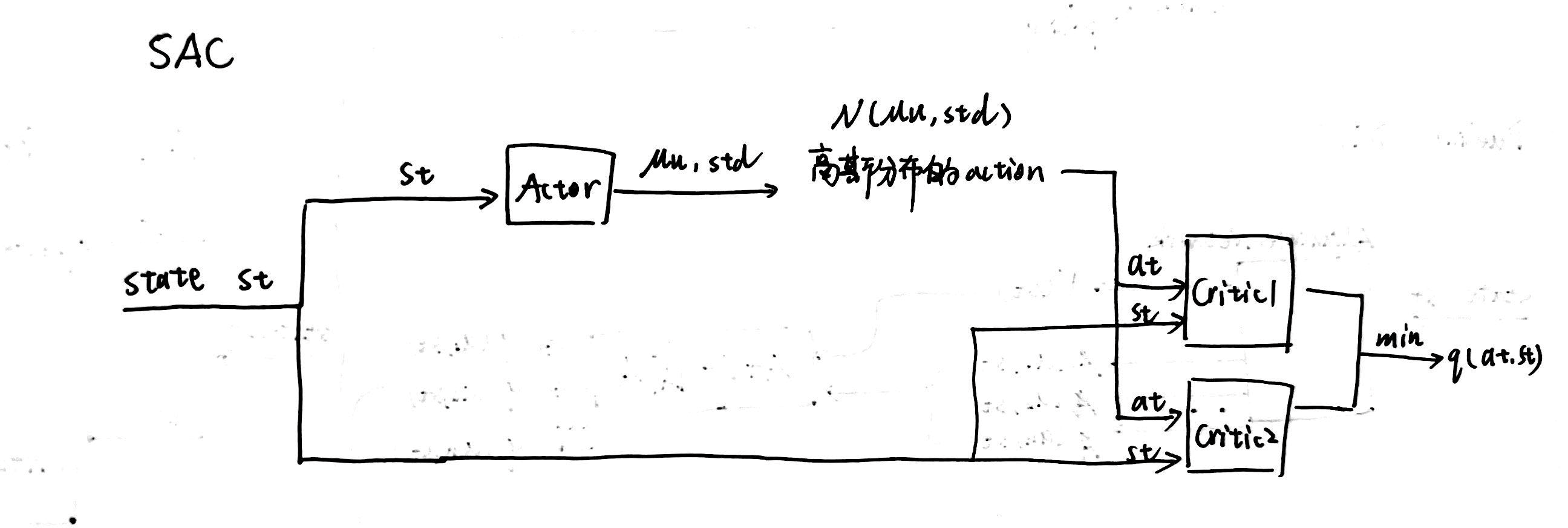
1.3 Two Q Value Neural Network
SAC的策略网络与DDPG中策略网络直接估计动作值大小不同,SAC的策略网络是估计连续动作空间Gaussian分布的均值和方差,再从这个Gaussian 分布中均匀采样获得连续的动作值。SAC中可以维护一个V值函数网络,也可以不维护V值函数网络,但是SAC中必须的是两个Q值函数网络及两个Q值网络的target network和一个策略网络 π \pi π。为什么要维护两个Q值网络呢?这是因为为了减少Q值网络存在的过高估计的问题。然后用两个Q值网络中较小的Q值网络来计算损失函数,假设存在两个Q值网络 Q ( θ 1 ) , Q ( θ 2 ) Q(\theta_1),Q(\theta_2) Q(θ1),Q(θ2)和其对应的target network Q ( θ 1 − ) , Q ( θ 2 − ) Q(\theta_1^-),Q(\theta_2^-) Q(θ1−),Q(θ2−)
那么Q值函数的损失函数就成了
J Q ( θ ) = E ( s t , a t ) ∼ D [ 1 2 ( Q θ ( s t , a t ) − Q ^ ( s t , a t ) ) ] Q ^ ( s t , a t ) = r ( s t , a t ) + γ V ψ ( s t + 1 ) V ψ ( s t + 1 ) = Q θ ( s t + 1 , a t + 1 ) − α log ( π ( a t + 1 ∣ s t + 1 ) ) \begin{align} J_Q(\theta) & = \mathbb{E}_{(s_t,a_t)\sim\mathcal{D}} \Big[ \frac{1}{2}\Big( Q_\theta(s_t,a_t) - \hat{Q}(s_t,a_t) \Big) \Big] \tag{1.5} \\ \hat{Q}(s_t,a_t) & = r(s_t,a_t) + \gamma V_\psi(s_{t+1}) \tag{1.6} \\ V_\psi(s_{t+1}) & = Q_\theta(s_{t+1}, a_{t+1}) - \alpha \log (\pi(a_{t+1}|s_{t+1})) \tag{1.7} \end{align} JQ(θ)Q^(st,at)Vψ(st+1)=E(st,at)∼D[21(Qθ(st,at)−Q^(st,at))]=r(st,at)+γVψ(st+1)=Qθ(st+1,at+1)−αlog(π(at+1∣st+1))(1.5)(1.6)(1.7)
结合式子 1.5 , 1.6 , 1.7 1.5, 1.6, 1.7 1.5,1.6,1.7则有
J Q ( θ ) = E ( s t , a t ) ∼ D [ 1 2 ( Q θ ( s t , a t ) − ( r ( s t , a t ) + γ ( min j = 1 , 2 Q θ j − ( s t + 1 , a t + 1 ) − α log π ( a t + 1 ∣ s t + 1 ) ) ) ) 2 ] J_Q(\theta) = \textcolor{red}{\mathbb{E}_{(s_t,a_t)\sim\mathcal{D}} \Big[ \frac{1}{2}\Big( Q_\theta(s_t,a_t) - \Big(r(s_t,a_t)+\gamma \big(\min_{j=1,2}Q_{\theta_j^-}(s_{t+1},a_{t+1}) - \alpha \log\pi(a_{t+1}|s_{t+1}) \big) \Big) \Big)^2 \Big]} JQ(θ)=E(st,at)∼D[21(Qθ(st,at)−(r(st,at)+γ(j=1,2minQθj−(st+1,at+1)−αlogπ(at+1∣st+1))))2]
因为SAC也是一种离线的算法,为了让训练更加稳定,这里使用了目标Q网络 Q ( θ − ) Q(\theta^-) Q(θ−),同样是两个目标网络,与两个Q网络相对应,SAC中目标Q网络的更新方式和DDPG中一致。
之前推导了策略 π ( ϕ ) \pi(\phi) π(ϕ)的损失函数如下
J π ( ϕ ) = E s t ∼ D , a t ∼ π ϕ [ ln ( π ϕ ( ⋅ ∣ s t ) ) − Q θ ( s t , ⋅ ) ] J_\pi(\phi) = \mathbb{E}_{s_t\sim\mathcal{D}, a_t\sim \pi_\phi} \Big[ \ln(\pi_\phi(\cdot|s_t)) - Q_\theta(s_t,\cdot) \Big] Jπ(ϕ)=Est∼D,at∼πϕ[ln(πϕ(⋅∣st))−Qθ(st,⋅)]
再引入reparameter化简之后,就成了
J π ( ϕ ) = E s t ∼ D , a t ∼ π ϕ [ ln ( π ϕ ( f ϕ ( ϵ t ; s t ) ∣ s t ) ) − Q θ ( s t , f ϕ ( ϵ t ; s t ) ) ] J_\pi(\phi)=\mathbb{E}_{s_t\sim\mathcal{D}, a_t\sim \pi_\phi} \Big[ \ln\Big(\pi_\phi\big(f_\phi(\epsilon_t;s_t)|s_t\big)\Big) - Q_\theta\Big(s_t,f_\phi(\epsilon_t;s_t)\Big) \Big] Jπ(ϕ)=Est∼D,at∼πϕ[ln(πϕ(fϕ(ϵt;st)∣st))−Qθ(st,fϕ(ϵt;st))]
利用双Q网络取最小,再将上述目标函数进行改写
J π ( ϕ ) = E s t ∼ D , a t ∼ π ϕ [ ln ( π ϕ ( f ϕ ( ϵ t ; s t ) ∣ s t ) ) − min j = 1 , 2 Q θ j ( s t , f ϕ ( ϵ t ; s t ) ) ] J_\pi(\phi)= \textcolor{red}{\mathbb{E}_{s_t\sim\mathcal{D}, a_t\sim \pi_\phi} \Big[ \ln\Big(\pi_\phi\big(f_\phi(\epsilon_t;s_t)|s_t\big)\Big) - \min_{j=1,2}Q_{\theta_j}\Big(s_t,f_\phi(\epsilon_t;s_t)\Big) \Big]} Jπ(ϕ)=Est∼D,at∼πϕ[ln(πϕ(fϕ(ϵt;st)∣st))−j=1,2minQθj(st,fϕ(ϵt;st))]
1.4 Tricks
SAC还集成了一些别的算法的常用技巧,比如Replay Buffer来产生independent and identically distribution的样本,使用了Double DQN中target network的思想使用两个网络。SAC中最重要的一个技巧是自动调整熵正则项,在 SAC 算法中,如何选择熵正则项的系数非常重要。在不同的状态下需要不同大小的熵:在最优动作不确定的某个状态下,熵的取值应该大一点;而在某个最优动作比较确定的状态下,熵的取值可以小一点。为了自动调整熵正则项,SAC 将强化学习的目标改写为一个带约束的优化问题:
max π E π [ ∑ t r ( s t , a t ) ] s.t. E ( s t , a t ) ∼ ρ π [ − log ( π t ( a t ∣ s t ) ) ] ≥ H 0 \max_\pi \mathbb{E}_\pi\Big[ \sum_t r(s_t,a_t) \Big] \quad \text{s.t.} \quad \mathbb{E}_{(s_t,a_t)\sim\rho_\pi}[-\log (\pi_t(a_t|s_t))] \ge \mathcal{H}_0 πmaxEπ[t∑r(st,at)]s.t.E(st,at)∼ρπ[−log(πt(at∣st))]≥H0
H 0 \mathcal{H}_0 H0 是预先定义好的最小策略熵的阈值。通过一些数学技巧简化,可以得到温度 α \alpha α的损失函数
J ( α ) = E s t ∼ R , a t ∼ π ( ⋅ ∣ s t ) [ − α log ( π t ( a t ∣ s t ) ) − α H 0 ] J(\alpha) = \textcolor{red}{\mathbb{E}_{s_t\sim R,a_t\sim \pi(\cdot|s_t)}[-\alpha\log(\pi_t(a_t|s_t))-\alpha\mathcal{H}_0]} J(α)=Est∼R,at∼π(⋅∣st)[−αlog(πt(at∣st))−αH0]
1.5 Pesudocode

2. 代码实现
2.1 SAC处理连续动作空间
采用gymnasium中Pendulum-v1的连续动作环境,整体代码如下
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.distributions import Normalfrom tqdm import tqdm
import collections
import random
import numpy as np
import matplotlib.pyplot as plt
import gym# replay buffer
class ReplayBuffer():def __init__(self, capacity):self.buffer = collections.deque(maxlen=capacity)def add(self, s, r, a, s_, d):self.buffer.append((s,r,a,s_,d))def sample(self, batch_size):transitions = random.sample(self.buffer, batch_size)states, rewards, actions, next_states, dones = zip(*transitions)return np.array(states), rewards, actions, np.array(next_states), donesdef size(self):return len(self.buffer)# Actor
class PolicyNet_Continuous(nn.Module):"""动作空间符合高斯分布,输出动作空间的均值mu,和标准差std"""def __init__(self, state_dim, hidden_dim, action_dim, action_bound):super(PolicyNet_Continuous, self).__init__()self.fc1 = nn.Sequential(nn.Linear(in_features=state_dim, out_features=hidden_dim),nn.ReLU())self.fc_mu = nn.Linear(in_features=hidden_dim, out_features=action_dim)self.fc_std = nn.Sequential(nn.Linear(in_features=hidden_dim, out_features=action_dim),nn.Softplus())self.action_bound = action_bounddef forward(self, s):x = self.fc1(s)mu = self.fc_mu(x)std = self.fc_std(x)distribution = Normal(mu, std)normal_sample = distribution.rsample()normal_log_prob = distribution.log_prob(normal_sample)# get action limit to [-1,1]action = torch.tanh(normal_sample)# get tanh_normal log probabilitytanh_log_prob = normal_log_prob - torch.log(1 - torch.tanh(action).pow(2) + 1e-7)# get action boundedaction = action * self.action_boundreturn action, tanh_log_prob# Critic
class QValueNet_Continuous(nn.Module):def __init__(self, state_dim, hidden_dim, action_dim):super(QValueNet_Continuous, self).__init__()self.fc1 = nn.Sequential(nn.Linear(in_features=state_dim + action_dim, out_features=hidden_dim),nn.ReLU())self.fc2 = nn.Sequential(nn.Linear(in_features=hidden_dim, out_features=hidden_dim),nn.ReLU())self.fc_out = nn.Linear(in_features=hidden_dim, out_features=1)def forward(self, s, a):cat = torch.cat([s,a], dim=1)x = self.fc1(cat)x = self.fc2(x)return self.fc_out(x)# maximize entropy deep reinforcement learning SAC
class SAC_Continuous():def __init__(self, state_dim, hidden_dim, action_dim, action_bound,actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma,device):# actorself.actor = PolicyNet_Continuous(state_dim, hidden_dim, action_dim, action_bound).to(device)# two criticsself.critic1 = QValueNet_Continuous(state_dim, hidden_dim, action_dim).to(device)self.critic2 = QValueNet_Continuous(state_dim, hidden_dim, action_dim).to(device)# two target criticsself.target_critic1 = QValueNet_Continuous(state_dim, hidden_dim, action_dim).to(device)self.target_critic2 = QValueNet_Continuous(state_dim, hidden_dim, action_dim).to(device)# initialize with same parametersself.target_critic1.load_state_dict(self.critic1.state_dict())self.target_critic2.load_state_dict(self.critic2.state_dict())# specify optimizersself.optimizer_actor = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)self.optimizer_critic1 = torch.optim.Adam(self.critic1.parameters(), lr=critic_lr)self.optimizer_critic2 = torch.optim.Adam(self.critic2.parameters(), lr=critic_lr)# 使用alpha的log值可以使训练稳定self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float, requires_grad = True)self.optimizer_log_alpha = torch.optim.Adam([self.log_alpha], lr=alpha_lr)self.target_entropy = target_entropyself.gamma = gammaself.tau = tauself.device = devicedef take_action(self, state):state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)action, _ = self.actor(state)return [action.item()]# calculate td targetdef calc_target(self, rewards, next_states, dones):next_action, log_prob = self.actor(next_states)entropy = -log_probq1_values = self.target_critic1(next_states, next_action)q2_values = self.target_critic2(next_states, next_action)next_values = torch.min(q1_values, q2_values) + self.log_alpha.exp() * entropytd_target = rewards + self.gamma * next_values * (1-dones)return td_target# soft update methoddef soft_update(self, net, target_net):for param_target, param in zip(target_net.parameters(), net.parameters()):param_target.data.copy_(param_target.data * (1.0-self.tau) + param.data * self.tau)def update(self, transition_dict):states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1,1).to(self.device)next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)rewards = (rewards + 8.0) / 8.0 #对倒立摆环境的奖励进行重塑,方便训练# update two Q-value networktd_target = self.calc_target(rewards, next_states, dones).detach()critic1_loss = torch.mean(F.mse_loss(td_target, self.critic1(states, actions)))critic2_loss = torch.mean(F.mse_loss(td_target, self.critic2(states, actions)))self.optimizer_critic1.zero_grad()critic1_loss.backward()self.optimizer_critic1.step()self.optimizer_critic2.zero_grad()critic2_loss.backward()self.optimizer_critic2.step()# update policy networknew_actions, log_prob = self.actor(states)entropy = - log_probq1_value = self.critic1(states, new_actions)q2_value = self.critic2(states, new_actions)actor_loss = torch.mean(-self.log_alpha.exp() * entropy - torch.min(q1_value, q2_value))self.optimizer_actor.zero_grad()actor_loss.backward()self.optimizer_actor.step()# update temperature alphaalpha_loss = torch.mean((entropy - self.target_entropy).detach() * self.log_alpha.exp())self.optimizer_log_alpha.zero_grad()alpha_loss.backward()self.optimizer_log_alpha.step()# soft update target Q-value networkself.soft_update(self.critic1, self.target_critic1)self.soft_update(self.critic2, self.target_critic2)def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size, render, seed_number):return_list = []for i in range(10):with tqdm(total=int(num_episodes/10), desc='Iteration %d'%(i+1)) as pbar:for i_episode in range(int(num_episodes/10)):observation, _ = env.reset(seed=seed_number)done = Falseepisode_return = 0while not done:if render:env.render()action = agent.take_action(observation)observation_, reward, terminated, truncated, _ = env.step(action)done = terminated or truncatedreplay_buffer.add(observation, action, reward, observation_, done)# swap statesobservation = observation_episode_return += rewardif replay_buffer.size() > minimal_size:b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)transition_dict = {'states': b_s,'actions': b_a,'rewards': b_r,'next_states': b_ns,'dones': b_d}agent.update(transition_dict)return_list.append(episode_return)if(i_episode+1) % 10 == 0:pbar.set_postfix({'episode': '%d'%(num_episodes/10 * i + i_episode + 1),'return': "%.3f"%(np.mean(return_list[-10:]))})pbar.update(1)env.close()return return_listdef moving_average(a, window_size):cumulative_sum = np.cumsum(np.insert(a, 0, 0)) middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_sizer = np.arange(1, window_size-1, 2)begin = np.cumsum(a[:window_size-1])[::2] / rend = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]return np.concatenate((begin, middle, end))def plot_curve(return_list, mv_return, algorithm_name, env_name):episodes_list = list(range(len(return_list)))plt.plot(episodes_list, return_list, c='gray', alpha=0.6)plt.plot(episodes_list, mv_return)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('{} on {}'.format(algorithm_name, env_name))plt.show()if __name__ == "__main__":# reproducibleseed_number = 0random.seed(seed_number)np.random.seed(seed_number)torch.manual_seed(seed_number)num_episodes = 150 # episodes lengthhidden_dim = 128 # hidden layers dimensiongamma = 0.98 # discounted rateactor_lr = 1e-4 # lr of actorcritic_lr = 1e-3 # lr of criticalpha_lr = 1e-4tau = 0.005 # soft update parameterbuffer_size = 10000minimal_size = 1000batch_size = 64device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')env_name = 'Pendulum-v1'render = Falseif render:env = gym.make(id=env_name, render_mode='human')else:env = gym.make(id=env_name)state_dim = env.observation_space.shape[0]action_dim = env.action_space.shape[0] action_bound = env.action_space.high[0]# entropy初始化为动作空间维度的负数target_entropy = - env.action_space.shape[0]replaybuffer = ReplayBuffer(buffer_size)agent = SAC_Continuous(state_dim, hidden_dim, action_dim, action_bound, actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma, device)return_list = train_off_policy_agent(env, agent, num_episodes, replaybuffer, minimal_size, batch_size, render, seed_number)mv_return = moving_average(return_list, 9)plot_curve(return_list, mv_return, 'SAC', env_name)
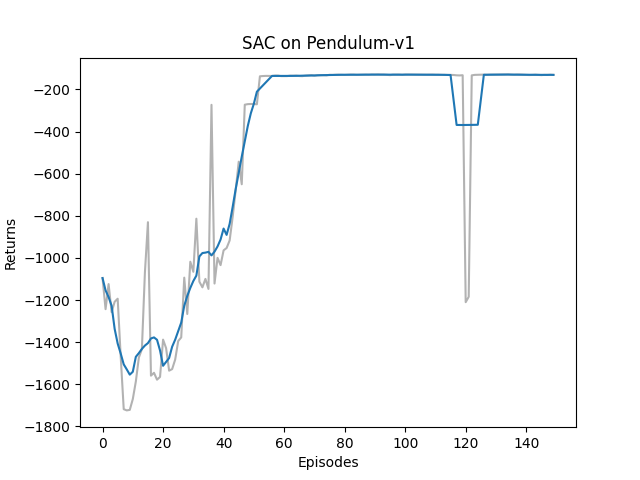
所获得的回报曲线如下图
2.2 SAC处理离散动作空间
采用gaymnasium中的CartPole-v1离散动作空间的环境。
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.distributions import Categoricalfrom tqdm import tqdm
import collections
import random
import numpy as np
import matplotlib.pyplot as plt
import gym# replay buffer
class ReplayBuffer():def __init__(self, capacity):self.buffer = collections.deque(maxlen=capacity)def add(self, s, r, a, s_, d):self.buffer.append((s,r,a,s_,d))def sample(self, batch_size):transitions = random.sample(self.buffer, batch_size)states, rewards, actions, next_states, dones = zip(*transitions)return np.array(states), rewards, actions, np.array(next_states), donesdef size(self):return len(self.buffer)# Actor
class PolicyNet_Discrete(nn.Module):"""动作空间服从离散的概率分布,输出每个动作的概率值"""def __init__(self, state_dim, hidden_dim, action_dim):super(PolicyNet_Discrete, self).__init__()self.fc1 = nn.Sequential(nn.Linear(in_features=state_dim, out_features=hidden_dim),nn.ReLU())self.fc2 = nn.Sequential(nn.Linear(in_features=hidden_dim, out_features=action_dim),nn.Softmax(dim=1))def forward(self, s):x = self.fc1(s)return self.fc2(x)# Critic
class QValueNet_Discrete(nn.Module):def __init__(self, state_dim, hidden_dim, action_dim):super(QValueNet_Discrete, self).__init__()self.fc1 = nn.Sequential(nn.Linear(in_features=state_dim, out_features=hidden_dim),nn.ReLU())self.fc2 = nn.Linear(in_features=hidden_dim, out_features=action_dim)def forward(self, s):x = self.fc1(s)return self.fc2(x)# maximize entropy deep reinforcement learning SAC
class SAC_Continuous():def __init__(self, state_dim, hidden_dim, action_dim,actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma,device):# actorself.actor = PolicyNet_Discrete(state_dim, hidden_dim, action_dim).to(device)# two criticsself.critic1 = QValueNet_Discrete(state_dim, hidden_dim, action_dim).to(device)self.critic2 = QValueNet_Discrete(state_dim, hidden_dim, action_dim).to(device)# two target criticsself.target_critic1 = QValueNet_Discrete(state_dim, hidden_dim, action_dim).to(device)self.target_critic2 = QValueNet_Discrete(state_dim, hidden_dim, action_dim).to(device)# initialize with same parametersself.target_critic1.load_state_dict(self.critic1.state_dict())self.target_critic2.load_state_dict(self.critic2.state_dict())# specify optimizersself.optimizer_actor = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)self.optimizer_critic1 = torch.optim.Adam(self.critic1.parameters(), lr=critic_lr)self.optimizer_critic2 = torch.optim.Adam(self.critic2.parameters(), lr=critic_lr)# 使用alpha的log值可以使训练稳定self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float, requires_grad = True)self.optimizer_log_alpha = torch.optim.Adam([self.log_alpha], lr=alpha_lr)self.target_entropy = target_entropyself.gamma = gammaself.tau = tauself.device = devicedef take_action(self, state):state = torch.tensor(np.array([state]), dtype=torch.float).to(self.device)probs = self.actor(state)action_dist = Categorical(probs)action = action_dist.sample()return action.item()# calculate td targetdef calc_target(self, rewards, next_states, dones):next_probs = self.actor(next_states)next_log_probs = torch.log(next_probs + 1e-8)entropy = -torch.sum(next_probs * next_log_probs, dim=1, keepdim=True)q1_values = self.target_critic1(next_states)q2_values = self.target_critic2(next_states)min_qvalue = torch.sum(next_probs * torch.min(q1_values, q2_values),dim=1,keepdim=True)next_value = min_qvalue + self.log_alpha.exp() * entropytd_target = rewards + self.gamma * next_value * (1 - dones)return td_target# soft update methoddef soft_update(self, net, target_net):for param_target, param in zip(target_net.parameters(), net.parameters()):param_target.data.copy_(param_target.data * (1.0-self.tau) + param.data * self.tau)def update(self, transition_dict):states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device)actions = torch.tensor(transition_dict['actions'], dtype=torch.int64).view(-1,1).to(self.device)next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device)rewards = (rewards + 8.0) / 8.0 #对倒立摆环境的奖励进行重塑,方便训练# update two Q-value networktd_target = self.calc_target(rewards, next_states, dones).detach()critic1_loss = torch.mean(F.mse_loss(td_target, self.critic1(states).gather(dim=1,index=actions)))critic2_loss = torch.mean(F.mse_loss(td_target, self.critic2(states).gather(dim=1,index=actions)))self.optimizer_critic1.zero_grad()critic1_loss.backward()self.optimizer_critic1.step()self.optimizer_critic2.zero_grad()critic2_loss.backward()self.optimizer_critic2.step()# update policy networkprobs = self.actor(states)log_probs = torch.log(probs + 1e-8)entropy = -torch.sum(probs * log_probs, dim=1, keepdim=True)q1_value = self.critic1(states)q2_value = self.critic2(states)min_qvalue = torch.sum(probs * torch.min(q1_value, q2_value),dim=1,keepdim=True) # 直接根据概率计算期望actor_loss = torch.mean(-self.log_alpha.exp() * entropy - min_qvalue)self.optimizer_actor.zero_grad()actor_loss.backward()self.optimizer_actor.step()# update temperature alphaalpha_loss = torch.mean((entropy - self.target_entropy).detach() * self.log_alpha.exp())self.optimizer_log_alpha.zero_grad()alpha_loss.backward()self.optimizer_log_alpha.step()# soft update target Q-value networkself.soft_update(self.critic1, self.target_critic1)self.soft_update(self.critic2, self.target_critic2)def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size, render, seed_number):return_list = []for i in range(10):with tqdm(total=int(num_episodes/10), desc='Iteration %d'%(i+1)) as pbar:for i_episode in range(int(num_episodes/10)):observation, _ = env.reset(seed=seed_number)done = Falseepisode_return = 0while not done:if render:env.render()action = agent.take_action(observation)observation_, reward, terminated, truncated, _ = env.step(action)done = terminated or truncatedreplay_buffer.add(observation, action, reward, observation_, done)# swap statesobservation = observation_episode_return += rewardif replay_buffer.size() > minimal_size:b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)transition_dict = {'states': b_s,'actions': b_a,'rewards': b_r,'next_states': b_ns,'dones': b_d}agent.update(transition_dict)return_list.append(episode_return)if(i_episode+1) % 10 == 0:pbar.set_postfix({'episode': '%d'%(num_episodes/10 * i + i_episode + 1),'return': "%.3f"%(np.mean(return_list[-10:]))})pbar.update(1)env.close()return return_listdef moving_average(a, window_size):cumulative_sum = np.cumsum(np.insert(a, 0, 0)) middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_sizer = np.arange(1, window_size-1, 2)begin = np.cumsum(a[:window_size-1])[::2] / rend = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]return np.concatenate((begin, middle, end))def plot_curve(return_list, mv_return, algorithm_name, env_name):episodes_list = list(range(len(return_list)))plt.plot(episodes_list, return_list, c='gray', alpha=0.6)plt.plot(episodes_list, mv_return)plt.xlabel('Episodes')plt.ylabel('Returns')plt.title('{} on {}'.format(algorithm_name, env_name))plt.show()if __name__ == "__main__":# reproducibleseed_number = 0random.seed(seed_number)np.random.seed(seed_number)torch.manual_seed(seed_number)num_episodes = 200 # episodes lengthhidden_dim = 128 # hidden layers dimensiongamma = 0.98 # discounted rateactor_lr = 1e-3 # lr of actorcritic_lr = 1e-2 # lr of criticalpha_lr = 1e-2tau = 0.005 # soft update parameterbuffer_size = 10000minimal_size = 500batch_size = 64device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')env_name = 'CartPole-v1'render = Falseif render:env = gym.make(id=env_name, render_mode='human')else:env = gym.make(id=env_name)state_dim = env.observation_space.shape[0]action_dim = env.action_space.n # entropy初始化为-1target_entropy = -1replaybuffer = ReplayBuffer(buffer_size)agent = SAC_Continuous(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma, device)return_list = train_off_policy_agent(env, agent, num_episodes, replaybuffer, minimal_size, batch_size, render, seed_number)mv_return = moving_average(return_list, 9)plot_curve(return_list, mv_return, 'SAC', env_name)Reference
Hands on RL
SAC(Soft Actor-Critic)阅读笔记
Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
相关文章:

Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC)
Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC) 文章目录 Hands on RL 之 Off-policy Maximum Entropy Actor-Critic (SAC)1. 理论基础1.1 Maximum Entropy Reinforcement Learning, MERL1.2 Soft Policy Evaluation and Soft Policy Improvement in SAC1.3 Tw…...

JavaScript中的this指向,call、apply、bind的简单实现
JavaScript中的this this是JavaScript中一个特殊关键字,用于指代当前执行上下文中的对象。它的难以理解之处就是值不是固定的,是再函数被调用时根据调用场景动态确定的,主要根据函数的调用方式来决定this指向的对象。this 的值在函数被调用时…...
Linux学习之基本指令一
在学习Linux下的基本指令之前首先大家要知道Linux下一切皆目录,我们的操作基本上也都是对目录的操作,这里我们可以联想我们是如何在windows上是如何操作的,只是形式上不同,类比学习更容易理解。 目录 01.ls指令 02. pwd命令 0…...

appium默认60秒关闭应用的问题
问题:appium默认启动一个应用的session过期时间是60秒到时间会自动停了刚启动的应用,工作台打印:info: [debug] We shut down because no new commands came in的日志 分析:--command-timeout 60 The default command timeout fo…...
Docker 容器内无法使用vim命令 解决方法
目录 1. 问题所示2. 原理分析3. 解决方法1. 问题所示 进入Docker容器后 无法使用vim编辑器,出现如下问题:bash: vim: command not found 如图所示: 想着通过apt-get 安装vim,出现如下问题: root@b9f0fd330d5b:/# apt-get install vim Reading package lists... Done B…...
Django的简介安装与配置及两大设计模式
一.Djang的介绍 1.Django是什么 Django 是使用 Python 语言开发的一款免费而且开源的 Web 应用框架。 由于 Python 语言的跨平台性,所以 Django 同样支持 Windows、Linux 和 Mac 系统。 在 Python 语言炽手可热的当下,Django 也迅速的崛起,在…...

Mybatis分页插件——PageHelper
一、定义 PageHelper用在mybatis插件里面,可以自动的为最近的sql语句进行分页查询,提供分页的页码size和每页数量num,在查询过程中hi自动的拼接limit关键字,不用再改写sql语句了 在PageHelper.startPage(); 在启动查询…...

k8s认证详解 k8s证书详解 2023推荐
推荐阅读 https://www.yii666.com/blog/478731.html?actiononAll 在 Kube-apiserver 中提供了很多认证方式,其中最常用的就是 TLS 认证,当然也有 BootstrapToken,BasicAuth 认证等,只要有一个认证通过,那么 Kube-api…...

php初解
php是什么? PHP,全称 Hypertext Preprocessor ,中文翻译“超文本预处理器”。 PHP是一种被广泛应用的开源通用脚本语言,尤其适用于 Web 开发。 拥有快速,灵活,实用的特点,PHP能做任何事…...
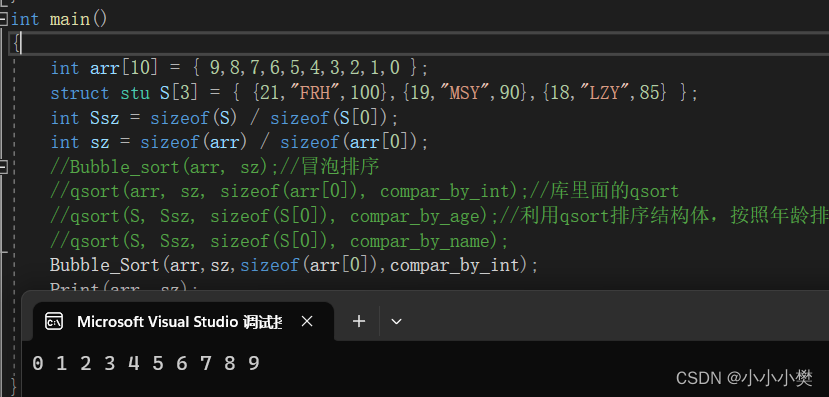
【C语言】回调函数,qsort排序函数的使用和自己实现,超详解
文章目录 前言一、回调函数是什么二、回调函数的使用1.使用标准库中的qsort函数2.利用qsort函数对结构体数组进行排序 三、实现qsort函数总结 先记录一下访问量突破2000啦,谢谢大家支持!!! 这里是上期指针进阶链接,方便…...
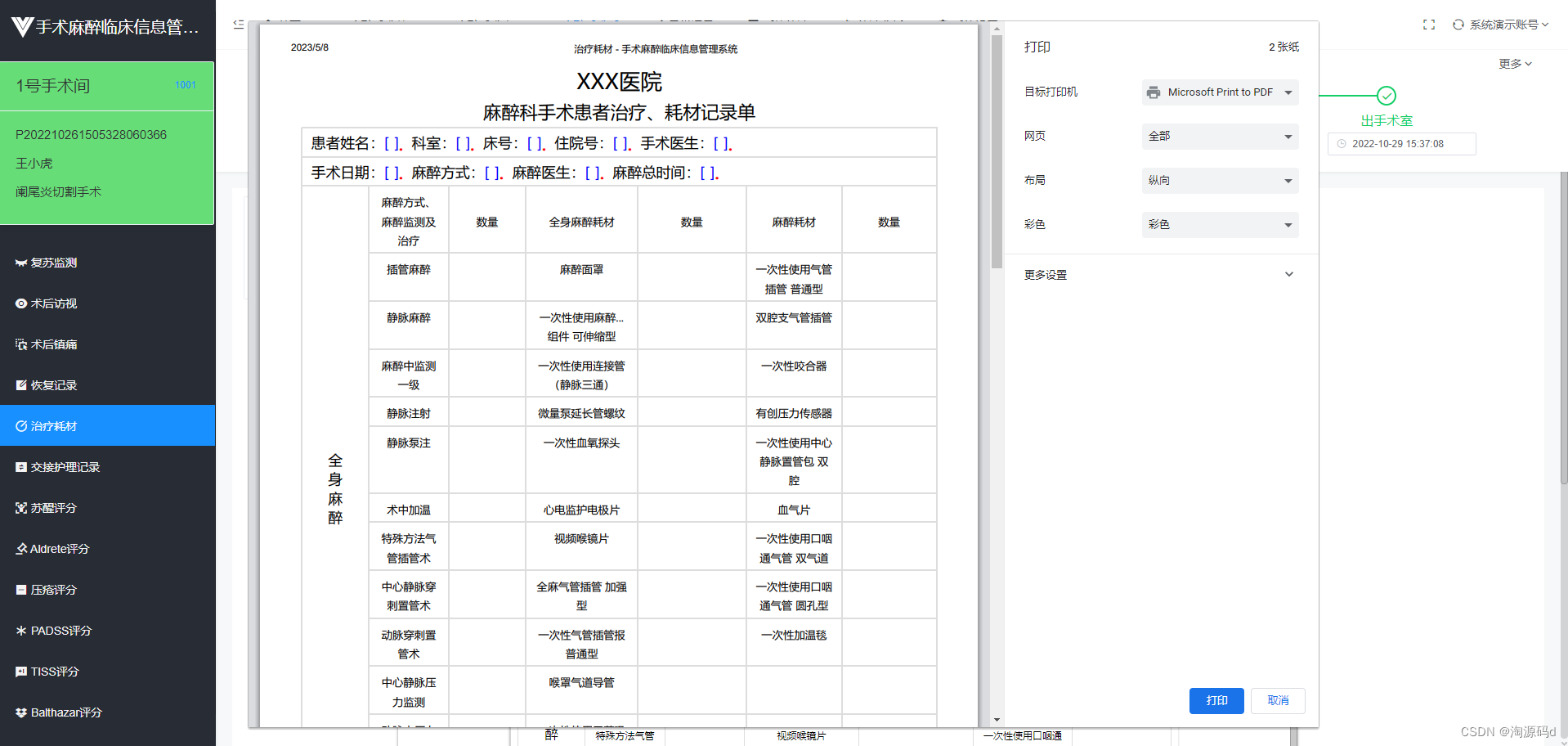
PHP手术麻醉系统源码,自动生成麻醉和护理医疗文书
一套手术麻醉系统源码,可二次开发 手术室麻醉临床信息系统(AIMS)是应用于医院手术室、麻醉科室的计算机软件系统。该系统针对整个围术期,对病人进行全程跟踪与信息管理,自动集成病人HIS、LIS、RIS、PACS信息࿰…...
内网穿透实战应用——【通过cpolar分享本地电脑上有趣的照片:发布piwigo网页】
通过cpolar分享本地电脑上有趣的照片:发布piwigo网页 文章目录 通过cpolar分享本地电脑上有趣的照片:发布piwigo网页前言1. 设定一条内网穿透数据隧道2. 与piwigo网站绑定3. 在创建隧道界面填写关键信息4. 隧道创建完成 总结 前言 首先在本地电脑上部署…...
iPhone删除的照片能恢复吗?不小心误删了照片怎么找回?
iPhone最近删除清空了照片还能恢复吗?大家都知道,照片对于我们来说是承载着美好回忆的一种形式。它记录着我们的平淡生活,也留住了我们的美好瞬间,具有极其重要的纪念价值。 照片不小心误删是一件非常难受的事,那么iP…...
LeetCode--HOT100题(32)
目录 题目描述:138. 复制带随机指针的链表(中等)题目接口解题思路代码 PS: 题目描述:138. 复制带随机指针的链表(中等) 给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random &…...
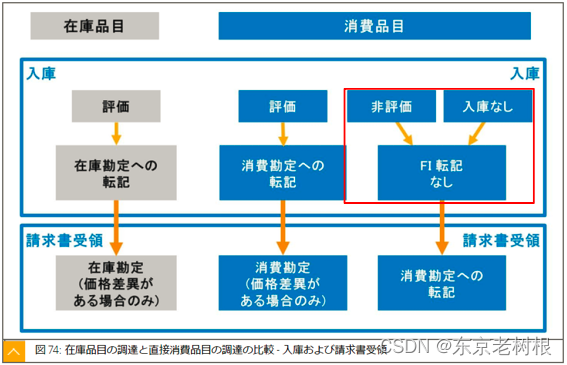
SAP MM学习笔记24-以评估收货(评价)和非评估收货(非评价)
SAP 中 有评价入库(评估收货)和非评价入库(非评估收货)两种入库方式。 一般来说在库品目会采用评价入库,而消费品目,会采用非评价入库。 其实评价入库,非评价入库对外都无所谓的,人…...
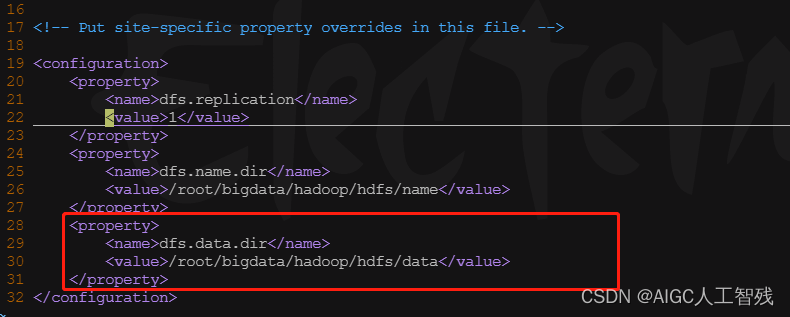
Hadoop的DataNode无法启动的解决方案
Hadoop重启一次,里面的数据需要重新导入,发现无法导入数据,查看jps发现是DataNode没有启动,重新启动发现也无法启动,原因是前面重新启动NameNode,里面的文件格式化一次,DataNode的文件不一致&am…...

re中的match和search有什么区别?
问题:请说明以下re模块中的match和search有什么区别? re.match()与re.search()的区别 re.match()只匹配字符串的开始,如果字符串开始不符合正则表达式,则匹配失败,结果返回None,而re.search()匹配整个字符串,直到找到一个匹配 re.search() re.search()扫描整个字符串并…...
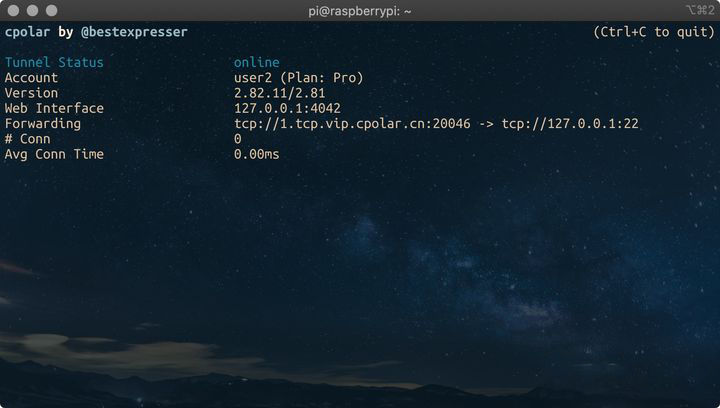
《内网穿透》无需公网IP,公网SSH远程访问家中的树莓派
文章目录 前言 如何通过 SSH 连接到树莓派步骤1. 在 Raspberry Pi 上启用 SSH步骤2. 查找树莓派的 IP 地址步骤3. SSH 到你的树莓派步骤 4. 在任何地点访问家中的树莓派4.1 安装 Cpolar内网穿透4.2 cpolar进行token认证4.3 配置cpolar服务开机自启动4.4 查看映射到公网的隧道地…...
.net连接mysql,提示找不到请求的 .Net Framework Data Provider。可能没有安装
开发完成的.net程序需要连接mysql数据库,在个人电脑上运行没问题,别人运行时提示“提示找不到请求的 .Net Framework Data Provider。可能没有安装”。经过查询,安装Connector/NET 8.1.0,下载地址如下所示: https://d…...
销售自动化管理软件是什么,销售自动化管理软件有什么优势
阅读本文您可以了解:1、销售自动化管理软件是什么;2、销售自动化管理软件的优势 一、销售自动化管理软件是什么 销售自动化管理软件是一种用于帮助企业有效管理销售流程和客户关系的工具。它集成了各种功能和工具,以简化和自动化销售团队的任…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
