【数据结构】二叉树篇| 纲领思路01+刷题

- 博主简介:努力学习的22级计算机科学与技术本科生一枚🌸
- 博主主页: @是瑶瑶子啦
- 每日一言🌼: 所谓自由,不是随心所欲,而是自我主宰。——康德
目录
- 一、二叉树刷题纲领
- 二、刷题
- 1、104. 二叉树的最大深度
- 2、 二叉树的前序遍历(非递归)
- 3、 二叉树的直径
一、二叉树刷题纲领
-
🍊 二叉树解题的思维模式分两类:
- 1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。(对应:回溯算法)
void traverse(TreeNode root) {if (root == null) {return;}// 前序位置traverse(root.left);// 中序位置traverse(root.right);// 后序位置 }- 2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。(对应:动态规划算法)
-
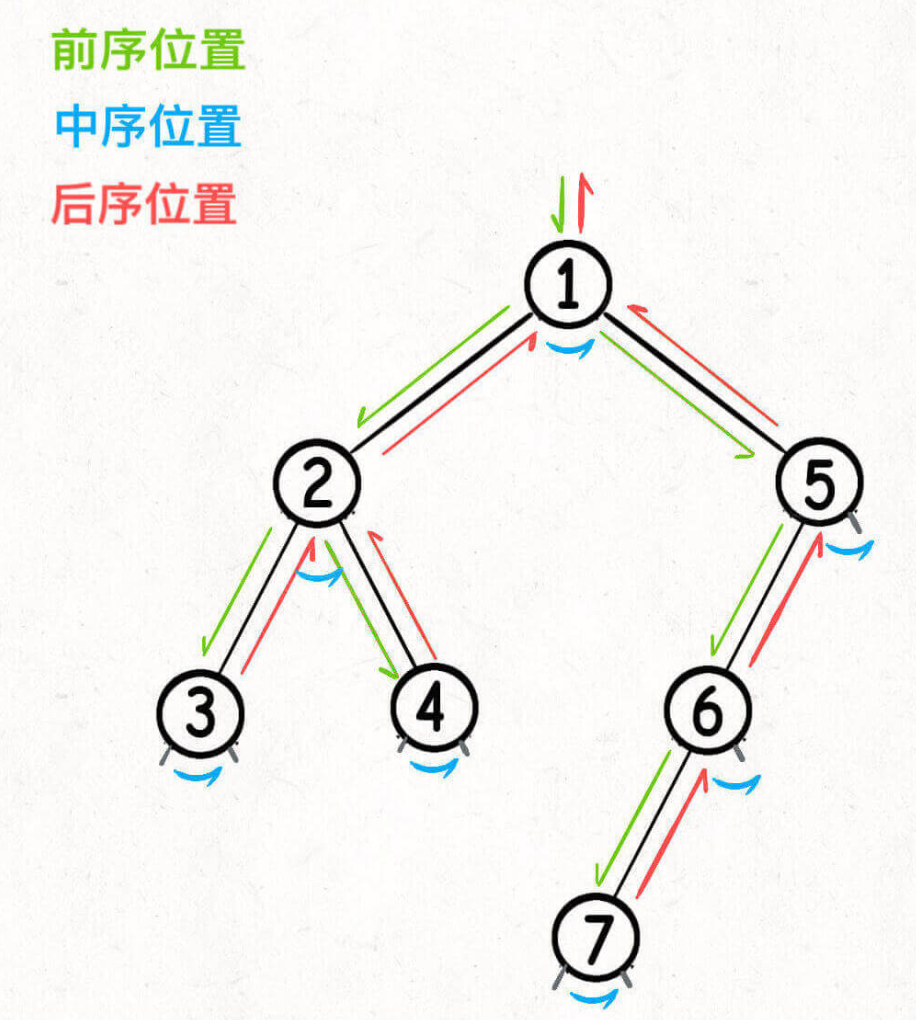
🍊 前中后序
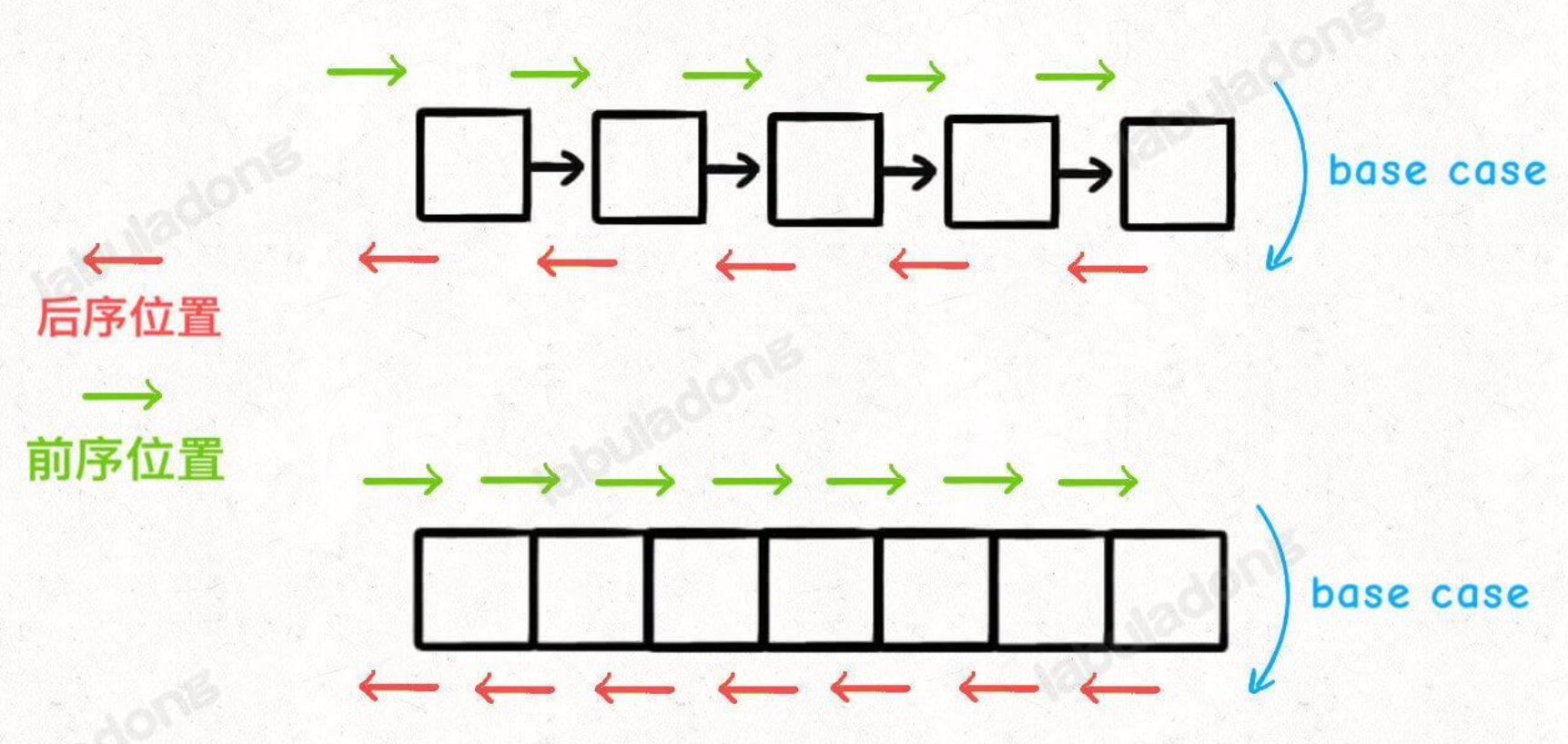
- 所谓前序位置,就是刚进入一个节点(元素)的时候,后序位置就是即将离开一个节点(元素)的时候,那么进一步,你把代码写在不同位置,代码执行的时机也不同
- 前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据。
- 🌟二叉树的所有问题,就是让你在前中后序位置注入巧妙的代码逻辑,去达到自己的目的,你只需要单独思考每一个节点应该做什么,其他的不用你管,抛给二叉树遍历框架,递归会在所有节点上做相同的操作。
-
🍊一道二叉树的题目时的通用思考过程
-
是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现。
-
是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值。
-
无论使用哪一种思维模式,你都要明白二叉树的每一个节点需要做什么,需要在什么时候(前中后序)做。
-
二、刷题
1、104. 二叉树的最大深度
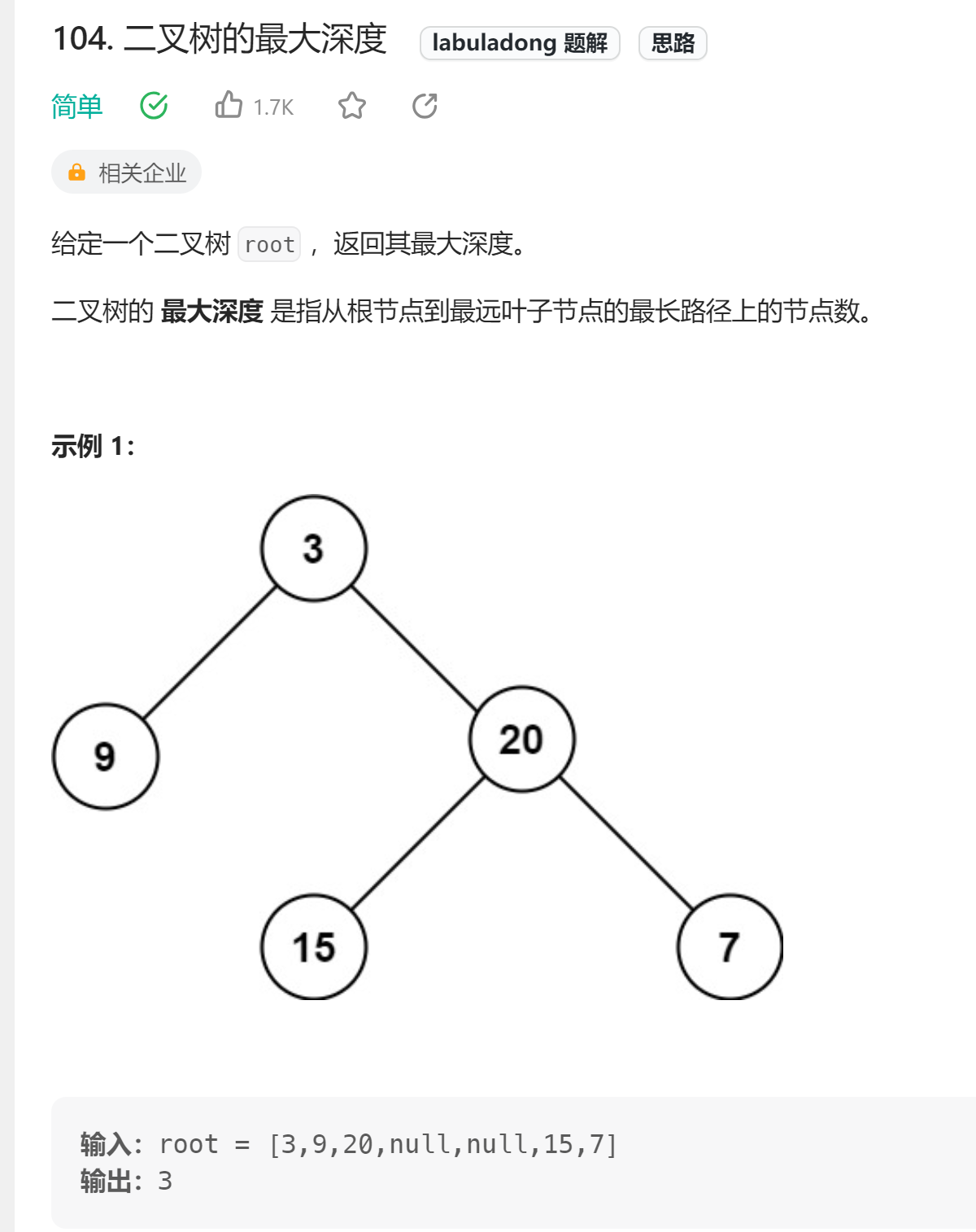
🔗104. 二叉树的最大深度
-
👧🏻思路:分解成子问题,maxDepth = 1 + 左子树最大高度+右子树最大高度
-
🙇🏻♀️代码:
public int maxDepth(TreeNode root) {//临界条件if(root == null){return 0;}int leftHeight = maxDepth(root.left);//求左子树最大高度int rightHeight = maxDepth(root.right);//求右子树最大高度return 1 + Math.max(leftHeight, rightHeight);}
2、 二叉树的前序遍历(非递归)
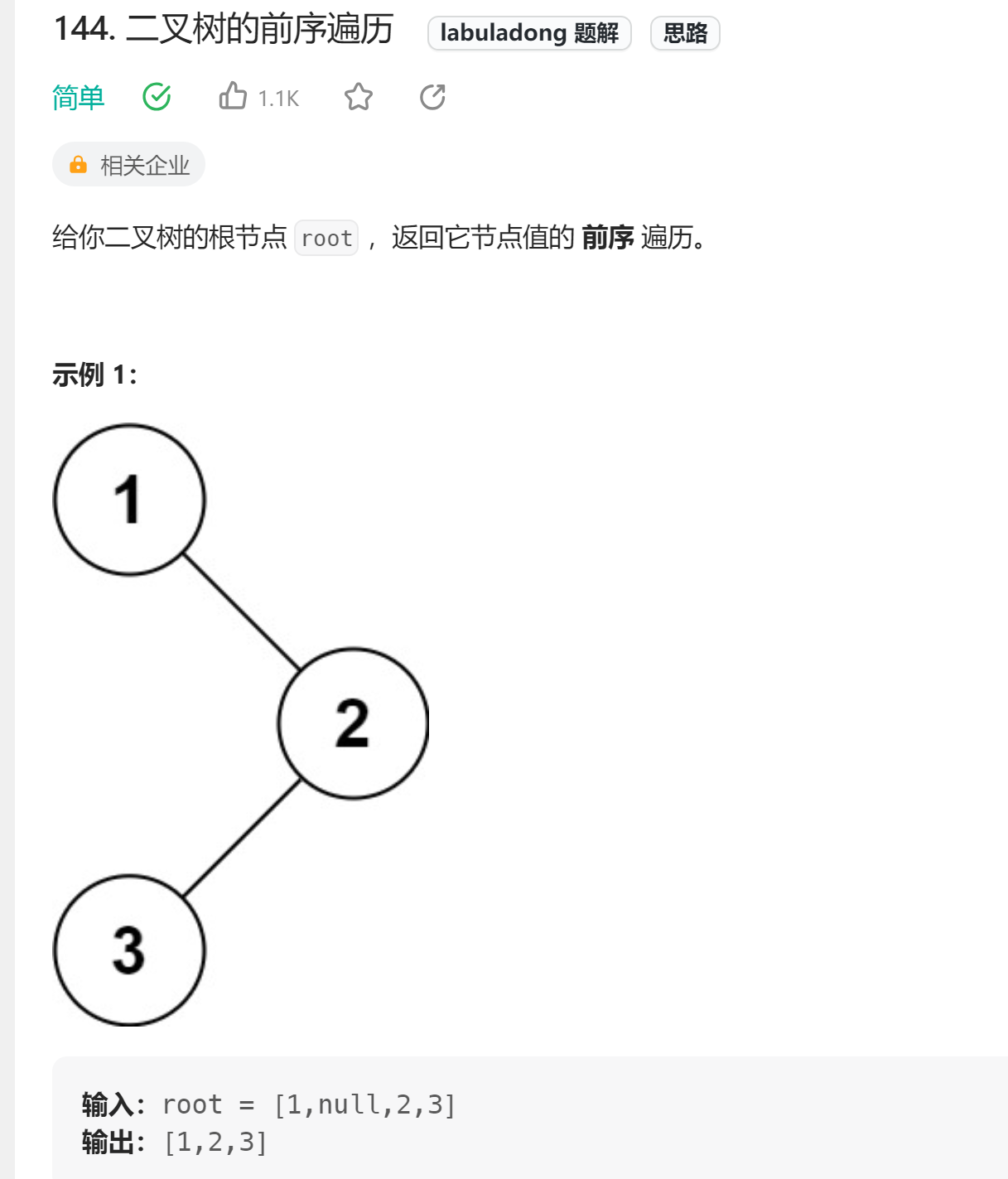
🔗144. 二叉树的前序遍历
-
👧🏻思路:分解成子问题,递归序列 = add(自身节点)+ add(左子树的递归序列) + add(右子树的递归序列)
-
🙇🏻♀️代码:
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ret = new LinkedList<>();if(root == null){return ret;}ret.add(root.val);if(root.left!=null){List<Integer> leftList = preorderTraversal(root.left);ret.addAll(leftList);}if(root.right!=null){List<Integer> rightList = preorderTraversal(root.right);ret.addAll(rightList);}return ret;}
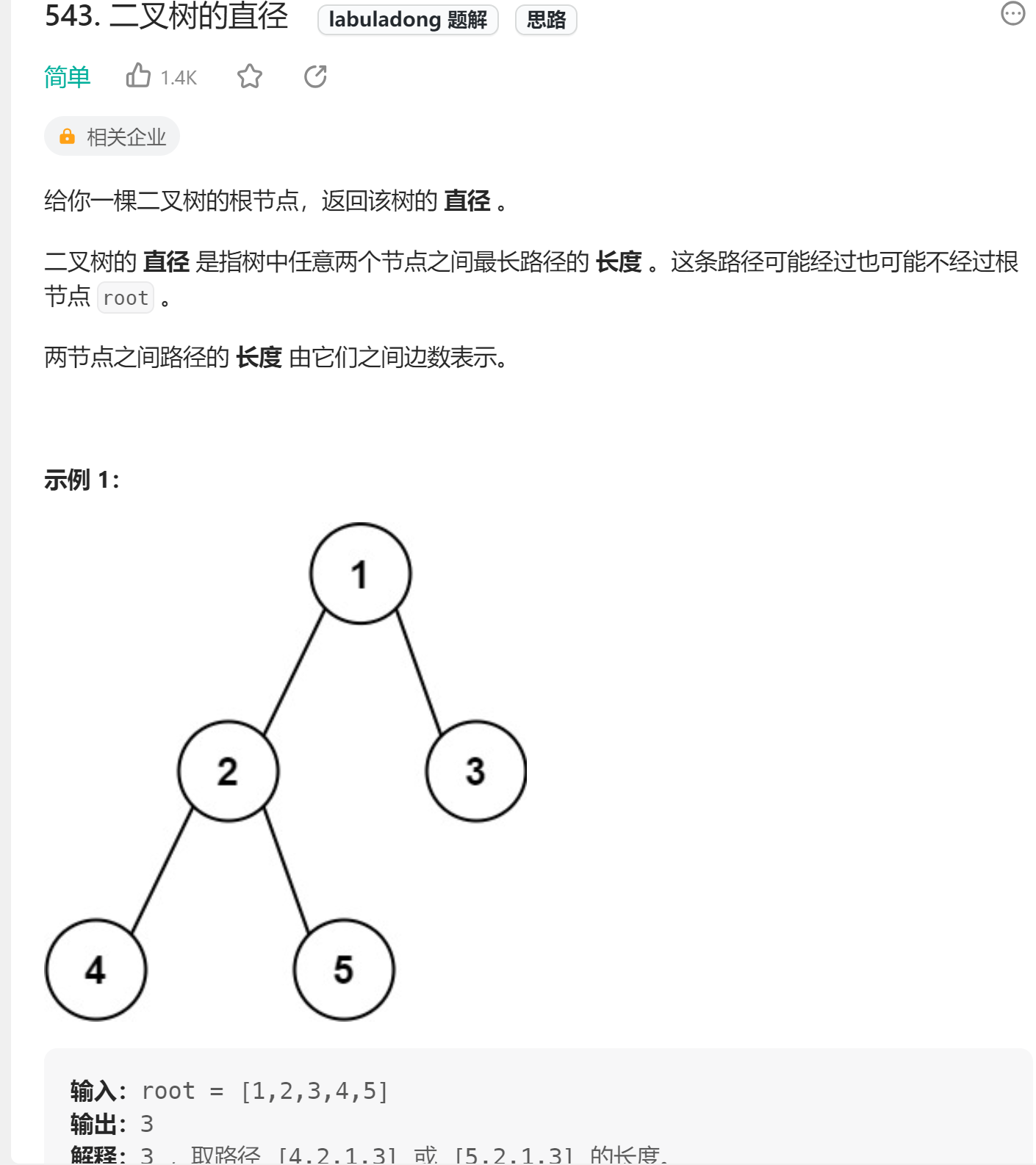
3、 二叉树的直径
🔗543. 二叉树的直径
-
👧🏻思路:两种模式的结合,首先大的背景是利用
maxDepth进行二叉树的后序遍历+求当前节点左右子树的最大高度.注意需要一个外部变量maxDiameter来时刻更新最大直径。(这种思路是O(n)的时间复杂度,可以用遍历每个节点+求当前节点的最大直径,思路是一样的,但是复杂度度是O(n2),因为在本方法中在求maxDepth的时候就已经顺带遍历了整个节点!)

-
🙇🏻♀️代码:
public int maxDiameter;public int diameterOfBinaryTree(TreeNode root) {maxDepth(root);return maxDiameter;}public int maxDepth(TreeNode root) {if(root == null){return 0;}//计算当前节点的左子树最大高度int leftH = maxDepth(root.left);//计算当前节点的右子树的最大高度int rightH = maxDepth(root.right);maxDiameter = Math.max(maxDiameter,leftH + rightH);//更新maxDiameterreturn 1 + Math.max(leftH, rightH);}
💐若有不懂的地方,欢迎随时在评论区or私信找瑶瑶子交流讨论🌺

-
Java岛冒险记【从小白到大佬之路】
-
LeetCode每日一题–进击大厂
-
Go语言核心编程
-
算法
相关文章:

【数据结构】二叉树篇| 纲领思路01+刷题
博主简介:努力学习的22级计算机科学与技术本科生一枚🌸博主主页: 是瑶瑶子啦每日一言🌼: 所谓自由,不是随心所欲,而是自我主宰。——康德 目录 一、二叉树刷题纲领二、刷题1、104. 二叉树的最大深度2、 二叉…...

系统架构设计师---计算机基础知识之数据库系统结构与规范化
目录 一、基本概念 二、 数据库的结构 三、常用的数据模型 概念数据模型...
PyCharm连接Docker中的容器(ubuntu)
一、为什么要用Pycharm链接Docker中的ubuntu 因为在进行深度学习的时候,基于windows系统在开发的过程中,老是出现很多问题,大多数是环境问题。 尽管安装了Conda,也不能很好的解决问题,使用ubuntu是最好的选择。 二、…...
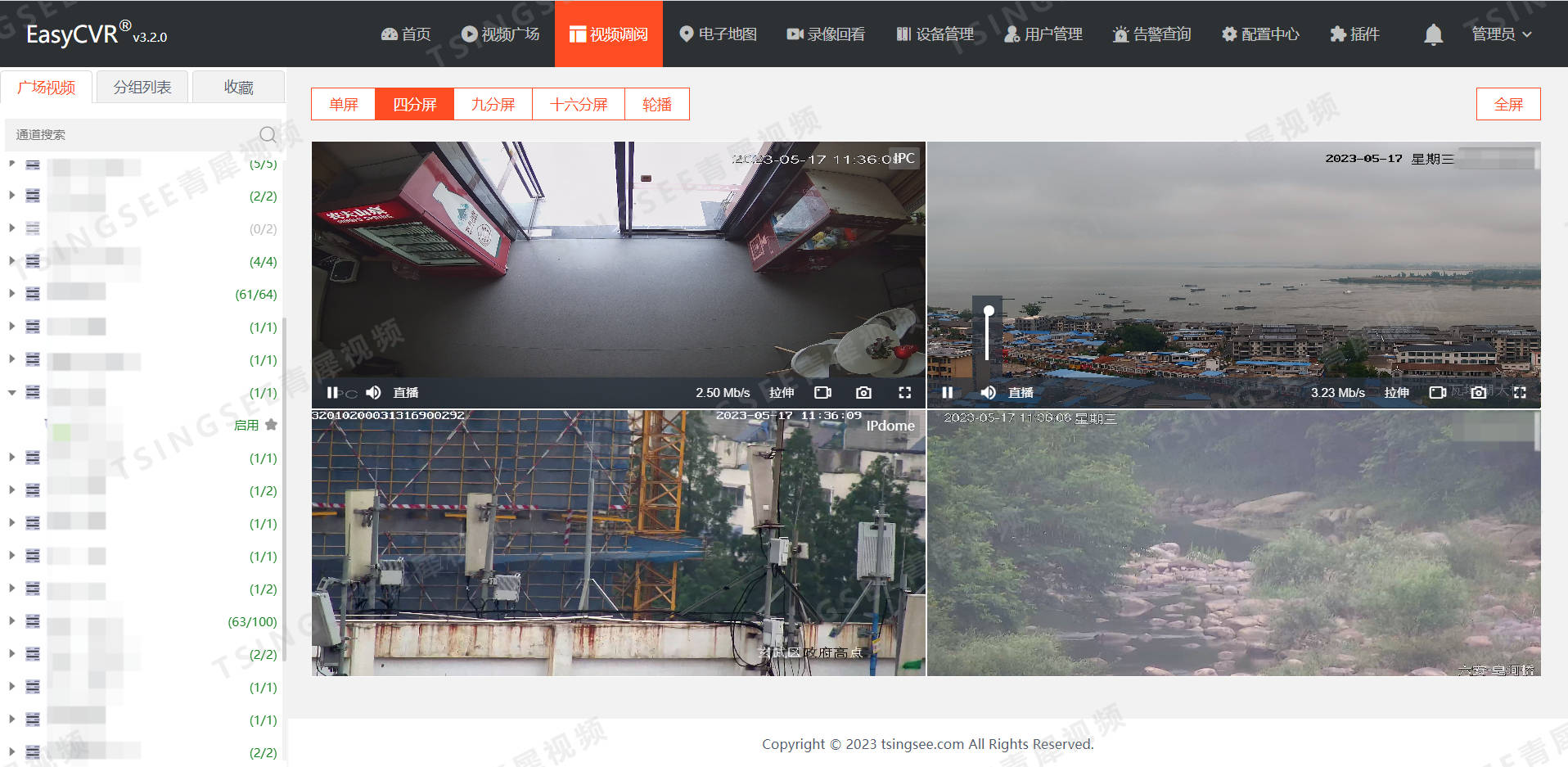
安防视频汇聚平台EasyCVR视频监控综合管理平台H.265转码功能更新,新增分辨率配置的具体步骤
安防视频集中存储EasyCVR视频监控综合管理平台可以根据不同的场景需求,让平台在内网、专网、VPN、广域网、互联网等各种环境下进行音视频的采集、接入与多端分发。在视频能力上,视频云存储平台EasyCVR可实现视频实时直播、云端录像、视频云存储、视频存储…...
全平台数据(数据库)管理工具 DataCap 管理 Rainbond 上的所有数据库
DataCap是用于数据转换、集成和可视化的集成软件,支持多种数据源、文件类型、大数据相关数据库、关系数据库、NoSQL数据库等。通过该 DataCap 可以实现对多个数据源的管理,对数据源下的数据进行各种操作转换,制作数据图表,监控数据…...

“深入探究JVM内部机制:从字节码到实际执行“
标题:深入探究JVM内部机制:从字节码到实际执行 摘要:本文将深入探究Java虚拟机(JVM)的内部机制,从字节码的生成、类加载、字节码解释和即时编译等环节,详细介绍JVM是如何将Java程序的字节码转化…...
C++写文件,直接写入结构体
C写文件,直接写入结构体 以前写文件都是写入字符串或者二进制再或者就是一些配置文件,今天介绍一下直接写入结构体,可以在软件参数较多的时候直接进行读写,直接将整个结构体写入和读取,看代码: #include&…...
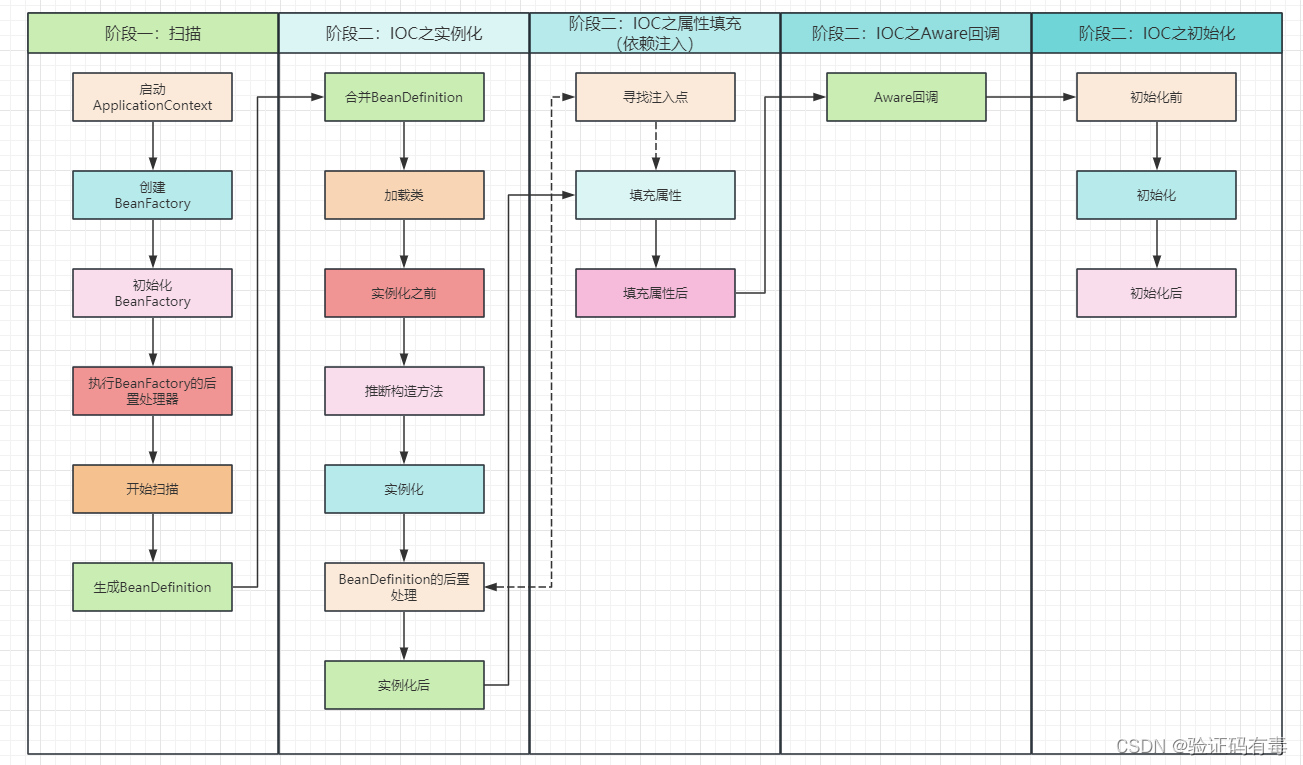
【Spring专题】Spring之Bean的生命周期源码解析——阶段二(二)(IOC之属性填充/依赖注入)
目录 前言阅读准备阅读指引阅读建议 课程内容一、依赖注入方式(前置知识)1.1 手动注入1.2 自动注入1.2.1 XML的autowire自动注入1.2.1.1 byType:按照类型进行注入1.2.1.2 byName:按照名称进行注入1.2.1.3 constructor:…...

线程|线程的使用、四种实现方式
1.线程的实现方式 1.用户级线程 开销小,用户空间就可以创建多个。缺点是:内核无法感知用户级多个线程的存在,把其当作只有一个线程,所以只会提供一个处理器。 2.内核级线程 相对于用户级开销稍微大一点,可以利用多…...
Facebook 应用未启用:这款应用目前无法使用,应用开发者已得知这个问题。
错误:Facebook 应用未启用:这款应用目前无法使用,应用开发者已得知这个问题。应用重新启用后,你便能登录。 「应用未经过审核或未发布」: 如果一个应用还没有经过Facebook的审核或者开发者尚未将应用发布,那么它将无法…...
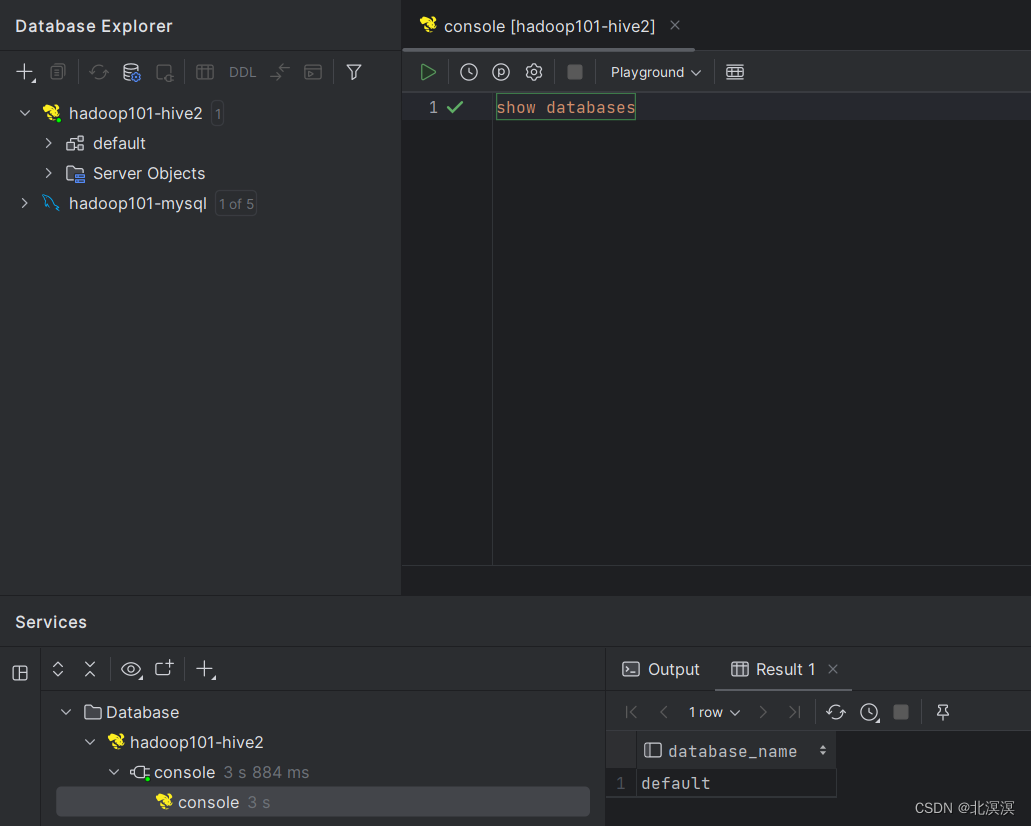
(十八)大数据实战——Hive的metastore元数据服务安装
前言 Hive的metastore服务作用是为Hive CLI或者Hiveserver2提供元数据访问接口。Hive的metastore 是Hive元数据的存储和管理组件,它负责管理 Hive 表、分区、列等元数据信息。元数据是描述数据的数据,它包含了关于表结构、存储位置、数据类型等信息。本…...

ubuntu 22.04 LTS 在 llvm release/17.x 分支上编译 cookbook llvm example Chapter 02
一,从源码编译 llvm 下载源码: $ git clone https://github.com/llvm/llvm-project.git 创建 对应 commit id分支: $ cd llvm-project $ git checkout 5b78868661f42a70fa30 -b 17.x.greater 源码成功编译 llvm-project commit id&…...
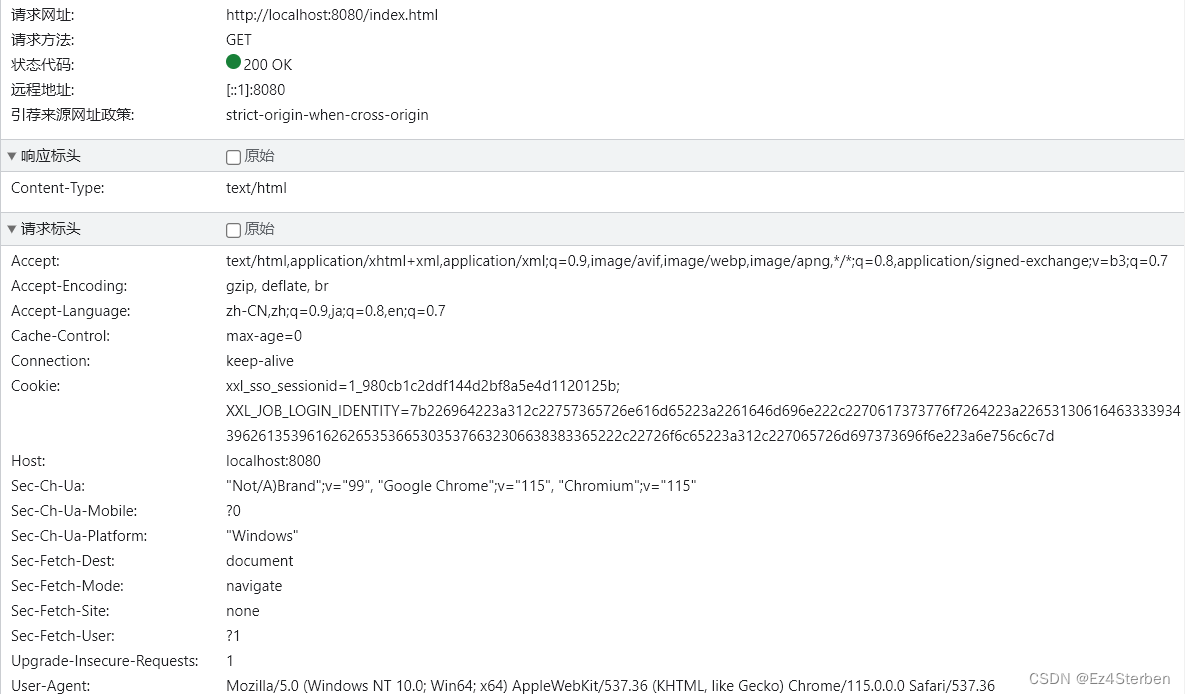
【仿写tomcat】三、通过socket读取http请求信息
仿写tomcat 建立Socket连接获取连接信息查看HTTP信息 建立Socket连接 这里我们也是创建一个专门管理socket的类 package com.tomcatServer.socket;import java.io.*; import java.net.ServerSocket;/*** 套接字存储** author ez4sterben* date 2023/08/15*/ public class Soc…...
Hive的窗口函数与行列转换函数及JSON解析函数
1. 系统内置函数 查看系统内置函数:show functions ; 显示内置函数的用法: desc function lag; – lag为函数名 显示详细的内置函数用法: desc function extended lag; 1.1 行转列 行转列是指多行数据转换为一个列的字段。 Hive行转列用到的函数 con…...

CSS中的z-index属性有什么作用?如何控制元素在层叠上下文中的显示顺序?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ z-index 属性的作用及控制元素层叠顺序作用 ⭐ 控制元素层叠顺序⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅࿰…...
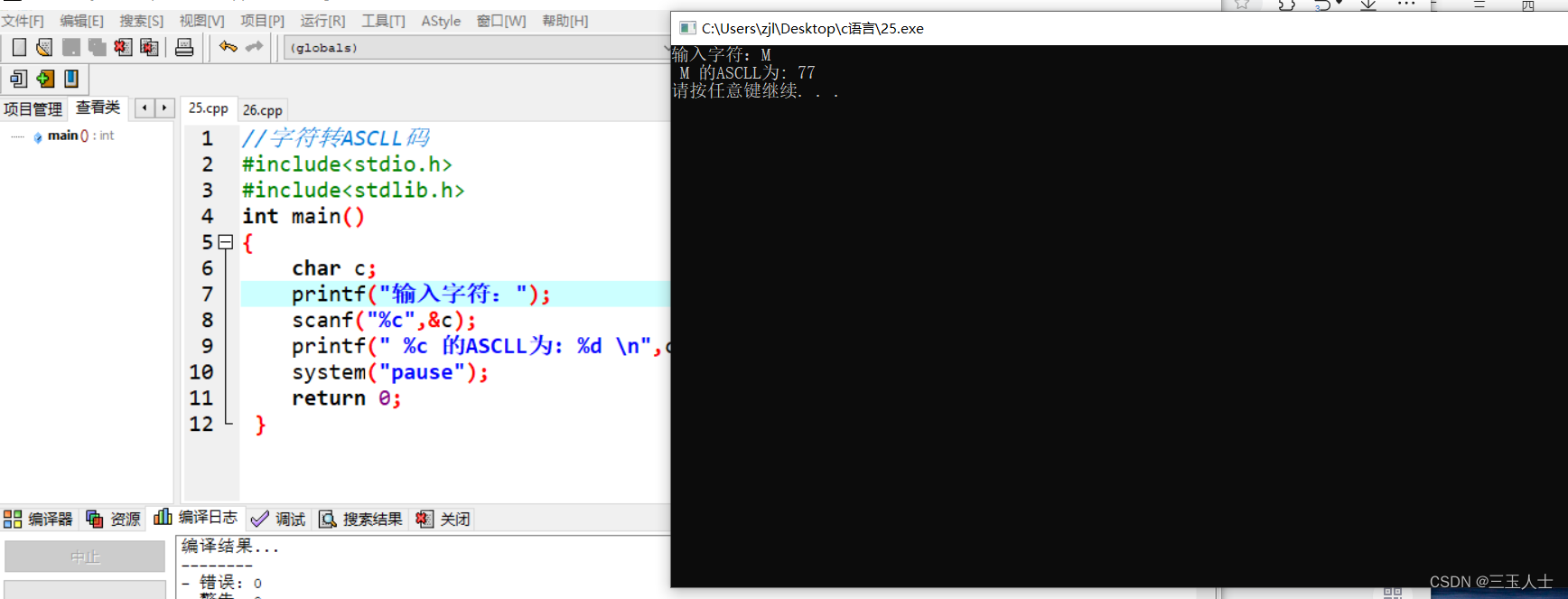
c语言——字符转ASCLL码
//字符转ASCLL码 #include<stdio.h> #include<stdlib.h> int main() {char c;printf("输入字符:");scanf("%c",&c);printf(" %c 的ASCLL为: %d \n",c,c);system("pause");return 0;}...
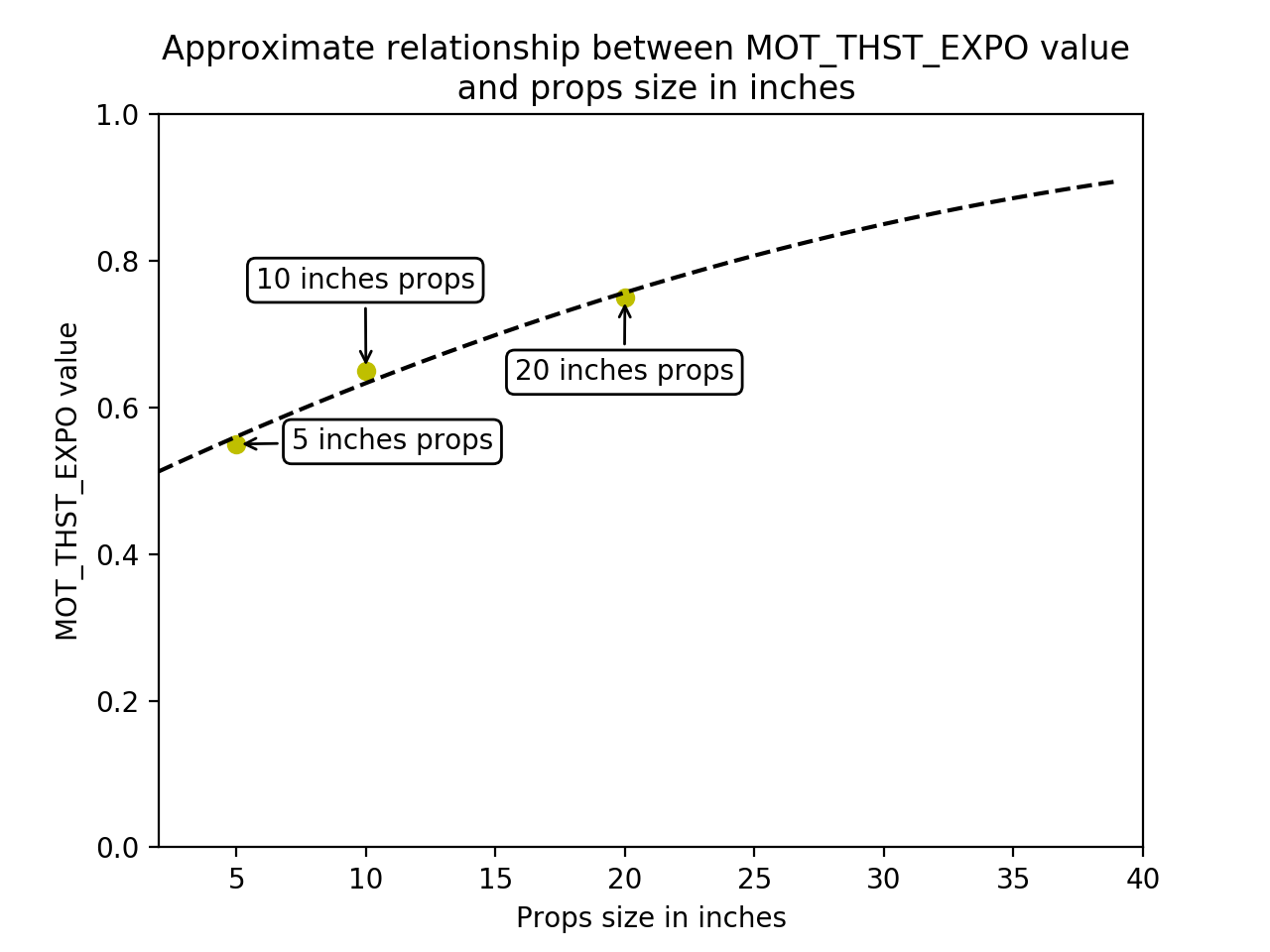
ardupilot开发 --- 安装与调参篇
解锁电机前的安全检查 Pre-arm Safety Checks 安全检查包括:是否未校准、配置或传感器数据是否正确等等,某一项不通过则不允许解锁电机; 目的:防止炸机; 如何禁用这些安全检查?配置 ARMING_CHECKÿ…...

BC108 矩阵交换
描述 KiKi有一个矩阵,他想知道经过k次行变换或列变换后得到的矩阵。请编程帮他解答。 输入描述 第一行包含两个整数n和m,表示一个矩阵包含n行m列,用空格分隔。 (1≤n≤10,1≤m≤10) 从2到n1行,每行输入m个整数(范围-…...

如何发现系统改进点,优化点,提高点,新系统 边界感不要太强
技术人员规划能力,如何规划新的系统_技术规划能力_个人渣记录仅为自己搜索用的博客-CSDN博客 1. 协作中, 双方系统对接, 边界感不要太强. 肯定会不爽, 不爽的点里可以挖掘改进点 肯定会有很多冲突,对方技能欠缺, 对方耽误你的时间, 可以想下有没有什么方案是可…...

5G无人露天矿山解决方案
1、5G无人露天矿山解决方案背景 ①2010.10,国家安监总局《金属非金属地下矿山安全避险“六大系统”安装使用和监督检查暂行规定》 ②2016.03,国家发改委《能源技术革命创新行动计划(2016-2030)》,2025 年重点煤矿区采…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
