chapter 3 Free electrons in solid - 3.2 量子自由电子理论对一些现象的解释
3.2 自由电子气的热容 Heat capacity of free electron gas
3.2.1 计算自由电子的热容 Calculation of Heat Capacity of free Electrons
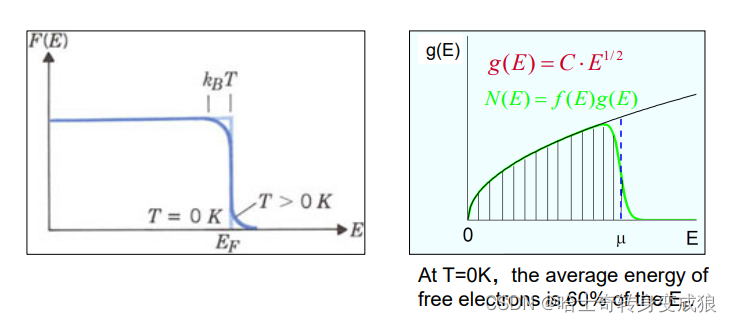
T>0K, total energy of free electrons:
E = ∫ E d N = 3 5 N e E F 0 [ 1 + 5 12 π 2 ( k B T E F 0 ) 2 ] E= \int EdN = \frac{3}{5} N_e E_F^0 [1+\frac{5}{12}\pi^2 (\frac{k_B T}{E_F^0})^2] E=∫EdN=53NeEF0[1+125π2(EF0kBT)2]
C V e = ∂ E ∂ T = γ T C_V^e = \frac{\partial E}{\partial T} = \gamma T CVe=∂T∂E=γT
γ = π 2 N e k B 2 2 E F 0 , N e = N Z \gamma = \frac{\pi^2 N_e k_B^2}{2E_F^0},\ \ N_e = NZ γ=2EF0π2NekB2, Ne=NZ
N e N_e Ne: 自由电子数 the total number of free electrons
N: 原子数 the number of atoms
Z: 每个原子提供的价电子数 the number of free electrons provided by one atom
3.2.2 电子热容与声子热容的对比 Comparison of C V e C_V^e CVe and C V l C_V^l CVl
The total heat capacity of a metal includes electron contribution and phonon contribution:
C V = C V e + C V l C_V = C_V^e +C_V^l CV=CVe+CVl
high temperature ( T > Θ D T > \Theta_D T>ΘD): C V e ≪ C V l , C V ≈ C V l C_V^e\ll C_V^l,\ \ C_V \approx C_V^l CVe≪CVl, CV≈CVl
low temperature ( T ≪ Θ D T \ll \Theta_D T≪ΘD): C V = C V e + C V l = γ T + b T 3 C_V = C_V^e + C_V^l = \gamma T+b T^3 CV=CVe+CVl=γT+bT3
3.2.3 固体热容 Heat Capacity of Metal
At low temperature, the electronic contribution may be comparable with the phonon’s contribution.
低温物理中,电子热熔具有重要意义。
C V M e t a l = { C V P h o n o n = b T 3 C V E l e c t r o n = γ T C_V^{Metal}= \begin{cases} C_V^{Phonon} = bT^3 \\ C_V^{Electron} = \gamma T \end{cases} CVMetal={CVPhonon=bT3CVElectron=γT
3.3 电子传输特性 Transport properties of conductive electron
3.3.1 电导率与温度的关系Electrical conductivity vs Temperature
根据德鲁德自由电子模型: σ ∝ T − 1 / 2 \sigma \propto T^{-1/2} σ∝T−1/2
实验结果表明: σ ∝ T − 1 \sigma \propto T^{-1} σ∝T−1
What is the key factor affecting the theoretical electrical conductivity of metals?
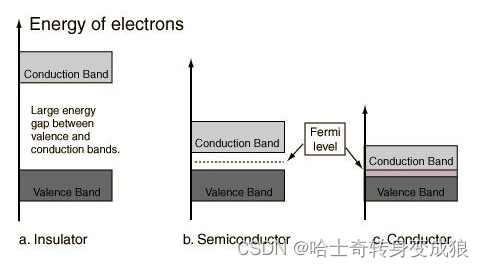
Electrical conductivity depends on the DOS at E F E_F EF and the size of the Fermi surface. —Related to its crystal structure and its valent electrons!
影响金属理论电导率的关键因素:态密度和费米面的大小—与晶体结构和价电子有关!
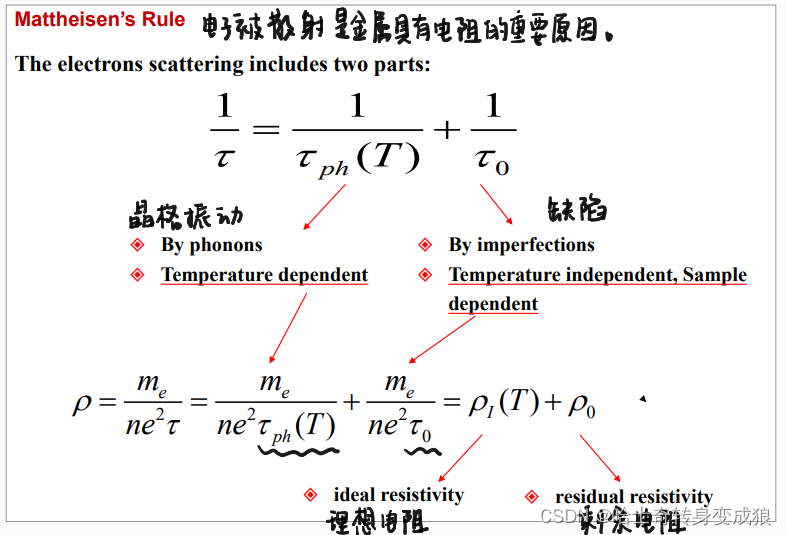
根据德鲁德模型: σ = n e 2 m τ \sigma =\frac{ne^2}{m}\tau σ=mne2τ
经典理论中, τ \tau τ与温度无关。
τ = 平均自由程 l v R M S \tau = \frac{平均自由程l}{v_{RMS}} τ=vRMS平均自由程l,而 1 2 v ˉ 2 = 3 2 k B T \frac{1}{2}\bar v^2 =\frac{3}{2}k_BT 21vˉ2=23kBT,所以 σ ∝ T − 1 / 2 \sigma \propto T^{-1/2} σ∝T−1/2
根据量子力学的观点,对外界电场产生响应的仅仅为费米能附近的电子,这里的速度 v R M S v_{RMS} vRMS应当为费米速度,而费米速度与温度无关,因此关键在于平均自由程与温度的关系。
晶体中的电子具有波粒二象性,波长不满足布拉格定律,所以电子不会与离子实发生碰撞,而是自由传播(索末菲模型与德鲁德模型之间的差异)。对于理想晶体,电子波在晶体中畅行无阻, l = ∞ l=\infty l=∞。由于晶体缺陷和晶格振动, l ∝ T − 1 l \propto T^{-1} l∝T−1,所以 σ ∝ T − 1 \sigma \propto T^{-1} σ∝T−1。
Mattheisen’s Rule
3.3.2 导热系数 Thermal conductivity
Electrons’ Heat Transport
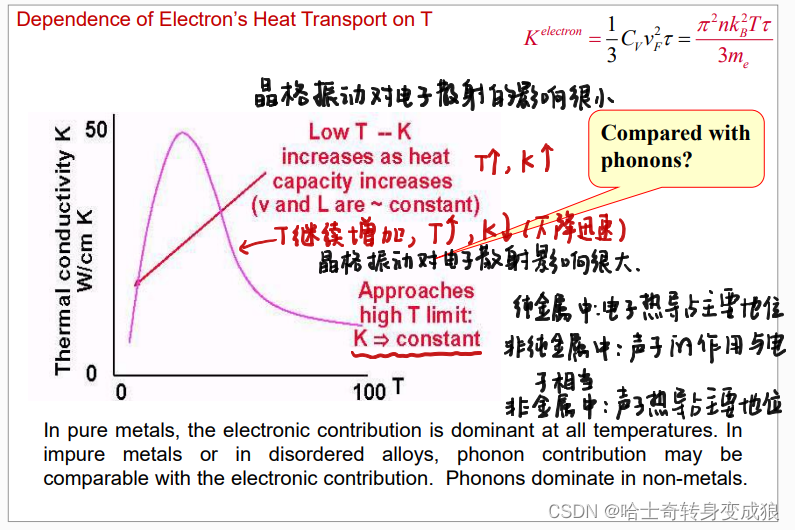
电子热导: K e l e c t r o n = 1 3 C V e ⋅ v ⋅ l = 1 3 C V e ⋅ v F 2 ⋅ τ = π 2 n k B T τ 3 m e K^{electron} = \frac{1}{3}C_V^e \cdot v \cdot l =\frac{1}{3}C_V^e \cdot v_F^2 \cdot \tau = \frac{\pi^2 n k_B T \tau}{3m_e} Kelectron=31CVe⋅v⋅l=31CVe⋅vF2⋅τ=3meπ2nkBTτ
声子热导: K p h o n o n = 1 3 C V l ⋅ v 0 ⋅ λ K^{phonon} = \frac{1}{3}C_V^l \cdot v_0 \cdot \lambda Kphonon=31CVl⋅v0⋅λ
电子热容比声子热容小两个数量级,但费米速度比 v 0 v_0 v0大三个数量级,所以电子热导大于声子热导
The speed of conductive electrons is in the Fermi velocity, which is much higher than that of phonons.
热流密度: J t h e r m a l = − K d T d x J_{thermal} = -K\frac{dT}{dx} Jthermal=−KdxdT
K m e t a l s ≫ K n o n − m e t a l s K_{metals} \gg K_{non-metals} Kmetals≫Knon−metals
3.3.3 魏德曼·弗朗兹定理 Wiedemann-Franz Law
In physics, the Wiedemann–Franz law states that the ratio of the electronic contribution to the thermal conductivity (κ) and the electrical conductivity (σ) of a metal is proportional to the temperature (T).
电导率高,热导率也高。
K σ = L T \frac{K}{\sigma} = LT σK=LT
L:洛伦兹常数,The proportionality constant L is known as the Lorentz number
理论值: L = 2.45 × 1 0 − 8 ( V / K ) 2 L= 2.45\times 10^{-8}(V/K)^2 L=2.45×10−8(V/K)2
K e σ = π 2 3 ( k B e ) 2 T \frac{K_e}{\sigma} = \frac{\pi^2}{3}\left (\frac{k_B}{e} \right)^2 T σKe=3π2(ekB)2T
3.3.4 霍尔效应 Hall effect
In a conductor, an associated electric field (Hall field) is built in the direction J×B when a current J flows across a magnetic field B.
在导体中,当电流J流过磁场B时,会在J×B方向上产生相关的电场(霍尔场)。
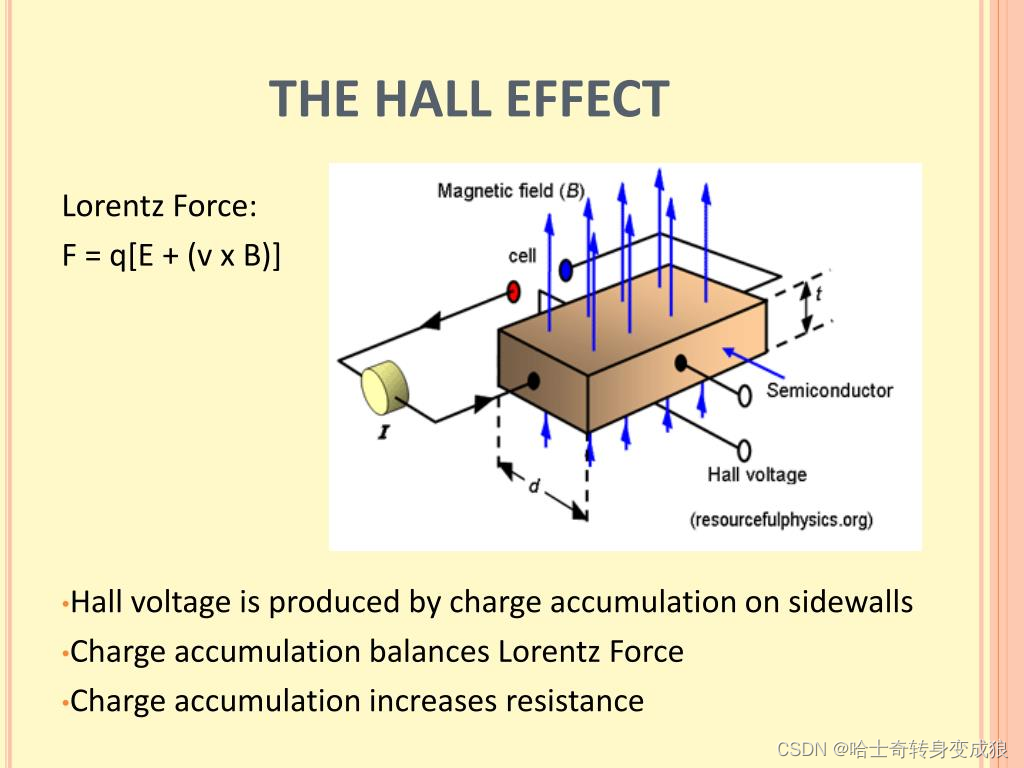
Lorentz force causes the deflection of electrons and then accumulate electrons on one face of the conductor. At stable state, the electrostatic force of Hall field just cancels the Lorentz force duo to magnetic field.
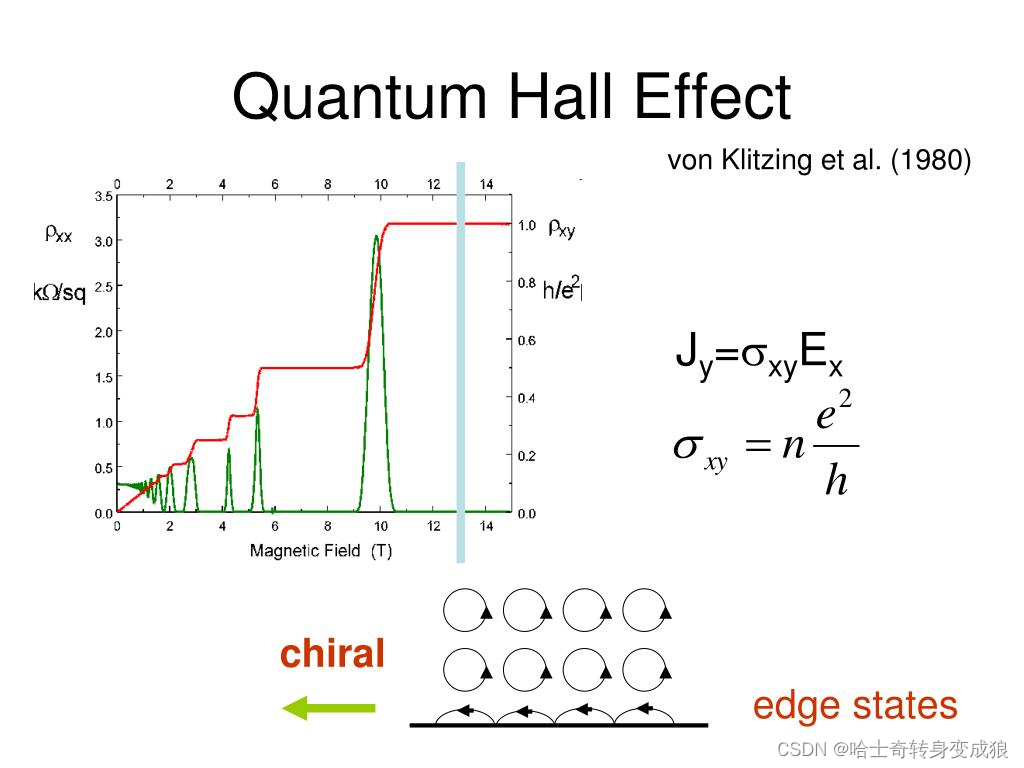
Quantum Hall Effect
In 1985 Klaus von Klitzing won the Nobel Prize for discovery of the quantized Hall effect. In a two-dimensional metal or semiconductor, the Hall effect is also observed, but at low temperatures a series of steps appear in the Hall resistance as a function of magnetic field instead of the monotonic increase. What is more, these steps occur at incredibly precise values of resistance which are the same no matter what sample is investigated. The resistance is quantized in units of h / e 2 h/e^2 h/e2 divided by an integer. This is the QUANTUM HALL EFFECT.
3.4 电子发射与接触电势 Electron emission and contacting voltage
电子发射:电子脱离材料的束缚成为自由电子
- 冷发射Cold electron emission:low pressure , high voltage(尖端放电,场发射)
- 热发射Thermal electron emission: high temperature (高温热钨电镜)
功函数 work function:每个电子脱离晶体发射出来需要的能量the amount of energy per electron is required to emit (i.e. removing from a material). (Analogous to ionization potential)
The work functions of metals change with the temperature.
W = ϕ = V 0 − E F W = \phi = V_0 -E_F W=ϕ=V0−EF
W ~ several eV
V 0 V_0 V0: free electron energy in vacuum
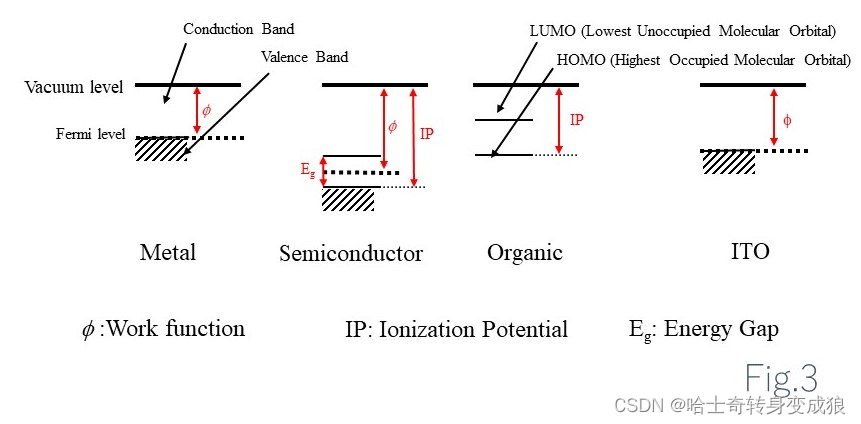
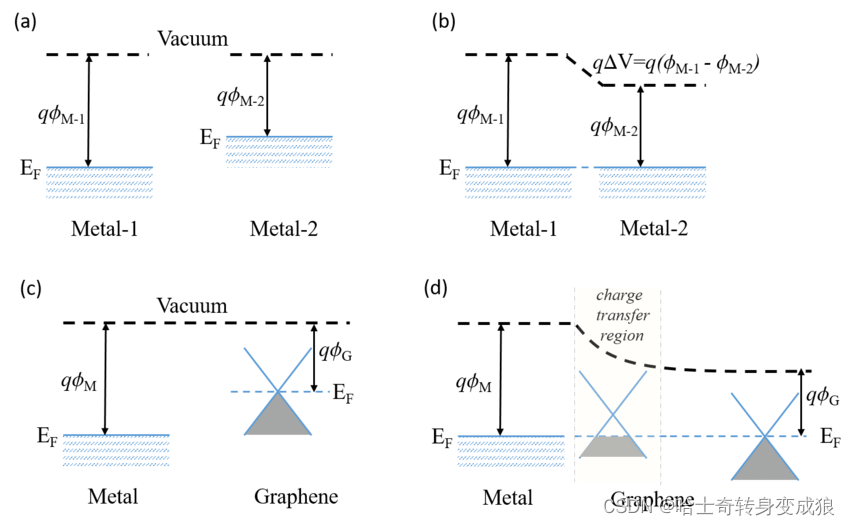
接触电势 contacting voltage:两个不同材料相接触,在界面上产生接触电势
费米能不同,电子自发跃迁,在同一系统中拉平费米能,进而去研究。
接触电势差等于两种材料的功函数之差除以e。
V 12 = 1 e ( W 2 − W 1 ) = 1 2 ( E 1 F − E 2 F ) V_{12}= \frac{1}{e} (W_2 - W_1) = \frac{1}{2}(E_{1F} - E_{2F}) V12=e1(W2−W1)=21(E1F−E2F)
相关文章:

chapter 3 Free electrons in solid - 3.2 量子自由电子理论对一些现象的解释
3.2 自由电子气的热容 Heat capacity of free electron gas 3.2.1 计算自由电子的热容 Calculation of Heat Capacity of free Electrons T>0K, total energy of free electrons: E ∫ E d N 3 5 N e E F 0 [ 1 5 12 π 2 ( k B T E F 0 ) 2 ] E \int EdN \frac{3}{5}…...

vue实现打印功能
在Vue应用中调用打印机功能,可以使用JavaScript的window.print()方法。这个方法会打开打印对话框,然后让我们选择打印设置并打印文档,但是尼这种方法依赖于浏览器的打印功能。 以下是一个简单的示例,演示如何在Vue组件中调用打印…...

golang—面试题大全
目录标题 sliceslice和array的区别slice扩容机制slice是否线程安全slice分配到栈上还是堆上扩容过程中是否重新写入go深拷贝发生在什么情况下?切片的深拷贝是怎么做的copy和左值进行初始化区别slice和map的区别 mapmap介绍map的key的类型map对象如何比较map的底层原…...

Spring、Springboot、SpringCloud--包含的知识点大全
类型难度AOPspring-自定义AOP面向切面注解--统一切面处理-登陆信息采集快速入门SpringbootAOP实现切面处理请求Demo线程池通俗易懂的线程池底层原理,一文知所有数据结构数据结构-链表篇数据结构--数组篇数据结构之-concurrentHashMap源码分析JVMJVM调优及各种问题处…...
MongoDB:数据库初步应用
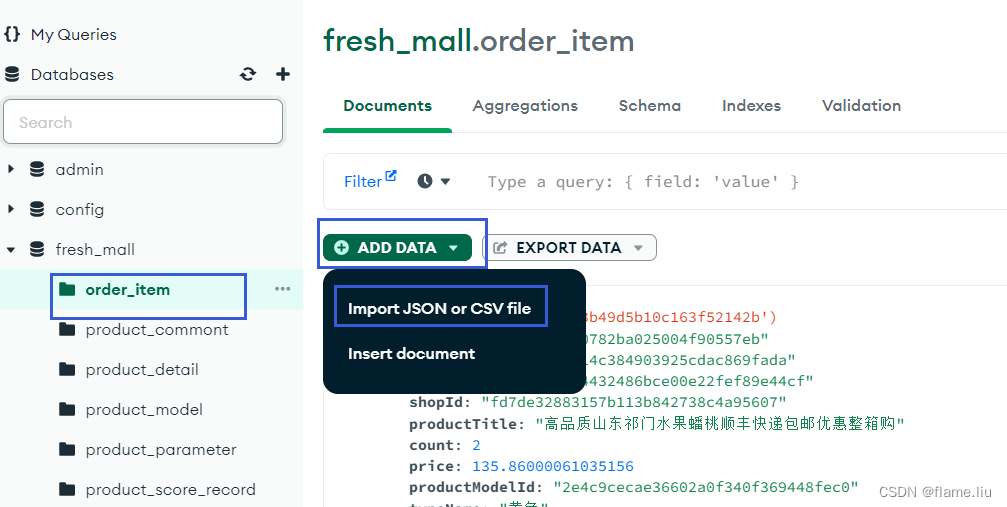
一.连接MongoDB 1.MongoDBCompass连接数据库 连接路径:mongodb://用户名:密码localhost:27017/ 2.创建数据库(集合) MongoDB中数据库被称为集合. MongoDBCompass连接后,点击红色框加号创建集合,点击蓝色框加号创建文档(数据表) 文档中的数据结构(相当于表中的列)设计不用管…...

C#之枚举中的按位与()按位或(|)。
一些基础定义: 按位或运算符(|)是一种位运算符,用来对两个二进制数进行操作。对于每个位上的1,如果至少有一个二进制数中的对应位为1,则结果为1;否则,结果为0。按位与运算符&#x…...
Blazor前后端框架Known-V1.2.12
V1.2.12 Known是基于C#和Blazor开发的前后端分离快速开发框架,开箱即用,跨平台,一处代码,多处运行。 Gitee: https://gitee.com/known/KnownGithub:https://github.com/known/Known 概述 基于C#和Blazo…...

bug记录:微信小程序 给button使用all: initial重置样式
场景:通过uniapp开发微信小程序 ,使用uview的u-popup弹窗,里面内嵌了一个原生button标签,因为微信小程序的button是有默认样式的,所以通过all: initial重置样式 。但是整个弹窗的点击事件都会被button上面的点击事件覆…...
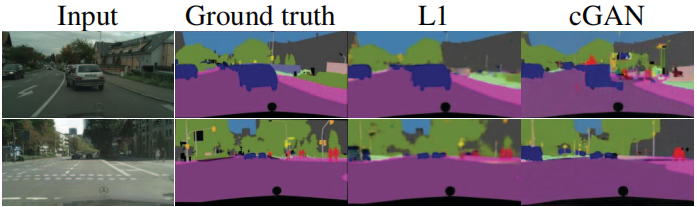
【计算机视觉|生成对抗】带条件的对抗网络进行图像到图像的转换(pix2pix)
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:Image-to-Image Translation with Conditional Adversarial Networks 链接:Image-to-Image Translation with Conditional Adversarial Networks | IEEE Conference Publicati…...

[时序数据库]:InfluxDB进阶
文章目录 1 摘要2 背景2.1 问题一:针对Influx V2.0工具2.2 问题二:针对Influx查询语言 3 需求分析4 快速入门4.1 客户端驱动版本选择4.2 连接influx4.2.1 influx配置信息4.2.2 influx连接配置4.2.3 测试连通情况 5 Influx工具类5.1 InfluxQL工具类5.1.1 …...
uniapp编写微信小程序遇到的坑总结
1、阻止事件冒泡 使用uniapp开发微信小程序的时候,发现使用click.stop来阻止事件冒泡没有作用,点击了之后发现仍然会触发父组件或者祖先组件的事件。 在网上查阅,发现使用tap.stop才能阻止事件冒泡。 2、二维码生成 在网上找了很多&…...

Binary operator ‘*‘ cannot be applied to two ‘Double?‘ operands
在 swift 中声明 Double 类型参数变量在进行运算处理时抛出了如下异常 Binary operator * cannot be applied to two Double? operands 情况一 参数类型不匹配,需将参数类型进行匹配 self.max height / (length * width) // 初始 self.max height / (length * Double(wid…...
C#如何打包EXE程序生成setup安装文件
项目结束之后,有需要将winForm程序打包成.exe文件提供给用户。 这里记录一下打包过程。 1:首先获取打包插件,如果你的VS已经安装,忽略此步骤。 点击 工具->扩展和更新,选择联机,搜索installer&#x…...

【python实现向日葵控制软件功能】手机远程控制电脑
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人_python人工智能视觉(opencv)从入门到实战,前端,微信小程序-CSDN博客 最新的uniapp毕业设计专栏也放在下方了: https://blog.csdn.net/lbcy…...

手机系统录屏怎么录?有什么其他录制方法和注意事项?
手机系统录屏是一种很方便的方式,可以用于录制游戏、教程视频,或者是跟别人分享一些操作。在不同的手机系统中,录制方法可能会有所不同,以下是一些通用的步骤分享以及其他录制工具的分享,有需要的小伙伴们快来看一看吧…...
记录一个编译TubeTK时的报错:at_check问题
在使用如下命令安装TubeTK的cuda_nms时,报了一个错误,记录一下这个错误和解决办法 (base) redmeryredmery:~/Desktop/MOT/TubeTK/post_processing/nms$ python setup.py build_ext --inplace因为这个命令是在/home/redmery/Desktop/MOT/TubeTK/install/…...

k8s v1.27.4二进制部署记录
记录二进制部署过程 #!/bin/bash#升级内核 update_kernel() {rpm --import https://www.elrepo.org/RPM-GPG-KEY-elrepo.orgyum -y install https://www.elrepo.org/elrepo-release-7.el7.elrepo.noarch.rpmyum --disablerepo"*" --enablerepo"elrepo-kernel&q…...

C# API 文档注释规范
C# API 文档注释规范 1. 命名空间注释(namespace)2. summary3. remarks and para4. param5. returns6. example and code7. exception8. typeparam 最近在开发工作中需要实现 API 帮助文档,如果根据所写的代码直接重写 API 帮助文档将会是意见非常大的工作量&#x…...
分类预测 | Matlab实现基于TSOA-CNN-GRU-Attention的数据分类预测
分类预测 | Matlab实现基于TSOA-CNN-GRU-Attention的数据分类预测 目录 分类预测 | Matlab实现基于TSOA-CNN-GRU-Attention的数据分类预测效果一览基本介绍研究内容程序设计参考资料 效果一览 基本介绍 Matlab实现分类预测 | Matlab实现基于TSOA-CNN-GRU-Attention的数据分类预…...

《深度剖析K8s》学习笔记
一、容器技术 1.从进程说起 a. 概述 进程:数据和状态的综合 容器技术的核心:约束和修改进程的动态表现,创造出边界(Cgroup:约束/namespace:进程视图) 启动容器例子: docker ru…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...