Codeforces Round 881 Div.3
文章目录
- 贪心:A. Sasha and Array Coloring
- 结论:B. Long Long
- 性质:C. Sum in Binary Tree
- dfs求叶子数量:D. Apple Tree
- 二分与前缀和:E. Tracking Segments
贪心:A. Sasha and Array Coloring
Problem - A - Codeforces
将数组中的每个数染色,同一颜色的数字中,将最大值与最小值相减得到分数,问:所有的染色方案中,总分最高是多少
显然,同一颜色的数字除了最大和最小,其他的数没有用,要使总分最高,同一颜色的数字要最少,最少为两个
将数组的最大与最小相减得到分数,再将次大与次小相减…
#include <iostream>
#include <algorithm>
using namespace std;const int N = 55;
int a[N], T;int main()
{cin >> T;while ( T -- ){int n, sum = 0;cin >> n;for (int i = 0; i < n; ++ i ) cin >> a[i];sort(a, a + n);int l = 0, r = n - 1;while (l < r){sum += (a[r] - a[l]);l ++ , r -- ;}cout << sum << endl;}return 0;
}
结论:B. Long Long

sum一定是所有数绝对值之和
结论:最少操作次数等于连续负数子段个数,所有统计连续非负的子段数量即可
#include <iostream>
#include <cmath>
using namespace std;typedef long long LL;
const int N = 2e5 + 10;
int a[N], T;int main()
{cin >> T;while ( T -- ){LL n, sum = 0, cnt = 0;cin >> n;for (int i = 0; i < n; ++ i) {cin >> a[i];sum += abs(a[i]);}for (int i = 0; i < n;){if (a[i] < 0){cnt ++ ;while (i < n && a[i] <= 0) i ++ ;}else i ++ ;}cout << sum << ' ' << cnt << endl;}return 0;
}
debug:ans要开LL,wa了4发,非负子段中可以出现0,所以a[i] < 0是不行的
性质:C. Sum in Binary Tree
Problem - C - Codeforces
[外链图片转存中…(img-XlnHbBnn-1692359176162)]
一颗完全二叉树,根节点编号为1号,问根节点到n号节点的编号之和
手写堆时,学过:孩子的编号 / 2为父亲的编号,父亲的编号 * 2,或* 2 + 1能得到左右孩子的编号
若从1开始走到n,路径是无法一次确定的。从n走到1,路径能一次确定。所以将n不断/2,就能走到根节点,过程中维护sum即可
#include <iostream>
using namespace std;typedef long long LL;int main()
{int T;cin >> T;while ( T -- ){LL sum = 0, n;cin >> n;while (n){sum += n;n /= 2;}cout << sum << endl;}return 0;
}
dfs求叶子数量:D. Apple Tree
Problem - D - Codeforces
对于所有节点1~n,求以每个节点为根节点时,子树中叶子节点的数量leaf[i]
答案为leaf[x] * leaf[y]
用dfs求叶子节点的数量,有两个坑:树要建无向边,一开始我自以为是有向边,方向从根节点向下,但通过用例就能看出这是无向边
其次,无向树较难实现在线求叶子节点数量,一开始我写的是有向树,用dfs在线求叶子节点数量很好实现。但是无向树想要在线求,有一个问题,dfs会向根节点遍历,虽然能特判根节点不是叶子,但是dfs会遍历到不属于当前子树的叶子
解决方法是:用根节点开始dfs,用leaf数组保存每颗子树的叶子节点,从其他节点开始地离线求法依然是错的,只能从根节点开始求
#include <iostream>
#include <cstring>
using namespace std;typedef long long LL;
const int N = 2e5 + 10, M = 4e5 + 10;
int h[N], e[M], ne[M], idx;
int T, n, Q;
int leaf[N];void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}int dfs(int x, int fa)
{bool flag = true;int cnt = 0;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (y != fa) flag = false, leaf[x] += dfs(y, x);}if (flag) leaf[x] = 1; return leaf[x];
}int main()
{cin >> T;while ( T -- ){memset(h, -1, sizeof h);memset(leaf, 0, sizeof leaf);idx = 0;cin >> n;int x, y;for (int i = 0; i < n - 1; ++ i ){cin >> x >> y;add(x, y), add(y, x);}cin >> Q;dfs(1, -1);while ( Q -- ){cin >> x >> y;cout << (LL)leaf[x] * leaf[y] << endl;}}return 0;
}
二分与前缀和:E. Tracking Segments
Problem - E - Codeforces
每次做二分题脑子都转不过来,要将边界问题考虑得很清楚
首先,分析题意:一个元素全为0的数组,给定m个区间与q个操作,每次操作将某个元素置为1,问第几次操作时,m个区间中至少有一个区间的1的数量大于0的数量
可以看出这题具有二段性,由于每次操作都是将0置为1,所以整个数组中1的数量随着操作次数增加。假设答案为ans,进行ans次操作后,有一个区间的1数量大于0数量。那么在之后的操作中,1的数量只增不减。所以对于第 [ a n s , m ] [ans, m] [ans,m]次操作,至少有1个区间的1数量大于0数量
而在进行第 [ 1 , a n s − 1 ] [1, ans-1] [1,ans−1]次操作时,所有区间1的数量一定小于0的数量,操作次数呈现两段性
根据操作次数 [ 1 , q ] [1, q] [1,q]的两段性,我们可以二分出两段区间的分界点,即最终答案ans
每次check时,进行mid次操作,遍历所有区间,只要有区间的1数量大于0数量,check就返回true。说明mid落在了右半段区间,r = mid。若check为false,说明mid落在左半区间,l = mid + 1
什么情况下会无解?进行了q次操作后,依然没有一个区间的1数量大于0数量,此时无解。那么无解时,会二分到哪个答案?因为操作次数的范围为 [ 1 , q ] [1, q] [1,q],所以无解时操作次数为 q + 1 q + 1 q+1
因此二分的区间需要设置为 [ 1 , q + 1 ] [1, q + 1] [1,q+1],当最后的结果为 q + 1 q + 1 q+1时,无解
用前缀和求区间中1的数量
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e5 + 10;
int n, m;
int a[N], T, Q, L[N], R[N], change[N];bool check(int mid)
{for (int i = 1; i <= m; ++ i) {int ones = a[R[i]] - a[L[i] - 1];if (2 * ones > R[i] - L[i] + 1) return true;}return false;
}int main()
{cin >> T;while ( T -- ){cin >> n >> m;for (int i = 1; i <= m; ++ i ) cin >> L[i] >> R[i];cin >> Q;for (int i = 1; i <= Q; ++ i ) cin >> change[i]; int l = 0, r = Q + 1;while (l < r){int mid = l + r >> 1;memset(a, 0, sizeof a);for (int i = 1; i <= mid; ++ i ) a[change[i]] = 1;for (int i = 1; i <= n; ++ i ) a[i] += a[i - 1];if (check(mid)) r = mid;else l = mid + 1;}if (r == Q + 1) puts("-1");else cout << r << endl;}return 0;
}
debug:check要建立所有的区间,所以for循环中,i <= m,我写成了i <= mid,WA两发
i <= mid应该是枚举操作时的条件
剩下两题有些难,20号之后回来补
相关文章:

Codeforces Round 881 Div.3
文章目录 贪心:A. Sasha and Array Coloring结论:B. Long Long性质:C. Sum in Binary Treedfs求叶子数量:D. Apple Tree二分与前缀和:E. Tracking Segments 贪心:A. Sasha and Array Coloring Problem - A…...
从入门到精通系列之十六:linux服务器安装minikube的详细步骤)
Kubernetes(K8s)从入门到精通系列之十六:linux服务器安装minikube的详细步骤
Kubernetes K8s从入门到精通系列之十六:linux服务器安装minikube的详细步骤 一、安装Docker二、创建启动minikube用户三、下载minikube四、安装minikube五、将minikube命令添加到环境变量六、启动minikube七、查看pods,自动安装kubectl八、重命名minikube kubectl --为kubect…...
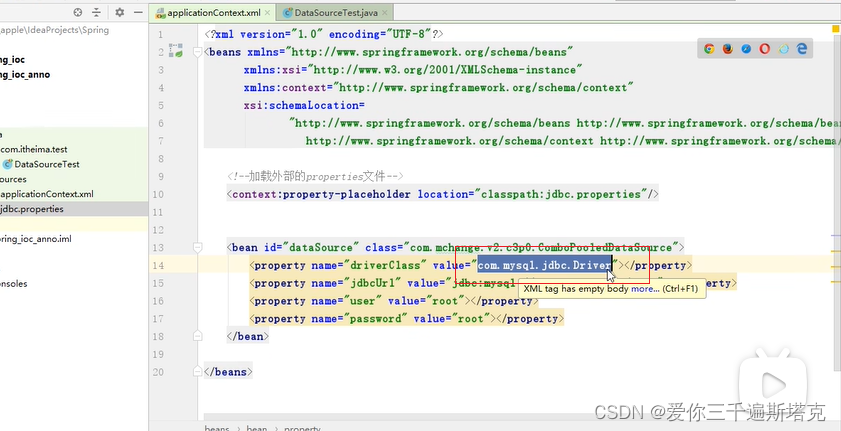
JDBC配置文件抽取-spring11
改成context,到这里我们context命名空间就引入完毕,加载我们外部properties配置文件: 用它:第一个属性,第二个类型 在未加载路径下: 现在我已经把spring加载到配置文件里了。 现在我需要在这个位置引入proper…...

el-form组件相关的一些基础使用
el-checkbox 01.description 多选单选框 02.场景举例 需要对每一条数据展示她的某些状态是否存在 03.代码展示 <el-checkbox v-model"query.isAutoAccptncsign" true-label1 false-label0 :disabled"ifReview?true:false">自动发起承兑应答</…...
全新 – Amazon EC2 M1 Mac 实例
去年,在 re: Invent 2021 大会期间,我写了一篇博客文章,宣布推出 EC2 M1 Mac 实例的预览版。我知道你们当中许多人请求访问预览版,我们尽了最大努力,却无法让所有人满意。不过,大家现在已经无需等待了。我很…...

java # Servlet
一、什么是Servlet? Servlet是javaEE规范之一。规范就是接口。JavaWeb三大组件分别是:Servlet程序、Filter过滤器、Listener监听器。Servlet是运行在服务器上的一个Java小程序,它可以接收客户端发送来的请求,并响应数据给客户端。…...

Linux内核的两种安全策略:基于inode的安全与基于文件路径的安全
实现系统安全的策略 在Linux中,一切且为文件,实现系统安全的策略主要可分为两种:基于inode的安全、基于文件路径的安全。 基于inode的安全 为文件引入安全属性,安全属性不属于文件内容,它是文件的元数据,…...

有哪些前端开发工具推荐? - 易智编译EaseEditing
在前端开发中,有许多工具可以帮助你更高效地进行开发、调试和优化。以下是一些常用的前端开发工具推荐: 代码编辑器/集成开发环境(IDE): Visual Studio Code:功能强大、轻量级的代码编辑器,支…...

【JAVA】抽象类与接口
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈Java 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 抽象类与接口 1. 抽象类1.1 抽象类的概念…...

人脸图像处理
1,人脸图像与特征基础 人脸图像的特点 规律性: 人的两只眼睛总是对称分布在人脸的上半部分,鼻子和嘴唇中心点的连线基本与两眼之间的连线垂直,嘴绝对不会超过眼镜的两端点(双眼为d,则双眼到嘴巴的垂直距离一般在0.8-1.25) 唯一性 非侵扰与便利性 可扩展性 人脸图像的应用 身份…...

Docker入门——实战图像分类
一、背景 思考: 在一个项目的部署阶段,往往需要部署到云服务器或者是终端设备上,而环境的搭建往往是最费时间和精力的,特别是需要保证运行环境一致性,有什么办法可以批量部署相同环境呢? Docker本质——…...

【HarmonyOS北向开发】-02 第一个程序测试
飞书原文档链接:Docs...

关于小程序收集用户手机号行为的规范
手机号在日常生活中被广泛使用,是重要的用户个人信息,小程序开发者应在用户明确同意的前提下,依法合规地处理用户的手机号信息。 而部分开发者在处理用户手机号过程中,存在不规范收集行为,影响了用户的正常使用体验&a…...

js判断手指的上滑,下滑,左滑,右滑,事件监听 和 判断鼠标滚轮向上滚动滑轮向下滚动
js判断手指的上滑,下滑,左滑,右滑,事件监听 和 判断鼠标滚轮向上滚动滑轮向下滚动 pc端 判断鼠标滚轮向上滚动滑轮向下滚动 const scrollFunc (e) > { e e || window.event; let wheelDelta e.wheelDelta ? e.wheelDelta…...

ES 一些简单 的查询注意事项
term query 不分词字段 带分数 where namexxx filter 分词字段 不分词字段 不带分数 Terms query 所有类型 带分数 where name in(xxx) Range query where name between xxx and xxx Exists Regexp Match query 分词字段/基础字段 Multi-match query 多个分词字段/基础字段 Boo…...

LeetCode //C - 57. Insert Interval
57. Insert Interval You are given an array of non-overlapping intervals intervals where intervals[i] [ s t a r t i , e n d i start_i, end_i starti,endi] represent the start and the end of the i t h i^{th} ith interval and intervals is sorted in asce…...

android手势事件
与手势事件有关的方法 dispatchTouchEvent():该方法将触摸事件分发给相应的视图或视图组。onInterceptTouchEvent():该方法用于判断是否需要拦截触摸事件,如果需要拦截,则返回 true,否则返回 false。onTouchEvent()&a…...
)
[网络安全学习篇01]:windowsxp、windows2003、windows7、windows2008系统部署(千峰网络安全视频笔记)
VM 虚拟机:VMware Workstation 15.5 PRO(建议升至最高版本) 部署windows-xp系统 一、配置虚拟机硬件并安装系统 1、在VMware文件目录下创建一个空文件夹将其命名位:winxp-1 2、打开VMware软件,点击创建新的虚拟机。…...
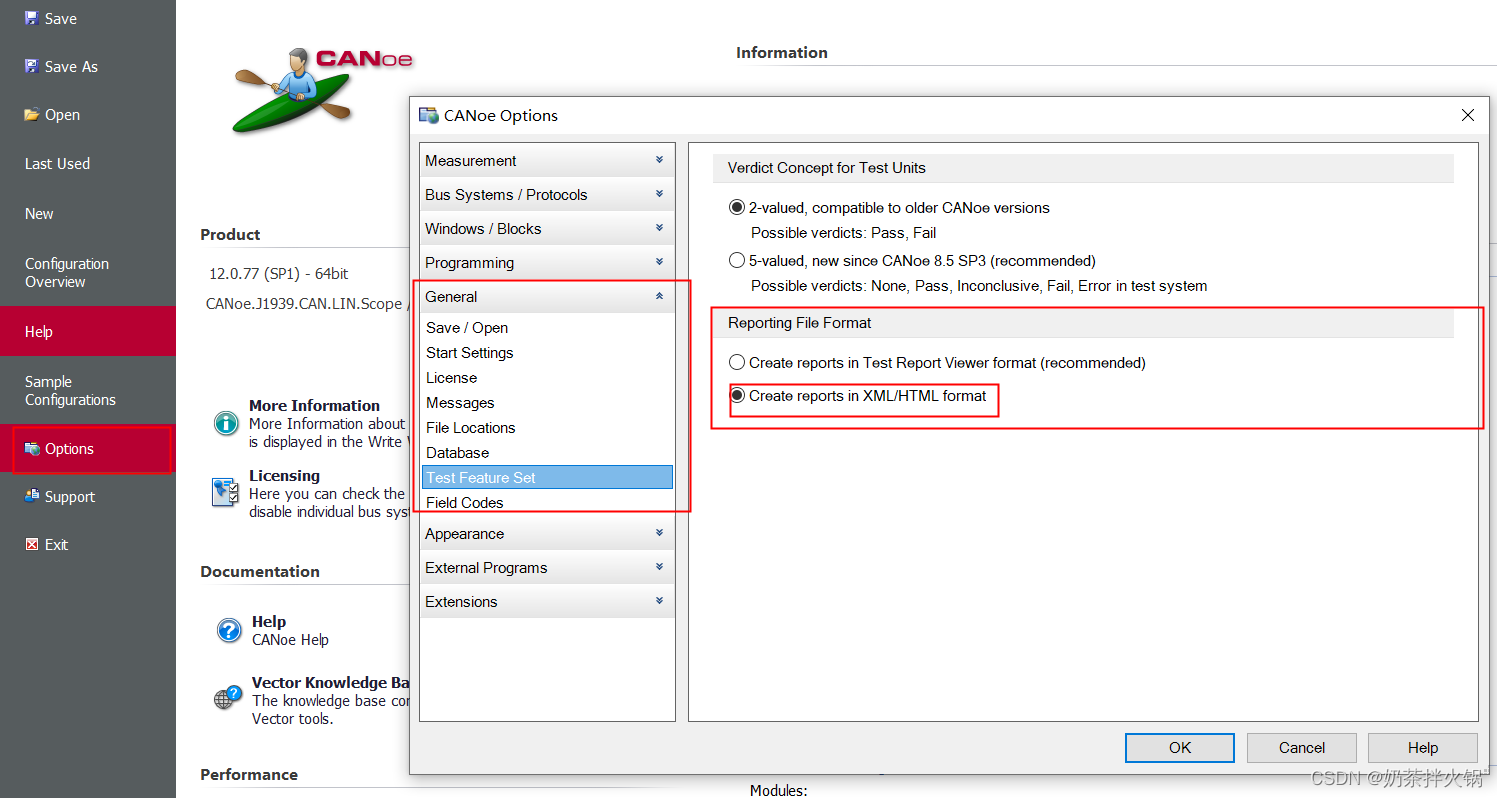
CANoe自动化工程的搭建
基于XMLCAPL建立自动化工程 1、导入ini文件2、新建 Test Environment3、报告类型4、代码编写 1、导入ini文件 工程的配置的文件,配置DUT相关信息,具体视工程而编写内容。 2、新建 Test Environment 1、新建XML测试用例环境 2、导入XML测试用例文件 …...

第6章:支持向量机
间隔与支持向量 w为法向量,决定的是超平面的方向。b是偏移项,决定了超平面与原点之间的距离。 为什么最大化间隔,得到的就是最优平面呢? 当超平面没有正确划分正负样本时,几何间隔为负数。几何间隔,各个…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
