LeetCode450. 删除二叉搜索树中的节点
450. 删除二叉搜索树中的节点
文章目录
- [450. 删除二叉搜索树中的节点](https://leetcode.cn/problems/delete-node-in-a-bst/)
- 一、题目
- 二、题解
- 方法一:递归(一种麻烦的方法)
- 方法二:优化后的递归
一、题目
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
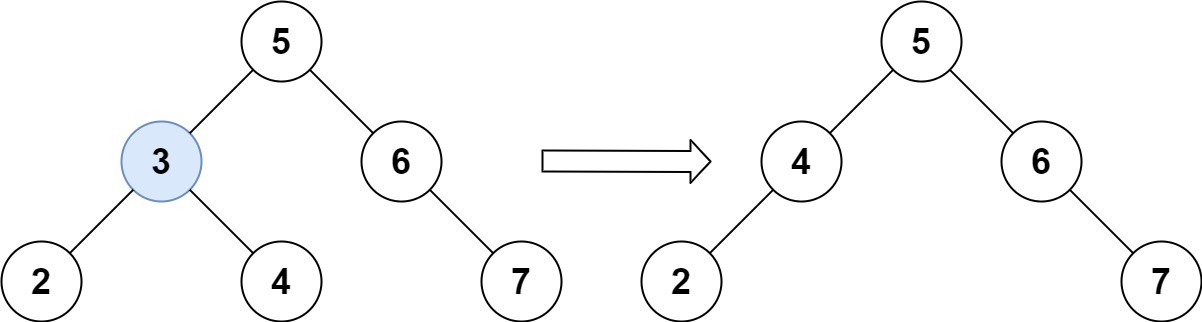
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围
[0, 104]. -105 <= Node.val <= 105- 节点值唯一
root是合法的二叉搜索树-105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
二、题解
方法一:递归(一种麻烦的方法)
主要思路如下:
-
findNode函数:这个函数用于在给定的二叉搜索树中找到值等于target的节点。函数采用递归的方式,在树中搜索目标节点。如果当前节点为空,说明未找到目标节点,返回nullptr。如果当前节点的值等于目标值,返回该节点。如果当前节点的值大于目标值,说明目标节点在左子树中,递归地搜索左子树。否则,目标节点在右子树中,递归地搜索右子树。 -
deleteNode函数:这个函数用于删除二叉搜索树中值为key的节点。首先,通过调用findNode函数找到待删除的节点node,同时维护一个指向node的父节点pre。然后根据删除情况进行不同的处理:- 如果
pre为空,说明待删除节点是根节点。然后根据左右子树的情况进行调整,保留右子树并将左子树插入右子树中的最左叶子节点。 - 如果
pre非空,根据pre的位置判断node是其父节点的左子节点还是右子节点。然后根据左右子树的情况进行调整,同样保留右子树并将左子树插入右子树中的最左叶子节点。
- 如果
最后,删除 node 节点并返回调整后的树。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode *pre = nullptr;TreeNode* findNode(TreeNode *root, int target){if(root == nullptr){return root;}if(root->val == target){return root;}pre = root;if(root->val > target){TreeNode *left = findNode(root->left, target);return left;}else{TreeNode *right = findNode(root->right, target);return right;}}TreeNode* deleteNode(TreeNode* root, int key) {TreeNode *node = findNode(root, key);if(node == nullptr) return root;if(pre == nullptr){if(node->left && node->right){TreeNode *temp = node->right;while(temp->left){temp = temp->left;}temp->left = node->left;return node->right;}else if(node->left){return node->left;}else if(node->right){return node->right;}else{return nullptr;}}if(pre && pre -> right == node){if(node->left && node->right){TreeNode *temp = node->right;while(temp->left){temp = temp->left;}temp->left = node->left;pre->right = node->right;}else if(node->left){pre->right = node->left;}else if(node->right){pre->right = node->right;}else{pre->right = nullptr;}}if(pre && pre->left == node){if(node->left && node->right){TreeNode *temp = node->right;while(temp->left){temp = temp->left;}temp->left = node->left;pre->left = node->right;}else if(node->left){pre->left = node->left;}else if(node->right){pre->left = node->right;}else{pre->left = nullptr;}}delete node;return root;}
};
方法二:优化后的递归
算法思路
-
递归搜索节点: 首先,我们从根节点开始递归地搜索目标节点(值为key的节点)。
- 如果当前节点为空,表示没有找到目标节点,直接返回空指针(nullptr)。
- 如果当前节点的值大于目标key,说明目标节点在左子树中,递归搜索左子树。
- 如果当前节点的值小于目标key,说明目标节点在右子树中,递归搜索右子树。
- 如果当前节点的值等于目标key,说明找到了目标节点,继续下一步。
-
处理删除操作: 一旦我们找到了目标节点,有几种情况需要处理:
- 如果目标节点没有左子树,那么我们可以用其右子树来替代这个节点,然后删除这个节点。
- 如果目标节点没有右子树,类似地,我们可以用其左子树来替代这个节点,然后删除这个节点。
- 如果目标节点既有左子树又有右子树,我们可以找到其右子树中最小的节点(即右子树中的最左节点,即后继节点),将该节点的值复制到目标节点上,然后递归地在右子树中删除这个后继节点。
-
返回根节点: 最后,无论如何都要返回当前子树的根节点。
具体实现
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (!root)return nullptr;if (root->val > key) {root->left = deleteNode(root->left, key); // 递归搜索左子树} else if (root->val < key) {root->right = deleteNode(root->right, key); // 递归搜索右子树} else {if (!root->left) { // 没有左子树,用右子树替代TreeNode* temp = root->right;delete root;return temp;} else if (!root->right) { // 没有右子树,用左子树替代TreeNode* temp = root->left;delete root;return temp;}TreeNode* temp = findMin(root->right); // 找到后继节点root->val = temp->val;root->right = deleteNode(root->right, temp->val); // 在右子树中删除后继节点}return root; // 返回根节点}private:TreeNode* findMin(TreeNode* node) {while (node->left)node = node->left;return node; // 找到最左节点,即后继节点}
};
算法分析
- 在最坏情况下,我们需要遍历BST的高度h,即时间复杂度为O(h)。
- 递归深度取决于树的高度,所以空间复杂度也是O(h)。
相关文章:

LeetCode450. 删除二叉搜索树中的节点
450. 删除二叉搜索树中的节点 文章目录 [450. 删除二叉搜索树中的节点](https://leetcode.cn/problems/delete-node-in-a-bst/)一、题目二、题解方法一:递归(一种麻烦的方法)方法二:优化后的递归 一、题目 给定一个二叉搜索树的根…...

Java动态调试技术原理及实践
文章目录 Java动态调试技术原理及实践引言故事场景一:开发调试动态调试技术简介Java Instrumentation简介动态调试技术实践案例分析场景二:线上问题排查动态调试技术实践案例分析总结Java动态调试技术原理及实践 引言 在日常的软件开发过程中,调试是一个非常重要的环节。当…...

Lua + Redis 实战代码
--[[luarocks install luasocket module socket not foundhttps://github.com/nrk/redis-lua最历害的是,用redis 去跑lua,分布式锁,限流,]]--local redis require("redis");local config{host"127.0.0.1&…...

类的访问限定符,实例化,对象存储方式,this指针
目录 类的定义 类的两种定义方式: 访问限定符 类的实例化 类对象的存储方式 this指针 C语言结构体中只能定义变量,在C中,结构体内不仅可以定义变量,也可以定义函数。比如: 之前在数据结构初阶中,用C语…...

《Linux从练气到飞升》No.15 Linux 环境变量
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux菜鸟刷题集 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的…...

Spring Boot 重启命令
Spring Boot 重启命令 本文描述了一个重启Spring Boot命令执行过程和示例 本文利用kill -9 关闭进程,不优雅,会突然中断程序,可能导致数据和逻辑异常 搜索微信小程序【亚特技术】在资源中搜索【优雅】可得到Spring Boot如何优化重启 1. 过…...
pdf怎么合并在一起?这几个合并方法了解一下
pdf怎么合并在一起?在日常工作、学习和生活中,我们常常会遇到需要将多个PDF文件合并成一个文件的情况。比如,在学术论文写作中,我们可能需要将多篇论文合并成一个文件进行打印和提交。在工作中,我们可能需要将多个报告…...
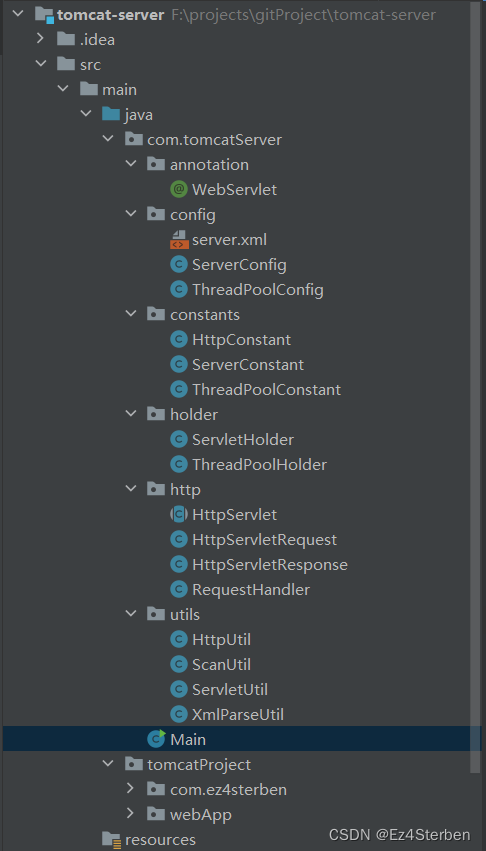
【仿写tomcat】七、项目结构优化以及代码开源
仿写tomcat 项目结构开源地址 项目结构 到目前为止,博主的仿写tomcat就告一段落了,后续有时间了还会继续补充功能,现在的项目结构如下。 在保证功能的前提下作出的改动有: 将各个类中的参数统一成了Config类,通过对…...
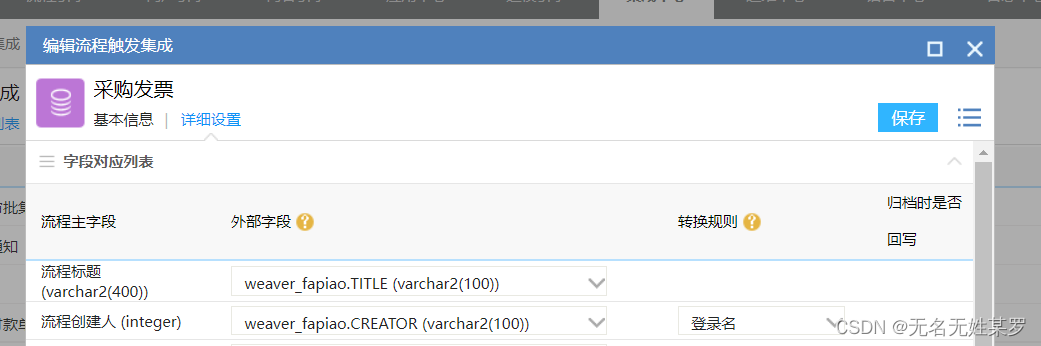
泛微E8配置自定义触发流程失败
在新公司接了个配置泛微流程触发的活。因为泛微的官方文档并没有详细的操作指引,在测试环境配置之后、要触发的流程可以手工提交,但是触发一直不成功。简单记录下业务场景和其他处理信息,以供参考。 应用版本 目前使用了泛微 E8 ࿰…...
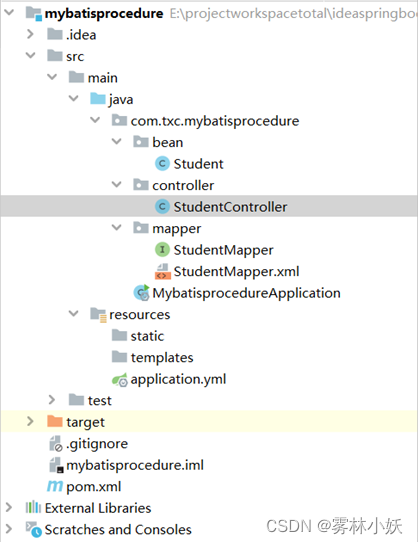
Springboot整合Mybatis调用Oracle存储过程
1、配置说明 Oracel11g+springboot2.7.14+mybatis3.5.13 目标:springboot整合mybatis访问oracle中的存储过程,存储过程返回游标信息。 mybatis调用oracle中的存储过程方式 2、工程结构 3、具体实现 3.1、在Oracle中创建测试数据库表 具体数据可自行添加 create table s…...
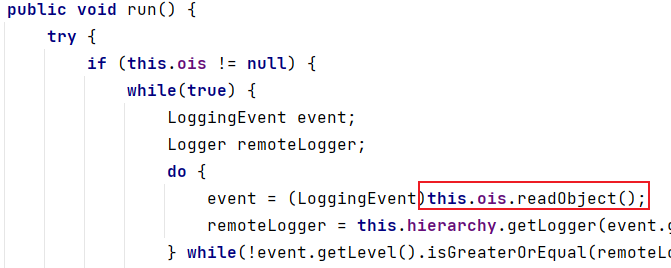
【java安全】Log4j反序列化漏洞
文章目录 【java安全】Log4j反序列化漏洞关于Apache Log4j漏洞成因CVE-2017-5645漏洞版本复现环境漏洞复现漏洞分析 CVE-2019-17571漏洞版本漏洞复现漏洞分析 参考 【java安全】Log4j反序列化漏洞 关于Apache Log4j Log4j是Apache的开源项目,可以实现对System.out…...
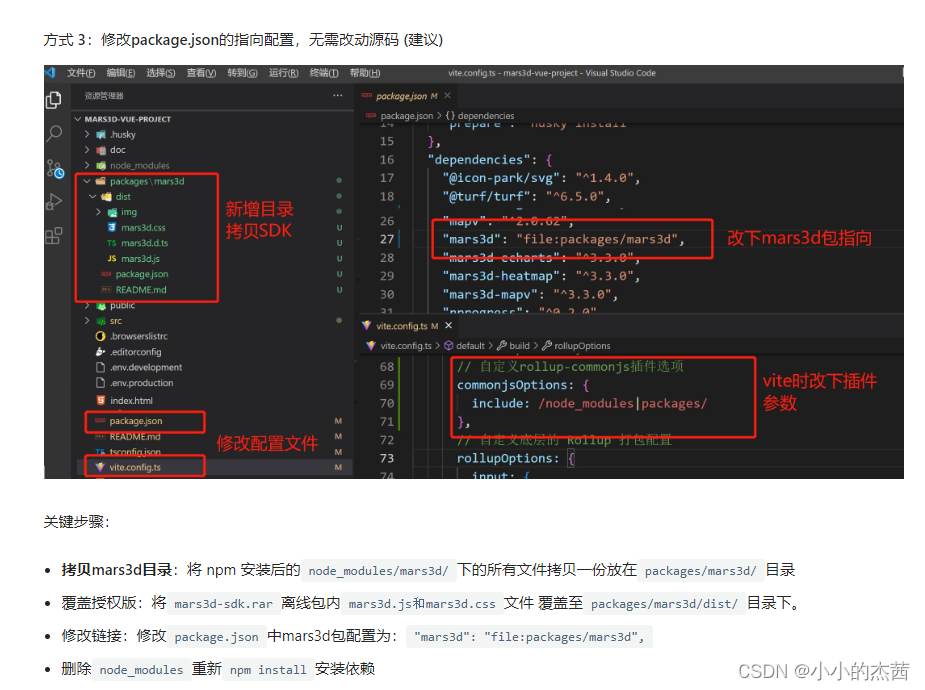
[mars3d 打包]vue3+vite,打包后mars3d找不到
前提 : vue3vite开发框架;使用 官网 方式3获取sdk,引入mars3d; 问题:开发时一切正常,打包之后,页面白屏,没有渲染; 相关的mars3d的相关方法会报错;但是mars3d的打印日志是有的&…...
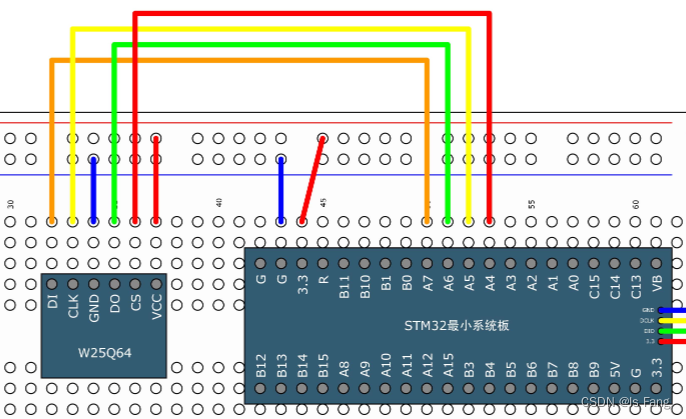
STM32——SPI外设总线
SPI外设简介 STM32内部集成了硬件SPI收发电路,可以由硬件自动执行时钟生成、数据收发等功能,减轻CPU的负担 可配置8位/16位数据帧、高位先行/低位先行 时钟频率: fPCLK / (2, 4, 8, 16, 32, 64, 128, 256) 支持多主机模型、主或从操作 可…...

BOXTRADE-天启量化分析平台 主要功能介绍
BOXTRADE-天启量化分析平台 主要功能介绍 potato 数学 web 缘起 月晕而风,础润而雨 BOXTRADE-天启量化 欢迎来到天启量化!这是一个专注于量化分析的网站。我们致力于为用户提供市场行情技术指标和量化策略分析方面的优质内容和资源。 我们的使命是 做…...
kaggle注册不显示验证码
edge浏览器 1.点击浏览器右上角三个点 2.点击扩展 3.点击管理扩展 4.点击获取Microsoft Edge扩展,在左上角输入Head Editor 5.输入https://www.azurezeng.com/static/HE-GoogleRedirect.json 6.下载后,点保存 成功!...

python爬虫7:实战1
python爬虫7:实战1 前言 python实现网络爬虫非常简单,只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点,方便以后复习。 申明 本系列所涉及的代码仅用于个人研究与讨论,并不会对网站产生不好…...
uniApp引入vant2
uniApp引入vant2 1、cnpm 下载:cnpm i vantlatest-v2 -S2、main.js文件引入 import Vant from ./node_modules/vant/lib/vant;Vue.use(Vant);3.app.vue中引入vant 样式文件 import /node_modules/vant/lib/index.css;...
如何大幅提高遥感影像分辨率(Python+MATLAB)
前言: 算法:NSCT算法(非下采样变换) 数据:Landsat8 OLI 遥感图像数据 编程平台:MATLAB+Python 论文参考:毛克.一种快速的全色和多光谱图像融合算法[J].测绘科学,2016,41(01):151-153+98.DOI:10.16251/j.cnki.1009-2307.2016.01.028. 左图:未进行融合的多光谱真彩色合…...

nginx php-fpm安装配置
nginx php-fpm安装配置 nginx本身不能处理PHP,它只是个web服务器,当接收到请求后,如果是php请求,则发给php解释器处理,并把结果返回给客户端。 nginx一般是把请求发fastcgi管理进程处理,fascgi管理进程选…...

通过ip获取地理位置信息
GeoLite2-City.mmdb 文件是 MaxMind 公司提供的一个免费的 IP 地址与城市地理位置映射数据库文件。它包含了 IP 地址范围与对应的城市、地区、国家、经纬度等地理位置信息的映射。这种数据库文件可以用于识别访问您的应用程序或网站的用户的地理位置,从而实现针对不…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...
