【算法学习】两数之和II - 输入有序数组
题目描述
原题链接
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
提示:
2 <= numbers.length <= 3 * 104-1000 <= numbers[i] <= 1000numbers按 非递减顺序 排列-1000 <= target <= 1000- 仅存在一个有效答案
双指针法
思路分析
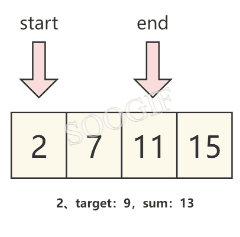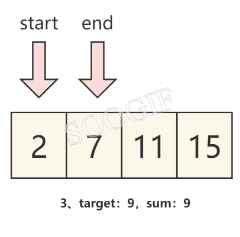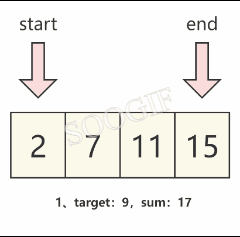
我们观察题目可以发现,数组是已经排好序的,那么我们可以直接定义两个元素来分别指向 数组头 和 数组尾 ,然后循环使两个指针移动,直到最终算出我们需要的结果。
假设左指针为start,右指针为end,并将左右指针所对应的元素的和设为sum,那么我们就可以发现:
- 当 sum==target 时,就可以得到我们需要的结果
- 当 sum>target 时,我们需要将右指针对应的元素变小一些,那么就需要 将右指针向左移动一个元素,也就是
end-- - 当 sum<target 时,我们需要将左指针对应的元素变大一些,那么就需要 将左指针向右移动一个元素,也就是
start++
我们可以通过下图来理解这个规律。
图解
代码实现
public int[] twoSum(int[] numbers, int target) {if (null == numbers) {return new int[0];}int start = 0;int end = numbers.length - 1;while (start < end) {int sum = numbers[start] + numbers[end];if (sum == target) {return new int[]{start + 1, end + 1};} else if (sum > target) {end--;} else {start++;}}return new int[0];
}
二分查找法
思路分析
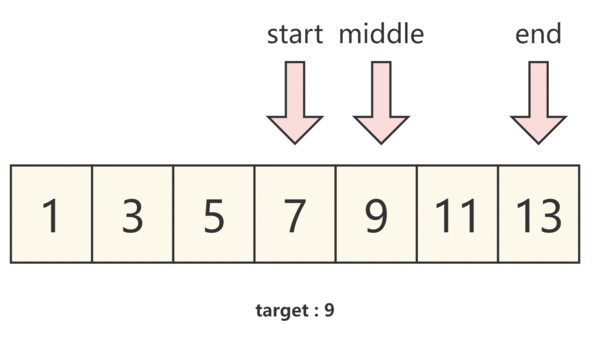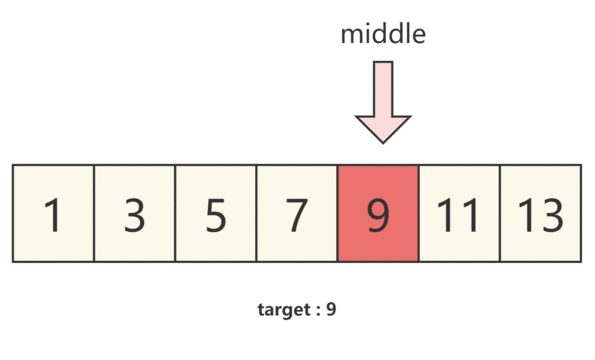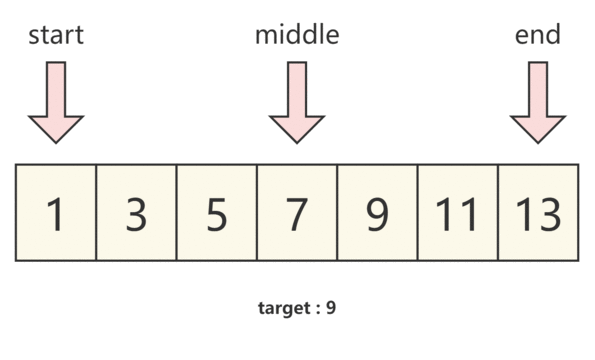
那么我们将题目带入,假设左指针为 start,右指针为 end,并将左右指针中间的下标为 middle,即可得到:
- 当 numbers[middle]==target 时,我们即可得到需要的结果
- 当 numbers[middle]>target 时,说明 中间数大于预期结果,结果在左半部分,那么我们需要 将右指针移动至middle的位置,并重新取middle的位置。
- 当 numbers[middle]<target 时,说明 中间数小于预期结果,结果在右半部分,那么我们需要 将左指针移动至middle的位置,并重新取middle的位置。
我们通过下图来理解。
图解
代码实现
public int[] twoSum(int[] numbers, int target) {if (null == numbers) {return new int[0];}for (int i = 0; i < numbers.length; ++i) {int start = i + 1;int end = numbers.length - 1;while (start <= end) {int middle = (end - start) / 2 + start;if (numbers[middle] == target - numbers[i]) {return new int[]{i + 1, middle + 1};} else if (numbers[middle] > target - numbers[i]) {end = middle - 1;} else {start = middle + 1;}}}return new int[0];}
总结
我们使用了两种写法来完成这个题目:双指针法 和 二分查找法 。
其中在 双指针法 中,数组最多遍历n次,则时间复杂度为 O(n) ,空间复杂度为O(1) 。
在 二分查找法 中,遍历数组的时间复杂度为 O(n) ,二分查找来寻找参数的时间复杂度为 O ( l o g n ) O(log_n) O(logn) ,所以在该题目中,总时间复杂度为 O ( n l o g n ) O(nlog_n) O(nlogn) ,空间复杂度为O(1) 。
推荐
关注博客和公众号获取最新文章
Bummon’s Blog | Bummon’s Home | 公众号
相关文章:

【算法学习】两数之和II - 输入有序数组
题目描述 原题链接 给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 < index1 < …...

聚观早报|京东称在技术投入没有止境;木蚁机器人完成B2轮融资
【聚观365】8月18日消息 京东零售CEO表示在技术上投入没有止境 木蚁机器人完成B2轮超亿元融资 耐能推出AI芯片KL730 三星电子泰勒晶圆厂首家客户是AI半导体厂商 韩国新能源汽车7月出口额同比大增36% 京东零售CEO表示在技术上投入没有止境 近日,京东零售CEO辛利…...
C语言:选择+编程(每日一练)
目录 选择题: 题一: 题二: 题三: 题四: 题五: 编程题: 题一:尼科彻斯定理 示例1 题二:等差数列 示例2 本人实力有限可能对一些地方解释和理解的不够清晰&…...

信道数据传输速率、码元传输速率、调制速度,信号传播速度之间的关系
1、信道数据传输速率(bit/s) 举例:移动通信中的数据传输速率。假设你的手机连接到4G网络,该网络的最大理论数据传输速率为100 Mbps。这意味着在理想情况下,你的手机可以以每秒100兆比特的速度传输数据。 2、码元传输速…...

docker的使用方法总结
Docker是一个非常强大的工具,它可以用于创建、部署和运行应用程序。以下是一些docker相关的常用指令, 1、查看docker版本 docker version 2、查看正在运行的Docker容器 docker ps 3、查看所有的docker容器(包括没有运行的容器࿰…...
【C#】条码管理操作手册
前言:本文档为条码管理系统操作指南,介绍功能使用、参数配置、资源链接,以及异常的解决等。思维导图如下: 一、思维导图 二、功能操作–条码打印(客户端) 2.1 参数设置 功能介绍:二维码图片样…...
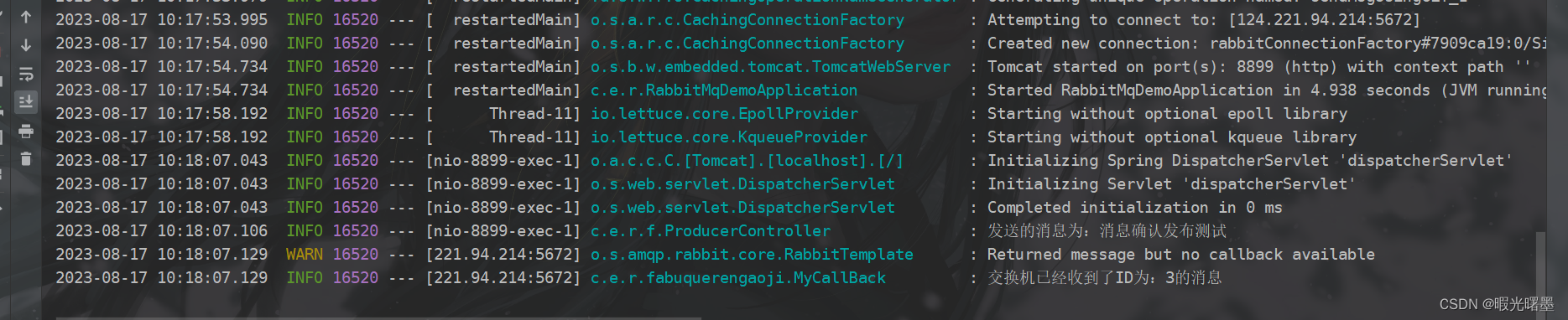
RabbitMq-发布确认高级(避坑指南版)
在初学rabbitMq的时候,伙伴们肯定已经接触到了“发布确认”的概念,但是到了后期学习中,会接触到“springboot”中使用“发布确认”高级的概念。后者主要是解决什么问题呢?或者是什么样的场景引出这样的概念呢? 在生产环…...

Blender增强现实3D模型制作指南【AR】
推荐:用 NSDT编辑器 快速搭建可编程3D场景 将静态和动画 3D 内容集成到移动增强现实 (AR) 体验中是增强用户沉浸感和参与度的高效方法。 然而,为 AR 创建 3D 对象可能相当艰巨,尤其是对于那些缺乏 3D 建模经验的人来说。 与添加视频或照片 AR…...
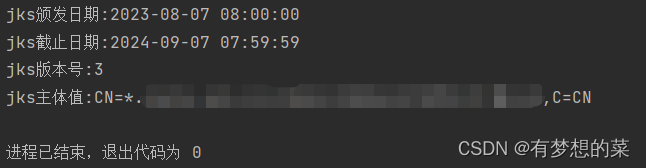
Java查看https证书过期时间(JKS,CERT)
在这里需要使用X.509 证书的抽象类 X509Certificate 。此类提供了一种访问 X.509 证书所有属性的标准方式。 这些证书被广泛使用以支持 Internet 安全系统中的身份验证和其他功能。常见的应用包括增强保密邮件 (PEM)、传输层安全 (SSL)、用于受信任软件发布的代码签名和安全电…...
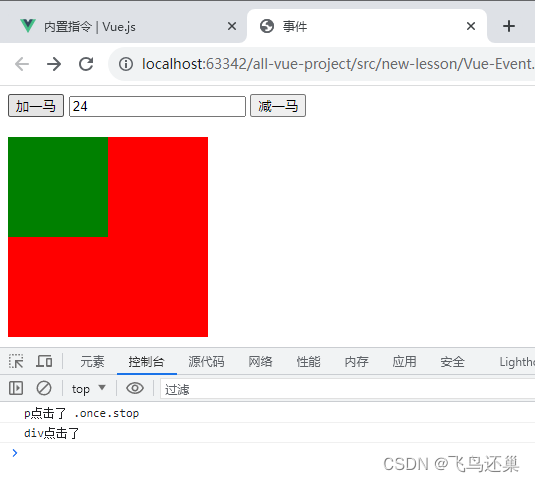
关于vue,记录一次修饰符.stop和.once的使用,以及猜想。
内置指令 | Vue.js 在vue的api里,关于v-on有stop和once两个事件标签。 .stop - 调用 event.stopPropagation()。.once - 最多触发一次处理函数。 原有主要代码和页面效果 (无stop和once): ...<div class"div" click"di…...
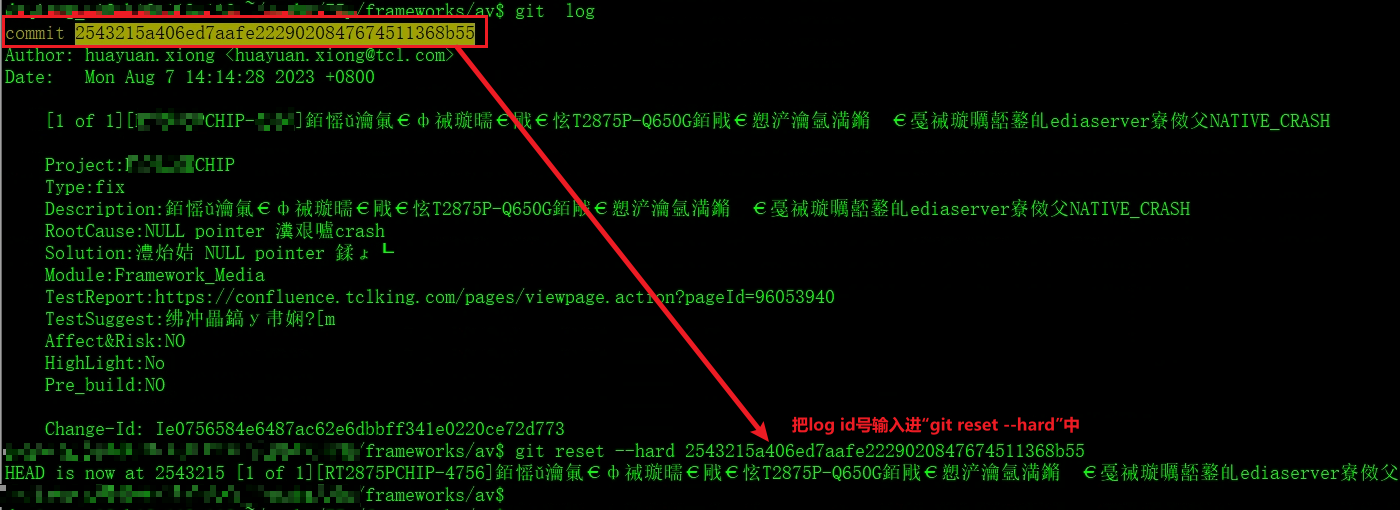
解决git reset --soft HEAD^撤销commit时报错
今天在使用git回退功能的时候,遇到以下错误: 解决git reset --soft HEAD^撤销commit时报错 问题: 在进行完commit后,想要撤销该commit,于是使用了git reset --soft HEAD^命令,但是出现如下报错࿱…...
)
【BASH】回顾与知识点梳理(三十四)
【BASH】回顾与知识点梳理 三十四 三十四. 认识系统服务(二)34.1 systemctl 针对 service 类型的配置文件systemctl 配置文件相关目录简介systemctl 配置文件的设定项目简介[Unit] 部份[Service] 部份[Install] 部份 两个 vsftpd 运作的实例多重的重复设…...

Python可视化在量化交易中的应用(11)_Seaborn折线图
举个栗子,用seaborn绘制折线图。 Seaborn中折线图的绘制方法 在seaborn中,我们一般使用sns作为seaborn模块的别名,因此,在下文中,均以sns指代seaborn模块。 seaborn中绘制折线图使用的是sns.plot()函数: …...

无涯教程-TensorFlow - TensorBoard可视化
TensorFlow包含一个可视化工具,称为TensorBoard,它用于分析数据流图,还用于了解机器学习模型。 TensorBoard的重要功能包括查看有关垂直对齐的任何图形的参数和详细信息的不同类型统计的视图。 深度神经网络包括多达36,000个节点…...

[uni-app] uview封装Popup组件,处理props及v-model的传值问题
文章目录 需求及效果遇到的问题解决的办法偷懒的写法 需求及效果 uView(1.x版本)中, 有Pop弹出层的组件, 现在有个需求是,进行简单封装,有些通用的设置不想每次都写(比如 :mask-custom-style"{background: rgba(0, 0, 0, 0.7)}"这种) 然后内部内容交给插槽去自己随…...

【C++】int a;和int *p=new int;有什么区别?
2023年8月19日,周六早上 int a; 和 int *p new int; 之间有以下区别: 1. 内存分配方式:int a; 是在栈上分配内存,而 int *p new int; 是在堆上动态分配内存。 2. 生命周期:int a; 的生命周期与其所在的作用域相同&…...
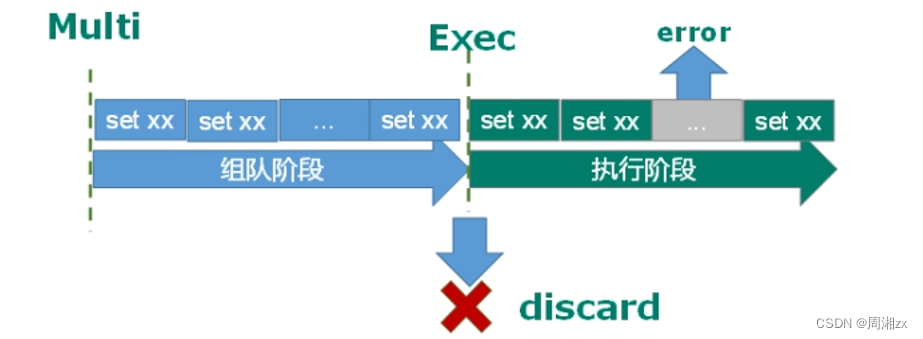
redis事务管理
目录 一、redis事务定义 二、事务控制命令——Multi、Exec、discard 三、事务的错误处理 四、事务的冲突问题 悲观锁 乐观锁 WATCH unwatch 五、事务特性 单独的隔离操作 没有隔离级别的概念 不保证原子性 一、redis事务定义 Redis 事务是一个单独的隔离操作&…...
TPS_C++版本及功能支持备注
TPS_C版本及功能支持备注 相关参考链接C23:https://zh.cppreference.com/w/cpp/23 相关参考链接C20:https://zh.cppreference.com/w/cpp/20 相关参考链接C17:https://zh.cppreference.com/w/cpp/17 相关参考链接C14:https://zh.cp…...
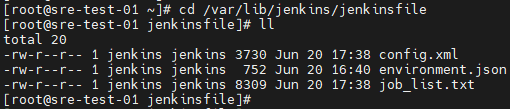
同步jenkinsfile流水线(sync-job)
环境 变量:env(环境变量:sit/dev/simulation/prod/all),job(job-name/all)目录:/var/lib/jenkins/jenkinsfile environment.json: [roottest-01 jenkinsfile]# cat env…...

STM32单片机WIFI-APP智能温室大棚系统CO2土壤湿度空气温湿度补光
实践制作DIY- GC0161--智能温室大棚系统 基于STM32单片机设计---智能温室大棚系统 二、功能介绍: 电路组成:STM32F103CXT6最小系统LCD1602显示器DHT11空气温度湿度光敏电阻光强土壤湿度传感器SGP30二氧化碳传感器 1个继电器(空气加湿&#x…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
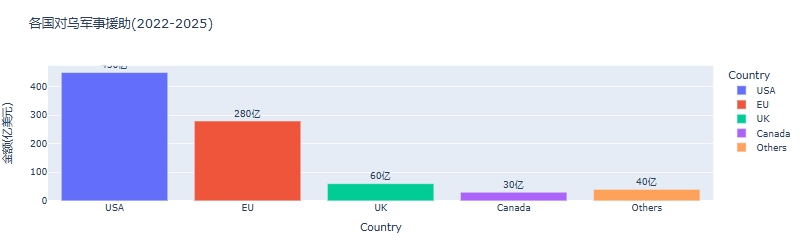
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...
