NOIP 2006 普及组 第二题 开心的金明
开心的金明
说明
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。 更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过N元钱就行”。 今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的N元。
于是,他把每件物品规定了一个重要度,分为5等:用整数1~5 表示,第5等最重要。 他还从因特网上查到了每件物品的价格(都是整数元)。 他希望在不超过N元(可以等于N元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第j件物品的价格为v[j],重要度为w[j],共选中了k件物品,编号依次为j1,j2,……,jk,则所求的总和为:v[j1]*w[j1]+v[j2]*w[j2]+…+v[jk]*w[jk] 。(其中*为乘号)
请你帮助金明设计一个满足要求的购物单。
输入格式
输入的第1行,为两个正整数,用一个空格隔开:N m(其中N(<30000)表示总钱数,m(<25)为希望购买物品的个数。)
从第2行到第m+1行,第j行给出了编号为j−1的物品的基本数据,每行有2个非负整数v p(其中v表示该物品的价格(v<=10000),p表示该物品的重要度(1~5))
输出格式
输出只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(<100000000)。
样例
提示
NOIP 2006 普及组 第二题
#include<bits/stdc++.h>
using namespace std;
int q,w,e,r,t,y,u,o,p,s,d,f,g,h,j,l,z,x,c,v,n,m,i,k,a[100],aa[100],aaa[100],b[100][30010],bb[100][100];
int main()
{cin>>m>>n;for(i=1;i<=n;i++){cin>>a[i]>>aa[i];}for(i=1;i<=n;i++){for(j=0;j<=m;j++){b[i][j]=b[i-1][j];if(j>=a[i])b[i][j]=max(b[i][j],b[i-1][j-a[i]]+a[i]*aa[i]);}}for(i=0;i<=m;i++){p=max(p,b[n][i]);}cout<<p;return 0;
}
相关文章:

NOIP 2006 普及组 第二题 开心的金明
开心的金明 说明 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。 更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超…...

「UG/NX」Block UI 指定点SpecifyPoint
✨博客主页何曾参静谧的博客📌文章专栏「UG/NX」BlockUI集合📚全部专栏「UG/NX」NX二次开发「UG/NX」BlockUI集合「VS」Visual Studio「QT」QT5程序设计「C/C+&#...

Linux Shell如果ping失败就重启网卡(详解)
直接上脚本 -------------------------------------------------------------------------- #vi /tmp/ping_check.sh #!/bin/bash IP="1.1.1.1" PacketLoss=`ping -c 4 -w 4 1.1.1.1 | grep packet loss | awk -F packet loss {print $1} | awk {print $NF}|se…...
每天一道leetcode:剑指 Offer 13. 机器人的运动范围(中等广度优先遍历剪枝)
今日份题目: 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0]的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之…...

TypeError: a bytes-like object is required, not ‘str‘
raceback (most recent call last): File "D:\pycharmcode\client.py", line 12, in <module> tcp_socket.send(send_data) TypeError: a bytes-like object is required, not str 使用socket进行ubuntu与windows通信时,发送数据时报了以上错…...

题解 | #1005.List Reshape# 2023杭电暑期多校9
1005.List Reshape 签到题 题目大意 按一定格式给定一个纯数字一维数组,按给定格式输出成二维数组。 解题思路 读入初始数组字符串,将每个数字分离,按要求输出即可 参考代码 参考代码为已AC代码主干,其中部分功能需读者自行…...
会声会影2023旗舰版电脑端视频剪辑软件
随着短视频、vlog等媒体形式的兴起,视频剪辑已经成为了热门技能。甚至有人说,不会修图可以,但不能不会剪视频。实际上,随着各种智能软件的发展,视频剪辑已经变得越来越简单。功能最全的2023新版,全新视差转…...

【linux基础(四)】对Linux权限的理解
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到开通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux权限 1. 前言2. shell命…...

maven项目指定数据源
springboot项目 直接在pom.xml文件中添加以下配置 <!--使用阿里云maven中央仓库--> <repositories><repository><id>aliyun-repos</id><url>http://maven.aliyun.com/nexus/content/groups/public/</url><snapshots><ena…...

web3:使用Docker-compose方式部署blockscout
最近做的项目,需要blockscout来部署一个区块链浏览器,至于blockscout是什么,咱们稍后出一篇文章专门介绍下,本次就先介绍一下如何使用Docker-compose方式部署blockscout,以及过程中遇到的种种坑 目录 先决条件我的环境准备工作Docker-compose1.安装方式一:下载 Docker Co…...
泛型编程加载dll接口函数)
C++11实用技术(五)泛型编程加载dll接口函数
C11泛型编程简化加载dll代码 常见的加载dll方式: HMODULE m_hDataModule; m_hDataModule LoadLibrary("myDll.dll");typedef int (*PfunA)(int a, int b);//定义函数指针 PfunA fun (PfunA)(GetProcAddress(m_hDataModule , "funA"));//加载…...
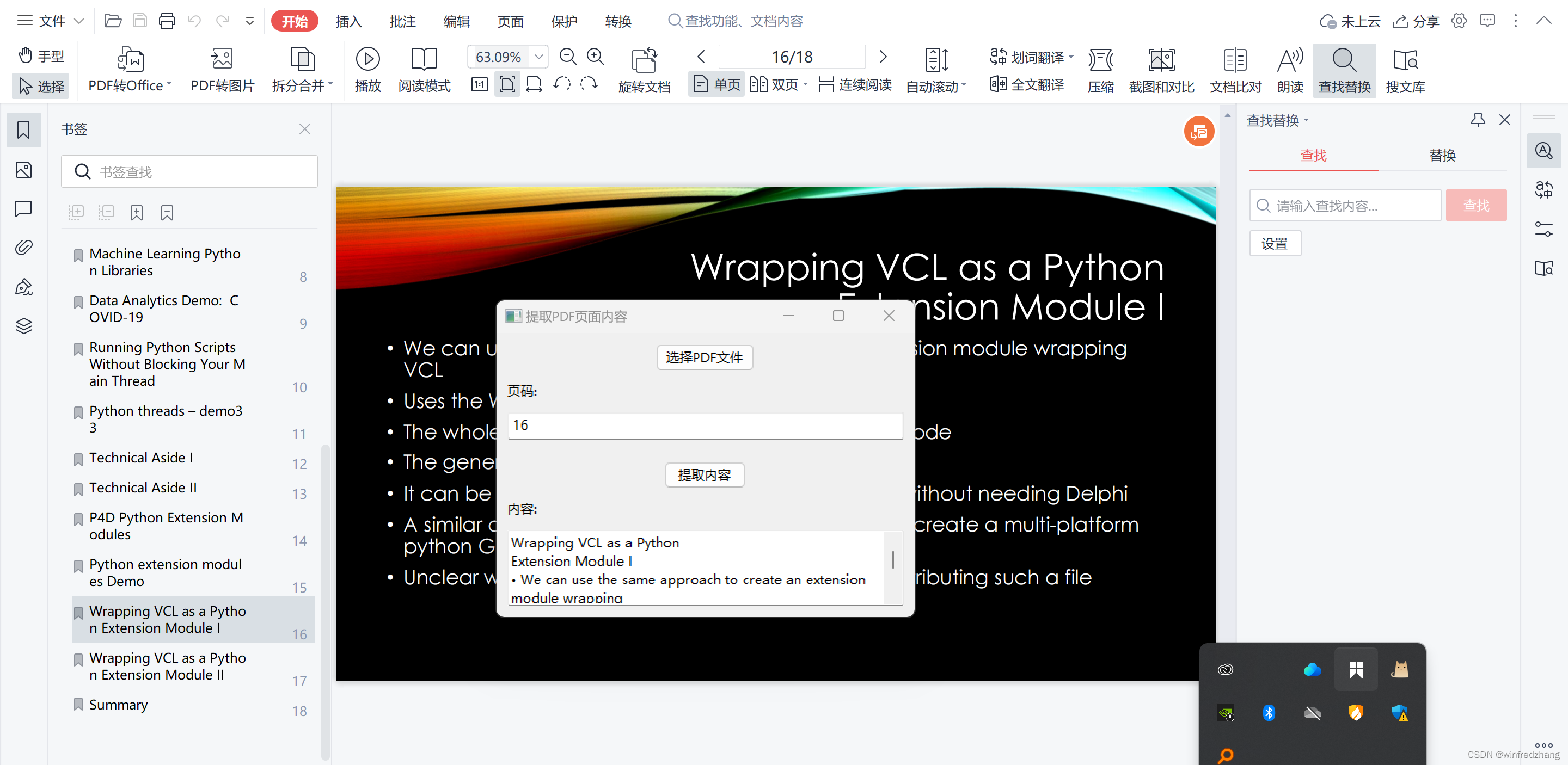
使用wxPython和PyMuPDF提取PDF页面指定页数的内容的应用程序
在本篇博客中,我们将探讨如何使用wxPython和PyMuPDF库创建一个简单的Bokeh应用程序,用于选择PDF文件并提取指定页面的内容,并将提取的内容显示在文本框中。 C:\pythoncode\new\pdfgetcontent.py 准备工作 首先,确保你已经安装了…...

k8s的pv和pvc创建
//NFS使用PV和PVC 1、配置nfs存储 2、定义PV 实现 下图的pv和pvc测试 pv的定义 这里定义5个PV,并且定义挂载的路径以及访问模式,还有PV划分的大小 vim /pv.yamlapiVersion: v1 kind: PersistentVolume metadata:name: pv001 spec:capacity:storage: …...

记K8S集群工作节点,AnolisOS 8.6部署显卡驱动集成Containerd运行时
1、安装gcc #安装编译环境 yum -y install make gcc gcc-c2、下载显卡驱动 点击 直达连接 nvidia高级搜索下载历史版本驱动程序(下载历史版本驱动) https://www.nvidia.cn/Download/Find.aspx?langcn3、安装驱动 安装显卡驱动 ./NVIDIA-Linux-x86…...

JavaScript 性能优化
优化JavaScript代码的性能是开发过程中的一个关键任务,它可以显著提升网站或应用的用户体验。以下是一些优化技巧,涵盖了减少重绘、减少内存占用和合并网络请求等方面: 1. **减少重绘和重排:** - **使用 CSS3 动画:…...
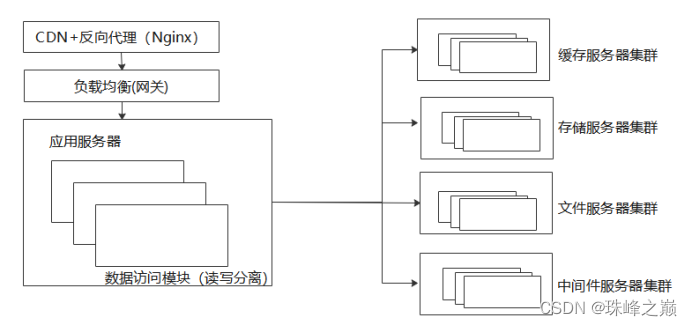
架构演进及常用架构
1架构演进及常用架构 1.1单体分层架构 1.2 多应用微服务架构 1.3 分布式集群部署 部署 CDN 节点: 用户访问量的增加意味着用户地域的分散请求,如果所有请求都直接发送中心服务器的话,距离越远,响应速度越差,这时就需…...

WinCC V7.5 中的C脚本对话框不可见,将编辑窗口移动到可见区域的具体方法
WinCC V7.5 中的C脚本对话框不可见,将编辑窗口移动到可见区域的具体方法 由于 Windows 系统更新或使用不同的显示器,在配置C动作时,有可能会出现C脚本编辑窗口被移动到不可见区域的现象。 由于该窗口无法被关闭,故无法进行进一步…...
【实战】十一、看板页面及任务组页面开发(二) —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(二十四)
文章目录 一、项目起航:项目初始化与配置二、React 与 Hook 应用:实现项目列表三、TS 应用:JS神助攻 - 强类型四、JWT、用户认证与异步请求五、CSS 其实很简单 - 用 CSS-in-JS 添加样式六、用户体验优化 - 加载中和错误状态处理七、Hook&…...

Vue2.7.14、vuecli@5.0.8 升级 vite@4.4.8
项目背景 Vue2.7.14、vuecli5.0.8、element-ui2.15.13、node14.18.3 vite安装 pnpm add vite4.4.8 -D 入口文件index.html 文件位置修改 将pulic里的index.html移到根目录下 根目录/public/index.html 到 根目录/index.html 文件内容修改 <link rel"icon"…...
LeetCode[面试题04.12]求和路径
难度:Medium 题目: 给定一棵二叉树,其中每个节点都含有一个整数数值(该值或正或负)。设计一个算法,打印节点数值总和等于某个给定值的所有路径的数量。注意,路径不一定非得从二叉树的根节点或叶节点开始或结束&#x…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
