第三章 图论 No.13拓扑排序
文章目录
- 裸题:1191. 家谱树
- 差分约束+拓扑排序:1192. 奖金
- 集合+拓扑序:164. 可达性统计
- 差分约束+拓扑序:456. 车站分级
拓扑序和DAG有向无环图联系在一起,通常用于最短/长路的线性求解

裸题:1191. 家谱树
1191. 家谱树 - AcWing题库
#include <iostream>
#include <cstring>
using namespace std;const int N = 110, M = 10010;
int h[N], e[M], ne[M], idx;
int d[N], q[N], hh, tt = -1;
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void topsort()
{for (int i = 1; i <= n; ++ i )if (!d[i]) q[ ++ tt ] = i;while (tt >= hh ){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (-- d[y] == 0) q[++ tt] = y;}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d", &n);for (int x = 1; x <= n; ++ x ){int y;while (scanf("%d", &y), y){add(x, y);d[y] ++ ;}}topsort();for (int i = 0; i <= tt; ++ i )printf("%d ", q[i]);return 0;
}
差分约束+拓扑排序:1192. 奖金
1192. 奖金 - AcWing题库
由于图中所有边权都是正数,可以直接使用topsort求解差分约束问题
根据题意,要求一个最小值,使用最长路求解,转化题目的条件: A > = B + 1 A >= B + 1 A>=B+1与 x i > = x 0 + 100 x_i >= x_0 + 100 xi>=x0+100
x 0 x_0 x0为一个虚拟源点,向每个点连了一条权值为100的边
若图中存在环,topsort的队列长度将小于n,因为环的起点无法进入队列
先用topsort判断图中是否存在环,若不存在,根据拓扑序遍历图,求解最长路
#include <iostream>
#include <cstring>
using namespace std;const int N = 10010, M = 30010;
int h[N], e[M], ne[M], w[M], idx;
int q[N], d[N], hh, tt = -1;
int dis[N];
int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}bool topsort()
{q[ ++ tt ] = 0;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i] ){int y = e[i];if ( -- d[y] == 0) q[ ++ tt ] = y;}}return tt == n;
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i ){int x, y;scanf("%d%d", &x, &y);add(y, x, 1);d[x] ++ ;}for (int i = 1; i <= n; ++ i ) add(0, i, 100), d[i] ++ ;if (!topsort()) puts("Poor Xed");else {for (int k = 0; k <= tt; ++ k ){int x = q[k];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];dis[y] = max(dis[y], dis[x] + w[i]);}}int sum = 0;for (int i = 1; i <= n; ++ i ) sum += dis[i];printf("%d\n", sum);}return 0;
}
debug:最后的遍历没有按照拓扑序
for (int x = 0; x <= tt; ++ x )
{for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];dis[y] = max(dis[y], dis[x] + w[i]);}
}
集合+拓扑序:164. 可达性统计
[164. 可达性统计 - AcWing题库](https://www.acwing.com/problem/content/description/166/
从集合的角度思考, f ( i ) f(i) f(i)表示i这个点能到达的所有点,i首先能到达自己,其次能达到 f ( j 1 ) , f ( j 2 ) , . . . , f ( j n ) f(j_1), f(j_2), ... , f(j_n) f(j1),f(j2),...,f(jn),假设i与n个点直接相连
那么要求 f ( i ) f(i) f(i),就必须求出 f ( j 1 ) , f ( j 2 ) , . . . , f ( j n ) f(j_1), f(j_2), ... , f(j_n) f(j1),f(j2),...,f(jn),即拓扑排序中位于i之后的所有点的 f ( j ) f(j) f(j)
所以这题先拓扑排序,再根据拓扑排序的逆序,求 f ( i ) f(i) f(i)
如何表示集合 f ( i ) f(i) f(i)?用STL的容器bitset,假设图中有N个点,那么bitset的长度为N,每个点都用一个bitset记录其集合,1表示i能递达这个点,0表示不能递达
那么 f ( i ) = f ( j 1 ) ∩ f ( j 2 ) ∩ . . . ∩ f ( j n ) f(i) = f(j_1)∩ f(j_2)∩ ...∩f(j_n) f(i)=f(j1)∩f(j2)∩...∩f(jn)
关于bitset的使用,bitset之间支持|=运算,count()输出bitset中1的个数
#include <iostream>
#include <cstring>
#include <bitset>
using namespace std;const int N = 30010, M = N;
int h[N], e[M], ne[M], idx;
int q[N], d[N], hh, tt = -1;
bitset<N> f[N];
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void topsort()
{for (int i = 1; i <= n; ++ i )if (!d[i]) q[ ++ tt ] = i;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if ( -- d[y] == 0) q[ ++ tt ] = y;}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 0; i < m; ++ i ){int x, y;scanf("%d%d", &x, &y);add(x, y);d[y] ++ ;}topsort();for (int i = tt; i >= 0; -- i ){int x = q[i];f[x][x] = 1;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];f[x] |= f[y];}}for (int i = 1; i <= n; ++ i ) printf("%d\n", f[i].count());return 0;
}
差分约束+拓扑序:456. 车站分级
456. 车站分级 - AcWing题库
分析题意:对于每一条路线,未经过的站点的等级一定小于经过的站点等级,并且最低的站点等级为1级
题目要求所有等级划分中的最少等级数,用最长路求最小值。将以上条件转换成差分约束中的两个条件: B > = A + 1 B >= A + 1 B>=A+1, x i > = x 0 + 1 x_i >= x_0 + 1 xi>=x0+1
x 0 x_0 x0为虚拟源点,通过 x 0 x_0 x0能到达图中的所有点,那么就一定能递达所有边
由于每条路线路都会建立n * m条边,极端情况下可能会爆空间,所以考虑如何优化
一条路径中未经过的站点将向经过的站点连接一条权值为1的边,一共n * m条,由于这些边的权值相同,可以在这些边中创建一个虚拟点v,未经过的点分别向v连一条权值为0的边,v向经过的点分别连接一条权值为1的边。这样,从未经过的点到经过的点的权值和依然为1,但是需要建立的边数为n + m,此时的边数在极端情况下也不会爆空间
#include <iostream>
#include <cstring>
using namespace std;const int N = 2010, M = 1e6 + 10;
int h[N], e[M], ne[M], w[M], idx;
int d[N], q[N], hh, tt = -1;
bool st[N]; int dis[N];
int n, m;void add(int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void topsort()
{for (int i = 1; i <= n + m; ++ i ) if (!d[i]) q[ ++ tt ] = i;while (tt >= hh){int x = q[hh ++ ];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (-- d[y] == 0) q[ ++ tt ] = y;}}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);for (int i = 1; i <= m; ++ i ){memset(st, false, sizeof(st));int t, start = n, end = 0;scanf("%d", &t);while (t -- ){int x;scanf("%d", &x);st[x] = true;start = min(start, x), end = max(end, x);}int v = n + i;for (int i = start; i <= end; ++ i ){if (st[i]) add(v, i, 1), d[i] ++ ;else add(i, v, 0), d[v] ++ ;}}topsort();for (int i = 1; i <= n; ++ i ) dis[i] = 1;for (int i = 1; i <= tt; ++ i ){int x = q[i];for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];dis[y] = max(dis[y], dis[x] + w[i]);}}int res = 0;for (int i = 1; i <= n; ++ i ) res = max(res, dis[i]);printf("%d\n", res);return 0;
}
debug:w[M]写成了w[N],又是这样,然后debug了半天,了
相关文章:

第三章 图论 No.13拓扑排序
文章目录 裸题:1191. 家谱树差分约束拓扑排序:1192. 奖金集合拓扑序:164. 可达性统计差分约束拓扑序:456. 车站分级 拓扑序和DAG有向无环图联系在一起,通常用于最短/长路的线性求解 裸题:1191. 家谱树 119…...

喜报 | 擎创再度入围IDC中国FinTech 50榜单
8月16日,2023年度“IDC中国FinTech 50”榜单正式揭晓,擎创科技继2022年入选该榜单后,再次以创新者姿态成功入选,并以技术赋能业务创新,成为中国金融科技领域创新与活力的重要贡献者。 “IDC中国FinTech 50”旨在评选出…...

【C++ 记忆站】引用
文章目录 一、引用概念二、引用特性1、引用在定义时必须初始化2、一个变量可以有多个引用3、引用一旦引用一个实体,再不能引用其他实体 三、常引用四、使用场景1、做参数1、输出型参数2、大对象传参 2、做返回值1、传值返回2、传引用返回 五、传值、传引用效率比较六…...

Hlang--用Python写个编程语言-变量的实现
文章目录 前言语法规则表示次幂实现变量实现优先级实现步骤解析关键字语法解析解释器总结前言 先前的话,我们终于是把我们整个架子搭起来了,这里重复一下我们的流程,那就是,首先,我们通过解析文本,然后呢遍历文本当中的我们定义的合法关键字,然后呢,把他们封装为一个T…...

多维时序 | MATLAB实现PSO-CNN-BiLSTM多变量时间序列预测
多维时序 | MATLAB实现PSO-CNN-BiLSTM多变量时间序列预测 目录 多维时序 | MATLAB实现PSO-CNN-BiLSTM多变量时间序列预测基本介绍模型特点程序设计参考资料 基本介绍 本次运行测试环境MATLAB2021b,MATLAB实现PSO-CNN-BiLSTM多变量时间序列预测。代码说明:…...

实现Java异步调用的高效方法
文章目录 为什么需要异步调用?Java中的异步编程方式1. 使用多线程2. 使用Java异步框架 异步调用的关键细节结论 🎉欢迎来到Java学习路线专栏~实现Java异步调用的高效方法 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博…...
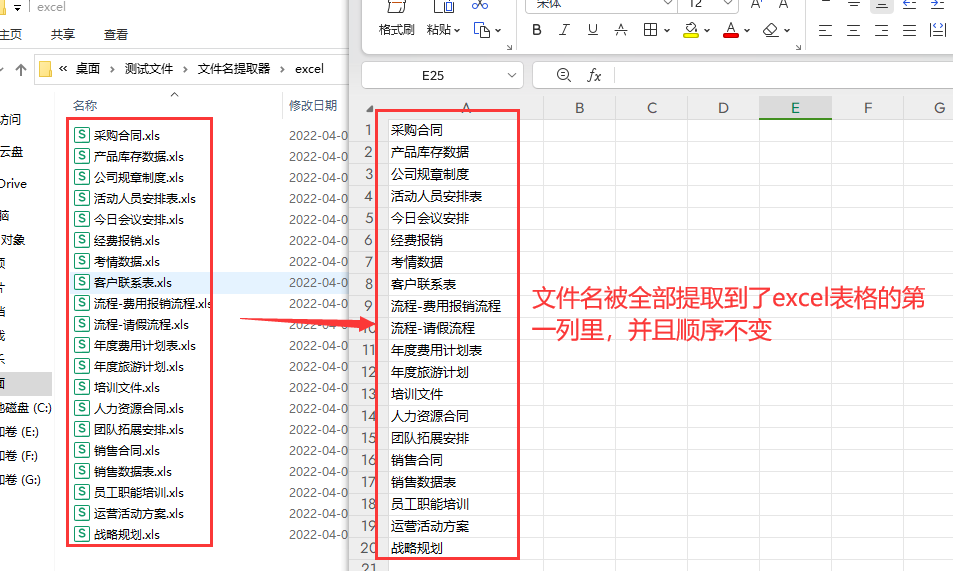
批量提取文件名到excel,详细的提取步骤
如何批量提取文件名到excel?我们的电脑中可能存储着数量非常多的电子文件,现在需要快速将这些文件的名称全部提取到Excel中。虽然少量数据可以通过复制粘贴的方式轻松完成,但是对于上万个数据而言,复制粘贴都是行不通的࿰…...

C#中的泛型约束可以用在以下几个地方?
1.泛型类型参数: 在定义泛型类型或泛型方法时,可以使用泛型约束来限制泛型类型参数的类型。这可以确保类型参数满足特定的条件,从而在编译时捕获错误并提供更安全和可靠的代码。 public class MyClass<T> where T : IComparable<T&…...
Linux Vm上部署Docker
创建ubutu虚拟机并远程连接, 参考 https://blog.csdn.net/m0_48468018/article/details/132267096 在终端中切换到root用户,并安装docker服务 2.1 切换到root用户 sudo su2.2 安装docker服务 , 参考 https://docs.docker.com/engine/install/ubuntu/ …...

ubuntu bind dns服务配置
sudo apt-get install bind9 内网搭建DNS服务器,大多数是解析纯内网地址使用。但是偶尔也需要解析外网的地址,所以我们可以配置DNS没有添加A记录的URL时,forward到外网DNS服务器或者内网的其他DNS服务器解析。 打开配置文件: sud…...

安卓的代码加固和其他安全问题
文章目录 安卓加固apk文件结构dex加固过程 其它安全问题 安卓加固 从App的加固技术来看:主流分为dex加密和so加密,目前来看保护dex文件更为重要,因为dex反编译后的java代码可读性更强。 android-ndk: Native Development Kit 官网解释:这套工具使您能在 Android 应…...
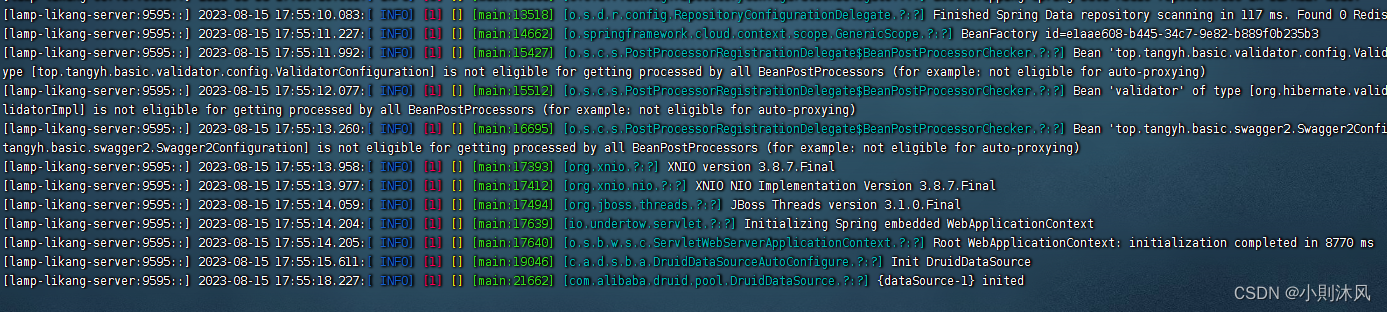
关于Linux Docker springboot jar 日志时间不正确 问题解决
使用Springboot项目的jar,制作了一个Docker镜像,启动该镜像后发现容器和容器中的Springboot 项目的日志时间不正确。 解决 查看容器时间命令为: docker exec 容器id date 1. 容器与宿主机同步时间 在启动镜像时候把操作系统的时间通过&q…...

提高批量爬虫工作效率
大家好!作为一名专业的爬虫程序员,我今天要和大家分享一些关于提高批量爬虫工作效率的实用技巧。无论你是要批量采集图片、文本还是视频数据,这些经验都能帮助你在大规模数据采集中事半功倍。废话不多说,让我们开始吧!…...
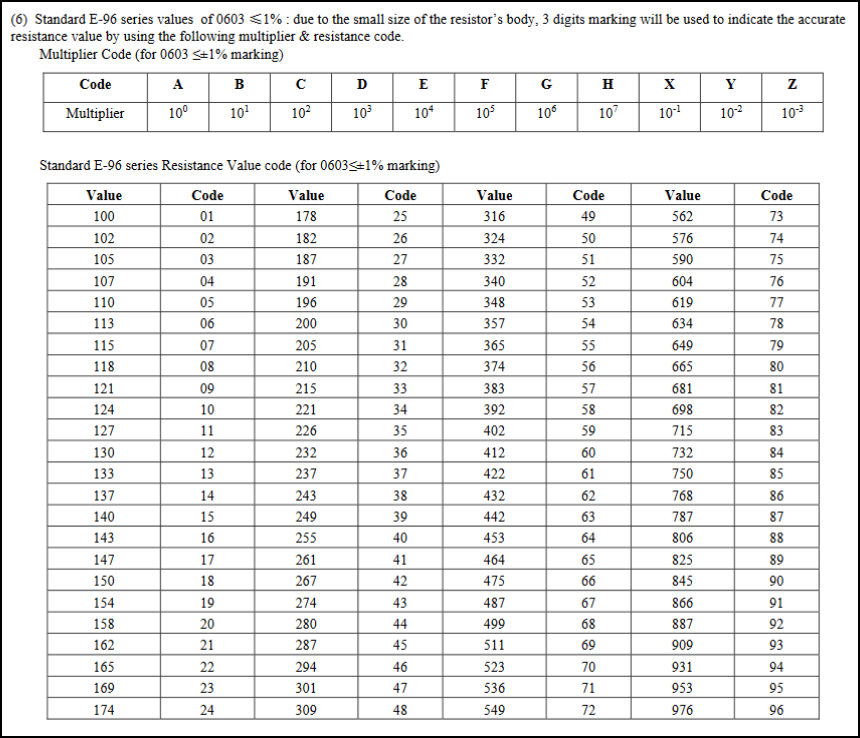
E96系列电阻阻值和代码、乘数对照表
1、为什么要用代码表示? 0805封装还可以简单易懂写下四位丝印,比如10K的1002,但0603的封装上面再想写下四位丝印就没空间了,就算写了也不容易看不清。 2、E96系列电阻阻值和代码、乘数对照表 下面是E96系列的对照表,…...

基于CentOS7.9安装部署docker(简洁版)
安装部署 1基于官方脚本安装(不推荐 不能自行选择版本) 官方文档:https://docs.docker.com/engine/install/centos/ 2 使用yum安装 阿里云文档:docker-ce镜像_docker-ce下载地址_docker-ce安装教程-阿里巴巴开源镜像站 # ste…...

MySQL常用练手题目
数据库表名和字段设计 1.学生表 Student(s_id,s_name,s_birth,s_sex) 学生编号,学生姓名, 出生年月,学生性别 2.课程表 Course(c_id,c_name,t_id) 课程编号, 课程名称, 教师编号 3.教师表 Teacher(t_id,t_name) 教师编号,教师姓名 4.成绩表 Score (s_id,c_id,s_score) 学生编号…...

Oracle字段长度不足位数补零
Oracle字段长度不足位数补零 有时候从数据库中取出的月份值是1,而不是01,该怎么办呢 SELECTLPAD( CODE_MONTH, 2, 0 ) FROMtb_cube_TY001 WHERECODE_BM_MEATYPE TY20 AND code_measure MYLX01 AND code_month <> ~ AND CODE_ENTITY 01A AND…...
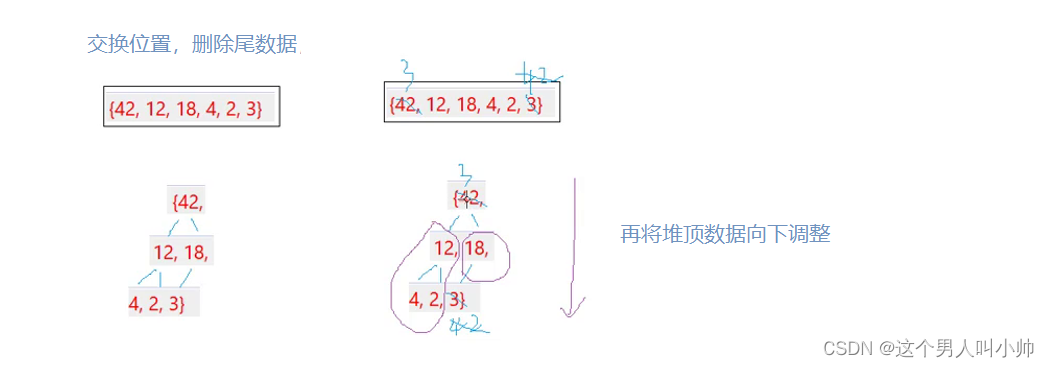
<数据结构与算法>二叉树堆的实现
目录 前言 一、树的概念及结构 1 树的概念 2 树的相关概念 二、二叉树的概念及结构 1.二叉树的概念 2. 特殊的二叉树 3. 二叉树的性质 4.二叉树的存储结构 三、二叉树的顺序结构及实现 1.堆的性质 2.堆的插入 3.堆的实现 堆的结构体 HeapInit 初始化 HeapPush 插入 HeapPop 删…...

FPGA:RS编码仿真过程
FPGA:RS编码仿真过程 RS码是一种纠错性能很强的线性纠错码,能够纠正随机错误和突发错误。RS码是一种多进制BCH码,能够同时纠正多个码元错误。 之前已经记录了在MATLAB中进行rs编解码的过程,现在利用FPGA的IP核实现RS编码的过程&…...
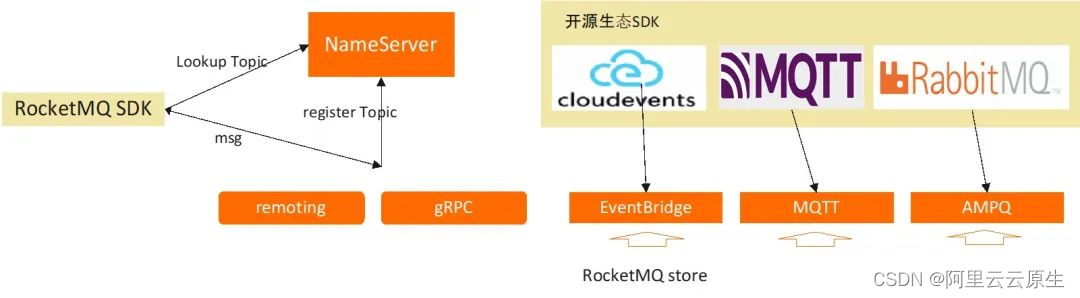
RocketMQ 5.0 架构解析:如何基于云原生架构支撑多元化场景
作者:隆基 本文将从技术角度了解 RocketMQ 的云原生架构,了解 RocketMQ 如何基于一套统一的架构支撑多元化的场景。 文章主要包含三部分内容。首先介绍 RocketMQ 5.0 的核心概念和架构概览;然后从集群角度出发,从宏观视角学习 R…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
