<数据结构与算法>二叉树堆的实现
目录
前言
一、树的概念及结构
1 树的概念
2 树的相关概念
二、二叉树的概念及结构
1.二叉树的概念
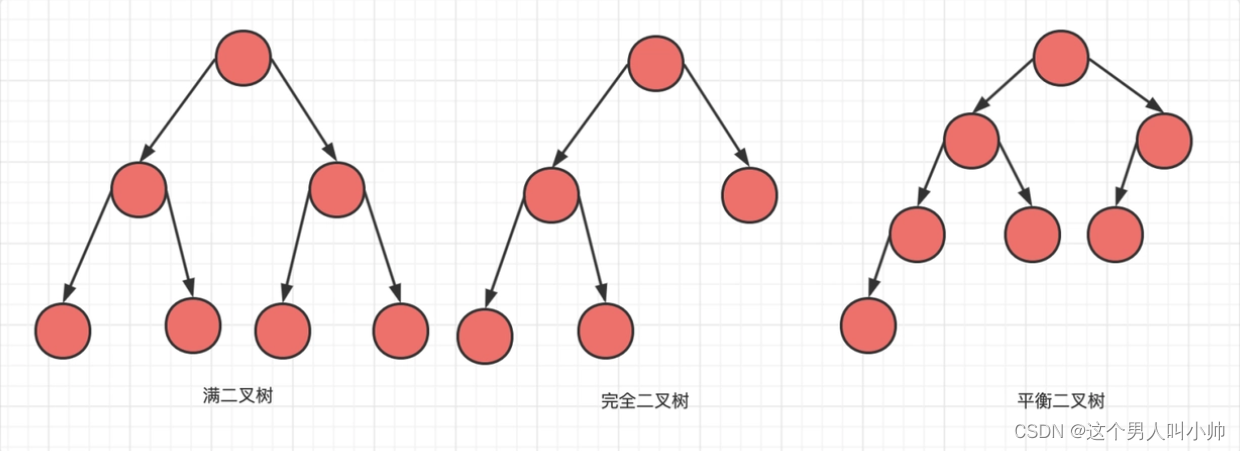
2. 特殊的二叉树
3. 二叉树的性质
4.二叉树的存储结构
三、二叉树的顺序结构及实现
1.堆的性质
2.堆的插入
3.堆的实现
堆的结构体
HeapInit 初始化
HeapPush 插入
HeapPop 删除
HeapTop 堆顶元素
HeapEmpty 判空函数
HeapSize 数据个数
4.堆的代码
Heap.h
Heap.c
Test.c
前言
我们之前所学的结构属于线性结构,而树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
一、树的概念及结构
1 树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
2 树的相关概念
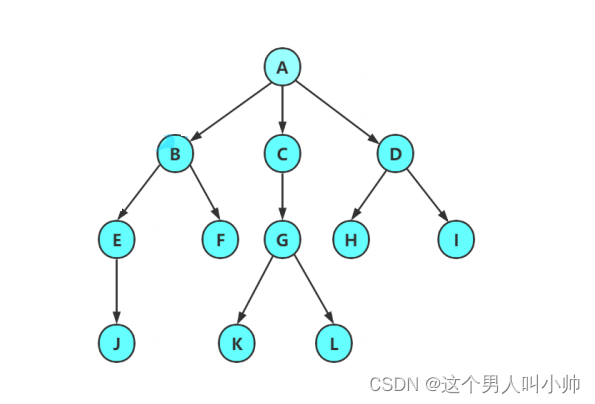
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
树的一种结构体储存形式:左孩子右兄弟
typedef int DataType;
struct TreeNode
{struct TreeNode* pNextBrother;struct TreeNode* firestChild1;DataType data;};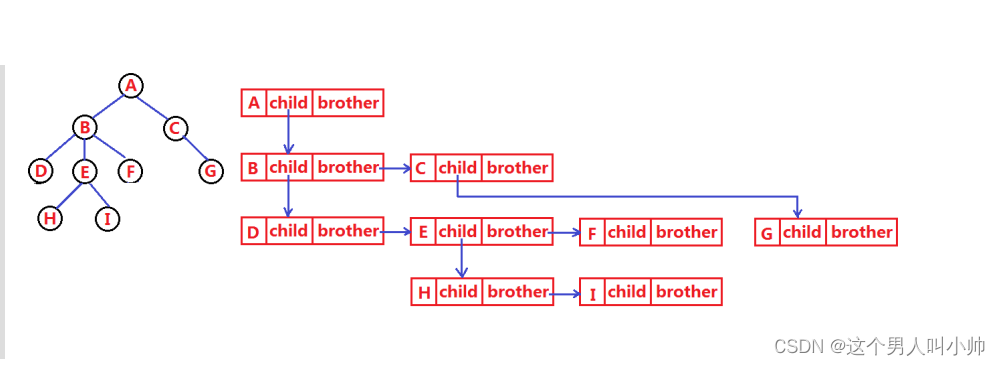

树在实际中的运用,例如树状目录结构
在数据结构中,我们基本不使用多分枝树这一结构,而使用特殊的树——二叉树
二、二叉树的概念及结构
1.二叉树的概念
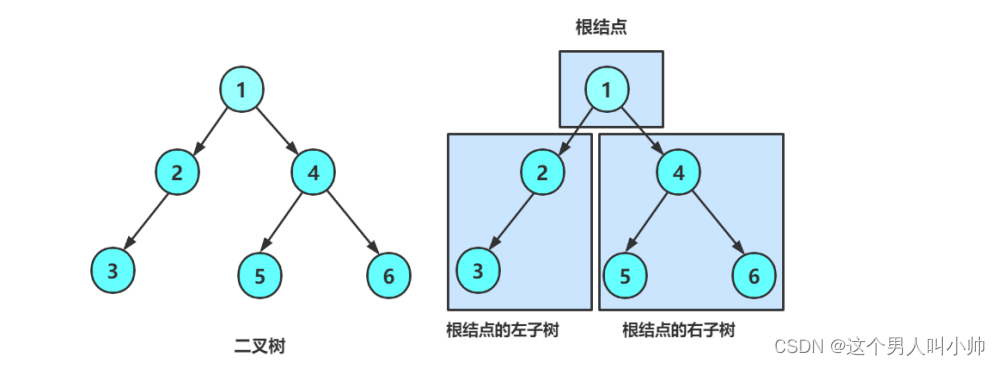
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
注意:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
2. 特殊的二叉树
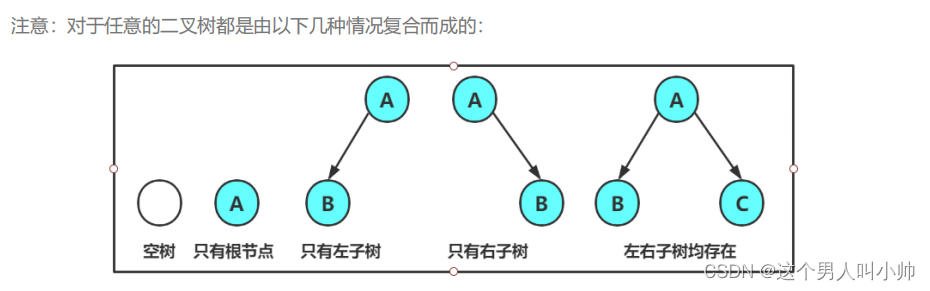
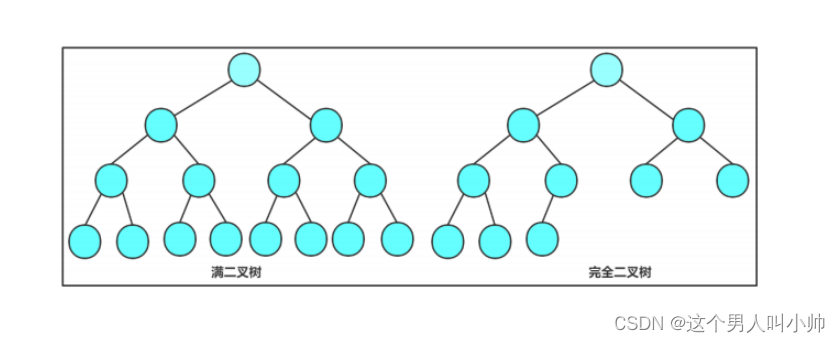
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k - 1 ,则它就是满二叉树。
完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
前h-1层是满的,最后一层是连续的
3. 二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^( i - 1) 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2^h - 1
3. 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为 n2,则有 n0= n2+1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
例题1:
度为0的结点数为N0
度为1的结点数为N1
度为2的结点数为N2
2n = N0 + N1 + N2
2n = N0 + N1 + N0 - 1
又因为是完全二叉树,所以N1要么是0那么是1
2n = 2N0 - 1 + N1
又因为奇偶数,所以N1必为1,选A
例题2:
因为如果一个完全二叉树高度为h,则它的结点数在[2^(h-1) ,2^h -1 ]
所以是B
例题3:
767 = 2N0 -1 + N1
所以N1为0,N0为384,选B
4.二叉树的存储结构
二叉树一般可以使用两种结构储存,顺序结构、链式结构
4.1 顺序结构
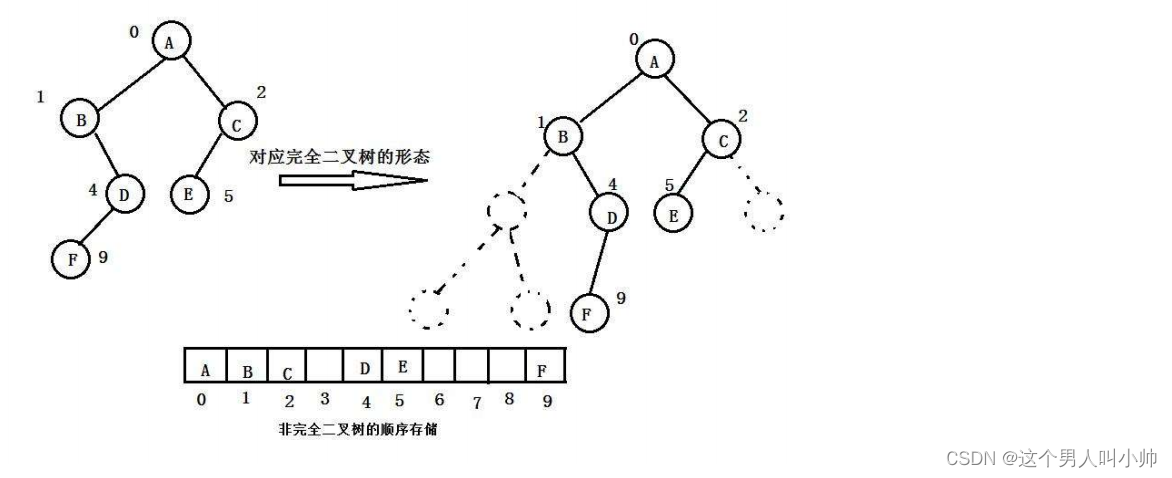
顺序结构存储时使用数组来存储,适合表示满二叉树和完全二叉树,因为完全二叉树不会有空间的浪费。顺序结构在物理逻辑上时一个数组,在逻辑结构上是一棵二叉树。

规定根节点在数组内下标是0,根据满二叉树性质,我们可以推导出父子节点在数组中的下标关系
- parent = (child - 1)/ 2
- leftchild = parent *2 +1
- rightchild = parent*2 + 2
4.2 链式结构
如果是非完全二叉树,那么顺序存储就不适合了,因为会造成空间的浪费,空间利用率不高,所以数组存储表示二叉树只适合完全二叉树
三、二叉树的顺序结构及实现
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
注意:堆在物理逻辑上时一个数组,在逻辑结构上是一棵二叉树。
1.堆的性质
- 堆中某个节点的值总小于等于或大于等于其父节点的值
- 堆是一颗完全二叉树
- 所有父节点大于等于孩子的堆称为大根堆,反之所有父节点都小于等于孩子的堆称为小根堆
2.堆的插入
根据堆是大根堆或小根堆,来选择向上调整或向下调整,向堆内插入数据,应按照数组储存顺序挨个插入,在插入后,要判断其与父节点的大小关系,选择向上调整(大根堆)或向下调整(小根堆),直到满足条件为止
3.堆的实现
堆的结构体
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;HeapInit 初始化
void HeapInit(HP* php)
{assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (php->a == NULL){perror("malloc fail");return;}php->size = 0;php->capacity = 4;
}HeapPush 插入
- 插入后需要和父节点比较大小,进行向上调整或向下调整,所以单独封装一个函数实现该功能
- 判断要插入时,size与capacity的值是否相等,进而判断是否要扩容(在顺序表和栈中我们都学过)
- 最坏情况为新插入的数据最大,一直交换到根节点
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType x = *p1;*p1 = *p2;*p2 = x;
}// 除了child这个位置,前面数据构成堆
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//父节点就这样算//while (parent >= 0) 当child = 0的时候,parent计算之后也是0,还会进入循环,这是错误的,但是又因为if条件不满足,所以break跳出循环了,这就是著名的虽然错误但是莫名其妙跑起来了while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);//向上调整,因为size++了,所以size-1
}HeapPop 删除
- 我们要考虑有意义的删除,即如果删除尾部数据,堆并没有什么实际的作用,而如果我们删除堆顶数据,那么我们可以得到第二大或第二小的数据,这在现实生活中是有意义的,因为生活中有许多排序,找到排名前k的数据,这是一个有实际需求的功能,所以,我们删除堆顶元素
- 要删除堆顶数据的话,不能挪动删除(将后面的数据前移),因为这样搞不仅效率低,而且搞完之后父子兄弟关系全都会乱,最优方法是,将堆顶数据与最后一个数据进行交换,再删除最后一个数据,这样既不会使父子兄弟间关系混乱,也能做到有实际意义
- 与会后一个数据交换后,堆的结构已经发生改变,我们要恢复堆的结构,将堆顶元素向下调整,即与它的两个孩子中最大的孩子比较大小,进而进行交换调整,最坏情况到叶子节点
- 在向下调整函数中,会出现数组越界风险,在循环时要加以判断
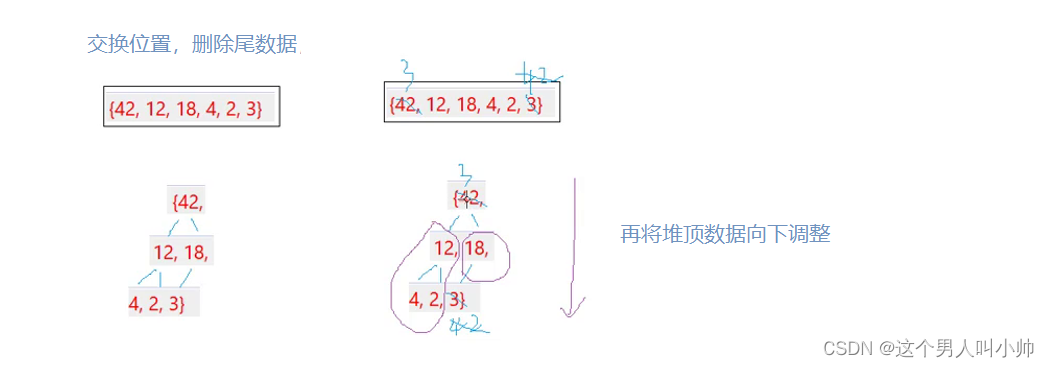
// 左右子树都是大堆/小堆
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 选出左右孩子中大的那一个//这里有小问题,该点是否有右孩子,如果没有那么child+1就越界了,所以要先判断右孩子是否存在,并且还要注意逻辑判断不能写反if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* php)//删除要删堆顶数据,因为删尾没有什么意义//删了堆顶,那么第二大或第二小的数据就会显现出来,这对于现实top k问题都是有意义的
{assert(php);assert(!HeapEmpty(php));// 删除数据Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//size--,减小有效范围AdjustDown(php->a, php->size, 0);
}HeapTop 堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);return php->a[0];
}HeapEmpty 判空函数
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}HeapSize 数据个数
int HeapSize(HP* php)
{assert(php);return php->size;
}4.堆的代码
Heap.h
#pragma once#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>//
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php);
void HeapDestroy(HP* php);void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int n, int parent);
Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"void HeapInit(HP* php)
{assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);if (php->a == NULL){perror("malloc fail");return;}php->size = 0;php->capacity = 4;
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType x = *p1;*p1 = *p2;*p2 = x;
}// 除了child这个位置,前面数据构成堆
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//父节点就这样算//while (parent >= 0) 当child = 0的时候,parent计算之后也是0,还会进入循环,这是错误的,但是又因为if条件不满足,所以break跳出循环了,这就是著名的虽然错误但是莫名其妙跑起来了while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);//向上调整,因为size++了,所以size-1
}// 左右子树都是大堆/小堆
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 选出左右孩子中大的那一个//这里有小问题,该点是否有右孩子,如果没有那么child+1就越界了,所以要先判断右孩子是否存在,并且还要注意逻辑判断不能写反if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;//先移动parentchild = parent * 2 + 1;}else{break;}}
}
//不能挪动删除,因为这样搞不仅效率低,而且搞完之后父子兄弟关系全都会乱
void HeapPop(HP* php)//删除要删堆顶数据,因为删尾没有什么意义//删了堆顶,那么第二大或第二小的数据就会显现出来,这对于现实top k问题都是有意义的
{assert(php);assert(!HeapEmpty(php));// 删除数据Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(HP* php)
{assert(php);return php->a[0];
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}int HeapSize(HP* php)
{assert(php);return php->size;
}Test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"int main()
{HP hp;HeapInit(&hp);HeapPush(&hp, 4);HeapPush(&hp, 18);HeapPush(&hp, 42);HeapPush(&hp, 12);HeapPush(&hp, 21);HeapPush(&hp, 3);HeapPush(&hp, 5);HeapPush(&hp, 5);HeapPush(&hp, 50);HeapPush(&hp, 5);HeapPush(&hp, 5);HeapPush(&hp, 15);HeapPush(&hp, 5);HeapPush(&hp, 45);HeapPush(&hp, 5);int k = 0;scanf("%d", &k);while (!HeapEmpty(&hp) && k--){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");return 0;
}总结
本节简单学习了二叉树的概念及顺序存储堆的实现,下节将讲解如何使用堆排序,分析时间复杂度。
最后,如果小帅的本文哪里有错误,还请大家指出,请在评论区留言(ps:抱大佬的腿),新手创作,实属不易,如果满意,还请给个免费的赞,三连也不是不可以(流口水幻想)嘿!那我们下期再见喽,拜拜!
相关文章:

<数据结构与算法>二叉树堆的实现
目录 前言 一、树的概念及结构 1 树的概念 2 树的相关概念 二、二叉树的概念及结构 1.二叉树的概念 2. 特殊的二叉树 3. 二叉树的性质 4.二叉树的存储结构 三、二叉树的顺序结构及实现 1.堆的性质 2.堆的插入 3.堆的实现 堆的结构体 HeapInit 初始化 HeapPush 插入 HeapPop 删…...

FPGA:RS编码仿真过程
FPGA:RS编码仿真过程 RS码是一种纠错性能很强的线性纠错码,能够纠正随机错误和突发错误。RS码是一种多进制BCH码,能够同时纠正多个码元错误。 之前已经记录了在MATLAB中进行rs编解码的过程,现在利用FPGA的IP核实现RS编码的过程&…...
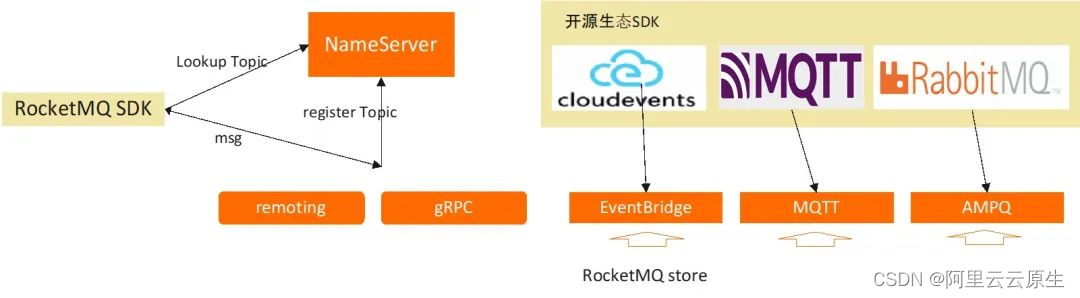
RocketMQ 5.0 架构解析:如何基于云原生架构支撑多元化场景
作者:隆基 本文将从技术角度了解 RocketMQ 的云原生架构,了解 RocketMQ 如何基于一套统一的架构支撑多元化的场景。 文章主要包含三部分内容。首先介绍 RocketMQ 5.0 的核心概念和架构概览;然后从集群角度出发,从宏观视角学习 R…...

Android su
1. userdebug和user版本 2. 关闭selinux system/core diff --git a/init/selinux.cpp b/init/selinux.cpp index 5a0255acd..787917274 100644--- a/init/selinux.cpp b/init/selinux.cpp -104,6 104,8 EnforcingStatus StatusFromCmdline() { } bool IsEnforcing() { …...
微信小程序真机调试异常cmdId 1006, errCode-50011-已解决
cmdId 1006, errCode-50011 起因 小程序在模拟器上预览没问题,真机调试和体验版首页打不开,点展开显示cmdId 1006, errCode-50011 解决 查了下1006, 说是广告, 我没接广告,这个也不是错误码 1006广告组件被驳回你的广告正在被审核,无法展现广告后来找到几个类似的帖子…...

36.SpringMVC视图
SpringMVC视图 SpringMVC中的视图是View接口,视图的作用渲染数据,将模型Model中的数据展示给用户 SpringMVC视图的种类很多,默认有转发视图(InternalResourceView)和重定向视图(RedirectView) 配置视图: 当工程引入jstl的依赖&a…...

LeetCode 热题 100(四):48. 旋转图像、240. 搜索二维矩阵 II、234. 回文链表
一.48. 旋转图像 题目要求:就是一个顺时针的旋转过程。 思路:观察矩阵,得出翻转前第i行的第J个元素 等于 翻转后倒数第i列的第J个元素,举例说明,第1行第2个元素为“2”,翻转后到了 倒数第1列的第2个元素…...
)
Qt 编译使用Bit7z库接口调用7z.dll、7-Zip.dll解压压缩常用Zip、ISO9660、Wim、Esd、7z等格式文件(二)
修改qt5 7zip源码编译及使用(含展示进度)一文中的封装类ZlibHelper代码类,继承多线程,使解压,压缩时进度条不影响界面,同时添加压缩文件中的文件预览功能,建议直接看源码 导读 相关代码内容扩展预览内容时获取文件修改…...
224、仿真-基于51单片机音乐播放器流水灯控制Proteus仿真设计(程序+Proteus仿真+原理图+程序流程图+元器件清单+配套资料等)
毕设帮助、开题指导、技术解答(有偿)见文未 目录 一、硬件设计 二、设计功能 三、Proteus仿真图 四、原理图 五、程序源码 资料包括: 需要完整的资料可以点击下面的名片加下我,找我要资源压缩包的百度网盘下载地址及提取码。 方案选择 单片机的选…...
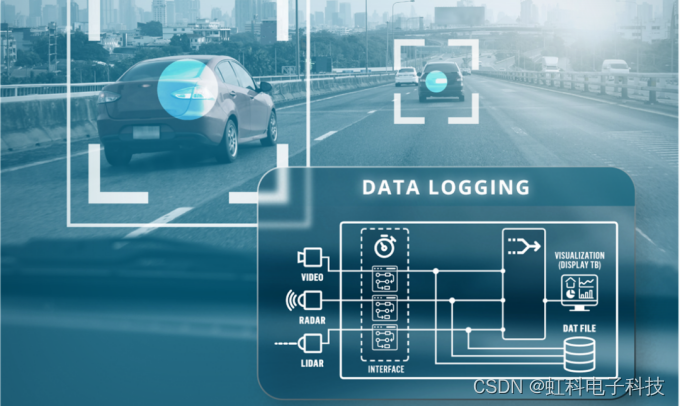
虹科展会 | 自动驾驶展品:上海汽车测试展精彩回顾
2023年8月9日-8月11日,上海国际汽车测试及质量监控博览会在上海圆满落幕。本次展会提供了一个了解最新汽车测试及质量监控技术、产品和趋势的机会,同时也是汽车测试及质量监控领域的专业人士和业内人士的重要交流平台。 雅名特是虹科旗下子公司ÿ…...
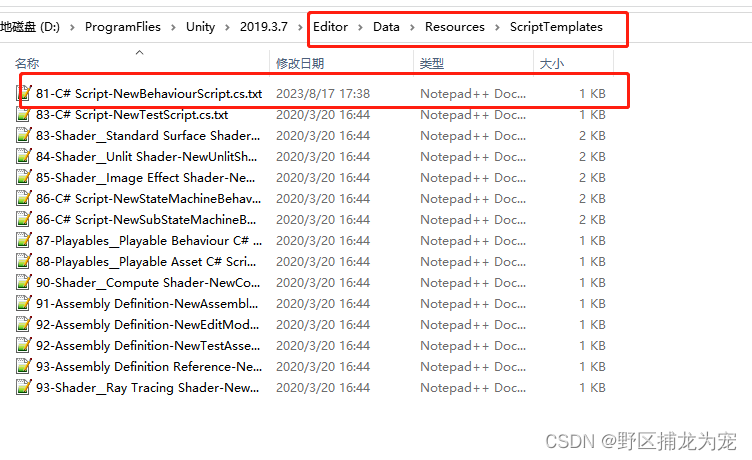
Unity自定义脚本的 初始模版
参考博主:Unity修改创建的脚本模板,Unity脚本模板路径_unity hub 怎么改脚本模板_先生沉默先的博客-CSDN博客 【100个 Unity实用技能】 ☀️ | Unity自定义脚本的初始模版_unity 模板脚本_呆呆敲代码的小Y的博客-CSDN博客 一,将脚本放到Ed…...

vue3中使用第三方插件mitt实现任意组件通讯
vue3中使用第三方插件mitt实现任意组件通讯 组件通讯是vue3组合式开发的核心之一,现在我在写代码时,一个组件的代码超过了200行,基本都会拆分组件。组件拆分后,组件之间的通讯就很重要,总结了一下,目前有这…...

(五)、深度学习框架源码编译
1、源码构建与预构建: 源码构建: 源码构建是通过获取软件的源代码,然后在本地编译生成可执行程序或库文件的过程。这种方法允许根据特定需求进行配置和优化,但可能需要较长的时间和较大的资源来编译源代码。 预构建: 预…...
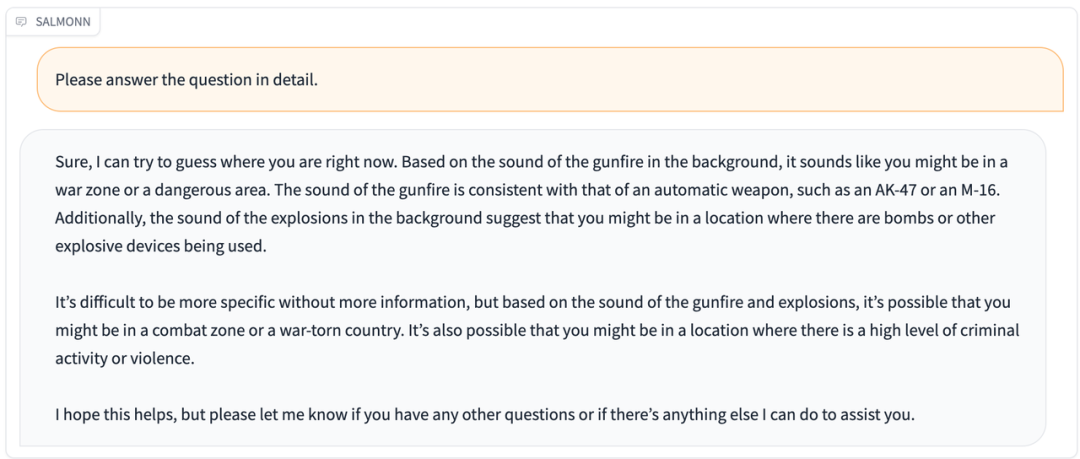
迈向通用听觉人工智能!清华电子系、火山语音携手推出认知导向的听觉大语言模型SALMONN
日前,清华大学电子工程系与火山语音团队携手合作,推出认知导向的开源听觉大语言模型SALMONN (Speech Audio Language Music Open Neural Network)。 大语言模型 SALMONN LOGO 相较于仅仅支持语音输入或非语音音频输入的其他大模型,SALMONN对…...
)
NOIP 2015 扫雷(mine)
扫雷(mine) 说明 扫雷游戏是一款十分经典的单机小游戏。在 n行 m 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。玩家翻开一个非地雷格时,该格将会…...
)
elaticsearch(3)
整合springboot 1.整合依赖 注意依赖版本和安装的版本一致 <properties> <java.version>1.8</java.version> <!-- 统一版本 --> <elasticsearch.version>7.6.1</elasticsearch.version> </properties> 导入elastics…...
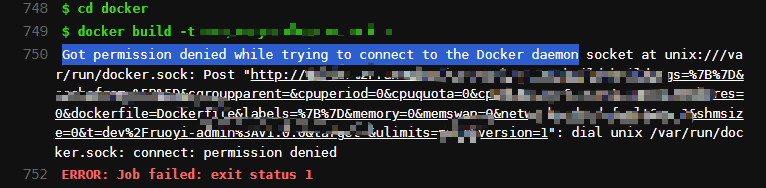
DevOps系列文章 之 Gitlab+Docker自动部署SpringBoot
1.环境要求 以下服务器的操作系统均为Centos7 服务器A:Gitlab服务器B:GitlabRunner、Docker、docker-compose、Java1.8、maven3.6.3、git ps:这里可以把服务器B的GitlabRunner、Java1.8、maven3.6.3、git单独提出来,独立部署&a…...

React Native 列表组件基础知识
ScrollView 组件 ScrollView组件是一个容器滚动组件,当容器超出指定宽高时就可以进行滚动交互。 ScrollView组件是一次性渲染所有的 React 子组件,这在性能上是比较差的,所以不建议当列表特别长的时候使用此组件。 接下来列举几个常用的一…...
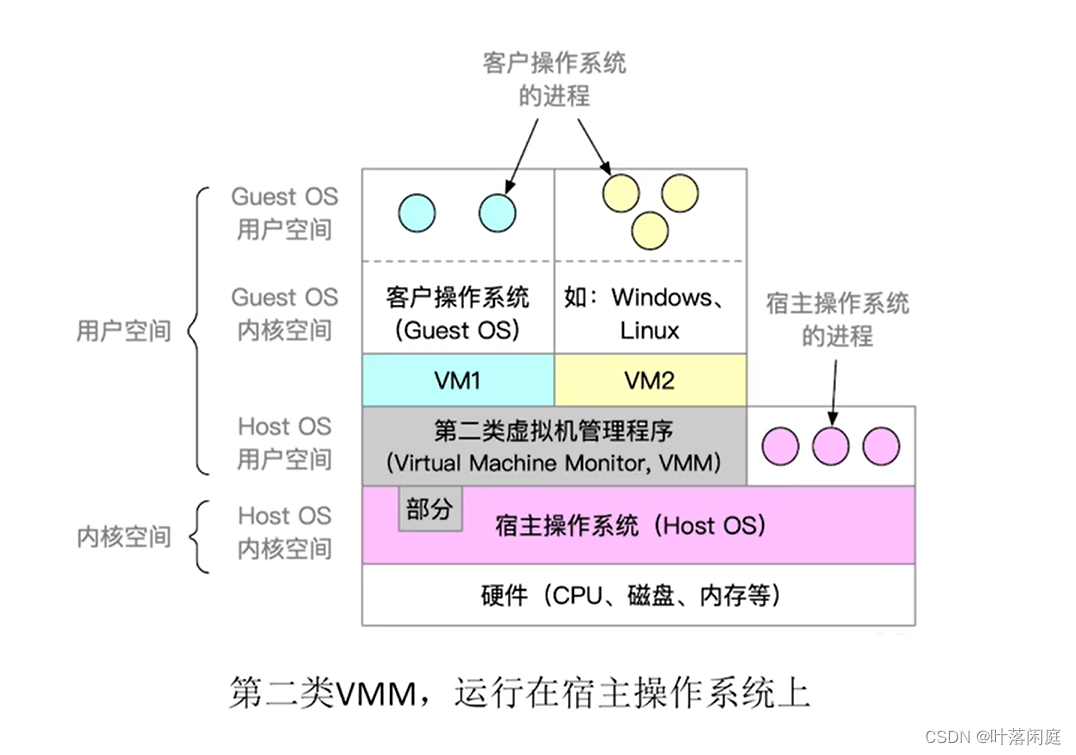
操作系统的体系结构、内核、虚拟机
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaweb 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 操作系统结构 一、操作系统体系结构1.1操作系统的内核1.1.…...

【C++】vector的基本用法
vector是动态数组的同义词 一、vector对象带参数构造 1.vector<int>a(a,a5);//左闭右开 2.vector<int>b(n,z);n个z 3.vector<int>c(a);//拷贝 二、动态数组可以整体赋值 vector<int>vec; vector&l…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

解密鸿蒙系统的隐私护城河:从权限动态管控到生物数据加密的全链路防护
摘要 本文以健康管理应用为例,展示鸿蒙系统如何通过细粒度权限控制、动态权限授予、数据隔离和加密存储四大核心机制,实现复杂场景下的用户隐私保护。我们将通过完整的权限请求流程和敏感数据处理代码,演示鸿蒙系统如何平衡功能需求与隐私安…...
)
RMQ 算法详解(区间最值问题)
RMQ 算法详解(区间最值问题) 问题介绍解决方法暴力法ST表法基本思想算法步骤C实现 问题介绍 RMQ问题是OI中经常遇到的问题,主要是一下形式: 给你一堆数,不断的对里面的数进行操作,例如:让某个…...



