【3Ds Max】车削命令的简单使用(以制作花瓶为例)
简介
在3ds Max中,"车削"(Lathe)是一种建模命令,用于创建围绕轴线旋转的几何形状。通过车削命令,您可以将一个闭合的平面或曲线几何形状旋转,从而生成一个立体对象。这种方法常用于创建圆柱体、杯子、碗、花瓶等中空或实心的形状。
以下是使用3ds Max中的车削命令的基本步骤:
-
创建基本形状: 首先,您需要创建一个闭合的平面或曲线形状,作为车削的基础。这可以是一个多边形,或者是使用线段工具创建的曲线。
-
选择要车削的形状: 在场景中选择您要进行车削操作的闭合形状。在编辑模式下,您可以使用选择工具(Selection Tool)来选择这个形状。
-
激活车削命令: 在3ds Max的主菜单中,选择 "修改" > "车削",或者您也可以使用快捷键 "Ctrl + L" 来激活车削命令。
-
设置车削参数: 在车削对话框中,您可以设置以下参数:
- 旋转角度(Angle): 这是要围绕轴线旋转的角度。
- 分段数(Segments): 您可以设置车削后的几何的分段数,以控制其光滑程度。
- 轴心点(Axis Center): 您可以选择轴心点的位置,通常是对象的中心或其他位置。
-
预览车削效果: 在对话框中预览车削效果,根据需要调整参数,直到达到您想要的效果为止。
-
应用车削: 点击“确定”按钮后,3ds Max会将车削效果应用于选定的闭合形状,从而创建一个围绕轴线旋转的立体对象。
-
编辑车削: 车削后,您仍然可以通过选择车削对象并重新打开车削对话框来调整车削参数。
总的来说,车削是一个基本的建模操作,用于创建旋转体的几何形状。
示例(创建一个花瓶模型)
1. 首先创建一个花瓶贴图的平面,注意平面的长宽应当和图片尺寸保持一致。
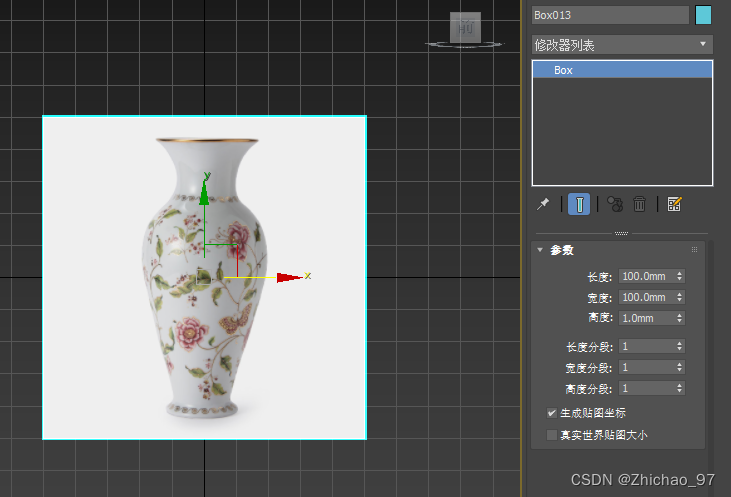
2. 为了让鼠标不会捕捉到这个平面,我们可以冻结该平面
选择“对象属性”
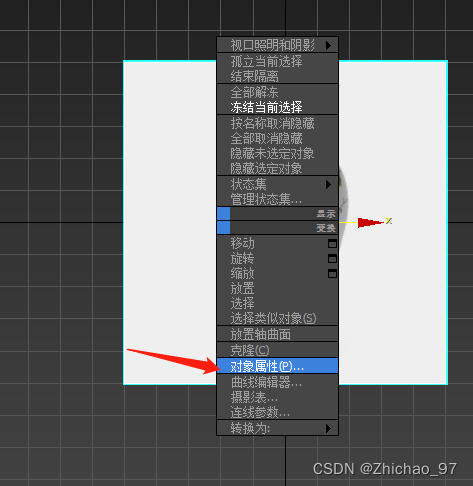
取消勾选“以灰色显示冻结对象”,勾选“冻结”

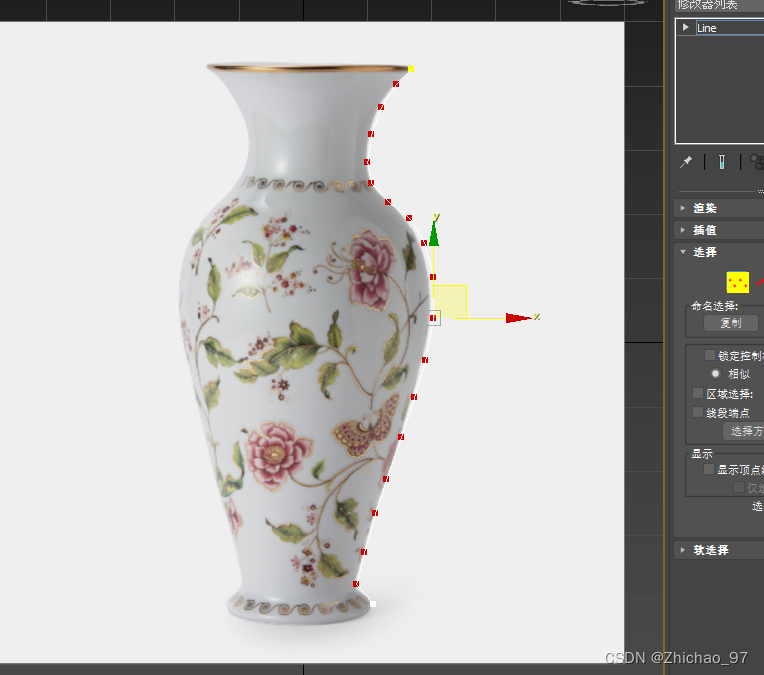
3. 通过线描绘出花瓶的侧边轮廓,这里由于白线看不清我就画了一个红线来表示
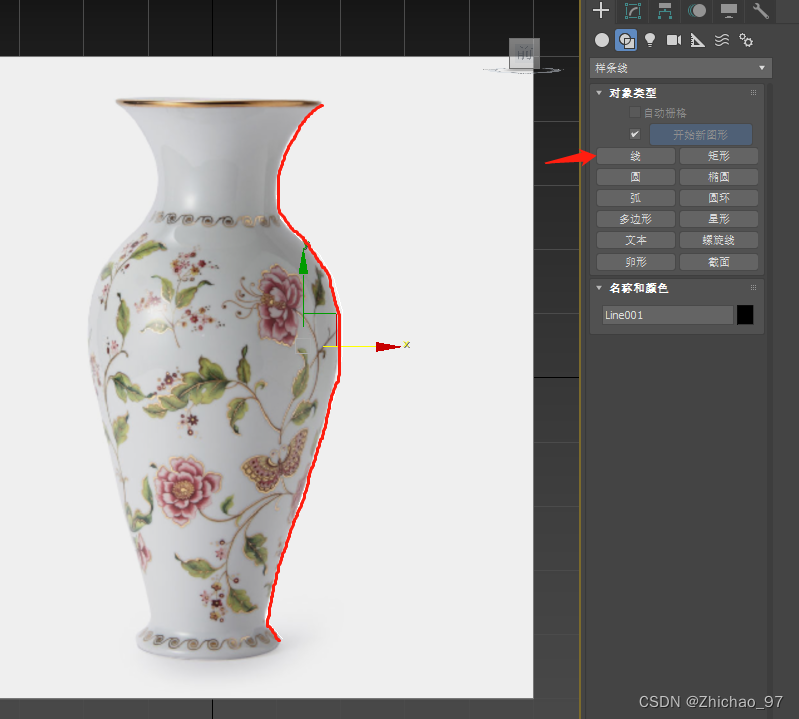
4. 将勾勒的线条转换为可编辑样条线
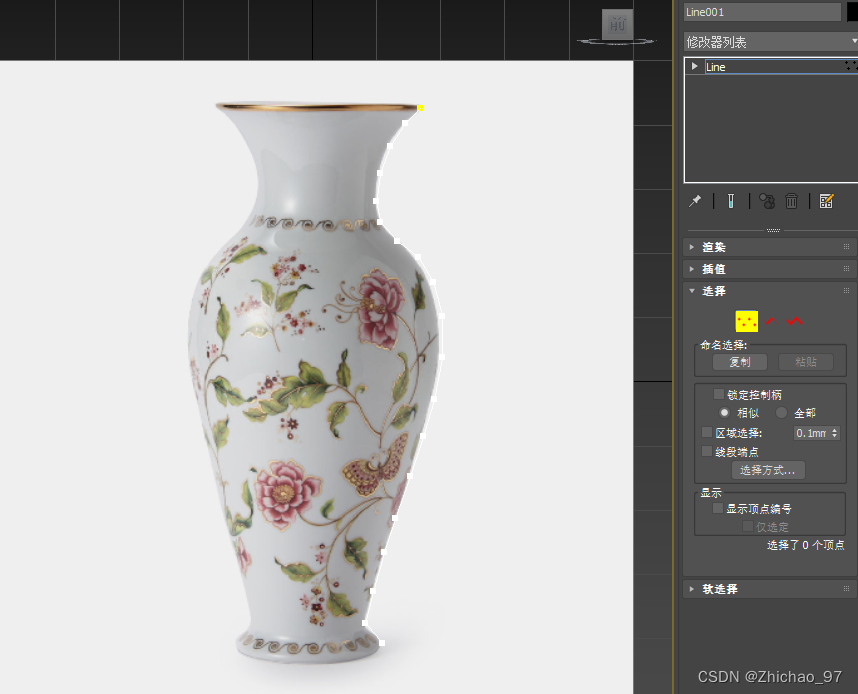
5. 选中需要平滑处理的点
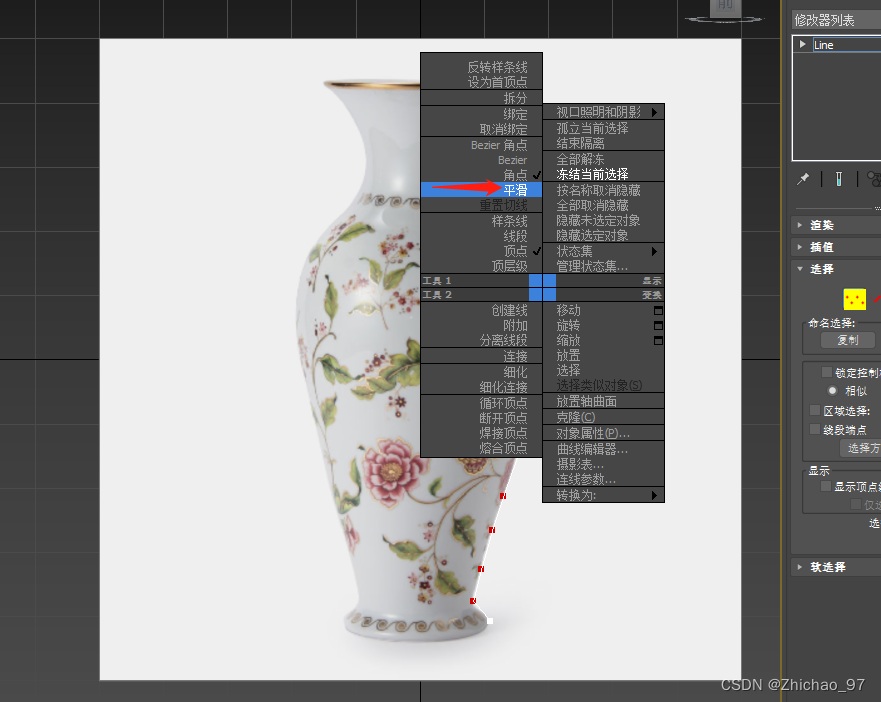
4. 选择“平滑”选项,这样可以自动对我们选择的这些点所构成的线条进行平滑处理(如果是对精度要求比较高的情况,可以选择“Bezier角点”,从而单独对每一个点进行处理)
5. 平滑后还需要我们单独对点的位置进行细微的调整

6. 对于像下图的情况,我们可以点击“细化”来添加点

点击鼠标右键,然后选择“细化”
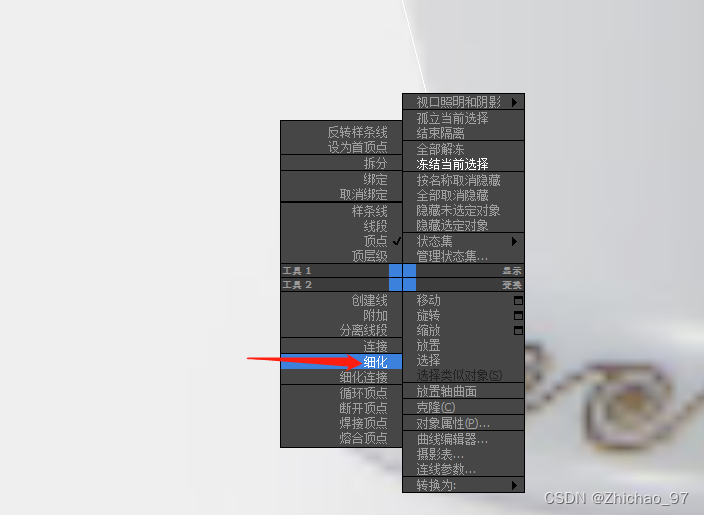
或点击“优化”

来在需要加点的地方加点

可以将点转化为Bezier角点进行调整
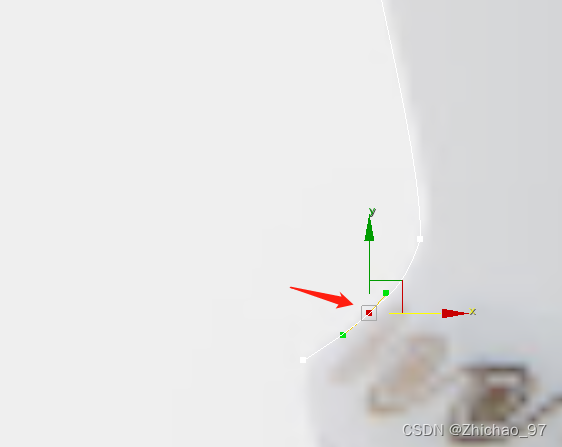
7. 在选择线条的前提下,在修改器列表点击“车削”
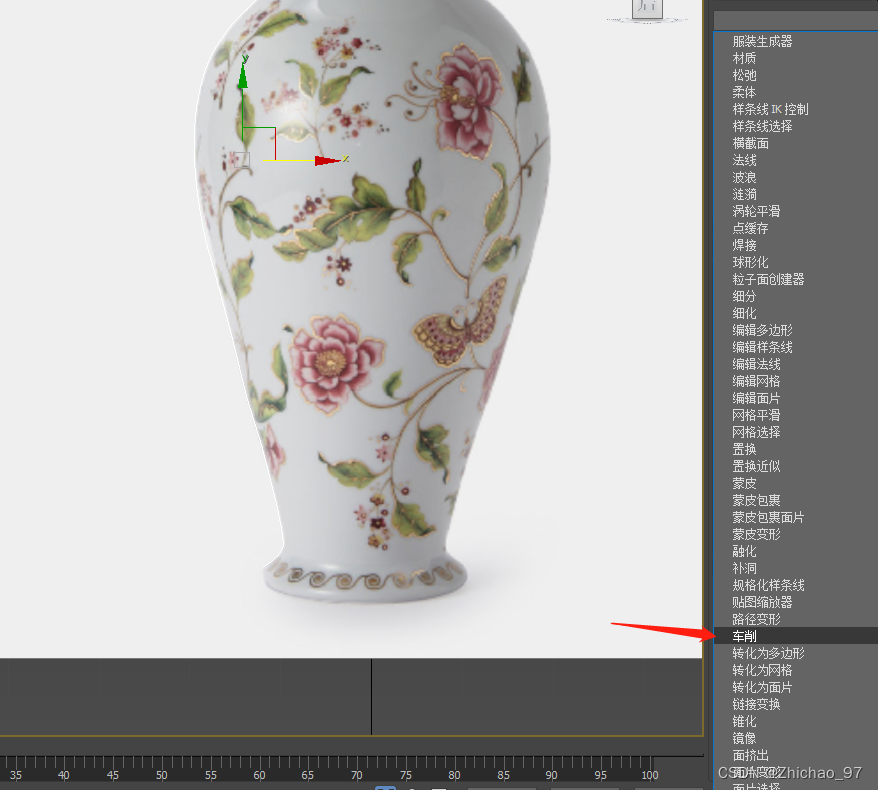
8. 选择“轴”
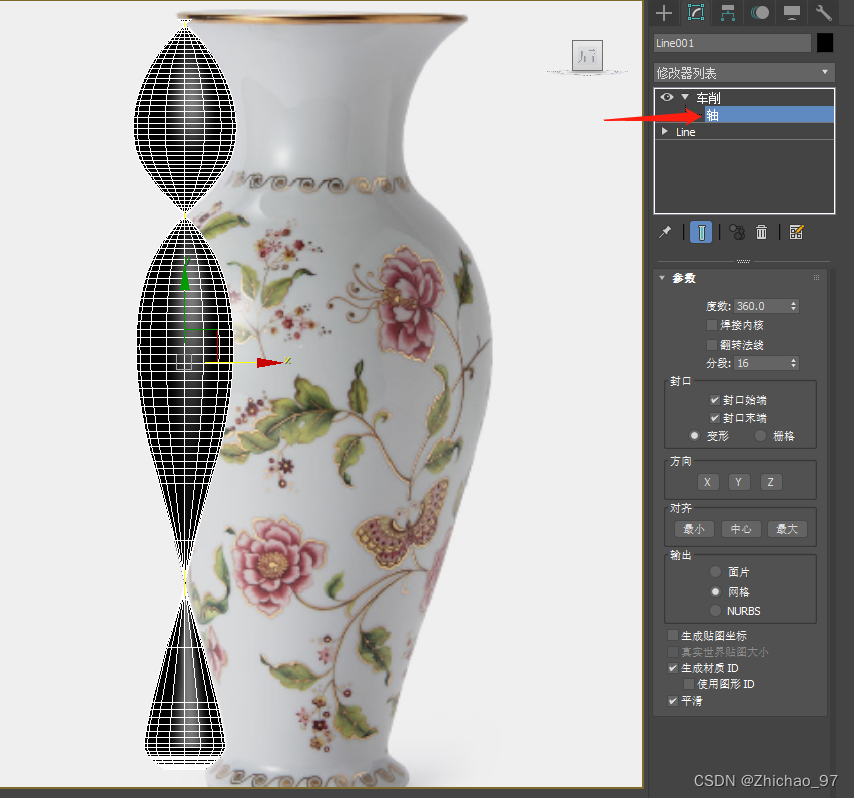
将轴沿x轴平移至花瓶的中心
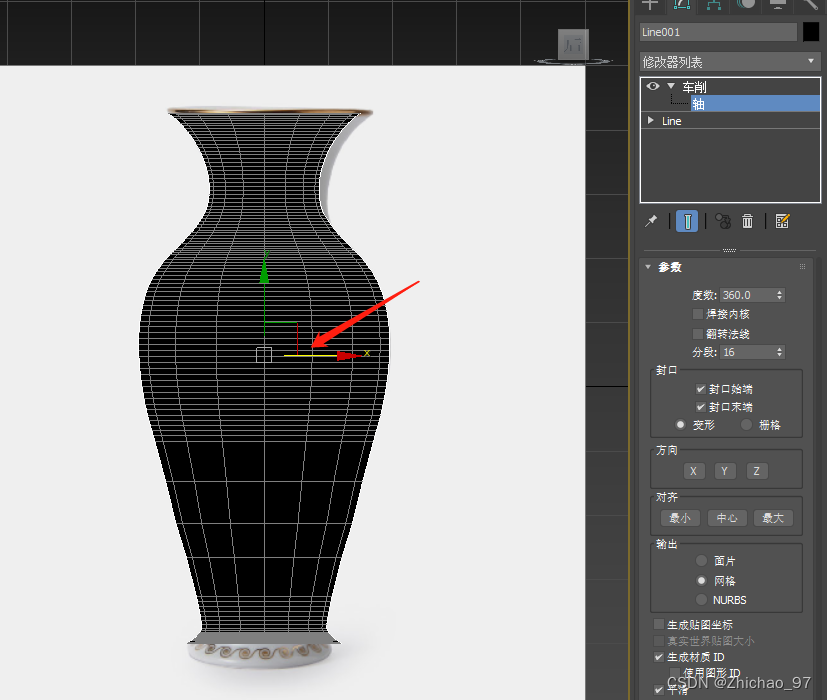
9. 接下来看看车削命令的常用参数的功能
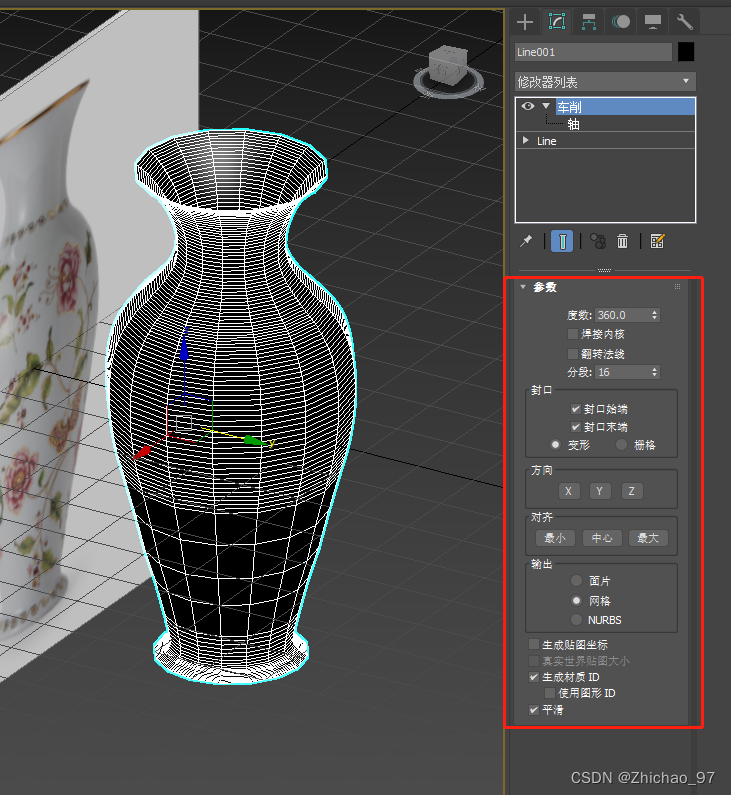
首先是度数,如果我们调整成180°,效果如下
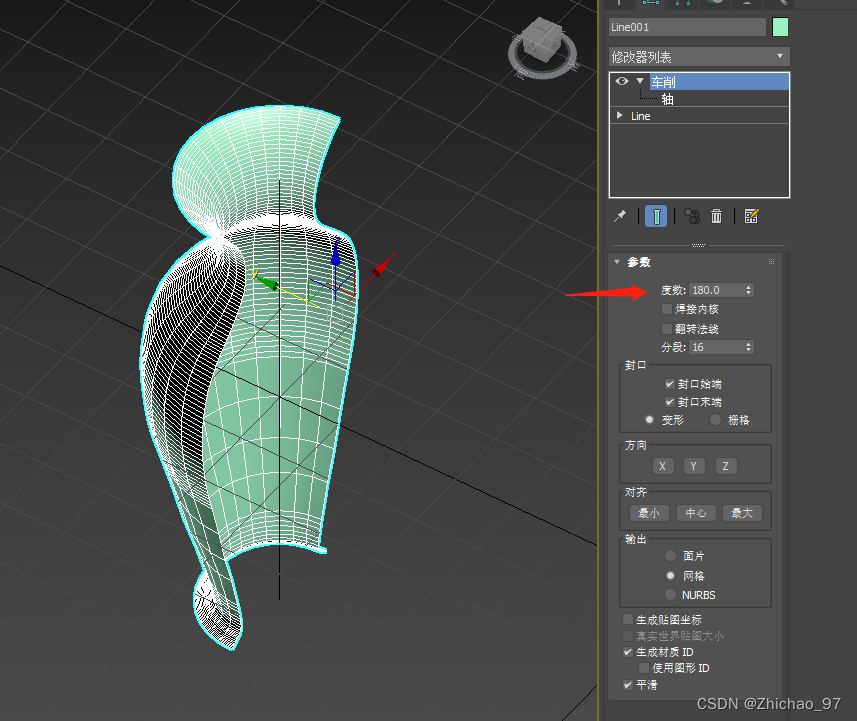
分段,假如这里我们分别设置为3和30,看一下效果
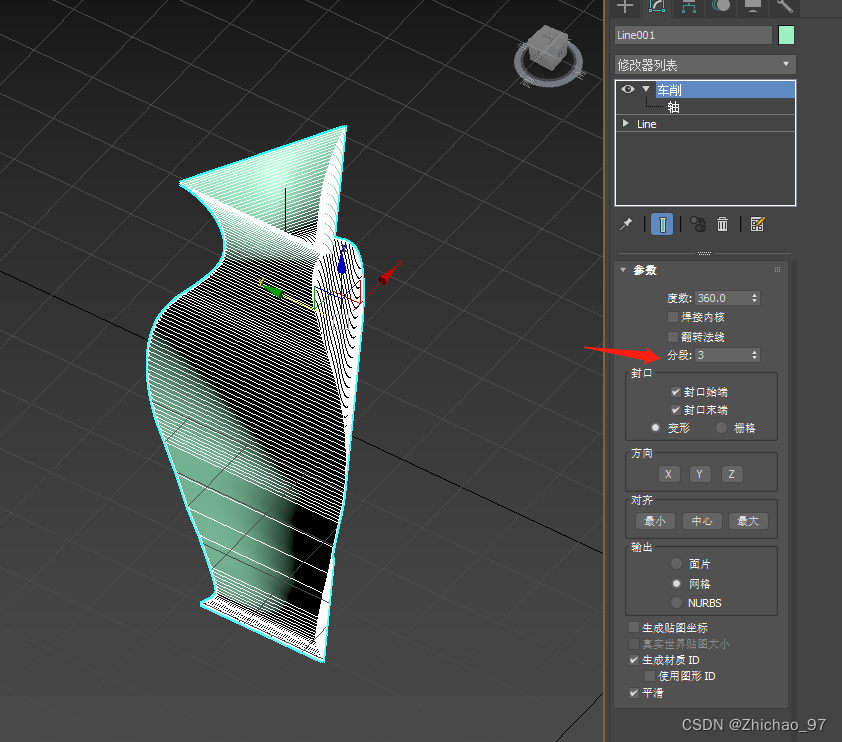
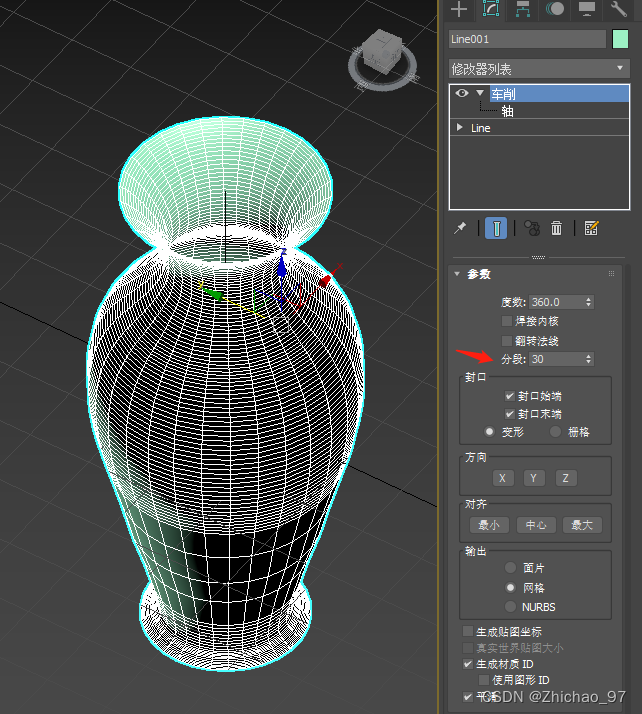
翻转法线:
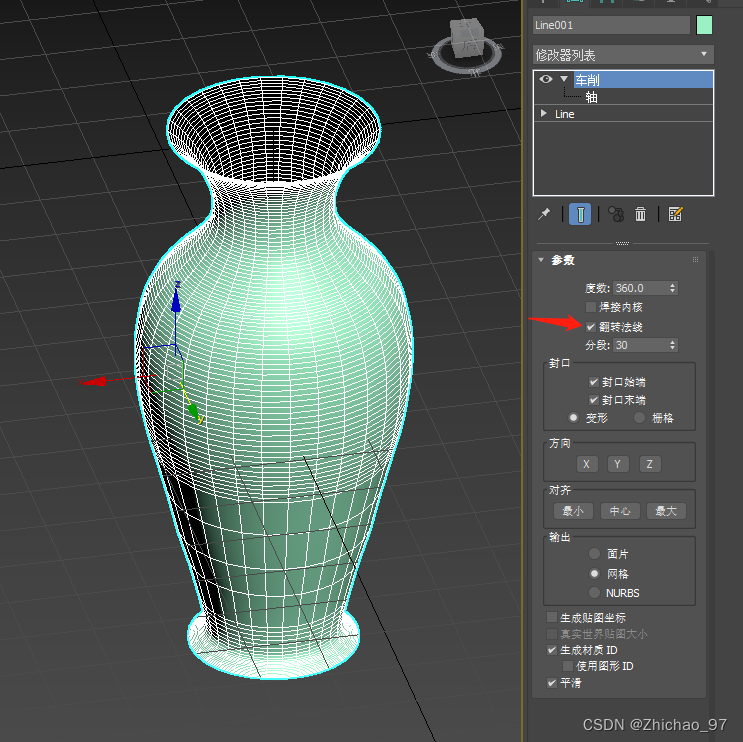
10. 目前花瓶是没有厚度的,我们先回到样条线层级
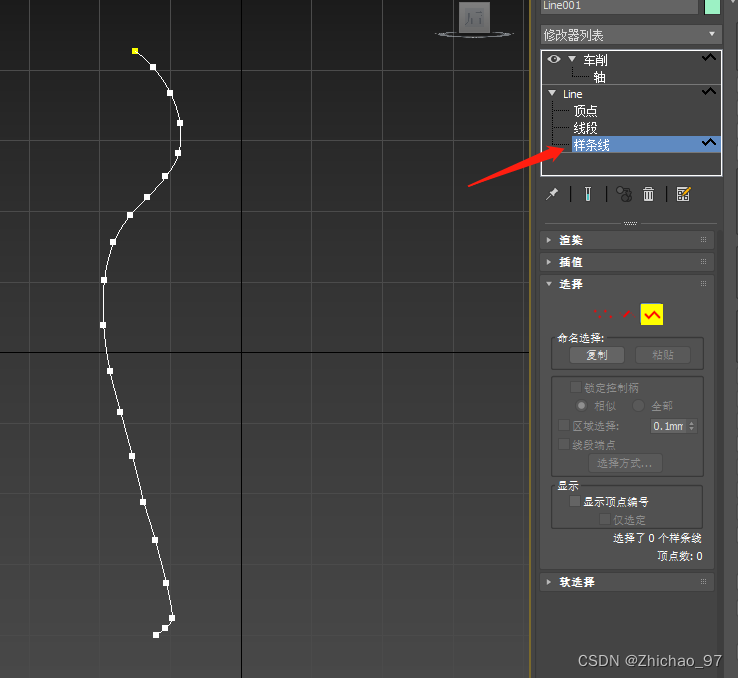
给其一个轮廓
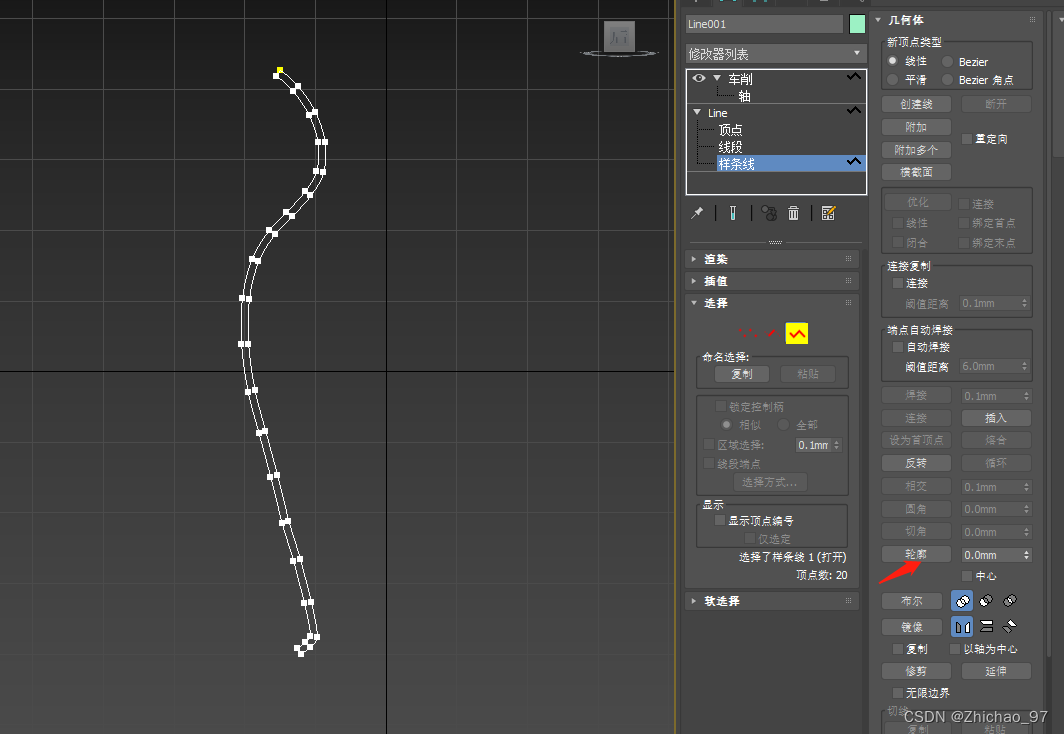
再进入车削层级,取消“翻转法线”
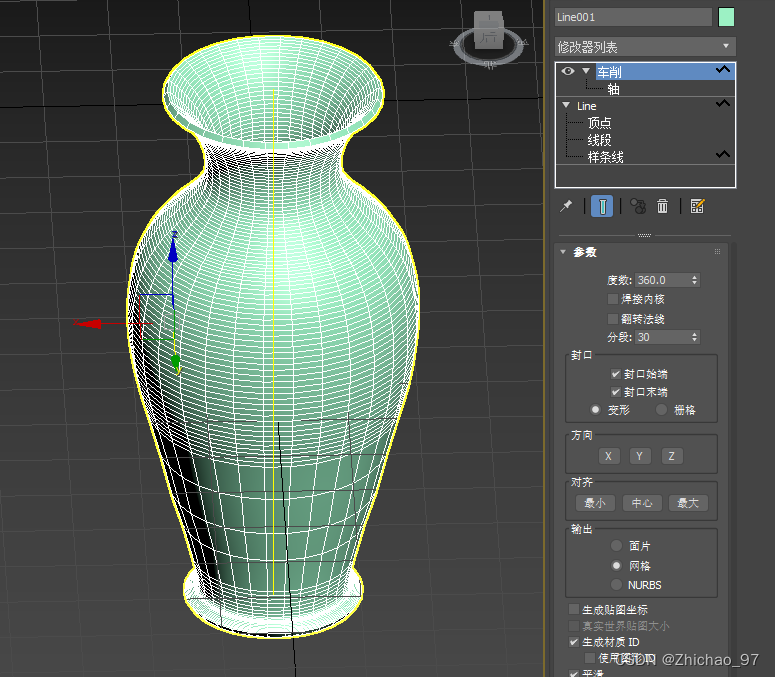
相关文章:

【3Ds Max】车削命令的简单使用(以制作花瓶为例)
简介 在3ds Max中,"车削"(Lathe)是一种建模命令,用于创建围绕轴线旋转的几何形状。通过车削命令,您可以将一个闭合的平面或曲线几何形状旋转,从而生成一个立体对象。这种方法常用于创建圆柱体、…...
Python 3 使用HBase 总结
HBase 简介和安装 请参考文章:HBase 一文读懂 Python3 HBase API HBase 前期准备 1 安装happybase库操作hbase 安装该库 pip install happybase2 确保 Hadoop 和 Zookeeper 可用并开启 确保Hadoop 正常运行 确保Zookeeper 正常运行3 开启HBase thrift服务 使用命…...

Maven方式构建SpringBoot项目
目录 1、创建maven项目 2、添加springboot相关依赖 3、配置启动端口 4、修改APP文件 5、配置controller 6、启动应用 1、创建maven项目 项目如下: 2、添加springboot相关依赖 <parent><groupId>org.springframework.boot</groupId><arti…...
不花一分钱,利用免费电脑软件将视频MV变成歌曲音频MP3
教程 1.点击下载电脑软件下载地址,点击下载,安装。(没有利益关系,没有打广告,只是单纯教学) 2.安装完成后,点击格式工厂 3.然后如图所示依次,点击【音频】->【-MP3】 3.然后点击…...
触达用户的几种方式)
运营知识之用户运营(一)触达用户的几种方式
运营知识之用户运营(一)触达用户的几种方式 APP推送短信(DeepLink/Deferred DeepLink):短信拉起app电子邮件 EDM电话/外呼(人工、AI)电话外呼加短信(操作步骤短链)微信生…...

cocos creator pageView 循环展示 广告牌功能
在使用 creator pageView 滑动到最大或者最小为止的时候 滑动不了没法流畅的运行到最开始或者最后那个界面 循环展示 1.策划大人有需要就是要循环流畅的展示 解决方案: 做预制件的时候 最第一个界面之前 做一个最后的界面放到最前边去 比如 1,2,3,4,5,6,7,8 修改成 8,1…...
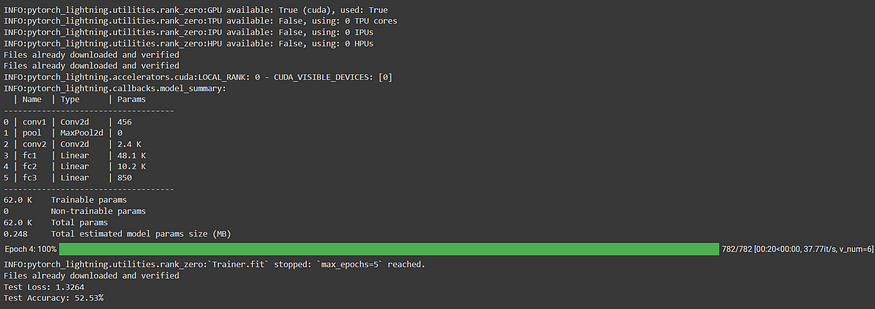
PyTorch Lightning:通过分布式训练扩展深度学习工作流
一、介绍 欢迎来到我们关于 PyTorch Lightning 系列的第二篇文章!在上一篇文章中,我们向您介绍了 PyTorch Lightning,并探讨了它在简化深度学习模型开发方面的主要功能和优势。我们了解了 PyTorch Lightning 如何为组织和构建 PyTorch 代码提…...

无涯教程-Perl - splice函数
描述 此函数从LENGTH元素的OFFSET元素中删除ARRAY元素,如果指定,则用LIST替换删除的元素。如果省略LENGTH,则从OFFSET开始删除所有内容。 语法 以下是此函数的简单语法- splice ARRAY, OFFSET, LENGTH, LISTsplice ARRAY, OFFSET, LENGTHsplice ARRAY, OFFSET返回值 该函数…...
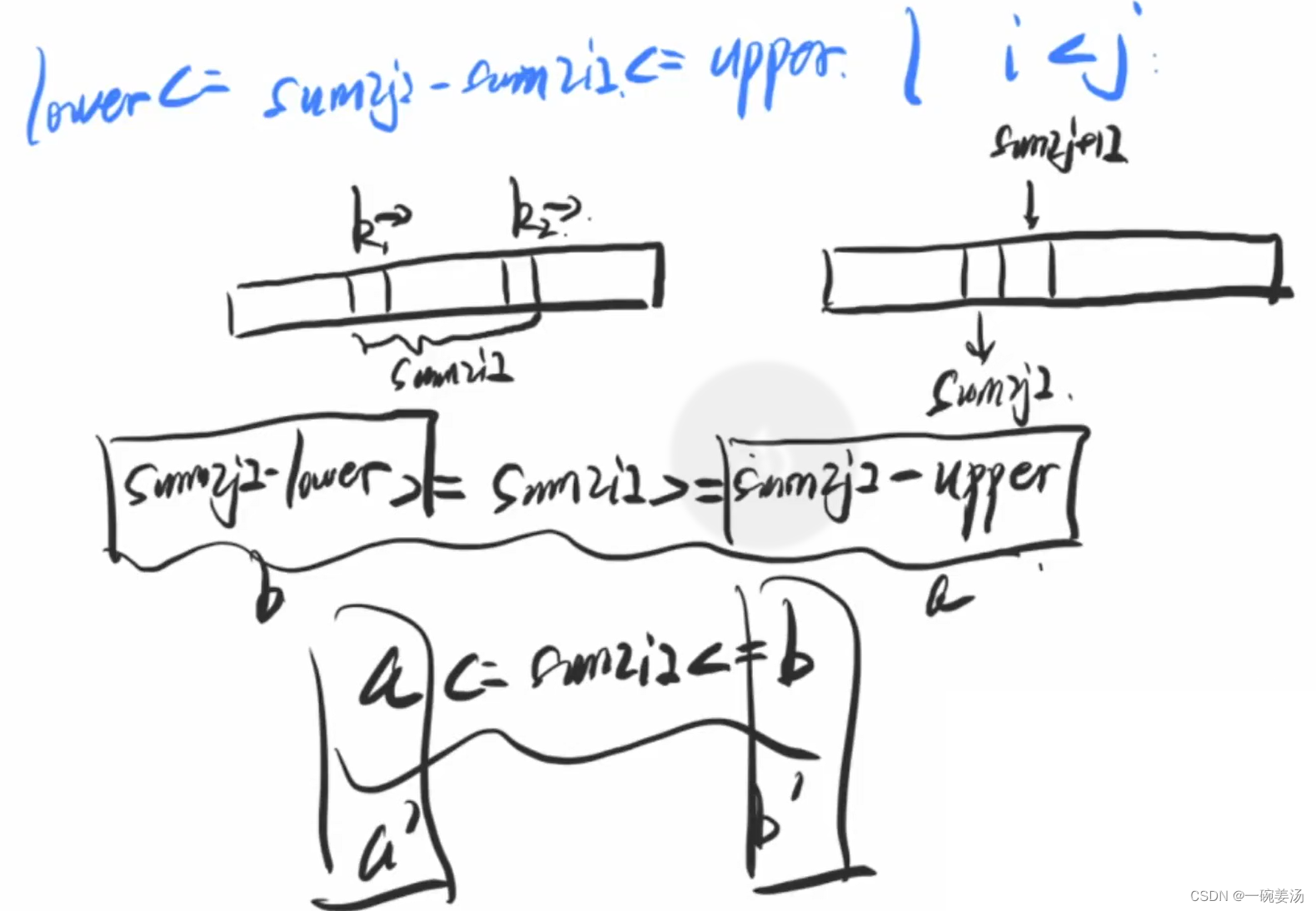
归并排序:从二路到多路
前言 我们所熟知的快速排序和归并排序都是非常优秀的排序算法。 但是快速排序和归并排序的一个区别就是:快速排序是一种内部排序,而归并排序是一种外部排序。 简单理解归并排序:递归地拆分,回溯过程中,将排序结果进…...

【Vue】运行项目报错 This dependency was not found
背景 运行Vue 项目报错,提示This dependency was not found;然后我根据提示 执行 npm install --save vue/types/umd ,执行后发现错误,我一开始一直以为是我本地装不上这个依赖。后来找了资料后,看到应该是自己的代码里面随意的i…...

Shell编程之正则表达式
文本处理器:三剑客:grep查找sed awk shell正则表达式由一类特殊字符以及文本字符所编写的一种模式,处理文本当中的内容,其中的一些字符不表示字符的字面含义表示一种控制或者通配的功能 通配符:匹配文件名和目录名&a…...
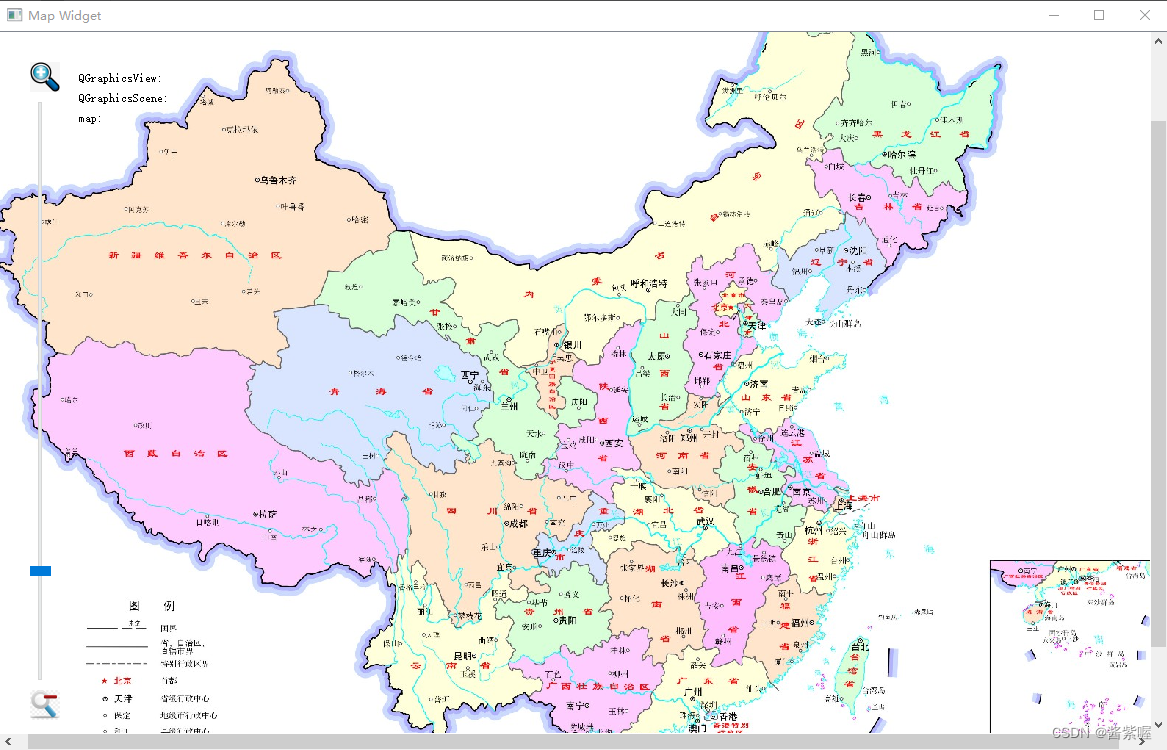
QGraphicsView 实例3地图浏览器
主要介绍Graphics View框架,实现地图的浏览、放大、缩小,以及显示各个位置的视图、场景和地图坐标 效果图: mapwidget.h #ifndef MAPWIDGET_H #define MAPWIDGET_H #include <QLabel> #include <QMouseEvent> #include <QGraphicsView&…...
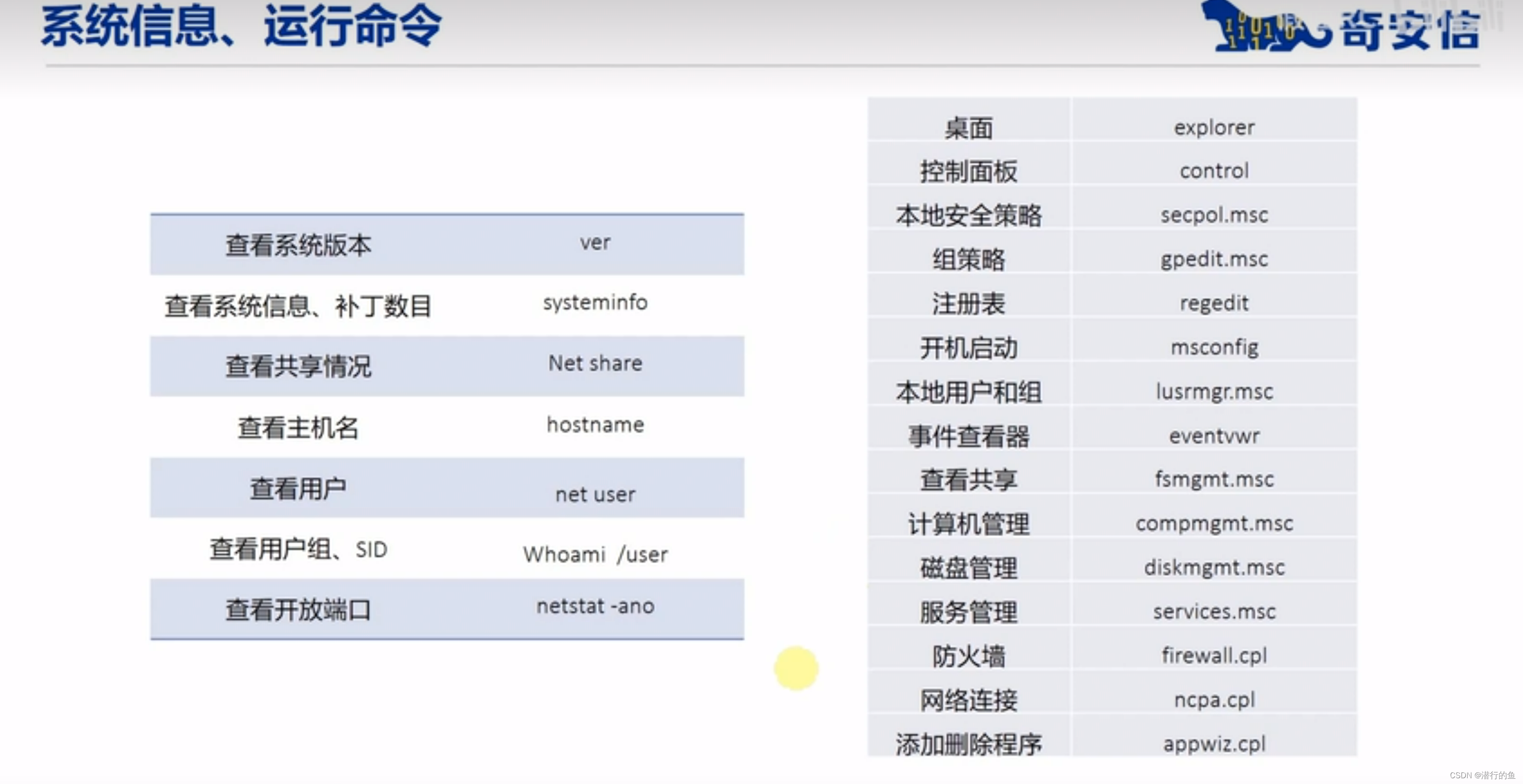
Windows基础安全知识
目录 常用DOS命令 ipconfig ping dir cd net user 常用DOS命令 内置账户访问控制 Windows访问控制 安全标识符 访问控制项 用户账户控制 UAC令牌 其他安全配置 本地安全策略 用户密码策略复杂性要求 强制密码历史: 禁止密码重复使用 密码最短使用期限…...

自定义注解和自定义注解处理器来扫描所有带有某个特定注解的Controller层
在Spring Boot中,您可以使用自定义注解和自定义注解处理器来扫描所有带有某个特定注解的Controller层。 以下是一个简单的示例,演示如何实现这个功能: 首先,创建自定义注解 CustomAnnotation ,用于标记需要被扫描的C…...

浏览器渲染原理 - 输入url 回车后发生了什么
目录 渲染时间点渲染流水线1,解析(parse)HTML1.1,DOM树1.2,CSSOM树1.3,解析时遇到 css 是怎么做的1.4,解析时遇到 js 是怎么做的 2,样式计算 Recalculate style3,布局 la…...

大文本的全文检索方案附件索引
一、简介 Elasticsearch附件索引是需要插件支持的功能,它允许将文件内容附加到Elasticsearch文档中,并对这些附件内容进行全文检索。本文将带你了解索引附件的原理和使用方法,并通过一个实际示例来说明如何在Elasticsearch中索引和检索文件附…...
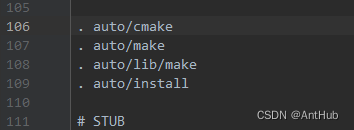
35_windows环境debug Nginx 源码-CLion配置CMake和启动
文章目录 生成 CMakeLists.txt 组态档35_windows环境debug Nginx 源码-CLion配置CMake和启动生成 CMakeLists.txt 组态档 修改auto目录configure文件,在 . auto/make 上边增加 . auto/cmake, 大概在 106 行。在 auto 目录下创建cmake 文件其内容如下: #!/usr/bin/env bash NG…...

收集的一些比较好的git网址
1、民间故事 https://github.com/folkstory/lingqiu/blob/master/%E4%BC%A0%E8%AF%B4%E9%83%A8%E5%88%86/%E4%BA%BA%E7%89%A9%E4%BC%A0%E8%AF%B4/%E2%80%9C%E6%B5%B7%E5%BA%95%E6%8D%9E%E6%9C%88%E2%80%9D%E7%9A%84%E6%AD%A6%E4%B8%BE.md 2、童话故事 https://gutenberg.org/c…...
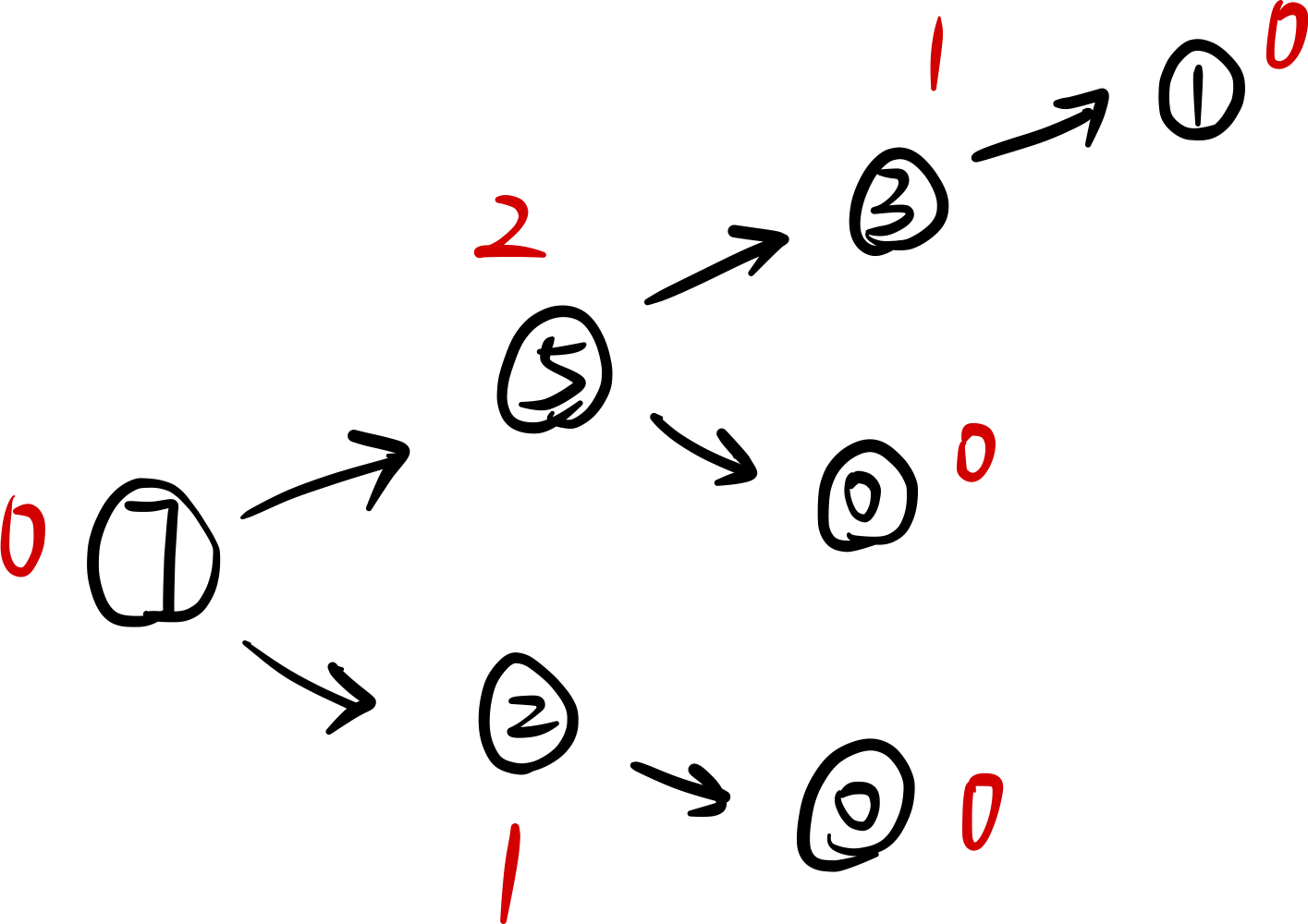
容斥原理 博弈论(多种Nim游戏解法)
目录 容斥原理容斥原理的简介能被整除的数(典型例题)实现思路代码实现扩展:用DPS实现 博弈论博弈论中的相关性质博弈论的相关结论先手必败必胜的证明Nim游戏(典型例题)代码实现 台阶-Nim游戏(典型例题&…...
【C++】函数指针
2023年8月18日,周五上午 今天在B站看Qt教学视频的时候遇到了 目录 语法和typedef或using结合我的总结 语法 返回类型 (*指针变量名)(参数列表)以下是一些示例来说明如何声明不同类型的函数指针: 声明一个不接受任何参数且返回void的函数指针…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
