【leetcode 力扣刷题】快乐数/可被k整除的最小整数(可能存在无限循环的技巧题)
可能存在无限循环的技巧题
- 202. 快乐数
- 数学分析
- 1015. 可被k整除的最小整数
- 数学分析
202. 快乐数
题目链接:202. 快乐数
题目内容:
 理解题意,快乐数就是重复每位数的平方之和得到的新数的过程,最终这个数能变成1。变成1以后,即便重复上述过程,也一直是1的循环,因此在重复得到新数的过程中,如果这个数等于1就停止。
理解题意,快乐数就是重复每位数的平方之和得到的新数的过程,最终这个数能变成1。变成1以后,即便重复上述过程,也一直是1的循环,因此在重复得到新数的过程中,如果这个数等于1就停止。
问题:如果始终变不到1呢?题目中提到无限循环但始终变不到1,无限循环就意味着重复,如果重复找新数的过程中得到的数p在之前是出现过的,那么之后找到的数到下一次找到p前,都是重复出现的,直到变成p以后又继续循环。因此每次得到一个新数都要判断之前是否出现过,如果出现过就终止过程,返回false。
查找这个数是否出现过,用什么数据结构? 哈希表!【快速查找一个元素是否存在】 用什么实现哈希表呢?前面的题目有用到数组、set和map。 对于此题,一个数n,将其每位数求平方再相加这个重复过程中会得到多少种数是不确定的,因此不能用数组;map存<key,value>此题我们不需要value,只需要key,因此直接用set。
每次得到一个新数首先判断其每位数平方之后是否为1,是直接返回true;如果不是再判断这个数是否已经出现在set中,如果是,直接返回false;如果不是重复寻找新数的过程并重复上述判断。
代码如下(C++):
class Solution {
public://对整数n每位数求平方再相加求和的过程int getsum(int n){int sum = 0;while(n){sum+= (n%10) * (n%10);n= n/10;}return sum;}bool isHappy(int n) {//存出现过的数unordered_set<int> count;int sum = getsum(n);//每位数平方和不等于1才进入循环,找新数//如果等于1,即为快乐数while(sum != 1){//如果已经存在过,就进入循环了if(count.count(sum))return false;else count.insert(sum);//找新数sum = getsum(sum);} return true;}
};
数学分析
一个数不是快乐数,那么就进入无限循环,但是万一这个循环内的数字特别大特别多呢?
力扣这道题的官方题解中,分析了9,99,……,9999999等这些共i位数字的最大的情况,各位平方求和后的数字:
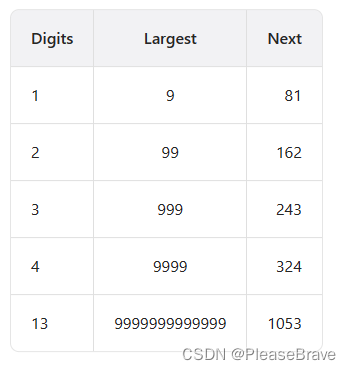
题目中n<=2^31-1,也就是2147483648-1,最多10的10次方,而只有13位的数字,其各位平方之和才能上千。就算各位数平方之和达到了四位数,再求和一次就变成了三位数,再求和一次就变成了243以内。因此再大的数字经过各位数平方求和操作后,大小都会迅速下降,最终控制在243以内,要么进行循环,要么最终变成1。
所以实际上用数组实现哈希表也是可以的,初始化数组长度为243,元素全是0。代码如下(C++):
bool isHappy(int n) {//用数组存出现过的数字int count[243] = {0};int sum = getsum(n);//每位数平方和不等于1才进入循环,找新数//如果等于1,即为快乐数while(sum != 1){//如果已经存在过,就进入循环了if( sum<=243 && count[sum-1])return false;//注意控制下标不要越界if( sum<= 243 )count[sum-1]++;//找新数sum = getsum(sum);} return true;}
1015. 可被k整除的最小整数
题目链接:1015. 可被k整除的最小整数
题目内容:

理解题意:①正整数需要满足:能够被k整除的【即n%k=0】,仅包含数字1【比如11,1111,111…111等】;②满足①中的条件的n可能不止一个,那么要找其中最小的;③返回n的长度而不是数字n本身。
如何表示这样的n? 假设n初始化为1,然后逐渐增大n = n*10 + 1,直到找到n满足题意。但是这样的int类型的n最多只能有10位,继续增大n就超出了int类型的范围,即便是64位的带符号的整数(最大为18446744073709551616),n的长度也只有20。 因此不能直接用上式表示n,并且本题本身也不要求返回n而是n的长度。
解法
- 用余数r来代替n:
假设:n%k = r (即:n = k*i + r ,i≥1)
那么:n’%k = (n*10+1)%k = (k*i*10 +r*10 +1) %k = (r*10+1)%k
因此可以用 r*10+1代替n*10+1
并且因需要求出n的长度,不需要记录n,因此用余数r来代替n; - 如果无解就会出现循环,存在a>b(都是由数字1组成的),a%k = b%k ≠ 0,用哈希表(set)存出现过的余数,如果重复出现就表示进入循环无解:
【解法①】用哈希表存出现过的余数,如果再次出现说明进入循环无解:
class Solution {
public:int smallestRepunitDivByK(int k) {int res = 1 % k;int len = 1;//存出现过的余数unordered_set <int> set_res;//余数=0就不进入循环,直接返回结果while(res){//如果余数≠0且出现了重复,就直接返回if(set_res.count(res)) return -1;set_res.insert(res);res = (res * 10 + 1) % k;len++;}return len;}
};
【优化】实际上余数r的范围是0~k-1,总共k个数字,那么如果有解,循环k次内,一定会找到结果:
class Solution {
public:int smallestRepunitDivByK(int k) {int res = 1%k, len = 1;//最多循环k次for(int i = 0 ;i < k ;i++){if(!res) return len;res = (res*10 + 1)%k;len++; }return -1; }
};
数学分析
- 能够直观的知道k是否有解?
如果k是2或者5的倍数,因为n是奇数肯定不能被2整除,因为n的末尾是1而不是0或者5,肯定不能被5整除。 - 除2和5以外的k一定有解吗?
假设有全是1的数字a和b对k同余,即a%k = b%k ,那么(a - b)%k = 0,而a - b = 11…1100…00,可以表示成a - b = (11…11)*(10^x),k不等于2和5的倍数,即k和10是互质的,a-b能够整除k的话,只能是(11…11)能够整除k,11…11恰好全是由1构成的,即11…11就是解,因此k如果不是2和5的倍数,就一定有解。
代码实现(C++):因为k除2和5的倍数外一定有解,那么就一直寻找就行,直到余数=0
int smallestRepunitDivByK(int k) {//如果是2或者5的倍数无解直接返回-1if(k%2==0||k%5==0) return -1;//n=1,初始长度len=1 int len=1;//r表示余数,初始n=1,r=n%k=1%kint r=1%k;//只要余数r不为0,就没有找到可以整除k的数,继续循环while(r){len++;//末尾增加1r=r*10+1;//求余r=r%k; }return len;
}
相关文章:

【leetcode 力扣刷题】快乐数/可被k整除的最小整数(可能存在无限循环的技巧题)
可能存在无限循环的技巧题 202. 快乐数数学分析 1015. 可被k整除的最小整数数学分析 202. 快乐数 题目链接:202. 快乐数 题目内容: 理解题意,快乐数就是重复每位数的平方之和得到的新数的过程,最终这个数能变成1。变成1以后&…...

Python 的下一代 HTTP 客户端
迷途小书童 读完需要 9分钟 速读仅需 3 分钟 1 环境 windows 10 64bitpython 3.8httpx 0.23.0 2 简介 之前我们介绍过使用 requests ( https://xugaoxiang.com/2020/11/28/python-module-requests/ ) 来进行 http 操作,本篇介绍另一个功能非常类似的第三方库 httpx&…...
网络安全---webshell实践
一、首先环境配置 1.上传文件并解压 2.进入目录下 为了方便解释,我们只用两个节点,启动之后,大家可以看到有 3 个容器(可想像成有 3 台服务器就成)。 二、使用蚁剑去连接 因为两台节点都在相同的位置存在 ant.jsp&…...

论AI GPT跨境贸易架构及其应用
摘要 2023年初,我司启动了智慧化跨境贸易供应链一体化平台的建设工作。我在该项目中担任系统架构设计师的职务,主要负责设计平台系统架构和安全体系架构。该平台以移动信息化发展为契机,采用”平台+AI”的模式解决现有应用的集中移动化需求。平台整体的逻辑复杂,对系统的高…...

github的CodeSpace如何对外提供TCP 端口服务?
github提供了codespace,一个IDE环境,可以远程以WEB的形式,运行VS code进行开发。 他会给你提供一个虚拟机,4核16G内存,还是很香的,比普通的VPS性能好多了。 缺点是没有独立的IP地址,无法对外进…...

借助Midjourney创作龙九子图
(本文阅读时间:5 分钟) 《西游记》中有这么一段描写: 龙王道:“舍妹有九个儿子。那八个都是好的。第一个小黄龙,见居淮渎;第二个小骊龙,见住济渎;第三个青背龙࿰…...
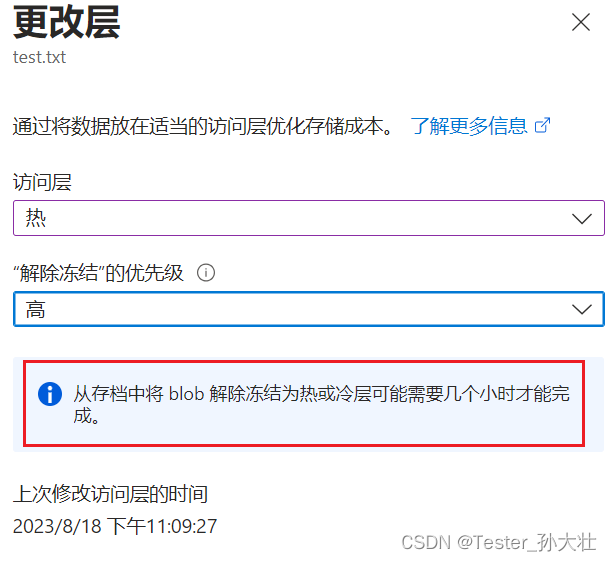
Azure存储访问层
blob数据的热访问层,冷访问层和存档访问层 Azure Blob 存储是一种托管对象存储服务,可用于存储和访问大量非结构化数据,如文本和二进制数据。Azure Blob 存储提供了三个不同层级的访问方式,以适应不同数据的使用模式和成本效益需…...
)
Unity进阶–通过PhotonServer实现人物移动和攻击–PhotonServer(五)
文章目录 Unity进阶–通过PhotonServer实现人物移动和攻击–PhotonServer(五)DLc: 消息类和通信类服务器客户端 Unity进阶–通过PhotonServer实现人物移动和攻击–PhotonServer(五) DLc: 消息类和通信类 Message namespace Net {public class Message{p…...

中间件: Redis安装与部署
单机部署 yum install -y epel-release yum install -y redissed -i "s/bind 127.0.0.1/bind 0.0.0.0/g" /etc/redis.conf sed -i "s/# requirepass foobared/requirepass abcd1234/g" /etc/redis.conf systemctl restart redis集群部署 启动6个redis节点…...
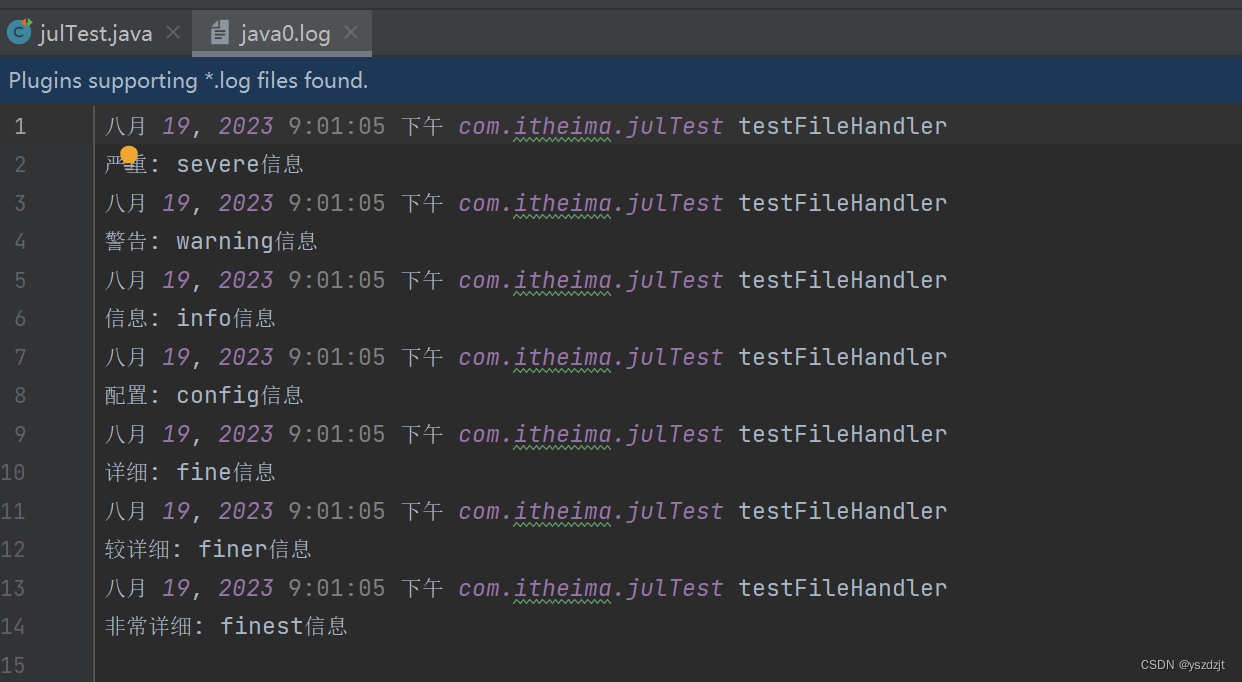
Java日志框架-JUL
JUL全称Java util logging 入门案例 先来看着入门案例,直接创建logger对象,然后传入日志级别和打印的信息,就能在控制台输出信息。 可以看出只输出了部分的信息,其实默认的日志控制器是有一个默认的日志级别的,默认就…...
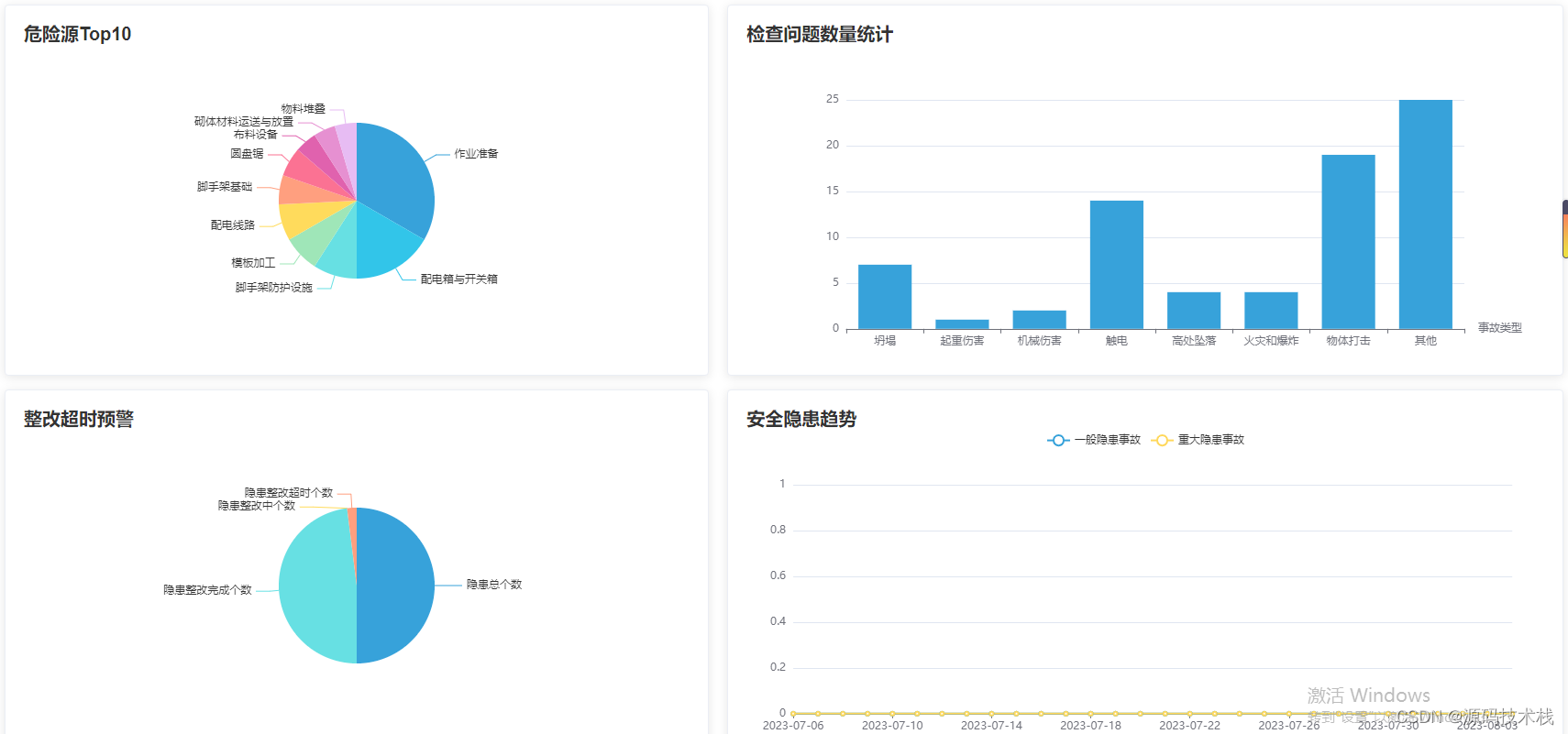
【Java】智慧工地SaaS平台源码:AI/云计算/物联网/智慧监管
智慧工地是指运用信息化手段,围绕施工过程管理,建立互联协同、智能生产、科学管理的施工项目信息化生态圈,并将此数据在虚拟现实环境下与物联网采集到的工程信息进行数据挖掘分析,提供过程趋势预测及专家预案,实现工程…...
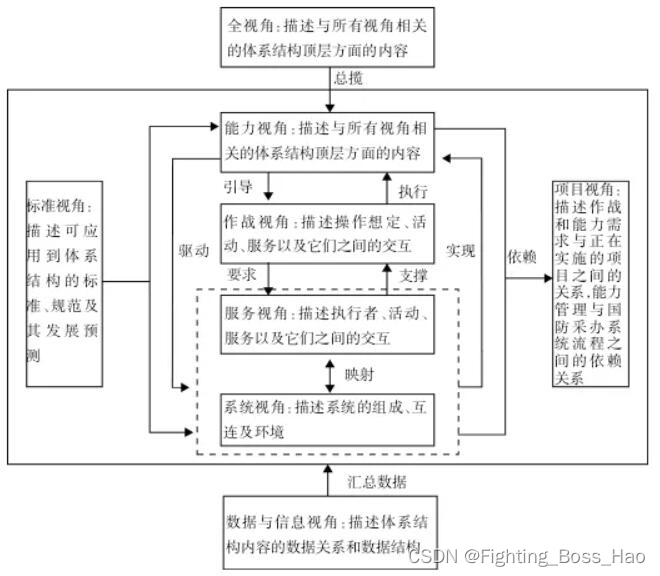
Dodaf架构的学习分享
一.Dodaf的内容 Dodaf的背景 DODAF(Department of Defense Architecture Framework)起源于美国国防部,是一个用于支持复杂系统设计、规划和实施的架构框架。以下是DODAF的背景和起源: 复杂系统需求:在军事和国防领域&…...
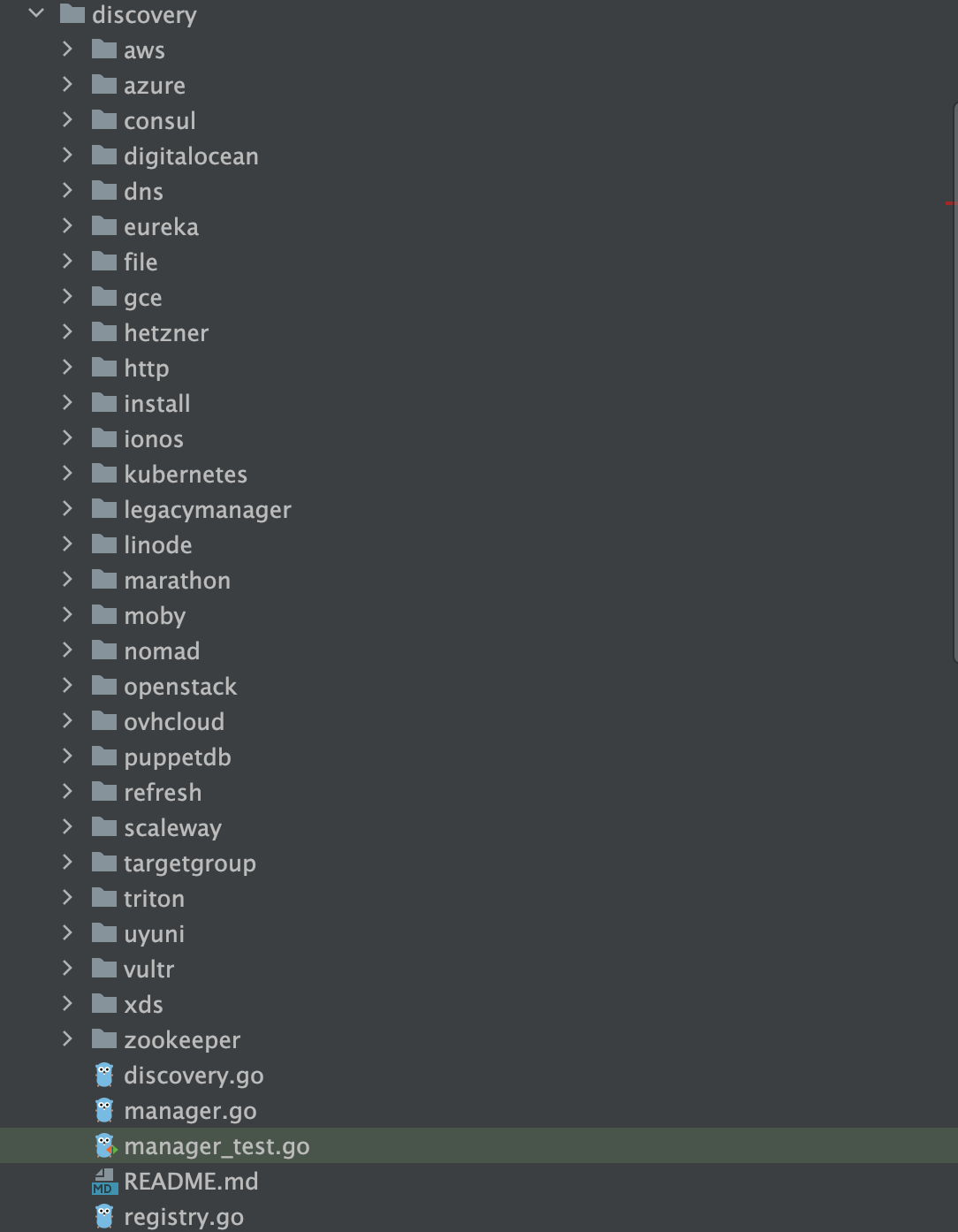
听GPT 讲Prometheus源代码--discovery
Prometheus是一个开源的系统监控和警报工具包,以下是Prometheus源代码中一些主要的文件夹及其作用: cmd/:这个目录包含了Prometheus主要的命令行工具,如prometheus/,promtool/等。每个子目录都代表一个可执行的命令行应…...

HTTP 介绍
HTTP 介绍 HTTP 协议一般指 HTTP(超文本传输协议)。超文本传输协议(英语:HyperText Transfer Protocol,缩写:HTTP)是一种用于分布式、协作式和超媒体信息系统的应用层协议,是因特网…...

Rust语言深入解析:后向和前向链接算法的实现与应用
内容 - 第一部分 (1/3): Rust,作为一个旨在提供安全、并行和高性能的系统编程语言,为开发者带来了独特的编程模式和工具。其中,对于数据结构和算法的实现,Rust提供了一套强大的机制。本文将详细介绍如何在Rust中实现后…...
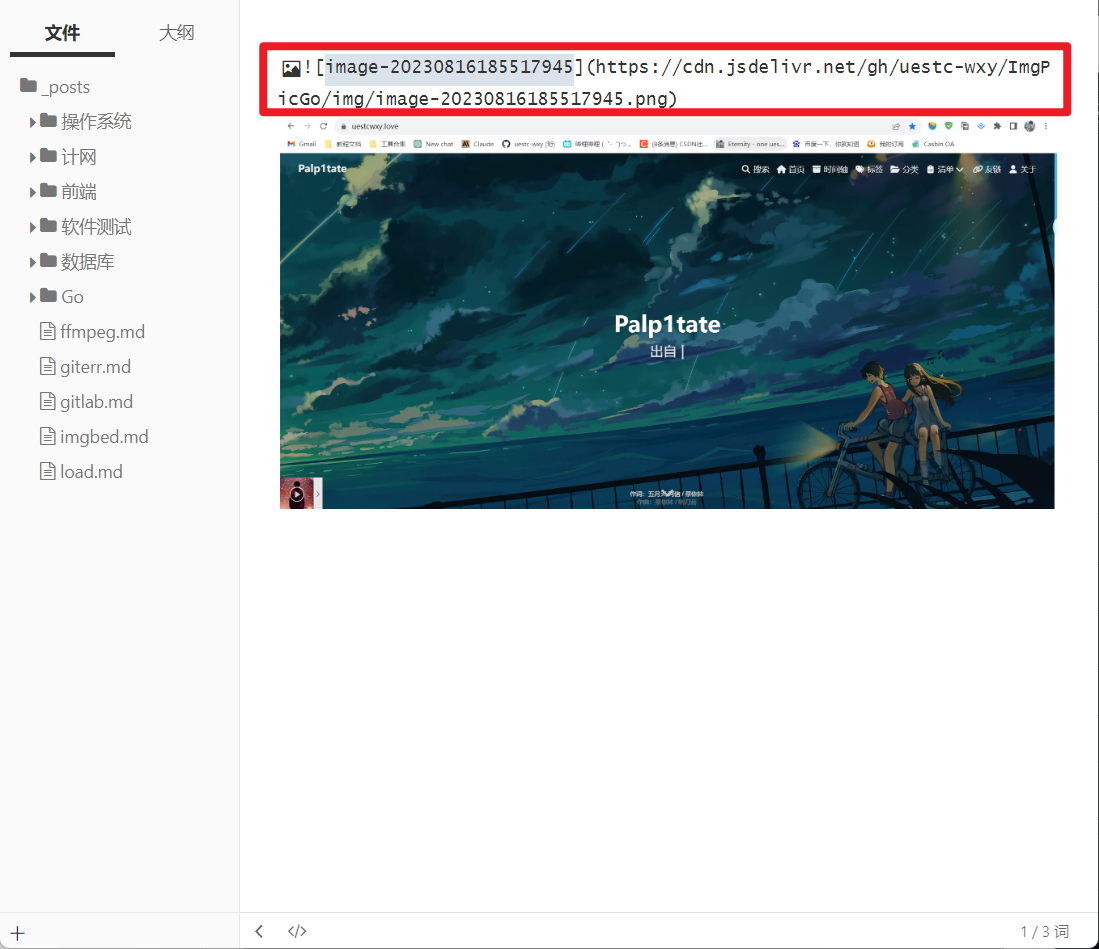
快速提高写作生产力——使用PicGo+Github搭建免费图床,并结合Typora
文章目录 简述PicGo下载PicGo获取Token配置PicGo结合Typora总结 简述PicGo PicGo: 一个用于快速上传图片并获取图片 URL 链接的工具 PicGo 本体支持如下图床: 七牛图床 v1.0腾讯云 COS v4\v5 版本 v1.1 & v1.5.0又拍云 v1.2.0GitHub v1.5.0SM.MS V2 v2.3.0-b…...

Java方法的参数可以有默认值吗?
在日常web开发这种,controller层接受参数时可以通过RequestParam(requiredfalse)设置参数非必填。 所以就想Java的方法可以有非必填这种操作吗?网上搜了一下,发现不支持这种操作。 可以通过方法重载的方式来变相实现。不需要传这个参数就会…...

电子商务的安全防范
(1)安全协议问题:我国大多数尚处在 SSL(安全套接层协议)的应用上,SET 协议的应用还只是刚刚试验成功,在信息的安全保密体制上还不成熟,对安全协议 还没有全球性的标准和规范,相对制约了国际性…...
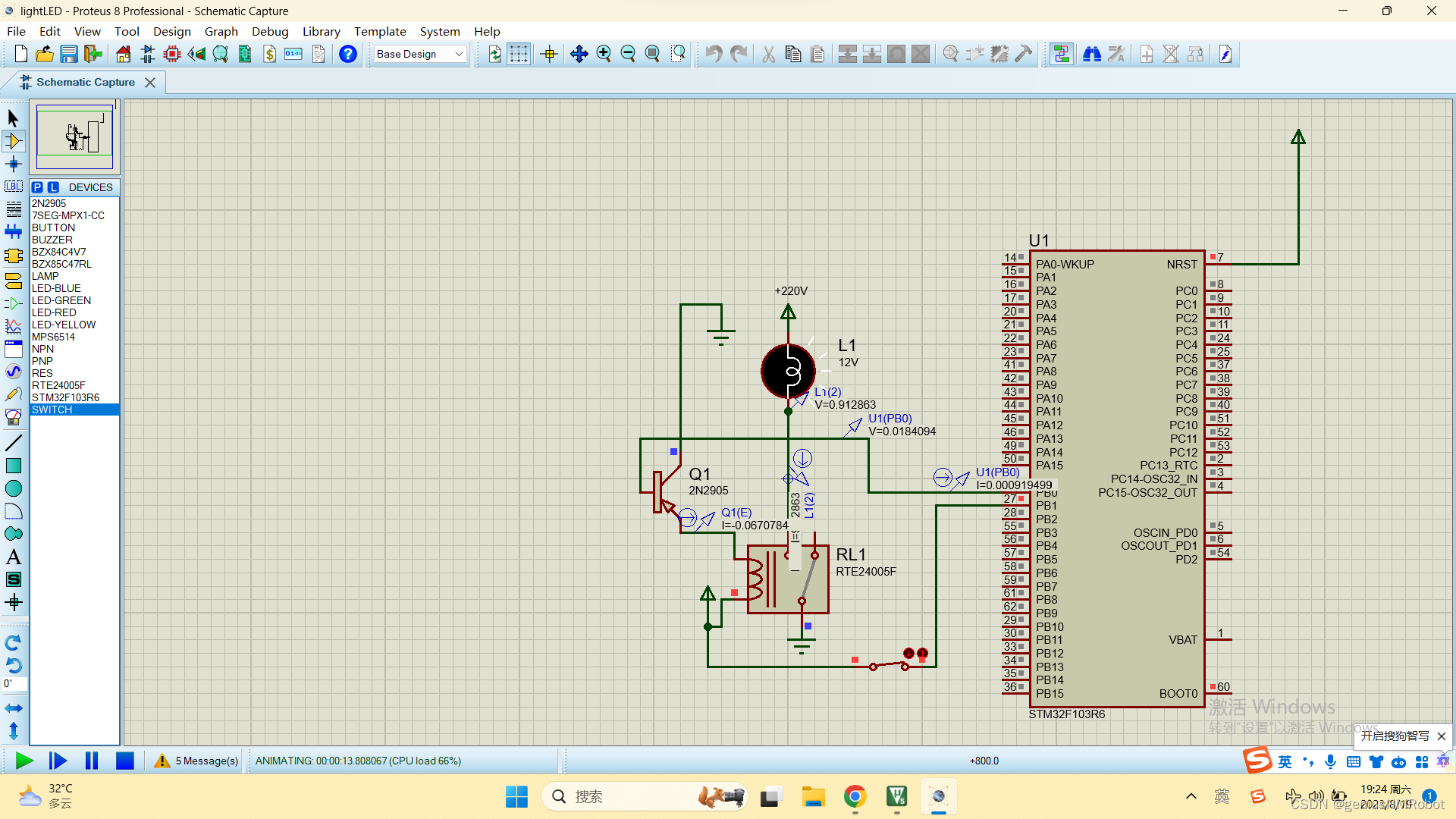
STM32开关输入控制220V灯泡亮灭源代码(附带PROTEUSd电路图)
//main.c文件 /* USER CODE BEGIN Header */ /********************************************************************************* file : main.c* brief : Main program body************************************************************************…...

Spring Boot配置文件
目录 1.配置文件的作用 2.配置文件的格式 3.properties配置文件说明 3.1 properties基本语法 3.2 读取配置文件信息 3.3 properties 缺点分析 4.yml 配置⽂件说明 4.1 yml 基本语法 4.2 yml 使⽤进阶 4.2.1 yml 配置不同数据类型及 null 4.2.2 配置对象 5.propert…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
