数值方法笔记2:解决非线性方程
- 1. 不动点定理及其条件验证
- 2. 收敛阶、收敛检测与收敛加速
- 2.1 如何估计不动点迭代的收敛阶xk+1=g(xk){x}_{{k}+1}={g}\left({x}_{{k}}\right)xk+1=g(xk)
- 2.2 给定精度的情况下,如何预测不动点迭代需要迭代的次数
- 2.3 如何加快收敛的速度
- 2.4 停止不定点迭代的条件
- 2.5 不动点迭代的两个缺点
- 3. 应用:如何求解非线性方程组f(x)=0f(x)=0f(x)=0的解
- 3.1 二分法(Bisection Method of Bolzano)
- 3.2 试位法(False Position Method)
- 3.3 牛顿-拉夫逊方法(Newton-Raphson method)
- 3.4 割线法(Secant Method)
- 3.5 Aitken过程加速
- 3.6 Muller方法(Muller's method)
- 4. 其他问题
- 4.1 如何寻找初值
- 4.2 收敛条件
- 4.3 算法的收敛速度对比
- 4.4 算法的选择
1. 不动点定理及其条件验证
不动点定义:P=g(P){P}={g}({P})P=g(P)
不定点迭代:xk+1=g(xk){x}_{{k}+1}={g}\left({x}_{{k}}\right)xk+1=g(xk)
定理: 如果g(xk)g({x_k})g(xk)是连续的并且序列xk{x_k}xk是收敛的,xk{x_k}xk收敛到方程的解:x=g(x){x}=g({x})x=g(x)
x∗=g(x∗)and xk−>x∗{x}^{*}={g}\left({x}^{*}\right) \text { and } {x}_{{k}}->{x}^{*}x∗=g(x∗) and xk−>x∗

定理: 假设
(1) 对于g(x)g(x)g(x),g′(x)∈C[a,b]g'(x)\in C[a,b]g′(x)∈C[a,b](连续)
(2) KKK是一个正的常数
(3) p0∈(a,b)p_0\in(a,b)p0∈(a,b)
(4) g(x)∈[a,b],∀x∈[a,b]g(x)\in[a,b],\forall x\in[a,b]g(x)∈[a,b],∀x∈[a,b]
那么
(a) 如果∣g′(x)∣≤K<1,∀x∈[a,b],xk+1=g(xk)\left|\mathrm{g}^{\prime}(x)\right| \leq \mathrm{K}<1 , \forall x \in[\mathrm{a}, \mathrm{b}], \mathrm{x}_{\mathrm{k}+1}=\mathrm{g}\left(\mathrm{x}_{\mathrm{k}}\right)∣g′(x)∣≤K<1,∀x∈[a,b],xk+1=g(xk)收敛。
(b) 如果∣g′(x)∣>1,∀x∈[a,b],xk+1=g(xk)\left|\mathrm{g}^{\prime}(x)\right|>1 , \forall x \in[\mathrm{a}, \mathrm{b}], \mathrm{x}_{\mathrm{k}+1}=\mathrm{g}\left(\mathrm{x}_{\mathrm{k}}\right)∣g′(x)∣>1,∀x∈[a,b],xk+1=g(xk)不收敛
曲线的切线斜率k∈(−1,1)k\in(-1,1)k∈(−1,1)看下面的图逐渐收敛:


曲线的切线斜率k∈[−∞,−1)∪(1,∞]k\in[-\infty,-1)\cup (1,\infty]k∈[−∞,−1)∪(1,∞]看下面的图不收敛:


综上所述,不动点迭代满足最重要的是:
(1)∣g′(x)∣≤K<1,∀x∈[a,b]【g′(x)的边界条件】(2)g(x)∈[a,b],∀x∈[a,b],并且有g([a,b])⊂[a,b]【g(x)的边界条件】\begin{aligned}&(1) \left|\mathrm{g}^{\prime}(x)\right| \leq \mathrm{K}<1 ,\forall x \in[\mathrm{a}, \mathrm{b}] & 【g'(x)的边界条件】\\ &(2) \mathrm{g}(x) \in[\mathrm{a}, \mathrm{b}] , \forall x \in[\mathrm{a}, \mathrm{b}] ,并且有g([a, b]) \subset[a, b]& 【g(x)的边界条件】\end{aligned}(1)∣g′(x)∣≤K<1,∀x∈[a,b](2)g(x)∈[a,b],∀x∈[a,b],并且有g([a,b])⊂[a,b]【g′(x)的边界条件】【g(x)的边界条件】
单调和非单调要分别判断边界条件,单调的g(x)的范围看端点就可以了,非单调还要看极值点。

2. 收敛阶、收敛检测与收敛加速
定义;
∣xk+1−x∗∣≤C∣xk−x∗∣p,k>M, for C>0,p>0\left|x_{k+1}-x^{*}\right| \leq C\left|x_{k}-x^{*}\right|^{p}, k>M \text {, for } C>0, p>0∣xk+1−x∗∣≤C∣xk−x∗∣p,k>M, for C>0,p>0
或
limk→∞∣xk+1−x∗∣∣xk−x∗∣p=C\lim _{k \rightarrow \infty} \frac{\left|x_{k+1}-x^{*}\right|}{\left|x_{k}-x^{*}\right|^{p}}=Ck→∞lim∣xk−x∗∣p∣xk+1−x∗∣=C
为ppp阶收敛
其中:
p=1p=1p=1 , 线性收敛(linear convergence)
1<p<21<p<21<p<2 , 超线性收敛(superlinear convergence)
p=2p=2p=2 , 平方收敛(square convergence)
2.1 如何估计不动点迭代的收敛阶xk+1=g(xk){x}_{{k}+1}={g}\left({x}_{{k}}\right)xk+1=g(xk)
定理;设x∗x^*x∗是最优解,如果g′(x∗)=g′′(x∗)=…=g(p−1)(x∗)=0g^{\prime}\left(x^{*}\right)=g^{\prime \prime}\left(x^{*}\right)=\ldots=g^{(p-1)}\left(x^{*}\right)=0g′(x∗)=g′′(x∗)=…=g(p−1)(x∗)=0, g(p)(x∗)≠0g^{(p)}\left(x^{*}\right) \neq 0g(p)(x∗)=0, xk+1=g(xk)x_{k+1}=g\left(x_{k}\right)xk+1=g(xk)是 ppp阶收敛。
证明:
xk+1=g(xk)=g(x∗)+g′(x∗)(xk−x∗)+…+g(p−1)(x∗)(xk−x∗)p−1(p−1)!+g(p)(ξ)(xk−x∗)pp!,【ξ∈[xk,x∗]或[x∗,xk]】⇒xk+1=x∗+g(p)(ξ)(xk−x∗)pp!⇒xk+1−x∗(xk−x∗)p=g(p)(ξ)p!→g(p)(x∗)p!\begin{aligned} x_{k+1}&=g\left(x_{k}\right)=g\left(x^{*}\right)+g^{\prime}\left(x^{*}\right)\left(x_{k}-x^{*}\right)+\ldots\\&+\frac{g^{(p-1)}\left(x^{*}\right)\left(x_{k}-x^{*}\right)^{p-1}}{(p-1) !} +\frac{g^{(p)}(\xi)\left(x_{k}-x^{*}\right)^{p}}{p !}, \quad【\xi \in\left[x_{k}, x^{*}\right] 或\left[x^{*}, x_{k}\right] 】\\ \Rightarrow& x_{k+1}=x^{*}+\frac{g^{(p)}(\xi)\left(x_{k}-x^{*}\right)^{p}}{p !} \\ \Rightarrow& \frac{x_{k+1}-x^{*}}{\left(x_{k}-x^{*}\right)^{p}}=\frac{g^{(p)}(\xi)}{p !} \rightarrow \frac{g^{(p)}\left(x^{*}\right)}{p !} \end{aligned}xk+1⇒⇒=g(xk)=g(x∗)+g′(x∗)(xk−x∗)+…+(p−1)!g(p−1)(x∗)(xk−x∗)p−1+p!g(p)(ξ)(xk−x∗)p,【ξ∈[xk,x∗]或[x∗,xk]】xk+1=x∗+p!g(p)(ξ)(xk−x∗)p(xk−x∗)pxk+1−x∗=p!g(p)(ξ)→p!g(p)(x∗)
2.2 给定精度的情况下,如何预测不动点迭代需要迭代的次数
定义L=maxx∈[a,b]{∣g′(x)∣}<1L=\max _{x \in[a, b]}\left\{\left|g^{\prime}(x)\right|\right\}<1L=maxx∈[a,b]{∣g′(x)∣}<1
迭代的次数满足:k≥ln(ε(1−L)/∣x1−x0∣)/lnLk \geq \ln \left(\varepsilon(1-L) /\left|x_{1}-x_{0}\right|\right) / \ln Lk≥ln(ε(1−L)/∣x1−x0∣)/lnL
证明:
xk+1=g(xk)=g(x∗)+g′(ξ)(xk−x∗)=x∗+g′(ξ)(xk−x∗)⇒∣xk+1−x∗∣≤∣g′(ξ)∥(xk−x∗)∣≤L∣xk−x∗∣≤Lk∣x1−x∗∣\begin{aligned}x_{k+1}=g\left(x_{k}\right)=g\left(x^{*}\right)+g^{\prime}(\xi)\left(x_{k}-x^{*}\right)=x^{*}+g^{\prime}(\xi)\left(x_{k}-x^{*}\right)\\ \Rightarrow \left|x_{k+1}-x^{*}\right| \leq\left|g^{\prime}(\xi) \|\left(x_{k}-x^{*}\right)\right| \leq L\left|x_{k}-x^{*}\right|\le L^{k}\left|x_{1}-x^{*}\right|\end{aligned}xk+1=g(xk)=g(x∗)+g′(ξ)(xk−x∗)=x∗+g′(ξ)(xk−x∗)⇒∣xk+1−x∗∣≤∣g′(ξ)∥(xk−x∗)∣≤L∣xk−x∗∣≤Lk∣x1−x∗∣
又有
∣xk+1−xk∣=∣g(xk)−g(xk−1)∣≤L∣xk−xk−1∣≤Lk∣x1−x0∣\left|x_{k+1}-x_{k}\right|=\left|g\left(x_{k}\right)-g\left(x_{k-1}\right)\right| \leq L\left|x_{k}-x_{k-1}\right| \leq L^{k}\left|x_{1}-x_{0}\right| ∣xk+1−xk∣=∣g(xk)−g(xk−1)∣≤L∣xk−xk−1∣≤Lk∣x1−x0∣
于是有:
∣xk+q−xk∣≤∣xk+q−xk+q−1∣+∣xk+q−1−xk+q−2∣+…+∣xk+1−xk∣≤(Lq−1+Lq−2+…+1)∣xk+1−xk∣<(1+L+L2+…+Lq−1+…)∣xk+1−xk∣=11−L∣xk+1−xk∣≤Lk1−L∣x1−x0∣\begin{aligned} &\left|x_{k+q}-x_{k}\right| \leq\left|x_{k+q}-x_{k+q-1}\right|+\left|x_{k+q-1}-x_{k+q-2}\right|+\ldots+\left|x_{k+1}-x_{k}\right| \\ &\leq\left(L^{q-1}+L^{q-2}+\ldots+1\right)\left|x_{k+1}-x_{k}\right|\\&<\left(1+L+L^{2}+\ldots+L^{q-1}+\ldots\right)\left|x_{k+1}-x_{k}\right|\\ &=\frac{1}{1-L}\left|x_{k+1}-x_{k}\right| \\&\leq \frac{L^{k}}{1-L}\left|x_{1}-x_{0}\right| \end{aligned}∣xk+q−xk∣≤∣xk+q−xk+q−1∣+∣xk+q−1−xk+q−2∣+…+∣xk+1−xk∣≤(Lq−1+Lq−2+…+1)∣xk+1−xk∣<(1+L+L2+…+Lq−1+…)∣xk+1−xk∣=1−L1∣xk+1−xk∣≤1−LLk∣x1−x0∣
让q→∞q \rightarrow \inftyq→∞有
∣x∗−xk∣≤11−L∣xk+1−xk∣≤Lk1−L∣x1−x0∣\left|x^{*}-x_{k}\right| \leq \frac{1}{1-L}\left|x_{k+1}-x_{k}\right| \leq \frac{L^{k}}{1-L}\left|x_{1}-x_{0}\right|∣x∗−xk∣≤1−L1∣xk+1−xk∣≤1−LLk∣x1−x0∣
于是:
Lk1−L∣x1−x0∣≤ε⇒k≥ln(ε(1−L)/∣x1−x0∣)/lnL\frac{L^{k}}{1-L}\left|x_{1}-x_{0}\right| \leq \varepsilon \Rightarrow k \geq \ln \left(\varepsilon(1-L) /\left|x_{1}-x_{0}\right|\right) / \ln L1−LLk∣x1−x0∣≤ε⇒k≥ln(ε(1−L)/∣x1−x0∣)/lnL
2.3 如何加快收敛的速度
xk+1−x∗≈L(xk−x∗)xk+2−x∗≈L(xk+1−x∗)xk+1−x∗xk+2−x∗≈xk−x∗xk+1−x∗⇒x∗≈xk−(xk+1−xk)2xk+2−2xk+1+xk=xΔ\begin{aligned} &x_{k+1}-x^{*} \approx L\left(x_{k}-x^{*}\right) \\ &x_{k+2}-x^{*} \approx L\left(x_{k+1}-x^{*}\right) \\ &\frac{x_{k+1}-x^{*}}{x_{k+2}-x^{*}} \approx \frac{x_{k}-x^{*}}{x_{k+1}-x^{*}} \Rightarrow\quad x^{*} \approx x_{k}-\frac{\left(x_{k+1}-x_{k}\right)^{2}}{x_{k+2}-2 x_{k+1}+x_{k}}=x^{\Delta} \end{aligned}xk+1−x∗≈L(xk−x∗)xk+2−x∗≈L(xk+1−x∗)xk+2−x∗xk+1−x∗≈xk+1−x∗xk−x∗⇒x∗≈xk−xk+2−2xk+1+xk(xk+1−xk)2=xΔ
根据上面的思路我们可以:
Iterationxˉk+1=g(xk)Onemorex^k+1=g(xˉk+1)Tospeedupxk+1=xk−(xˉk+1−xk)2x^k+1−2xˉk+1+xk\begin{aligned}Iteration &\quad \bar{x}_{k+1}=g\left(x_{k}\right) \\ One more &\quad \hat{x}_{k+1}=g\left(\bar{x}_{k+1}\right) \\ To\, speed \,up &\quad x_{k+1}=x_{k}-\frac{\left(\bar{x}_{k+1}-x_{k}\right)^{2}}{\hat{x}_{k+1}-2 \bar{x}_{k+1}+x_{k}} \end{aligned}IterationOnemoreTospeedupxˉk+1=g(xk)x^k+1=g(xˉk+1)xk+1=xk−x^k+1−2xˉk+1+xk(xˉk+1−xk)2
2.4 停止不定点迭代的条件
当L=maxx∈[a,b]{∣g′(x)∣}<1L=\max _{x \in[a, b]}\left\{\left|g^{\prime}(x)\right|\right\}<1L=maxx∈[a,b]{∣g′(x)∣}<1时,可以使用下面的条件:
∣xk+1−xk∣<eps\left|x_{\mathrm{k}+1}-x_{\mathrm{k}}\right|<\mathrm{eps}∣xk+1−xk∣<eps
2.5 不动点迭代的两个缺点
- 很难估计L(maxx∈[a,b]{∣g′(x)∣})L(\max _{x \in[a, b]}\left\{\left|g^{\prime}(x)\right|\right\})L(maxx∈[a,b]{∣g′(x)∣})
- L<1L<1L<1时无法收敛。
3. 应用:如何求解非线性方程组f(x)=0f(x)=0f(x)=0的解

3.1 二分法(Bisection Method of Bolzano)
算法的流程:
- 用一个区间找到一个根。
- 用中点分割该区间。
- 选择其中的一个子区间作为新的位置。

a=x0,b=x0+hc=a+b2f(a)f(b)<0,\begin{aligned} &a=x_{0}, \quad b=x_{0}+h \\ &c=\frac{a+b}{2}\\ &f(a) f(b)<0, \end{aligned}a=x0,b=x0+hc=2a+bf(a)f(b)<0,
于是:

[a,b]→[a1,b1]→[a2,b2]→…→[an,bn]a=a0≤a1≤⋯≤an≤⋯≤r≤⋯≤bn≤⋯≤b1≤b0=b\begin{aligned} &{[{a}, {b}]\rightarrow\left[{a}_{1}, {~b}_{1}\right]\rightarrow \left[{a}_{2}, {~b}_{2}\right]\rightarrow\ldots\rightarrow\left[{a}_{{n}}, {b}_{{n}}\right]} \\ &a=a_{0} \leq a_{1} \leq \cdots \leq a_{n} \leq \cdots \leq r \leq \cdots \leq b_{n} \leq \cdots \leq b_{1} \leq b_{0}=b \end{aligned}[a,b]→[a1, b1]→[a2, b2]→…→[an,bn]a=a0≤a1≤⋯≤an≤⋯≤r≤⋯≤bn≤⋯≤b1≤b0=b
定义rrr是精确解。
∣r−cn∣≤b−a2n+1,for n=0,1,2,…cn=an+bn2\begin{aligned} &\left|r-c_{n}\right| \leq \frac{b-a}{2^{n+1}}, \text { for } n=0,1,2, \ldots \\ &c_{n}=\frac{a_{n}+b_{n}}{2} \end{aligned}∣r−cn∣≤2n+1b−a, for n=0,1,2,…cn=2an+bn
迭代次数N:
∣r−cn∣≤b−a2n+1<δ2n+1>b−aδ(n+1)ln2>ln(b−a)−lnδn+1>ln(b−a)−lnδln2N=int(ln(b−a)−lnδln2)\begin{aligned} &\left|r-c_{n}\right| \leq \frac{b-a}{2^{n+1}}<\delta \\ &2^{n+1}>\frac{b-a}{\delta} \\ &(n+1) \ln 2>\ln (b-a)-\ln \delta \\ &n+1>\frac{\ln (b-a)-\ln \delta}{\ln 2} \\ &N=\operatorname{int}\left(\frac{\ln (b-a)-\ln \delta}{\ln 2}\right) \end{aligned}∣r−cn∣≤2n+1b−a<δ2n+1>δb−a(n+1)ln2>ln(b−a)−lnδn+1>ln2ln(b−a)−lnδN=int(ln2ln(b−a)−lnδ)
简单地利用二分法可以判断区间内有没有零点(区间内有变号【可取最大值和最小值】)
3.2 试位法(False Position Method)
算法的流程:
- 用一个区间找到一个根。
- 以割线与X轴的交点划分区间。(过程中仍然保证端点的异号,让区间包含零点)
- 选择其中一个子区间作为新的位置。
c=b−f(b)(b−a)f(b)−f(a)c1→c2→…→r[an,bn]→[a,c]:=[an+1,bn+1]c=b-\frac{f(b)(b-a)}{f(b)-f(a)}\\ c_{1}\rightarrow c_{2}\rightarrow \ldots\rightarrow r\\ \left[a_{n}, b_{n}\right]\rightarrow [a, c]:=\left[a_{n+1}, b_{n+1}\right]c=b−f(b)−f(a)f(b)(b−a)c1→c2→…→r[an,bn]→[a,c]:=[an+1,bn+1]

缺点:在凹函数下不适用,不会收敛。
3.3 牛顿-拉夫逊方法(Newton-Raphson method)
我们知道不动点迭代,能不能用到求解非线性方程组呢?
使用泰勒展式:
f(xk+1)=f(xk)+f′(xk)(xk+1−xk)+O(∣d∣2)=0f(x_{k+1})=f\left(x_{{k}}\right)+f^{\prime}\left(x_{{k}}\right) (x_{k+1}-x_k)+{O}\left(|d|^{2}\right)=0f(xk+1)=f(xk)+f′(xk)(xk+1−xk)+O(∣d∣2)=0
于是我们可以让
f(xk)+f′(xk)(xk+1−xk)=0f\left(x_{\mathrm{k}}\right)+f^{\prime}\left(x_{\mathrm{k}}\right)\left(x_{{k}+1}-x_{{k}}\right)=0f(xk)+f′(xk)(xk+1−xk)=0
使得:
xk+1=xk−f(xk)/f′(xk)=g(xk)x_{\mathrm{k}+1}=x_{{k}}-f\left(x_{\mathrm{k}}\right) / f^{\prime}\left(x_{\mathrm{k}}\right)=g(x_k)xk+1=xk−f(xk)/f′(xk)=g(xk)
总结Newton-Raphson方法即:
f(x)=0x=g(x)=x−f(x)f′(x)xk+1=g(xk)=xk−f(xk)f′(xk)\begin{array}{l} f(x)=0 \\ x=g(x)=x-\frac{f(x)}{f^{\prime}(x)} \\ x_{k+1}=g\left(x_{k}\right)=x_{k}-\frac{f\left(x_{k}\right)}{f^{\prime}\left(x_{k}\right)} \end{array}f(x)=0x=g(x)=x−f′(x)f(x)xk+1=g(xk)=xk−f′(xk)f(xk)

我们可以证明在解的附近,Newton-Raphson方法是收敛的。
证明:
g(x)=x−f(x)/f′(x)g(x)=x-f(x) / f^{\prime}(x)g(x)=x−f(x)/f′(x)
g′(x)=1−f′(x)f′(x)−f(x)f′′(x)[f′(x)]2=f(x)f′′(x)[f′(x)]2g^{\prime}(x)=1-\frac{f^{\prime}(x) f^{\prime}(x)-f(x) f^{\prime \prime}(x)}{\left[f^{\prime}(x)\right]^{2}}=\frac{f(x) f^{\prime \prime}(x)}{\left[f^{\prime}(x)\right]^{2}}g′(x)=1−[f′(x)]2f′(x)f′(x)−f(x)f′′(x)=[f′(x)]2f(x)f′′(x)
我们知道不动点的条件是∣g′(x)∣<K<1\left|g^{\prime}(x)\right|<K<1∣g′(x)∣<K<1,当我们取的邻域足够小,条件g([a,b])⊂[a,b]g([a, b]) \subset[a, b]g([a,b])⊂[a,b]会满足,注意到f(x∗)=0f(x^*)=0f(x∗)=0,在解的邻域附近,因为f(x)=0f(x)=0f(x)=0,所以g′(x)=0g'(x)=0g′(x)=0。
各种条件下的推导(不做要求,想了解可以看一下)
- f′(x∗)>0and f′′(x∗)<0,g([x∗−δ,x∗+δ])⊂[x∗−δ,x∗+δ]f^{\prime}\left(x^{*}\right)>0 \text { and } f^{\prime \prime}\left(x^{*}\right)<0, \,\,\,\,g\left(\left[x^{*}-\delta, x^{*}+\delta\right]\right) \subset\left[x^{*}-\delta, x^{*}+\delta\right]f′(x∗)>0 and f′′(x∗)<0,g([x∗−δ,x∗+δ])⊂[x∗−δ,x∗+δ]
x∗−δ<g(x∗−δ)=(x∗−δ)−f(x∗−δ)f′(x∗−δ)⇔0<−f(x∗−δ)f′(x∗−δ)⇔f(x∗−δ)f′(x∗−δ)<0⇔f(x∗−δ)<0⇔f(x∗)−f′(ξ)δ<0【ξ∈[x∗−δ,x∗]】⇔−f′(ξ)δ<0⇒∃δ1>0,f′(ξ)>0,for x∗−ξ<δ1\begin{aligned} &x^{*}-\delta<g\left(x^{*}-\delta\right)=\left(x^{*}-\delta\right)-\frac{f\left(x^{*}-\delta\right)}{f^{\prime}\left(x^{*}-\delta\right)} \\ \Leftrightarrow& 0<-\frac{f\left(x^{*}-\delta\right)}{f^{\prime}\left(x^{*}-\delta\right)} \\ \Leftrightarrow &\frac{f\left(x^{*}-\delta\right)}{f^{\prime}\left(x^{*}-\delta\right)}<0 \\ \Leftrightarrow &f\left(x^{*}-\delta\right)<0 \\ \Leftrightarrow &f\left(x^{*}\right)-f^{\prime}(\xi) \delta<0 【\xi\in[x^*-\delta,x^*]】\\ \Leftrightarrow&-f^{\prime}(\xi) \delta<0\\ \Rightarrow&\exists \delta_1>0, f^{\prime}(\xi)>0, \text { for } x^{*}-\xi<\delta_1 \\ \end{aligned}⇔⇔⇔⇔⇔⇒x∗−δ<g(x∗−δ)=(x∗−δ)−f′(x∗−δ)f(x∗−δ)0<−f′(x∗−δ)f(x∗−δ)f′(x∗−δ)f(x∗−δ)<0f(x∗−δ)<0f(x∗)−f′(ξ)δ<0【ξ∈[x∗−δ,x∗]】−f′(ξ)δ<0∃δ1>0,f′(ξ)>0, for x∗−ξ<δ1
又有
f′′(x∗)<0⇒∃δ2>0,f′′(x)<0【保号性】⇒g′(x)=f(x)f′′(x)[f′(x)]2>0,for x∗−x<δ2【δ2足够小,导数保号性,f′(x)>0,x<x∗,f(x∗)=0,f(x)<0】\begin{aligned} &f^{\prime \prime}\left(x^{*}\right)<0\\ \Rightarrow & \exists \delta_2>0, f^{\prime \prime}(x)<0 【保号性】\\ \Rightarrow & g^{\prime}(x)=\frac{f(x) f^{\prime \prime}(x)}{\left[f^{\prime}(x)\right]^{2}}>0, \text { for } x^{*}-x<\delta_2\\ &【\delta_2足够小,导数保号性,f'(x)>0,x<x^*,f(x^*)=0,f(x)<0】 \end{aligned}⇒⇒f′′(x∗)<0∃δ2>0,f′′(x)<0【保号性】g′(x)=[f′(x)]2f(x)f′′(x)>0, for x∗−x<δ2【δ2足够小,导数保号性,f′(x)>0,x<x∗,f(x∗)=0,f(x)<0】
当δ<min{δ1,δ2}\delta<\min\{\delta_1,\delta_2\}δ<min{δ1,δ2}有:
x∗−δ<g(x∗−δ)<g(x),for x∗−x<δx^{*}-\delta<g\left(x^{*}-\delta\right)<g(x), \text { for } x^{*}-x<\deltax∗−δ<g(x∗−δ)<g(x), for x∗−x<δ- f′(x∗)>0and f′′(x∗)<0,g([x∗−δ,x∗+δ])⊂[x∗−δ,x∗+δ]f^{\prime}\left(x^{*}\right)>0 \text { and } f^{\prime \prime}\left(x^{*}\right)<0, \,\,\,\,g\left(\left[x^{*}-\delta, x^{*}+\delta\right]\right) \subset\left[x^{*}-\delta, x^{*}+\delta\right]f′(x∗)>0 and f′′(x∗)<0,g([x∗−δ,x∗+δ])⊂[x∗−δ,x∗+δ]
x∗−δ<g(x∗−δ)=(x∗−δ)−f(x∗−δ)f′(x∗−δ)⇔0<−f(x∗−δ)f′(x∗−δ)⇔f(x∗−δ)f′(x∗−δ)<0⇔f(x∗−δ)<0⇔f(x∗)−f′(ξ)δ<0【ξ∈[x∗−δ,x∗]】⇔−f′(ξ)δ<0⇒∃δ1>0,f′(ξ)>0,for x∗−ξ<δ1\begin{aligned} &x^{*}-\delta<g\left(x^{*}-\delta\right)=\left(x^{*}-\delta\right)-\frac{f\left(x^{*}-\delta\right)}{f^{\prime}\left(x^{*}-\delta\right)} \\ \Leftrightarrow& 0<-\frac{f\left(x^{*}-\delta\right)}{f^{\prime}\left(x^{*}-\delta\right)} \\ \Leftrightarrow &\frac{f\left(x^{*}-\delta\right)}{f^{\prime}\left(x^{*}-\delta\right)}<0 \\ \Leftrightarrow &f\left(x^{*}-\delta\right)<0 \\ \Leftrightarrow &f\left(x^{*}\right)-f^{\prime}(\xi) \delta<0 【\xi\in[x^*-\delta,x^*]】\\ \Leftrightarrow&-f^{\prime}(\xi) \delta<0\\ \Rightarrow&\exists \delta_1>0, f^{\prime}(\xi)>0, \text { for } x^{*}-\xi<\delta_1 \\ \end{aligned}⇔⇔⇔⇔⇔⇒x∗−δ<g(x∗−δ)=(x∗−δ)−f′(x∗−δ)f(x∗−δ)0<−f′(x∗−δ)f(x∗−δ)f′(x∗−δ)f(x∗−δ)<0f(x∗−δ)<0f(x∗)−f′(ξ)δ<0【ξ∈[x∗−δ,x∗]】−f′(ξ)δ<0∃δ1>0,f′(ξ)>0, for x∗−ξ<δ1
又有
f′′(x∗)>0⇒∃δ2>0,f′′(x)<0【保号性】⇒g′(x)=f(x)f′′(x)[f′(x)]2<0,for x∗−x<δ2【δ2足够小,导数保号性,f′(x)>0,x<x∗,f(x∗)=0,f(x)<0】\begin{aligned} &f^{\prime \prime}\left(x^{*}\right)>0\\ \Rightarrow & \exists \delta_2>0, f^{\prime \prime}(x)<0 【保号性】\\ \Rightarrow & g^{\prime}(x)=\frac{f(x) f^{\prime \prime}(x)}{\left[f^{\prime}(x)\right]^{2}}<0, \text { for } x^{*}-x<\delta_2\\ &【\delta_2足够小,导数保号性,f'(x)>0,x<x^*,f(x^*)=0,f(x)<0】 \end{aligned}⇒⇒f′′(x∗)>0∃δ2>0,f′′(x)<0【保号性】g′(x)=[f′(x)]2f(x)f′′(x)<0, for x∗−x<δ2【δ2足够小,导数保号性,f′(x)>0,x<x∗,f(x∗)=0,f(x)<0】
当δ<min{δ1,δ2}\delta<\min\{\delta_1,\delta_2\}δ<min{δ1,δ2}有:
x∗−δ<x∗=g(x∗)<g(x),for x∗−x<δ,x<x∗x^{*}-\delta<x^{*}=g\left(x^{*}\right)<g(x), \text { for } x^{*}-x<\delta,x<x^*x∗−δ<x∗=g(x∗)<g(x), for x∗−x<δ,x<x∗
注意Newton-Raphson方法对于单根是二阶收敛(二次收敛)【quadratic convergence】
∣En+1∣≈∣f′′(p)∣2∣f′(p)∣∣En∣2n→∞\left|E_{n+1}\right| \approx \frac{\left|f^{\prime \prime}(p)\right|}{2\left|f^{\prime}(p)\right|}\left|E_{n}\right|^{2}\quad n\rightarrow \infty∣En+1∣≈2∣f′(p)∣∣f′′(p)∣∣En∣2n→∞
证明:
而对于多重根是线性(一次)收敛,收敛速度降低。
∣En+1∣≈M−1M∣En∣n→∞\left|E_{n+1}\right| \approx \frac{M-1}{M}\left|E_{n}\right |\quad n\rightarrow \infty∣En+1∣≈MM−1∣En∣n→∞
证明:
如果出现了多重根p∗p^*p∗,我们看到在f′(p∗)=0f'(p^*)=0f′(p∗)=0,Newton-Raphson方法的分母会出现0.然而一般来说,分子f(pk)f(p_k)f(pk)要比分母f′(pk)f'(p_k)f′(pk)先出现0,所以Newton-Raphson方法一般还是可以用的。
Newton-Raphson方法的问题:
1.分母可能为0,除以零是不允许的。
2.收敛到一个不同的根,或发散。
3.产生一个循环序列。
4.产生一个发散的振荡序列。

由于多重根线性收敛的问题,可以考虑Newton-Raphson方法加速:
pk=pk−1−Mf(pk−1)f′(pk−1)M>1p_{k}=p_{k-1}-\frac{M f\left(p_{k-1}\right)}{f^{\prime}\left(p_{k-1}\right)}\quad M>1pk=pk−1−f′(pk−1)Mf(pk−1)M>1
证明:
3.4 割线法(Secant Method)

当Newton-Raphson的导数不好显式表达的时候,可以通过两端点的直线的斜率来近似导数。
我们有:
xk+2=g(xk,xk+1)=xk+1−f(xk+1)(xk+1−xk)f(xk+1)−f(xk)x_{k+2}=g\left(x_{k}, x_{k+1}\right)=x_{k+1}-\frac{f\left(x_{k+1}\right)\left(x_{k+1}-x_{k}\right)}{f\left(x_{k+1}\right)-f\left(x_{k}\right)}xk+2=g(xk,xk+1)=xk+1−f(xk+1)−f(xk)f(xk+1)(xk+1−xk)
3.5 Aitken过程加速
使用不定点的迭代,Aitken过程加速又称为史蒂芬森加速(Steffensen’s acceleration).注意,只对一阶方法有效。
limn→∞p−pn+1p−pn=A,p≈pn+2pn−pn+12pn+2−2pn+1+pn=qn\lim _{n \rightarrow \infty} \frac{p-p_{n+1}}{p-p_{n}}=A, \quad p \approx \frac{p_{n+2} p_{n}-p_{n+1}^{2}}{p_{n+2}-2 p_{n+1}+p_{n}}=q_{n}n→∞limp−pnp−pn+1=A,p≈pn+2−2pn+1+pnpn+2pn−pn+12=qn
3.6 Muller方法(Muller’s method)

给定三个初始值(p0,f(p0)),(p1,f(p1)),(p2,f(p2))\left(p_{0}, f\left(p_{0}\right)\right),\left(p_{1}, f\left(p_{1}\right)\right),\left(p_{2},f\left(p_{2}\right)\right)(p0,f(p0)),(p1,f(p1)),(p2,f(p2))
令
t=x−p2h0=p0−p2,h1=p1−p2\begin{aligned} &t=x-p_{2} \\ &h_{0}=p_{0}-p_{2}, h_{1}=p_{1}-p_{2} \\ \end{aligned}t=x−p2h0=p0−p2,h1=p1−p2
我们使用二次函数计算下一个点:
y=at2+bt+cy=a t^{2}+b t+cy=at2+bt+c
则有:
t=h0:ah02+bh0+c=f0⇒ah02+bh0=f0−c=e0t=h1:ah12+bh1+c=f1⇒ah12+bh1=f1−c=e1t=0:a02+b0+c=f2⇒c=f2\begin{aligned} t=h_{0}: a h_{0}^{2}+b h_{0}+c=f_{0} &\Rightarrow a h_{0}^{2}+b h_{0}=f_{0}-c=e_{0} \\ t=h_{1}: a h_{1}^{2}+b h_{1}+c=f_{1} &\Rightarrow a h_{1}^{2}+b h_{1}=f_{1}-c=e_{1} \\ t=0: a 0^{2}+b 0+c=f_{2}& \Rightarrow c=f_{2} \end{aligned}t=h0:ah02+bh0+c=f0t=h1:ah12+bh1+c=f1t=0:a02+b0+c=f2⇒ah02+bh0=f0−c=e0⇒ah12+bh1=f1−c=e1⇒c=f2
解得:
a=e0h1−e1h0h1h02−h0h12,b=e1h02−e0h12h1h02−h0h12a=\frac{e_{0} h_{1}-e_{1} h_{0}}{h_{1} h_{0}^{2}-h_{0} h_{1}^{2}}, \quad b=\frac{e_{1} h_{0}^{2}-e_{0} h_{1}^{2}}{h_{1} h_{0}^{2}-h_{0} h_{1}^{2}}a=h1h02−h0h12e0h1−e1h0,b=h1h02−h0h12e1h02−e0h12
于是得到:
at2+bt+c=0:t=z1,z2⇒zi=−2cb±b2−4acz=argmin{∣zi∣}【对于一个复数,在计算中只保留其实数部分】\begin{aligned} &a t^{2}+b t+c=0: \quad t=z_{1}, z_{2} \Rightarrow z_{i}=\frac{-2 c}{b \pm \sqrt{b^{2}-4 a c}} \\ &z=\arg \min \left\{\left|z_{i}\right|\right\}【\text{对于一个复数,在计算中只保留其实数部分}】 \end{aligned}at2+bt+c=0:t=z1,z2⇒zi=b±b2−4ac−2cz=argmin{∣zi∣}【对于一个复数,在计算中只保留其实数部分】
p3=p2+zp_{3}=p_{2}+zp3=p2+z
继续得到(pˉ1,pˉ2,p3)\left(\bar{p}_{1}, \bar{p}_{2}, p_{3}\right)(pˉ1,pˉ2,p3),其中pˉ1,pˉ2\bar{p}_{1}, \bar{p}_{2}pˉ1,pˉ2是距离p3p_3p3最近的两个点。
4. 其他问题
4.1 如何寻找初值
例如

可以有两个判断条件:
-
【针对r1r_1r1和r2r_2r2】
f(xk−1)f(xk)<0[a,b]=[xk−1,xk]f\left(x_{k-1}\right) f\left(x_{k}\right)<0 \quad[{a}, {b}]=\left[{x}_{{k}-1}, {x}_{{k}}\right]f(xk−1)f(xk)<0[a,b]=[xk−1,xk] -
【针对r3r_3r3】
∣f(xk)∣<ε并且(f(xk)−f(xk−1))(f(xk+1)−f(xk))<0[a,b]=[xk−1,xk+1]\left|f\left(x_{k}\right)\right|<\varepsilon \text { 并且}\left(f\left(x_{k}\right)-f\left(x_{k-1}\right)\right) \left(f\left(x_{k+1}\right)-f\left(x_{k}\right)\right)<0\quad [{a}, {b}]=\left[{x}_{{k}-1}, {x}_{{k}+1}\right]∣f(xk)∣<ε 并且(f(xk)−f(xk−1))(f(xk+1)−f(xk))<0[a,b]=[xk−1,xk+1]
4.2 收敛条件
可以有两个收敛条件:
1. 根据纵坐标
∣f(xk)∣<ε\left|f\left(x_{k}\right)\right|<\varepsilon∣f(xk)∣<ε

误差为:Errorx=∣xk−r∣\text{Error}_{x}=\left|x_{k}-r\right|Errorx=∣xk−r∣
2. 根据横坐标
∣xk−xk−1∣<δ\left|x_{k}-x_{k-1}\right|<\delta∣xk−xk−1∣<δ
由以下推出:
∣xk−r∣<δ⇒∣xk−xk−1∣<δ\left|x_{k}-r\right|<\delta \Rightarrow\left|x_{k}-x_{k-1}\right|<\delta∣xk−r∣<δ⇒∣xk−xk−1∣<δ

误差为:Error f=max{∣f(r−δ)∣,∣f(r+δ)∣}\text { Error }_{f}=\max \{|f(r-\delta)|,|f(r+\delta)|\} Error f=max{∣f(r−δ)∣,∣f(r+δ)∣}
3. 我们也可以把上面两个进行组合:
∣f(xk)∣<ε并且∣xk−r∣<δ\left|f\left(x_{k}\right)\right|<\varepsilon \text{并且}\left|x_{k}-r\right|<\delta∣f(xk)∣<ε并且∣xk−r∣<δ

- 如果针对Newton-Raphson问题,我们还可以有如下的判断标准:
①f′(r)≠0f^{\prime}(r) \neq 0f′(r)=0
②x0∈[r−δ,r+δ]x_{0} \in[r-\delta, r+\delta]x0∈[r−δ,r+δ], δ\deltaδ足够小。
4.3 算法的收敛速度对比

4.4 算法的选择
单根:
Newton-Raphson方法
双根(当分母为0失效):
Newton-Raphson方法
Steffensen’s method
相关文章:

数值方法笔记2:解决非线性方程
1. 不动点定理及其条件验证2. 收敛阶、收敛检测与收敛加速2.1 如何估计不动点迭代的收敛阶xk1g(xk){x}_{{k}1}{g}\left({x}_{{k}}\right)xk1g(xk)2.2 给定精度的情况下,如何预测不动点迭代需要迭代的次数2.3 如何加快收敛的速度2.4 停止不定点迭代的条件2.5 不动…...

基于SpringBoot的在线文档管理系统
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...

软件体系结构(期末复习)
文章目录软件体系结构软件体系结构概论软件体系结构建模软件体系结构风格统一建模语言基于体系结构的软件开发软件体系结构 软件体系结构概论 软件危机是指计算机软件的开发和维护过程中遇到的一系列严重问题。 软件危机的表现: 软件危机的原因: 软件工程的基本要素…...

[vue3] pinia的基本使用
使用Pinia npm install piniastore文件里index.js import { createPinia } from piniaconst pinia createPinia()export default piniamain.js导入并引用 import { createApp } from vue import App from ./App.vue import pinia from ./storescreateApp(App).use(pinia).m…...

进程和线程详解
在计算机领域中,进程和线程是非常重要的概念。了解进程和线程是软件开发的基础,也是计算机科学教育中的一部分。本文将介绍进程和线程的概念、区别和应用。 一、什么是进程 在计算机科学中,进程是正在执行的程序实例。一个进程可以由一个或…...
《刀锋》读书笔记
刀锋(毛姆长篇作品精选)毛姆50个笔记点评认为好看的确是完美的结局。《刀锋》里面的人每个人都以自己的方式生活着。艾略特的势利,拉里的自由,伊莎贝尔的现实,苏珊的清醒,索菲的堕落,至于“我”…...

nginx中的ngx_modules
ngx_modules和ngx_module_names是configure脚本生成的,是在objs/ngx_modules.c文件中与其生成的相关的脚本文件相关的变量在options脚本中定义了objs目录的变量NGX_OBJSobjs在init脚本中定义的最终存放ngx_modules的文件 NGX_MODULES_C$NGX_OBJS/ngx_modules.c2. 处…...

设计模式之访问者模式
什么是访问者模式 访问者模式提供了一个作用于某对象结构中的各元素的操作表示,他使我们可以在不改变各元素的类的前提下定义作用于这些元素的新操作。 访问者模式主要包含以下几个角色: Vistor(抽象访问者):为对象结…...
Go项目(三)
文章目录用户微服务表结构查表web 服务跨域问题图形验证码短信用户注册服务中心注册 grpc 服务动态获取端口负载均衡配置中心启动项目小结用户微服务 作为系统的第一个微服务,开发的技术点前面已经了解了一遍,虽有待补充,但急需实战这里主要…...

CTK学习:(一)编译CTK
CTK插件框架简介 CTK Plugin Framework是用于C++的动态组件系统,以OSGi规范为模型。在此框架下,应用程序由不同的组件组成,遵循面向服务的方法。 ctk是一个开源项目,Github 地址:https://github.com/commontk。 源码地址commontk/CTK: A set of common support code for…...

15种NLP数据增强方法总结与对比
数据增强的方法 数据增强(Data Augmentation,简称DA),是指根据现有数据,合成新数据的一类方法。毕竟数据才是真正的效果天花板,有了更多数据后可以提升效果、增强模型泛化能力、提高鲁棒性等。然而由于NLP…...

Python每日一练(20230219)
目录 1. 循环随机取数组直到得出指定数字? 2. 旋转链表 3. 区间和的个数 1. 循环随机取数组直到得出指定数字? 举个例子: 随机数字范围:0~100 每组数字量:6(s1,s2,s3,s4,s5,s6) 第二轮开始随…...

vTESTstudio - VT System CAPL Functions - VT7001
vtsSerialClose - 关闭VT系统通道的串行端口功能:关闭由系统变量命名空间指定的VT系统通道的串行端口。Target:目标通道变量空间名称,例如:VTS::ECUPowerSupply返回值:0:成功重置目标通道最大和最小值-1&am…...
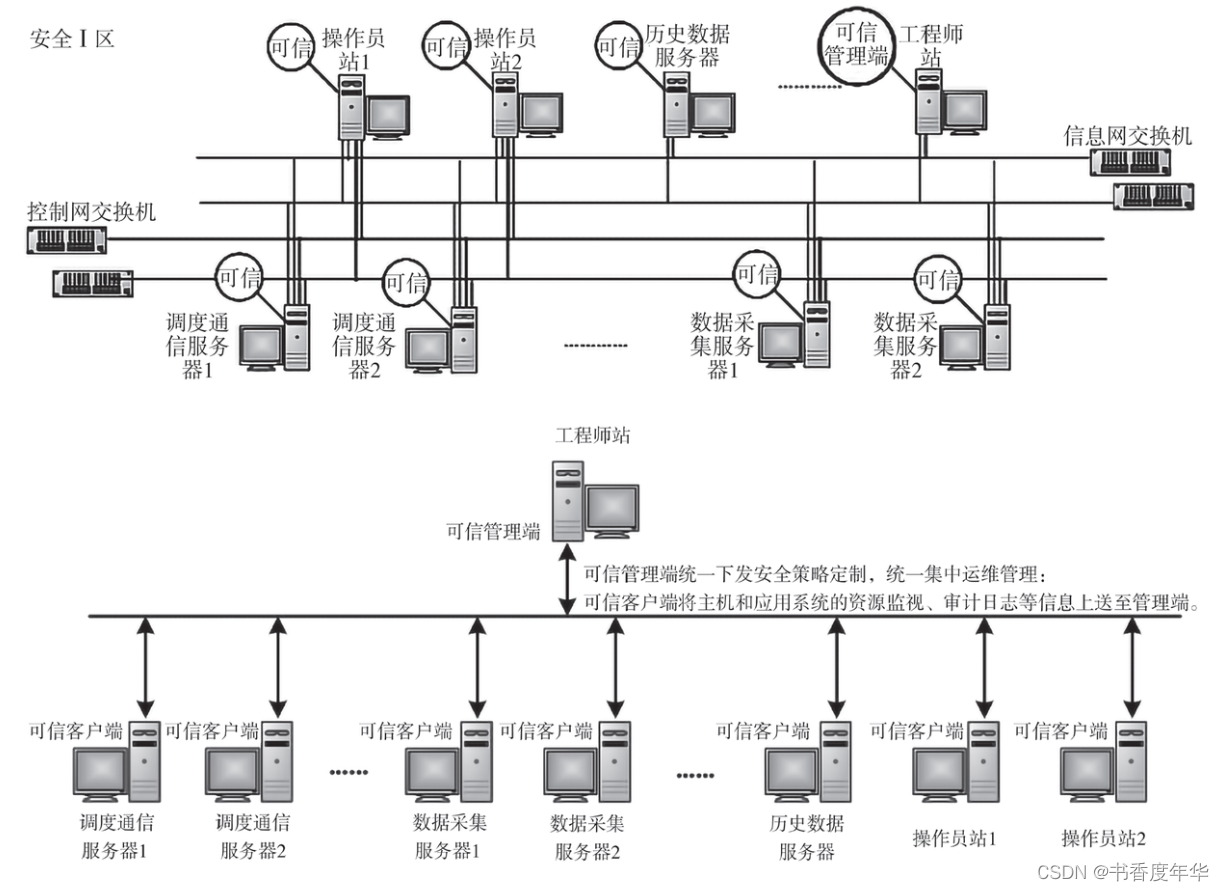
「可信计算」论文初步解读
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
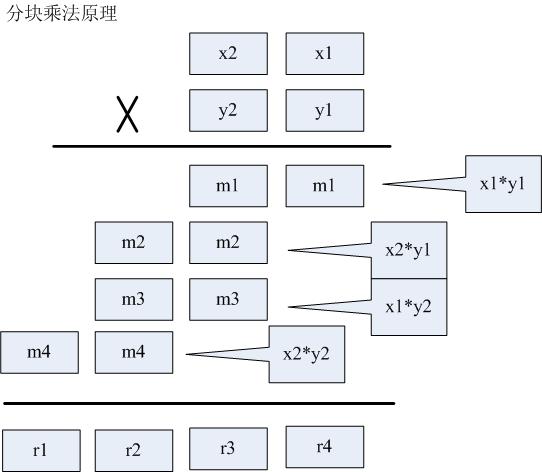
CSDN 算法技能树 蓝桥杯-基础 刷题+思考总结
切面条-蓝桥杯-基础-CSDN算法技能树https://edu.csdn.net/skill/algorithm/algorithm-530255df51be437b967cbc4524fe66ea?category188 目录 切面条 大衍数列 门牌制作 方阵转置 微生物增殖 成绩统计 星系炸弹 判断闰年的依据: 特别数的和 *日志统计*(双指…...
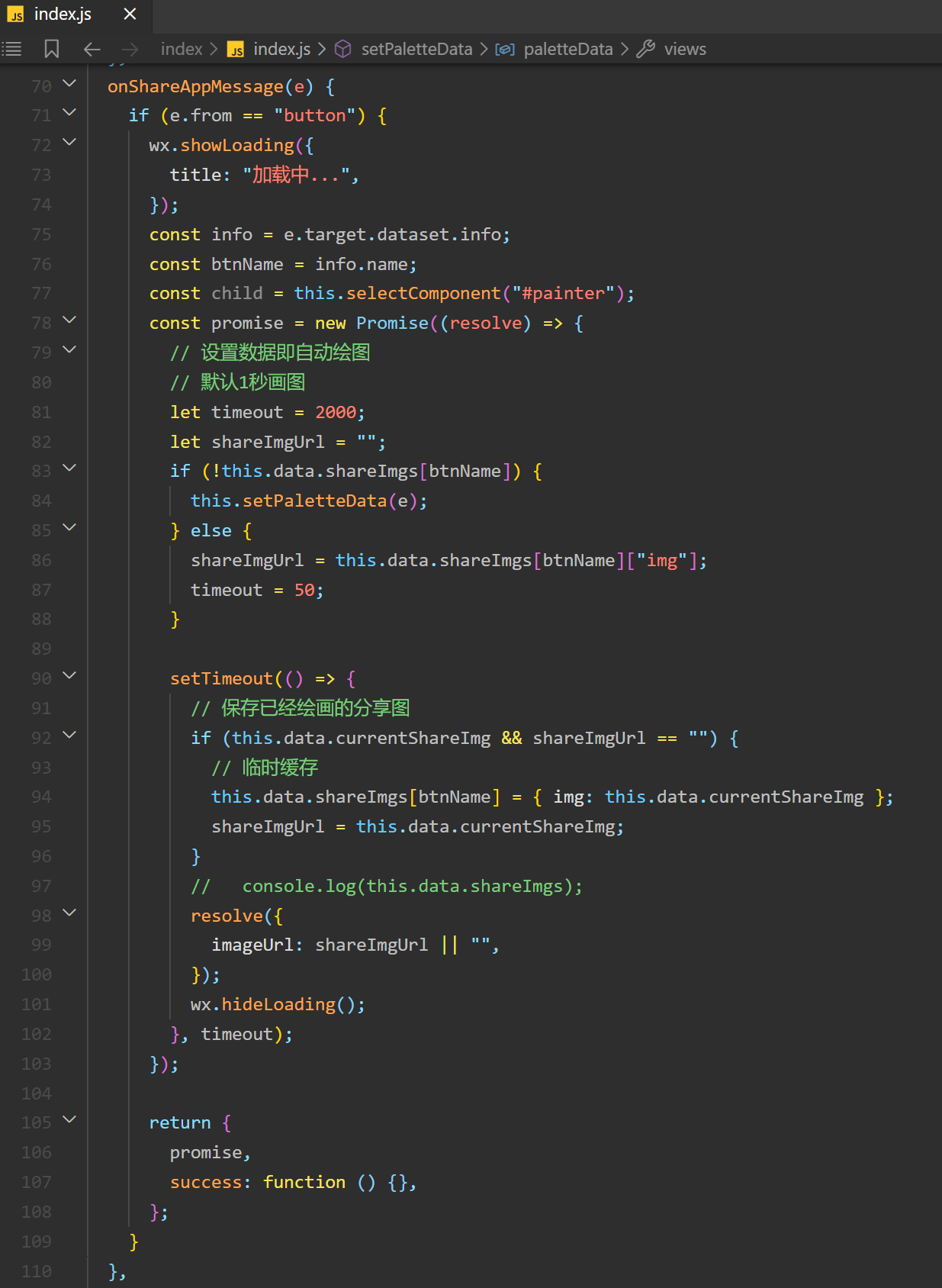
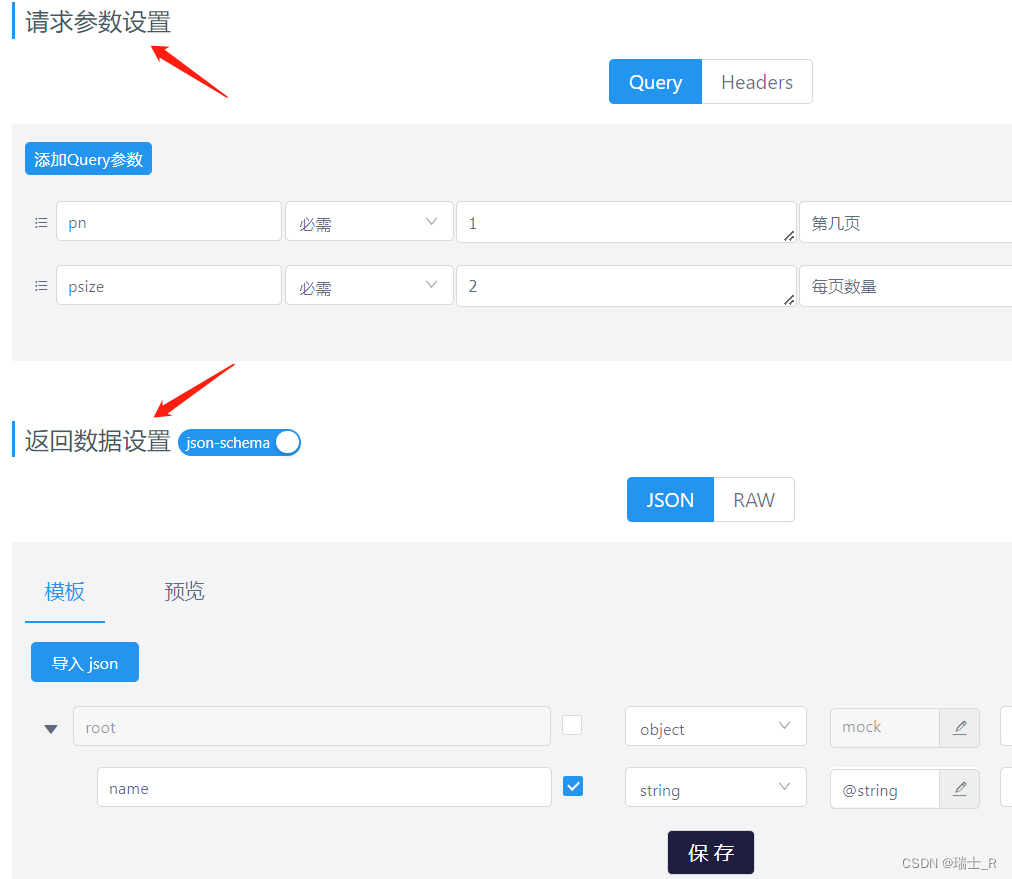
信小程序点击按钮绘制定制转发分享图
1. 说明 先上代码片断分享链接: https://developers.weixin.qq.com/s/vl3ws9mA72GG 使用 painter 画图 按钮传递定制化信息 效果如下: 2. 关键代码说明 文件列表如下: {"usingComponents": {"painter": "/com…...

Python自动化测试-使用Pandas来高效处理测试数据
Python自动化测试-使用Pandas来高效处理测试数据 目录:导读 一、思考 二、使用pandas来操作Excel文件 三、使用pandas来操作csv文件 四、总结 一、思考 1.Pandas是什么? 功能极其强大的数据分析库可以高效地操作各种数据集 csv格式的文件Excel文件H…...

语音增强学习路线图Roadmap
语音增强算是比较难的研究领域,从入门到精通有很多台阶,本文介绍一些有价值的书籍,值得反复阅读。主要分为基础类和进阶类书籍,大多都是理论和实践相结合的书籍,编程实践是抓手,让知识和基础理论变扎实。基础书籍《信号…...

nginx配置ssl实现https访问
文章目录一、介绍二、创建证书1、OpenSSL创建自签名密钥和证书三、nginx配置四、开放端口一、介绍 nginx配置ssl证书,实现https访问,可以使用自签名SSL证书或者购买机构颁发的证书两种方式参考链接 https://blog.csdn.net/weixin_39198406/article/deta…...

JavaScript 语句
JavaScript 语句向浏览器发出的命令。语句的作用是告诉浏览器该做什么。JavaScript 语句JavaScript 语句是发给浏览器的命令。这些命令的作用是告诉浏览器要做的事情。下面的 JavaScript 语句向 id"demo" 的 HTML 元素输出文本 "Hello Dolly" :…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...





