语言基础2 矩阵和数组
语言基础2 矩阵和数组
矩阵和数组是matlab中信息和数据的基本表示形式
可以创建常用的数组和网格 合并现有的数组 操作数组的形状和内容 以及使用索引访问数组元素
用到的函数列表如下

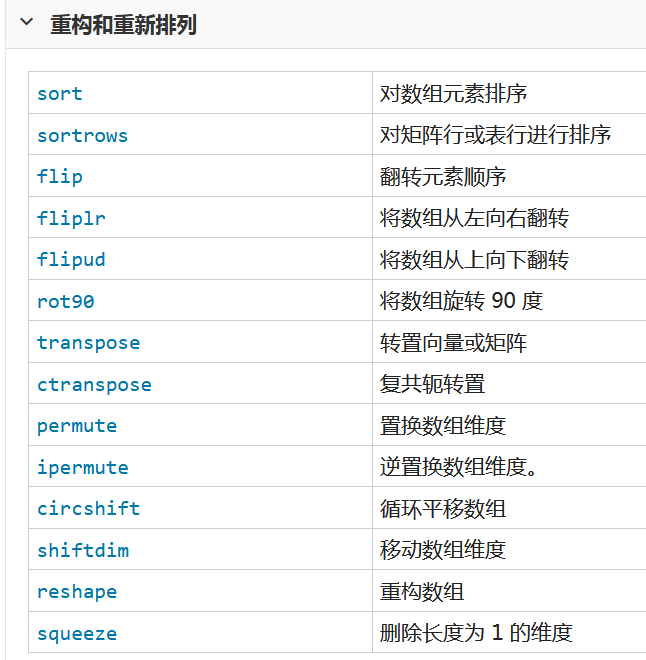

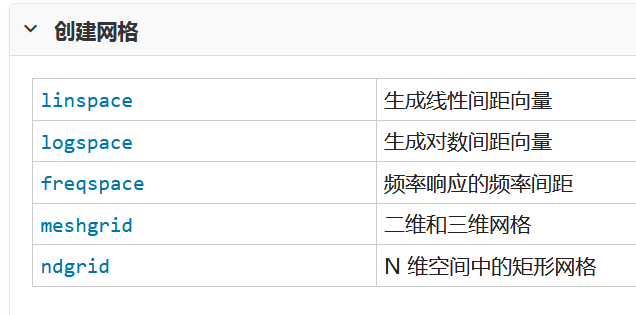
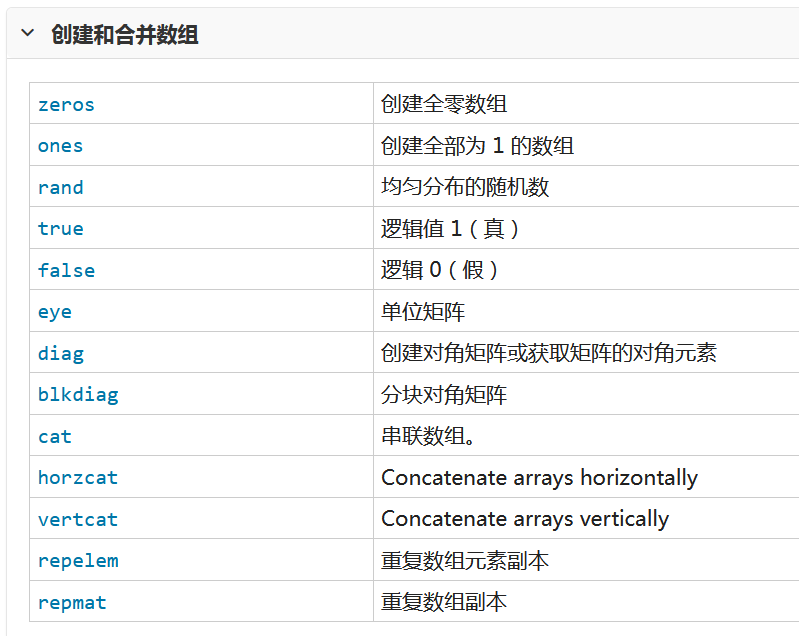
一 创建 串联和扩展矩阵
矩阵时按行和列排列的数据元素的二维数据元素的二维矩形数组。
元素可以是数字、逻辑值、日期时间、字符串、categorical、或其他matlab数据类型
>> A=100;
>> whos AName Size Bytes Class AttributesA 1x1 8 double
构建数据矩阵
>> A=[12 62 93 -8]
A =12 62 93 -8
>> whos AName Size Bytes Class AttributesA 1x4 32 double
>> A=[12 62;93 -8]
A =
12 62
93 -8
专用矩阵函数
zeros(n1,n2) n1行数 n2列数
ones(n1,n2)
>> zeros(2,3)
ans =0 0 00 0 0
>> ones(2,4)
ans =1 1 1 11 1 1 1
diag函数将输入元素放在矩阵的对角线上
>> A = [12 62 93 -8];
B = diag(A)
B =12 0 0 00 62 0 00 0 93 00 0 0 -8
串联矩阵
使用方括号来追加现有矩阵 此方法称为串联
>> A=ones(1,4);
>> B=zeros(1,4);
>> C=[A B]
C =1 1 1 1 0 0 0 0
串联多个矩阵 必须具有兼容的大小,水平串联矩阵时 行数必须相同,垂直串联矩阵,列数必须相同。
串联兼容矩阵的另一种方法时使用串联函数
horzcat vertcat cat
使用horzcat将第二个矩阵水平追加到第一个矩阵
>> D=horzcat(A,B)
D =1 1 1 1 0 0 0 0
使用vertcat将两个矩阵垂直连接
>> E=vertcat(A,B)
E =1 1 1 10 0 0 0
生成数值序列
colon 创建由连续且等间距元素组成的矩阵的便捷方式。例如创建一个行向量 其元素是从1到10的整数
>> A=1:10 默认增量为1
A =1 2 3 4 5 6 7 8 9 10
>> A=-2.5:2.5
A =-2.5000 -1.5000 -0.5000 0.5000 1.5000 2.5000
>> A=0:2:10 指定增量为2
A =0 2 4 6 8 10
>> A=6:-1:0 增量为负值 则递减
A =6 5 4 3 2 1 0
>> A=1:0.2:2.1 增量为非整形值 如果增量值不能平均分指定的范围 则会在超出范围之前在可以达到的最后一个值处自动结束序列 此处最后为2
A =1.0000 1.2000 1.4000 1.6000 1.8000 2.0000
扩展矩阵
通过想一个或多个元素置于现有行和列索引边界之外,可以将他们添加到矩阵中 matlab会自动用0填充矩阵,使其保持为举行
例如创建一个2x3矩阵 然后在(3,4)的位置插入一个元素 使矩阵增加一行一列
>> A=[10 20 30;60 70 80] %A 为2x3
A =10 20 3060 70 80
>> A(3,4)=1 此时(1,3)(2,3) 两个位置为0 此时A为3x4
A =10 20 30 060 70 80 00 0 0 1
还可以通过现有索引范围之外插入新矩阵来扩展其大小
>> A(4:5,5:6)=[2 3;4 5] 执行完成后 A为5x6 矩阵 未赋值的索引位置填0
A =10 20 30 0 0 060 70 80 0 0 00 0 0 1 0 00 0 0 0 2 30 0 0 0 4 5
上例中 A(4,5)=2 A(4,6)=3 A(5,5)=4 A(5,6)=5
如果重复扩展矩阵的大小 例如在for循环中,最好要为预计创建的最大矩阵预分配空间,matlab必须在每次大小增加时分配内存,所以时间开销较大。
可以预先生成一个大的全0矩阵
zeros(10000,10000) 行和列都是10000的矩阵
A=zeros(10000,10000) 如再大 需要再矩阵所以范围之外指定元素或将另一个预分配的矩阵与A串联来进行扩展
空数组
指至少有一个维度的长度等于零的数组 空数组可用于以编程方式表示“无”的概念
案例:
>> A=[1 2 3 4];
>> ind=find(A<0)
ind =空的 1×0 double 行向量
许多算法都包含可以返回空数组的函数调用 允许将空数组作为函数参数传递 而不是作为特殊情况处理。
需要自定义空数组的处理方式 可以使用isempty 函数来检查它们
TF=isempty(ind)
TF=logical
1 返回真值
数组索引
根据元素在数组中的位置(索引)访问数组元素的方法主要有三种:按位置索引、线性索引和逻辑索引。
按元素的位置进行索引
指定向量中的单个元素 : A(3,2) 行列式的方式 先给行号 再给列号
指定向量中的多个元素:A()
A = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]
a1=A(3,2) %3行2列 索引对应的值
a2=A(2,[1 3]) %A(2,1) A(2,3)
a3=A(1:3,2:4) % 访问第一到第三行、第二到第四列中的元素
a4=A(1:3,2:end) %end为最后一列
a5=A(:,3)%:表示所有行或所有列 此处表示所有行的第3列 全部数据输出:
A =1 2 3 45 6 7 89 10 11 1213 14 15 16
a1 =10
a2 =5 7
a3 =2 3 46 7 810 11 12
a4 =2 3 46 7 810 11 12
a5 =371115
通过索引来访问matlab中任何数组的元素 而不管其数据类型或维度如何 例如 直接访问datetime数组的列
datetime数组
>> datetime(2018,1:5,1) %详情参考 datetime()函数详情
ans = 1×5 datetime 数组2018-01-01 2018-02-01 2018-03-01 2018-04-01 2018-05-01
>> datetime(2018,1,1:5)
ans = 1×5 datetime 数组2018-01-01 2018-01-02 2018-01-03 2018-01-04 2018-01-05
使用单个索引进行索引
线性索引 实际上数据实际的存储方式都是按内存列式存储
>> A=[12 36 91;45 29 48;33 25 11]
A =12 36 9145 29 4833 25 11
>> Alinear=A(:) %显示全部
Alinear =124533362925914811
>> A(6) 按列序 定值
ans =25
>> A(3,2) 按二维数组坐标索引定值
ans =25
>> s=sum(A(:))
s =
330
sub2ind 和 ind2sub 函数可用于在数组的原始索引和线性索引之间进行转换 例如计算A的第3,2个元素的线性索引。
>> linearidx=sub2ind(size(A),3,2) % 将行,列的形式转换为线性索引单列的形式 所以(3,2)对应单列为6 返回值为6
linearidx =6
>> [row,col]=ind2sub(size(A),6) % 将单列的线性索引形式转换为行,列定位的形式 返回2个输出的变量
row =3
col =2
使用逻辑值进行索引
使用true和false 逻辑指示符也可以对数组进行索引 在处理条件语句时尤其便利。
例如 假设想知道A中的元素是否小于另一个矩阵B中的对应元素
当A中的元素小于B中的对应元素时,小于号运算符返回元素为1的逻辑数组。
>> A=[1 2 6;4 3 6]
A =1 2 64 3 6
>> B=[0 3 7;3 7 5]
B =0 3 73 7 5
>> ind=A<B %判断A和B的各个对应元素 是否满足小于关系 是为1 否为0
ind =2×3 logical 数组0 1 10 1 0
上例中得到了满足条件的元素的位置;
已经可以使用ind作为索引数组来检查各个值
matlab 将ind中值1的位置与A和B中的对应元素进行匹配,并在列向量中列出它们的值。
>> Avals=A(ind) 列出A中的值
Avals =236
>> Bvals=B(ind) 列出B中的值
Bvals =377
is函数还返回逻辑数组 指示输入中的哪些元素满足特定条件。
ismissing函数检查string向量中的哪些元素时缺失值。
>> str=["A" "B" missing "D" "E" missing];
>> ind=ismissing(str) 返回一个索引数组 对应值为1的索引位置的字符缺失 原字符数组中包含missing的索引位置为1 其余为0
ind =1×6 logical 数组 0 0 1 0 0 1
假设要查找非缺失值元素的值 将~运算符和索引向量ind结合使用即可实现此目的
>> strvals=str(~ind) %
strvals = 1×4 string 数组"A" "B" "D" "E"
查找符合条件的数组元素
通过对数组应用条件来过滤数组元素。
检查矩阵中的偶数元素、查找多维数组中所有0值的位置,或者替换数据中的NaN值。
通过组合使用关系运算符和逻辑运算符来执行这些任务。
> < <= == ~= 逻辑运算符 and or not 分别用& | ~表示 从而应用多个条件。
应用单个条件
rng default 创建一个5x5矩阵 元素为位于1和15之间的随机整数
A=randi(15,5) randi(imax,n) 返回5x5矩阵 其中包含从区间[1,imax]的均匀离散分布中得到的伪随机整数
A =
13 2 3 3 1014 5 15 7 12 9 15 14 1314 15 8 12 1510 15 13 15 11
>> B=A<9 使用小于号关系运算符 确定A中的哪些元素小于9 将结果存储在B中
B =5×5 logical 数组0 1 1 1 00 1 0 1 11 0 0 0 00 0 1 0 00 0 0 0 0 B为逻辑矩阵 每个值都表示为逻辑值的状态 符合的元素索引位置为1 否则为0 假
>> A(B) B中不会指出这些元素的具体值是多少 但是可以使用B创建A的索引 从而得出满足条件的值
ans = 以列的形式展示出来22538371
由于B为逻辑矩阵 所以上面的运算称为逻辑索引
有时某些问题需要符合条件的数组元素的位置信息 而非其实际值。
案例可以使用find函数来查找A中小于9的所有元素
>> I=find(A<9)
I =3671114161722 返回的是一个由线型索引组成的列向量 每个索引描述A中一个小于9的元素的位置 因此实际上A(I)与A(B)返回的结果相同
差别为A(B) 使用逻辑索引 而A(I)使用线性索引
应用多个条件
使用and or not 运算符将任意多个条件应用于一个数组;条件的数量并不局限于一个或两个。
首先,使用逻辑and运算符 由&表示 指定两个条件:元素必须小于9且大于2 将这些条件指定为逻辑索引 以查看符合两个条件的元素。
>> A(A<9 & A>2)
ans =53837
结果为A中同时符合这两个条件的元素的列表。
务必使用单独的语句指定每个条件,并用逻辑运算符连接起来。
例如:
不能通过A(2<A<9)指定以上条件,因为其计算结果为A(2<A|A<9).
接下来,查找A中小于9且为偶数的元素。
>> A(A<9&~mod(A,2))
ans =228 线型排序 列向 显示A中小于9的所有偶数元素的列表 使用逻辑NOT运算符~将矩阵mod(A,2)转换为逻辑矩阵
并在可被2整除的元素位置防止逻辑值1 true
案例2:
查找A中小于9 为偶数且不等于2的元素
>> A(A<9&~mod(A,2)&A~=2) 返回具体的值
ans =8
>> find(A<9&~mod(A,2)&A~=2) 返回元素所在的位置 索引 线性索引
ans = 14 即A(14)=8
替换符合条件的值
同时更改多个现有数组元素的值会很有用。将逻辑索引与简单的赋值语句一起使用,可替换数组中符合条件的值。
将A中所有大于10的所有值替换为数值10
>> A(A>10)=10
A =10 2 3 3 1010 5 10 7 12 9 10 10 1010 10 8 10 1010 10 10 10 10
>>
>> A(A~=10)=NaN %将A中不等于10的所有值替换为NaN值
A =10 NaN NaN NaN 1010 NaN 10 NaN NaNNaN NaN 10 10 1010 10 NaN 10 1010 10 10 10 10
>> A(isnan(A))=0; 将A中所有NaN值替换为0 并应用逻辑NOT运算符 ~A
>> C=~A
C =
5×5 logical 数组
0 1 1 1 0
0 1 0 1 1
1 1 0 0 0
0 0 1 0 0
0 0 0 0 0
生成矩阵用逻辑值1 替代NaN值 用逻辑值0取代10 逻辑NOT运算~A将数值数组转换为逻辑数组,因此A&C返回逻辑值0 的矩阵 A|C返回逻辑值1的矩阵。
相关文章:

语言基础2 矩阵和数组
语言基础2 矩阵和数组 矩阵和数组是matlab中信息和数据的基本表示形式 可以创建常用的数组和网格 合并现有的数组 操作数组的形状和内容 以及使用索引访问数组元素 用到的函数列表如下 一 创建 串联和扩展矩阵 矩阵时按行和列排列的数据元素的二维数据元素的二维矩…...

springMVC中过滤器抛出异常,自定义异常捕获
在过滤器中引入org.springframework.web.servlet.HandlerExceptionResolver AutowiredQualifier("handlerExceptionResolver")private HandlerExceptionResolver resolver; // doFilter中处理if (条件1) {if (条件2) {resolver.resolveException(request, response, …...

图像检索技术研究:深度度量与深度散列在相似性学习中的应用比较与实践 - 使用Python与Jupyter环境
引言 在计算机视觉领域,图像检索是一个长期存在并持续受到研究者关注的重要话题。随着大数据时代的到来,如何高效、准确地从海量数据中检索到相似的图像成为一个巨大的挑战。传统的检索方法在大数据环境下表现不佳,而深度学习技术的崛起为图…...

CSS加载失败的6个原因
有很多刚刚接触 CSS 的新手有时会遇到 CSS 加载失败这个问题,但测试时,网页上没有显示该样式的问题,这就说明 CSS 加载失败了。出现这种状况一般是因为的 CSS 路径书写错,或者是在浏览器中禁止掉了 CSS 的加载,可以重新…...
react之路由的安装与使用
一、路由安装 路由官网2021.11月初,react-router 更新到 v6 版本。使用最广泛的 v5 版本的使用 npm i react-router-dom5.3.0二、路由使用 2.1 路由的简单使用 第一步 在根目录下 创建 views 文件夹 ,用于放置路由页面 films.js示例代码 export default functio…...

基于RoCE的应用程序的MTU注意事项
目录 基于RoCE的应用程序的MTU注意事项 探测网络中的MTU设置 概要 原文 MTU测试结果 DOC: CentOS安装tshark抓包工具 基于RoCE的应用程序的MTU注意事项 原文:https://support.mellanox.com/s/article/MLNX2-117-1682kn InfiniBand协议最大传输单元ÿ…...

springboot集成Graphql相关问题汇总
1、idea在debug运行时出现java.lang.NoClassDefFoundError:kotlin/collections/AbstractMutableMap 解决:禁用idea dubugger中kotlin coroutine agent 见:https://stackoverflow.com/questions/70796177/after-the-spring-boot-source-code-is-compile…...

Angular16的路由守卫基础使用
Angular16的路由守卫基础使用 使用ng generate guard /guard/login命令生成guard文件因新版Angular取消了CanActivate的使用,改用CanActivateFn,因此使用router跳转需要通过inject的方式导入。 import { inject } from angular/core; import { CanActi…...

leetcode228. 汇总区间
题目 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说,nums 的每个元素都恰好被某个区间范围所覆盖,并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区间范围 [a,b]…...

删除有序链表中重复的元素-II(链表)
乌!蒙!山!连!着!山!外!山! 题目: 思路: 双指针,slow和fast,并且增加标记flag初始为1。 如果slow指向节点值等于fast指向节点值&…...

element单独检验form表单中的一项
<el-form-item prop"limitDays" style"margin-left: 5px;"><el-input v-model"ruleForm.limitDays" placeholder"天数" style"width: 100px;" /> </el-form-item> <el-form-item prop"limitCount…...

Webpack node、output.jsonpFunction 配置详解
Webpack node、output.jsonpFunction 配置详解 最近尝试给一些用到 webpack 的项目升级到最新 webpack5 版本,其中遇到了一些问题,我挑了两个比较典型的问题,其中主要涉及到了 webpack 的 node 属性跟 output.jsonpFunction (web…...

要跟静音开关说再见了!iPhone15新变革,Action按钮引领方向
有很多传言称iPhone 15 Pro会有很多变化,但其中一个变化可能意味着iPhone体验从第一天起就有的一项功能的终结。我说的是静音开关,它可以让你轻松地打开或关闭iPhone的铃声。 根据越来越多的传言,iPhone 15 Pro和iPhone 15 Pro Max将拆除静音…...

论文笔记 Graph Attention Networks
2018 ICLR 1 intro 1.1. GCN的不足 无法完成inductive任务 inductive任务是指: 训练阶段与测试阶段需要处理的graph不同。通常是训练阶段只是在子图上进行,测试阶段需要处理未知的顶点。GGN 的参数依赖于邻接矩阵A/拉普拉斯矩阵L,所以换了…...

看上去就很像的agree和degree有什么联系
“Agree”(同意)和 “degree”(程度)这两个词在语义上没有直接的联系,它们代表不同的概念。 “Agree” 意味着在意见、观点或立场上达成共识或一致。它表示同意或同意某人或某事。 例如: “We all agree…...
)
2023前端面试题第二弹(真实,一般人我还不给看)
为什么要初始化css? 避免浏览器差异,解决兼容问题 网格布局 display: grid; grid-template-columns: 1fr 1fr 1fr less的优点 可以兼容,可以嵌套,循环,运算,定义变量和继承样式(extendÿ…...

零基础如何学习 Web 安全,如何让普通人快速入门网络安全?
前言 网络安全现在是朝阳行业,缺口是很大。不过网络安全行业就是需要技术很多的人达不到企业要求才导致人才缺口大 【一一帮助安全学习(网络安全面试题学习路线视频教程工具)一一】 初级的现在有很多的运维人员转网络安全,初级…...
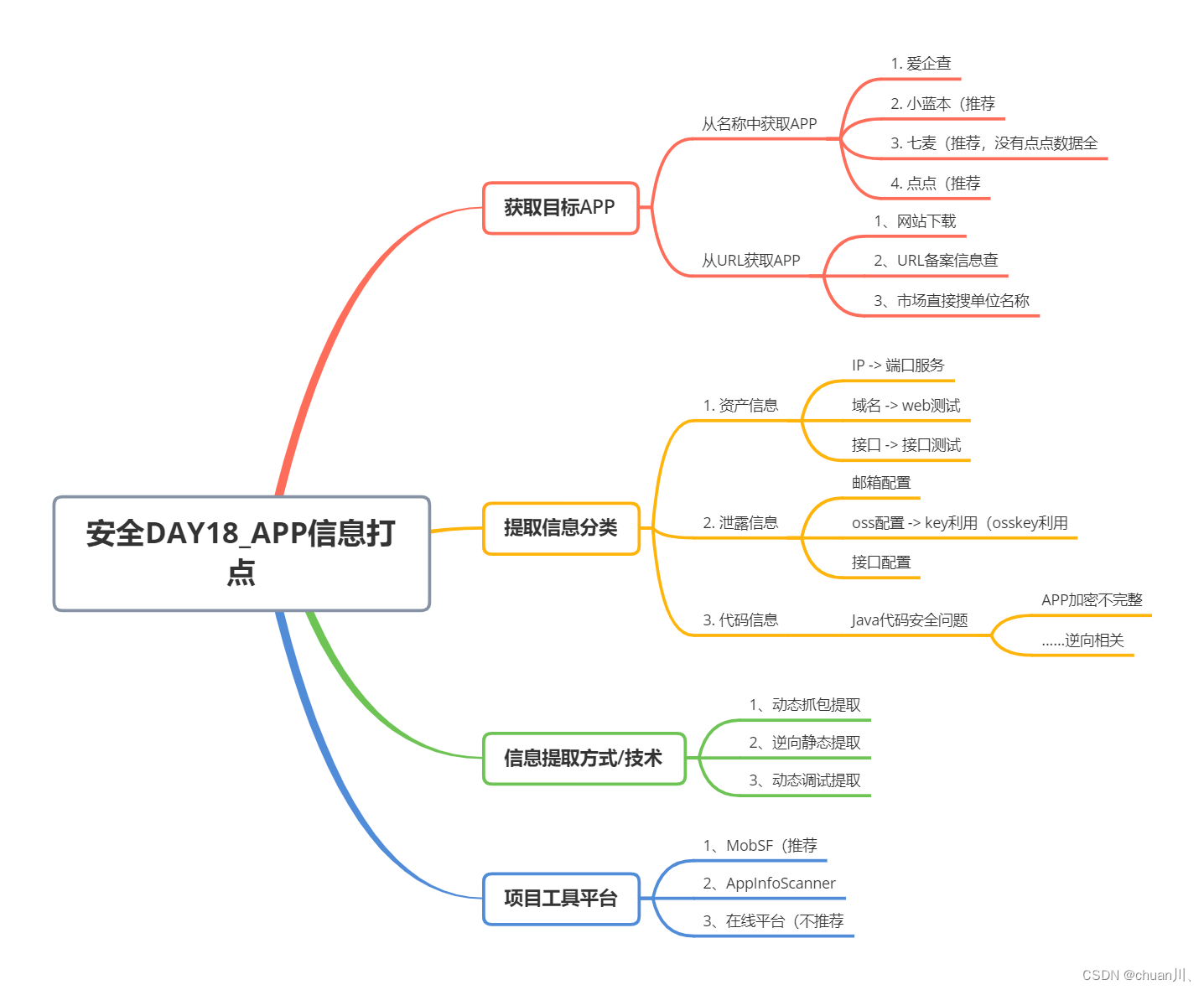
安全学习DAY18_信息打点-APP资产搜集
信息打点-APP资产&静态提取&动态抓包&动态调试 文章目录 信息打点-APP资产&静态提取&动态抓包&动态调试本节知识&思维导图本节使用到的链接&工具 如何获取目标APP从名称中获取APP从URL获取APP APP搜集资产信息APP提取信息分类信息提取方式信息…...

react 矩形波浪
"矩形波浪"(Square Wave)在信号处理和波形生成中是一种特殊类型的波形,通常由两个不同的值交替组成,一个是高电平,另一个是低电平,形成类似方波的波形。在 React 中创建一个矩形波浪的效果可以通…...
【GitHub】Pycharm本地项目打包上传到Github仓库的操作步骤
文章目录 1、Pycharm端的设置操作2、Github端的设置操作3、Pycharm上配置Github4、Git本地项目至GitHub仓库5、前往Github中查看确认6、常见报错 1、Pycharm端的设置操作 通过CtrlAltS快捷组合键的方式,打开设置,导航到版本控制一栏中的Git,…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
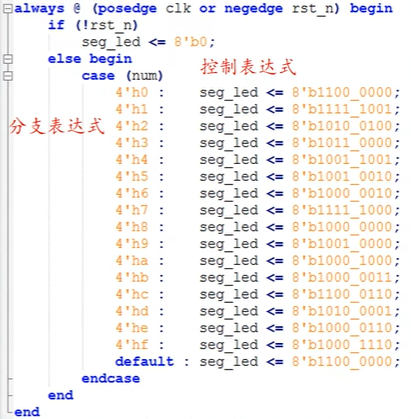
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...

uniapp获取当前位置和经纬度信息
1.1. 获取当前位置和经纬度信息(需要配置高的SDK) 调用uni-app官方API中的uni.chooseLocation(),即打开地图选择位置。 <button click"getAddress">获取定位</button> const getAddress () > {uni.chooseLocatio…...
:PyQuery 框架)
Python爬虫(四):PyQuery 框架
PyQuery 框架详解与对比 BeautifulSoup 第一部分:PyQuery 框架介绍 1. PyQuery 是什么? PyQuery 是一个 Python 的 HTML/XML 解析库,它采用了 jQuery 的语法风格,让开发者能够用类似前端 jQuery 的方式处理文档解析。它的核心特…...
