华为OD真题--分月饼--带答案
1. 华为OD机考题 + 答案
2023华为OD统一考试(A+B卷)题库清单-带答案(持续更新)
2023年华为OD真题机考题库大全-带答案(持续更新)
2. 面试题
一手真实java面试题:2023年各大公司java面试真题汇总--持续更新
3. 技术知识
java后端技术汇总 + 中间件 + 架构思想
题目描述:
公司分月饼,m个员工,买了n个月饼,m <= n,每个员工至少分一个月饼,但是也可以分到多个,单人分到最多月饼的个数是Max1,单人分到第二多月饼个数是Max2。
但需要满足Max1-Max2 <= 3,单人分到第n-1多月饼个数是Max(n-1),单人分到第n多月饼个数是Max(n), 想要满足Max(n-1) - Max(n) <= 3,问有多少种分月饼的方法?
输入描述:
每一行输入m,n,表示m个员工,n个月饼,m <=n
输出描述:
输出有多少种分法
示例1:
输入
2 4
输出
2
说明
4=1+3
4=2+2
注意:1+3和3+1要算成同一种分法
示例2:
输入
3 5
输出
2
说明
5=1+1+3
5=1+2+3
示例3:
输入
3 12
输出
6
说明
满足要求的6种分法:
1、12 = 1 + 1 + 10 (Max1=10, Max2=1,不满足Max1-Max2 <= 3的约束)
2、12 = 1 + 2 + 9 (Max1=9,Max2=2,不满足Max1-Max2 <= 3的约束)
3、12 = 1 + 3 + 8 (Max1=8,Max2=3,不满足Max1-Max2 <= 3的约束)
4、12 = 1 + 4 + 7 (Max1=7,Max2=4,Max3=1, 满足要求)
5、12 = 1 + 5 + 6 (Max1=6,Max2=5,Max3=1, 不满足要求)
6、12 = 2 + 2 + 8 (Max1=8,Max2=2,不满足要求)
7、12 = 2 + 3 + 7 (Max1=7,Max2=3,不满足要求)
8、12 = 2 + 4 + 6 (Max1=6,Max2=4,Max3=2, 满足要求)
9、12 = 2 + 5 + 5 (Max1=5,Max2=2 满足要求)
10、12 = 3 + 3 + 6 (Max1=6,Max2=3 满足要求)
11、12 = 3 + 4 + 5 (Max1=5,Max2=4,Max3=3 满足要求)
12 = 4 + 4 + 4 (Max1=4,满足要求)
public class DivideMooncake {
//非最优解,需要考虑减枝,减少遍历次数。public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int [] num = Arrays.stream(scanner.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();//分配人数int peoples = num[0];//待分配数量int dnum = num[1] - num[0];//重新分配后每个人月饼数量int [] nums = new int[peoples];// 用一个List来存储所有分配方案List<List<Integer>> result = new ArrayList<>();divide(dnum,peoples,nums,result);List<List<Integer>>filteredResult = removeDuplicate(result);//System.out.println(filteredResult);System.out.println(filteredResult.size());}public static void divide(int num,int peolpe, int [] nums,List<List<Integer>> result){if (peolpe == 1){nums[0] = num;List<Integer> allocation = new ArrayList<>();for (int i : nums){allocation.add(i);}result.add(allocation);return;}for (int i = 0; i <= num ; i++){//要分配的月饼nums[peolpe - 1] = i;//递归调用,将要分配的月饼分配给其它人divide(num - i,peolpe -1,nums,result);}}/*** 判断是否满足条件 Max(n) - Max(n-1) >= 3* @param nums* @return*/public static Boolean satisfy(List<Integer> nums){int i = nums.size() -1;while (i >= 1){if (nums.get(i) - nums.get(i - 1) > 3){return false;}i--;}return true;}/*** 分数一致的去重* @param result* @return*/public static List<List<Integer>> removeDuplicate(List<List<Integer>> result) {List<List<Integer>> filteredResult = new ArrayList<>();for (List<Integer> allocation : result) {boolean duplicate = false;allocation.sort(Integer::compareTo); // 对分配方案进行排序for (List<Integer> existingAllocation : filteredResult) {existingAllocation.sort(Integer::compareTo); // 对已有的分配方案进行排序if (Arrays.equals(existingAllocation.toArray(), allocation.toArray())) {duplicate = true; // 分配方案重复break;}}if (!duplicate) {if (satisfy(allocation)){filteredResult.add(allocation);}}}return filteredResult;}}相关文章:

华为OD真题--分月饼--带答案
1. 华为OD机考题 答案 2023华为OD统一考试(AB卷)题库清单-带答案(持续更新) 2023年华为OD真题机考题库大全-带答案(持续更新) 2. 面试题 一手真实java面试题:2023年各大公司java面试真题汇总--…...
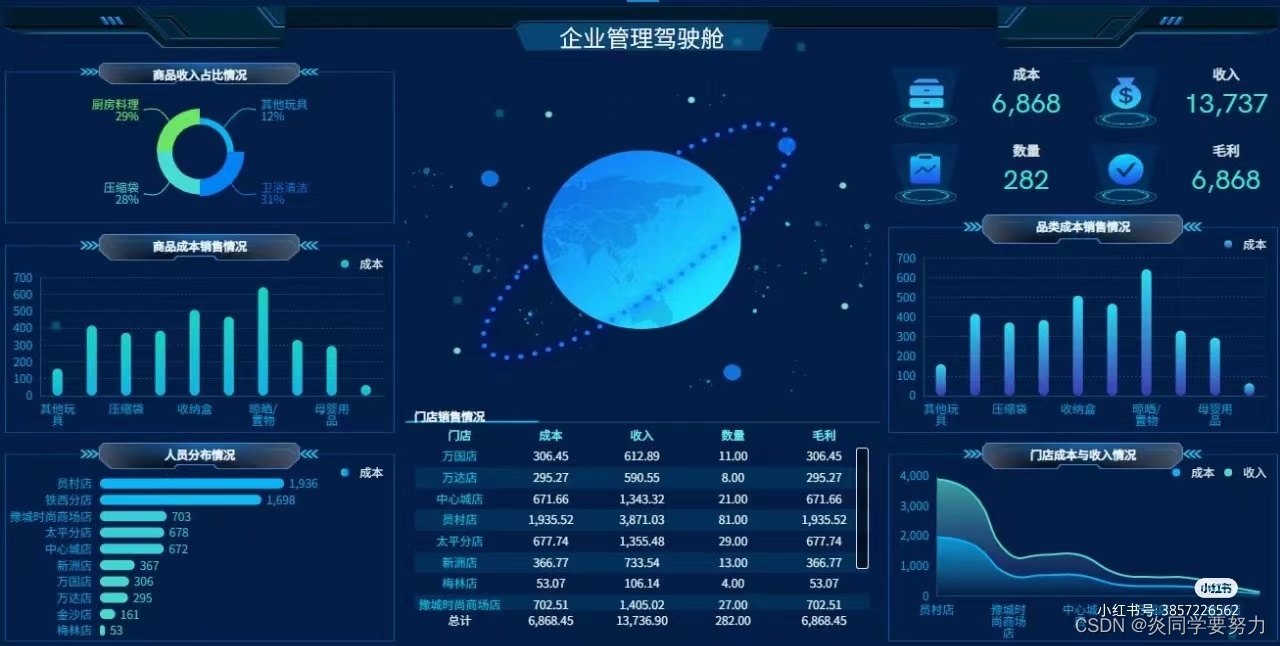
帆软大屏2.0企业制作
 数字化观点中心 / 当前页 如何从0-1制作数据大屏,我用大白话给你解释清楚了 文 | 商业智能BI相关文章 阅读次数:18,192 次浏览 2023-06-08 11:51:49 好莱坞大片《摩天营救》中有这么一个场景:  你可以看见反派大b…...
【学习笔记之opcua】使用Python获取opcua数据
Python与OPC UA的应用 示例代码 将代码放入spyder中运行后,出现下面这个错误 没有‘opcua’,那我们就下载pip install opcua 之后出现下面这个错误 问问题大不,安装语句写错了 正经安装语句是 !pip install opcua 读取opcua协议数据测试 …...

apache doris和StarRocks的区别
记录一下最新要用到2个新数据库的区别 Apache Doris是一个分布式的列式存储系统,它的设计目标是提供大规模数据处理的可靠性和高性能。Doris采用了集群方式,通过将数据分布在多个机器上进行处理来提高性能,并提供了SQL查询接口方便用户使用。…...

文心一言最新重磅发布!
8月16日,由深度学习技术及应用国家工程研究中心主办的WAVE SUMMIT深度学习开发者大会2023举办。百度首席技术官、深度学习技术及应用国家工程研究中心主任王海峰以《大语言模型为通用人工智能带来曙光》为题,阐述了大语言模型具备理解、生成、逻辑、记忆…...

css整体使用
文章目录 html与csshtml、css与排版响应式与自适应布局自适应布局响应式布局 css规则class、id、以及默认的标签名的优先级 css书写位置flex整体逻辑 bootstrap资源 html与css html负责网页功能,css负责网页美化;浏览器本身有一套默认的css样式…...

LeetCode1578. 使绳子变成彩色的最短时间
思路 拆除成本 全部拆除 - 最大的不拆除在统计成本的同时,维持一个成本的最大值 代码 class Solution {public int minCost(String colors, int[] neededTime) {int res 0;int i 0;int len colors.length();while (i < len) {int max -1;int sum 0;char…...

如何在机器学习中实现分类?
机器学习和统计学中的分类是一种监督学习方法,其中计算机程序从给定的数据中学习并进行新的观察或分类。在本文中,我们将详细了解机器学习中的分类。 本博客涵盖以下主题: 目录 什么是机器学习中的分类? 机器学习中的分类术语 分类算法...
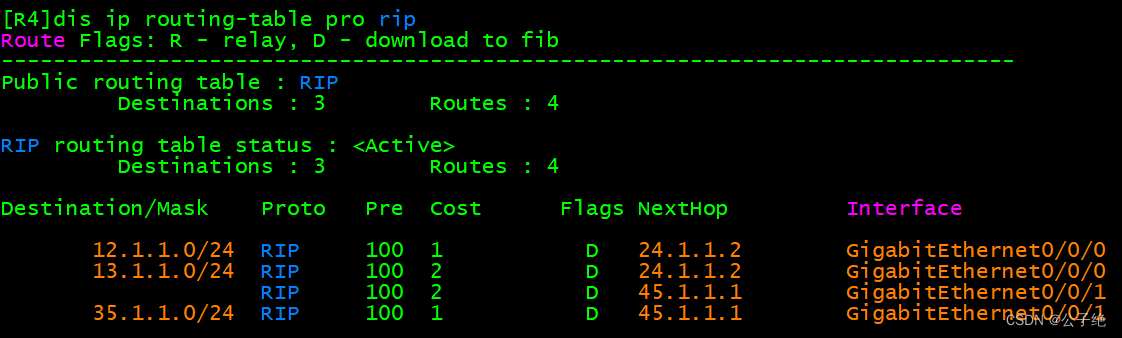
华为网络篇 RIP的负载均衡-29
难度2复杂度2 目录 一、实验原理 二、实验拓扑 三、实验步骤 四、实验过程 总结 一、实验原理 RIP是使用跳数(经过路由的数量)作为metric值的,当网络上存在去往目标的路由有两条以上都是相同metric时,就出现了流量负载均衡。…...
每天10个小知识点)
前端面试的性能优化部分(10)每天10个小知识点
目录 系列文章目录前端面试的性能优化部分(1)每天10个小知识点前端面试的性能优化部分(2)每天10个小知识点前端面试的性能优化部分(3)每天10个小知识点前端面试的性能优化部分(4)每天…...

分类预测 | MATLAB实现S4VM半监督支持向量机二分类预测
分类预测 | MATLAB实现S4VM半监督支持向量机二分类预测 目录 分类预测 | MATLAB实现S4VM半监督支持向量机二分类预测分类效果基本介绍程序设计参考资料 分类效果 基本介绍 分类预测 | MATLAB实现S4VM半监督支持向量机二分类预测 程序设计 完整源码和数据获取方式: …...

maven -pl -am -amd
maven常见命令之 -pl -am -amd 昨天maven的deploy任务需要只选择单个模块并且把它依赖的模块一起打包,第一时间便想到了-pl参数,然后就开始处理,但是因为之前只看了一下命令的介绍,竟然花了近半小时才完全跑通,故记录…...
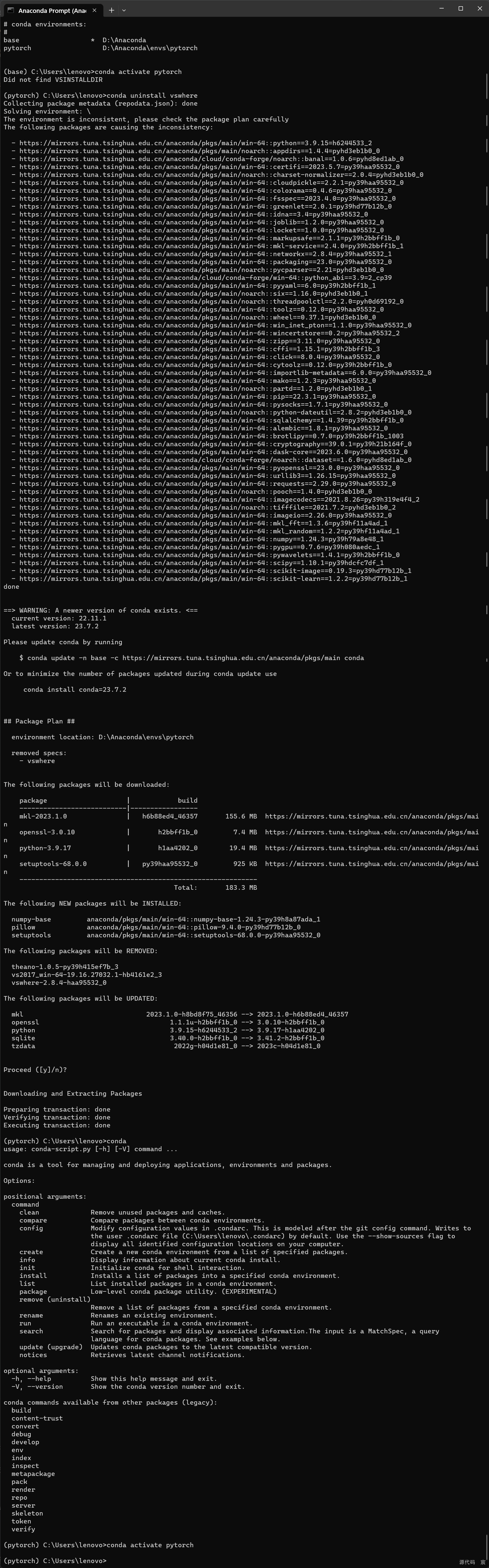
高效解决Anaconda Prompt报错Did not find VSINSTALLDIR这类问题
文章目录 回忆问题解决问题step1step2 回忆问题 类似于划红线部分然后还有很多行的报错信息,最后一行肯定是红色划线部分 解决问题 step1 找到 D:\Anaconda\envs\pytorch\etc\conda\activate.d在这个文件夹内会有两个文件,删除 vs2017_compiler_v…...

将iPhone备份到移动硬盘
文章目录 将iPhone备份到移动硬盘如何在 MacOS 上查找当前备份如何在 MacOS 上查找当前备份如何将 iPhone 备份移至外部硬盘如何永久更改 Mac系统 保存 iPhone 备份的位置更新 Mac 上的权限更改 iPhone 备份位置如何验证新的 iPhone 备份已经生效?将iPhone备份到移动硬盘 如果…...

找工作 相关资料
1、简历准备 一份近乎完美的计算机简历应该如何写以及如何修改?-知乎 2.1 机械面试可能的问题 2.1.1 技术邻上的 机械专业面试31问 2.1.2 B站上的 B站: “经常作为面试题,50个机械设计基础常识,你掌握了几个?”文…...

罗勇军 → 《算法竞赛·快冲300题》每日一题:“排列变换” ← 贪心算法
【题目来源】http://oj.ecustacm.cn/problem.php?id1812http://oj.ecustacm.cn/viewnews.php?id1023【题目描述】 给定一个长度为 n 的排列 a,需要将这个排列变成 b。 每次可以选择一个数字往左移若干个位置。 请求出最小需要移动的元素个数。【输入格式】 第一行…...

算法修炼Day51|● 309.最佳买卖股票时机含冷冻期 ● 714.买卖股票的最佳时机含手续费
LeetCode:309.最佳买卖股票时机含冷冻期 309. 买卖股票的最佳时机含冷冻期 - 力扣(LeetCode) 1.思路 初始化dp[i][j]数组,表示第i天的最大利润为dp[i][j]. 精确的定义状态是个难点,可以定义四种状态:持有股票&#…...
LVS-DR模型实例
一、LVS-DR集群介绍 LVS-DR(Linux Virtual Server Director Server)工作模式,是生产环境中最常用的一 种工作模式。 1、LVS-DR 工作原理 LVS-DR 模式,Director Server 作为群集的访问入口,不作为网关使用࿰…...

Vue面试题
1. vue优点 轻量级速度快简单易学低耦合可重用性独立开发文档齐全,且文档为中文文档 2. ## vue中组件间传值 prop/$emit 父子组件传值 ref 和 $parent/$children 父子组件传值 eventBus($emit/$on) 父子,隔代,兄弟组件传值 $attrs/$listeners…...

使用图像处理算法检测金属表面的生锈区域: Python实现及步骤解析
摘要: 本文主要介绍如何使用Python和OpenCV库来实现对金属表面的生锈区域的检测。图像处理在工业领域有着广泛的应用,尤其是对材料的表面缺陷的检测。本文将详细阐述该算法的具体实现步骤,并提供完整的Python代码示例。 1. 引言 金属的锈蚀是…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
