matlab使用教程(19)—曲线拟合与一元方程求根
1.多项式曲线拟合
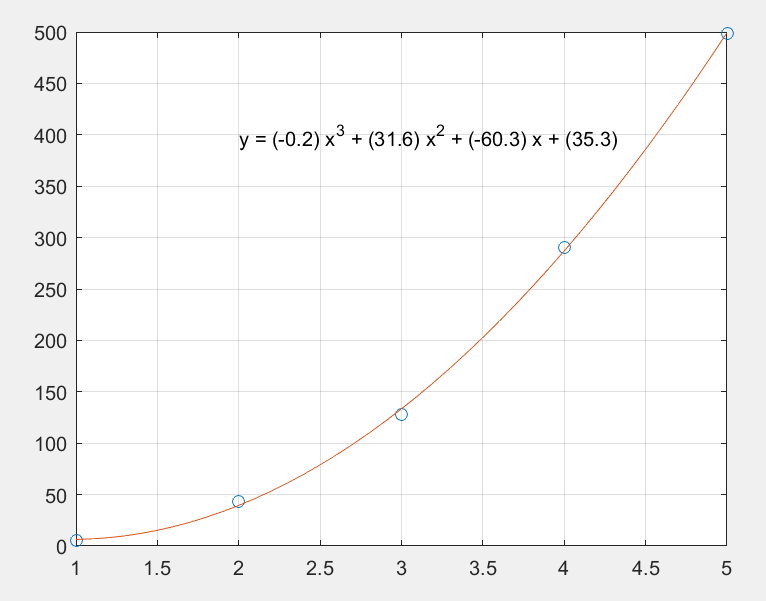
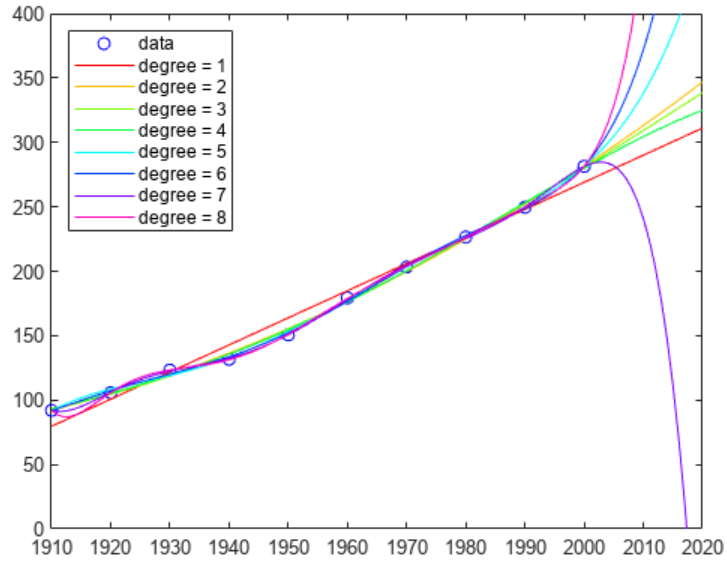
1.1 预测美国人口

那么猜想一下 2010 年美国的人口是多少?


2.标量函数的根
2.1 对一元非线性方程求解
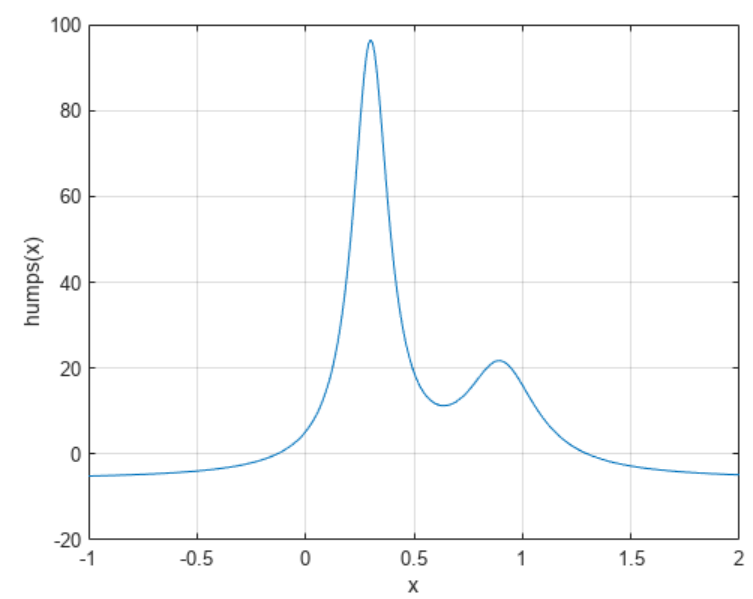
2.2 为 fzero 设置选项
2.3 使用起始区间
相关文章:

matlab使用教程(19)—曲线拟合与一元方程求根
1.多项式曲线拟合 此示例说明如何使用 polyfit 函数将多项式曲线与一组数据点拟合。您可以按照以下语法,使用 polyfit 求出以最小二乘方式与一组数据拟合的多项式的系数 p polyfit(x,y,n), 其中: • x 和 y 是包含数据点的 x 和 y 坐标的向量 …...

【Go 基础篇】Go语言关键字和预定义标识符解析:探索编程的基石与核心要素
介绍 在计算机编程中,关键字(Keywords)和预定义标识符(Predefined Identifiers)是编程语言的核心要素,它们在语法结构和语言功能中起到重要作用。在Go语言(Golang)中,关…...

微服务与Nacos概述-6
RBAC 模型 RBAC 基于角色的访问控制是实施面向企业安全策略的一种有效的访问控制方式。 基本思想是,对系统操作的各种权限不是直接授予具体的用户,而是在用户集合与权限集合之间建立一个角色集合。每一种角色对应一组相应的权限。一旦用户被分配了适当…...

不是说嵌入式是风口吗,那为什么工作还那么难找?
最近确实有很多媒体、机构渲染嵌入式可以拿高薪,这在行业内也是事实,但前提是你有足够的竞争力,真的懂嵌入式。 时至今日,能做嵌入式程序开发的人其实相当常见,尤其是随着树莓派、Arduino等开发板的普及,甚…...

【二叉树】114. 二叉树展开为链表
114. 二叉树展开为链表 解题思路 后序遍历思路将root的左子树和右子树展平将root的右子树接到左子树下方 然后将整个左子树作为右子树 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* Tree…...

docker的安装与基础使用
一.docker简介 1)什么是docker Docker是一种用于构建、打包和运行应用程序的开源平台。它基于操作系统级虚拟化技术,可以将应用程序和其依赖的库、环境等资源打包到一个可移植的容器中,形成一个轻量级、独立的可执行单元。 开发者在本地编…...
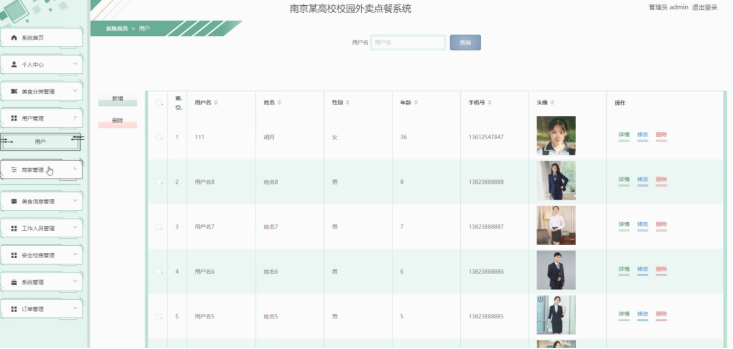
python+django+mysql高校校园外卖点餐系统--计算机毕设项目
本文的研究目标是以高校校园外卖点餐为对象,使其高校校园外卖点餐为目标,使得高校校园外卖点餐的信息化体系发展水平提高。论文的研究内容包括对个人中心、美食分类管理、用户管理、商家管理、美食信息管理、工作人员管理、安全检查管理、系统管理、订单…...

获取excel中的图片(包含wps中嵌入单元格图片)
项目中有excel导入功能,并且需要导入excel中的图片;模板如图: 已知office中插入的图片为浮动形式;如图: wps中可以插入浮动图片,也可以插入嵌入单元格图片;如图: 并且在wps嵌入单元格形式的图片可以看到使用的是公式;如图: 问题来了,如何获取图片 并且将图片与单元格进行对应 …...
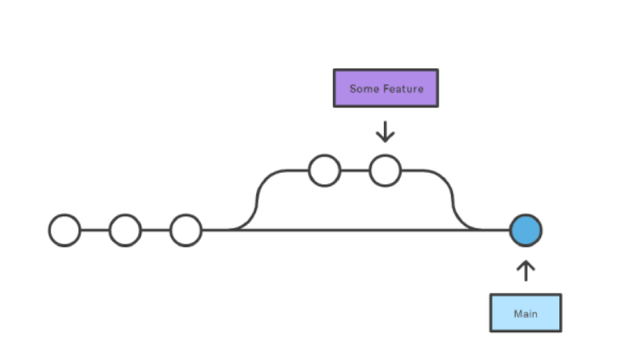
Git命令详解
1 常用命令 1)初始化本地仓库 git init <directory> 是可选的,如果不指定,将使用当前目录。 2)克隆一个远程仓库 git clone <url> 3)添加文件到暂存区 git add <file> 要添加当前目录中的所…...
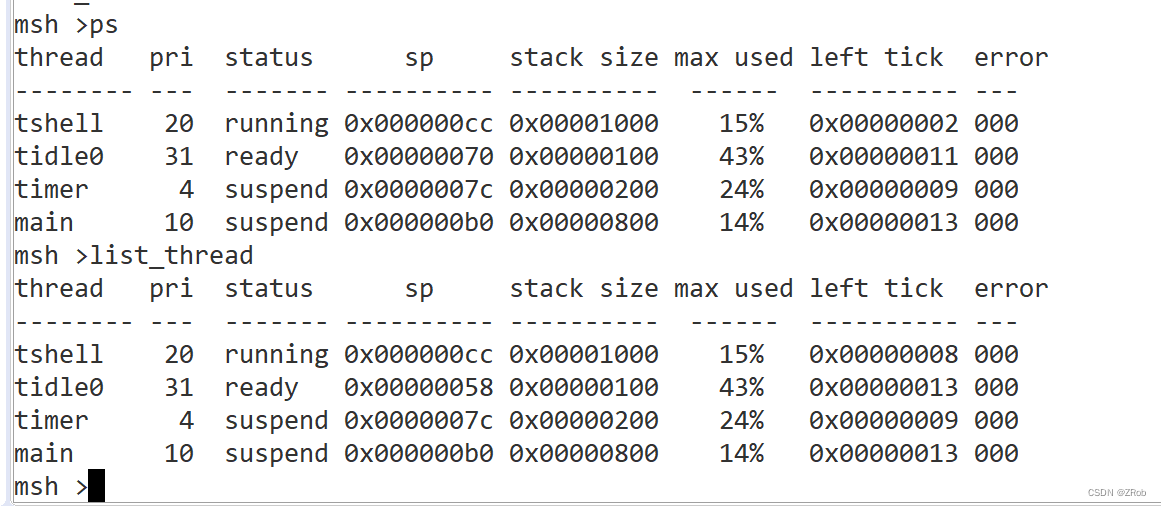
【STM32RT-Thread零基础入门】 4. 线程介绍(理论)
文章目录 前言一、线程的概念二、线程的调度三、上下文切换四、线程的重要属性1. 线程栈2. 线程的状态3. 线程优先级4. 线程时间片5. 线程的入口函数 五、RT-Thread命令查看系统线程信息总结 前言 前文中的最后一个任务发现,一个main()函数很难同时实现按键功能和闪…...

css学习3(三种样式表与样式控制优先级)
1、外部样式表:当样式需要应用于很多页面时,外部样式表将是理想的选择。在使用外部样式表的情况下,你可以通过改变一个文件来改变整个站点的外观。每个页面使用 <link> 标签链接到样式表,也要放到<head>中。 2、外部…...

【JS深层解析】内存
前言 接触过 C 语言的小伙伴应该了解:C语言拥有底层最原始的内存管理办法,例如:malloc() 和 free()方法,它们被开发者用来从操作系统中分配和释放内存。 然而在JavaScript这门语言中,当我们创建了一个东西(可以被读写、传递的数据),浏览器中的 js 引擎会根据创建这个…...
)
第二章:25+ Python 数据操作教程(第十四节NUMPY 教程与练习)
NumPy(“Numerical Python”或“Numeric Python”的缩写)是 Python 中对数组和矩阵进行快速数学计算的最基本的软件包之一。在处理多维数据时它也非常有用。集成C、C++和FORTRAN工具是一件幸事。它还提供了许多傅里叶变换 (FT) 和线性代数函数。 为什么使用 NumPy 而不是列…...
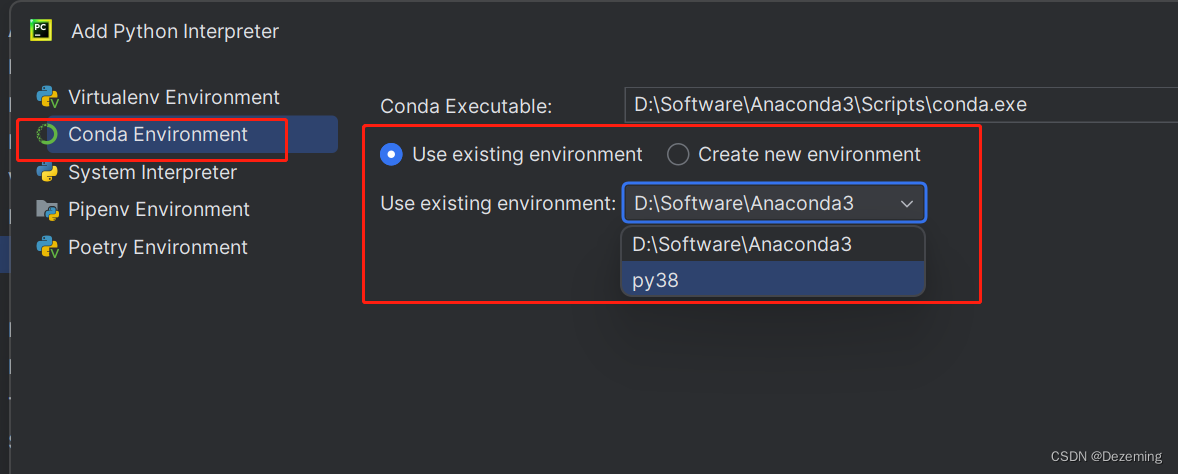
Pycharm与Anaconda Python的开发环境搭建
目录 一:下载 二:安装python 三:设置Pycharm 一:下载 下载Anaconda: Anaconda | The World’s Most Popular Data Science Platform 安装好以后,设置一下环境变量: 打开命令行,…...
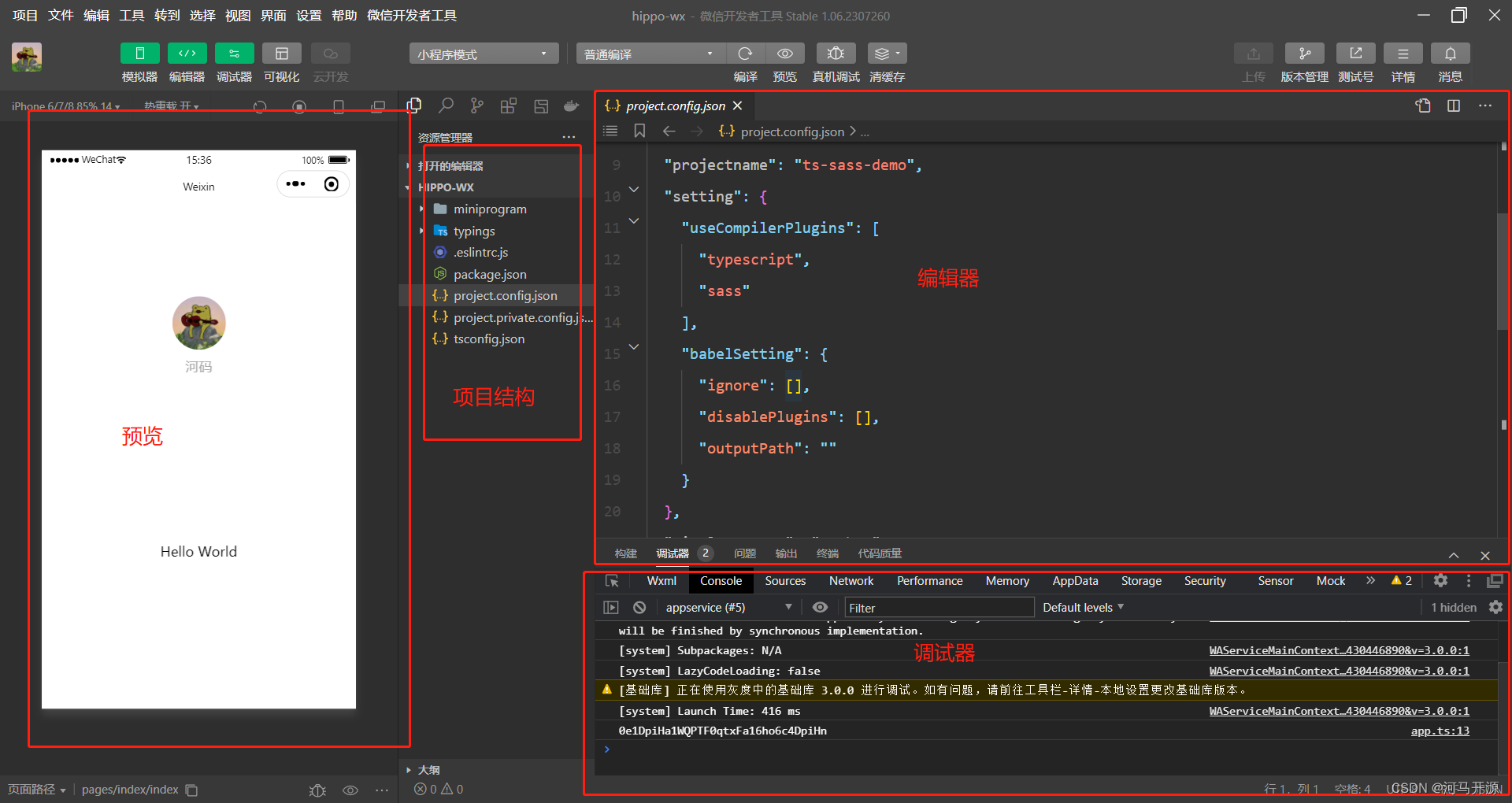
2.创建小程序
创建 在开发工具中,选择小程序,点击加号 填写小程序信息,模板使用的是TS+Sass 编辑器的工作区 目录结构 项目使用的是ts的模板,目录结构和js的有一点差异,目录结构如下: miniprogram:小程序根目录 —pages:小程序页面目录 ——xxx:页面目录,一个页面对应一个目…...
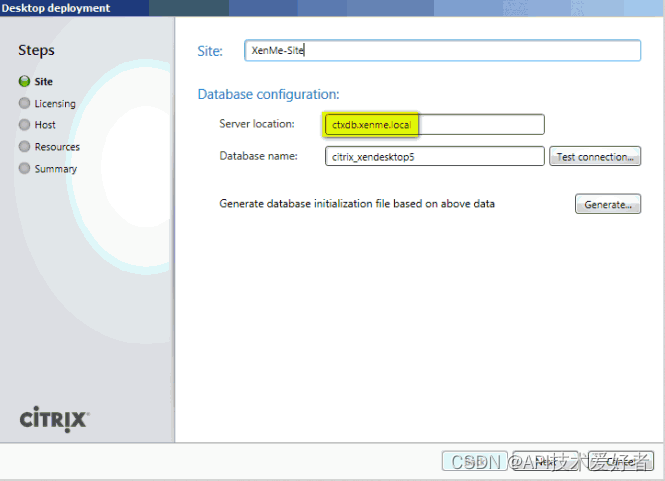
XenDesktop5.6如何连接数据库
Citrix在数据库的连接方式上一直不统一,但是也还是有迹可循的。 经过了好长时间的下载以后,今天终于有时间来测试一下最新版本的XenDesktop 5 SP1,由于结合了其他组件和环境的需要,所以,选择了独立部署数据库…...

OAuth2.0一 Spring Security OAuth2.0
这里主讲OAuth2.0 学习OAuth2前提: 掌握Spring Security Spring Security学习 一 OAuth2.0介绍 OAuth(Open Authorization)是一个关于授权(authorization)的开放网络标准,允许用户授权第三方应用访问他们…...

【linux】kernel编译时相关报错
文章目录 1. 问题现象及解决方式1. cc1: error: code model kernel does not support PIC mode 1. 问题现象及解决方式 1. cc1: error: code model kernel does not support PIC mode 问题:编译module时报错 原因:未指定交叉编译器,导致默认…...

C语言 功能型API --------------------strcat()
NAME strcat, strncat - concatenate two strings 头文件 SYNOPSIS #include <string.h> 函数原型: char *strcat(char *dest, const char *src); 功能: 在字符串dest的末尾将字符串src拼接上去 #include <stdio.h> #inc…...
企业展示小程序搭建指南
如今,移动互联网的快速发展,为企业展示提供了更多元化的方式。除了传统的宣传手段,企业还可以借助小程序来展示自己的实力和产品。本文将为大家介绍一种简单的DIY小程序的方法,让企业能够快速打造自己的展示平台。 首先࿰…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
