二分查找旋转数组
已知整数数组nums,先按升序排序后,再旋转。旋转k位后,元素分别为nums[k],nums[k+1]...nums[0]...nums[k-1]。请查找target 是否存在,如果存在返回所在索引;否则返回-1。假定nums没有重复的元素。
假定排序后的数组为{1,2,3,4,5}。
旋转0位:不变。
旋转1位:{2,3,4,5,1}
旋转2位:{3,4,5,1,2}
旋转3位:{4,5,1,2,3}
旋转4位:{5,1,2,3,4}
解题思路
观察后,可以得到如下结论:
旋转数组,可以拆分成左右两个升序数组,且左数组的任意元素都大于右数组的任意元素。
分两步:
- 找到数组的分界线RBegin,[0,RBegin)是左数组,[RBegin,n)是右数组。特殊情况:只有一个升序数组,则RBegin为0,左数组为空。
- 如果是小于等于nums.back(),在右边找;否则在左边找。升序寻找元素之前已经讲过了,就不累赘了。
-
-
-
-
- 寻找RBegin
-
-
-
-
| nums[mid] < nums.back() | 扔掉右边,不扔mid |
| nums[mid] == nums.back() | 扔掉右边,不扔mid |
| nums[mid] > nums.back() | 扔掉左边,扔掉mid |
故用左开右闭空间。
代码
class Solution {
public:
int search(vector<int>& nums, int target) {
int rBegin = FindRBegin(nums);
if (target <= nums.back())
{
return Find(nums, rBegin, nums.size(), target);
}
return Find(nums, 0, rBegin, target);
}
int FindRBegin(const vector<int>& nums)
{
int left = -1, r = nums.size()-1;//左开右闭
while (r - left > 1)
{
const int mid = left + (r - left) / 2;
if (nums[mid] <= nums.back())
{
r = mid;
}
else
{
left = mid;
}
}
return r;
}
int Find(const vector<int>& nums, int left, int r, int target)
{
while (r - left > 1)
{
const auto mid = left + (r - left) / 2;
if (nums[mid] <= target)
{
left = mid;
}
else
{
r = mid;
}
}
return (target == nums[left]) ? left : -1;
}
};
int main()
{
vector<int> vNums = {1,2,3,4,6};
auto res = Solution().search(vNums, 4);
std::cout << "index:" << res;
if (-1 != res)
{
std::cout << " value:" << vNums[res];
}
}
注意
开发及测试操作系统:Windows10(安装的时候没注意,安装成了英文版)
开发及测试环境:Microsoft Visual Studio 2022
如果还不明白,请看我的视频;如果看完视频,还是不明白,请下载源码后,直接修改。
相关文章:

二分查找旋转数组
已知整数数组nums,先按升序排序后,再旋转。旋转k位后,元素分别为nums[k],nums[k1]...nums[0]...nums[k-1]。请查找target 是否存在,如果存在返回所在索引;否则返回-1。假定nums没有重复的元素。 假定排序后的数组为{1…...

关于3D位姿旋转
一. 主动旋转和被动旋转 1. active rotation 主动旋转 站在坐标系的位置看旋转目标物:目标物主动发生旋转。 2. passive rotation 被动旋转 站在旋转目标物的位置看坐标系: 坐标系发生旋转,相当于目标物在坐标系内的位置被动地发生了旋转…...

解锁项目成功的关键:项目经理的结构化思维之道
1. 项目经理的核心职责 作为项目经理,我们的工作不仅仅是跟踪进度和管理团队。我们的角色在整个项目生命周期中都是至关重要的,从初始概念到最终交付。以下是项目经理的几个核心职责: 确保项目目标的清晰性项目的成功在很大程度上取决于其目…...

力扣974被K整除的子数组
同余定理 使用前缀和哈希表 由于可能是负数所以要进行修正:(sum%kk)%k class Solution { public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int> hash;hash[0 % k] 1; //0 这个数的余数int sum 0, ret 0;for(auto x…...

简单认识Docker数据管理
文章目录 为何需要docker数据管理数据管理类型 一、数据卷二、数据卷容器三、容器互联 为何需要docker数据管理 因为数据写入后如果停止了容器,再开启数据就会消失,使用数据管理的数据卷挂载,实现了数据的持久化,重启数据还会存在…...

UDP数据报结构分析(面试重点)
在传输层中有UDP和TCP两个重要的协议,下面将针对UDP数据报的结构进行分析 UDP结构图示 UDP报头结构的分析 UDP报头有4个属性,分别是源端口,目的端口,UDP报文长度,校验和,它们都占16位2个字节,所…...
【Java 动态数据统计图】动态数据统计思路案例(动态,排序,数组)二(113)
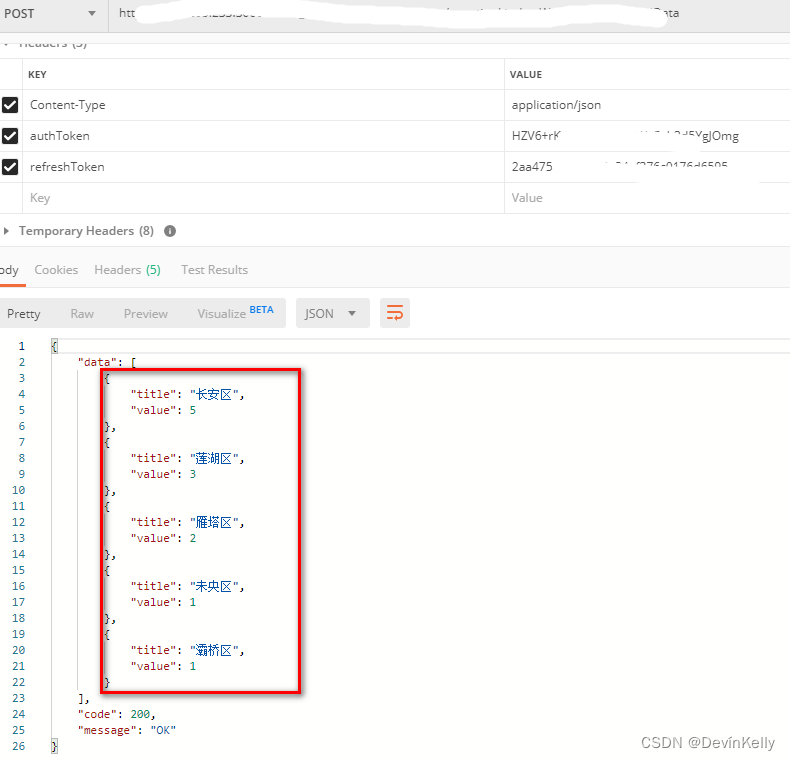
需求: 有一个List<Map<String.Object>>,存储了区域的数据, 数据是根据用户查询条件进行显示的;所以查询的数据是动态的;按区域维度统计每个区域出现的次数,并且按照次数的大小排序(升序&#…...
C++进阶 类型转换
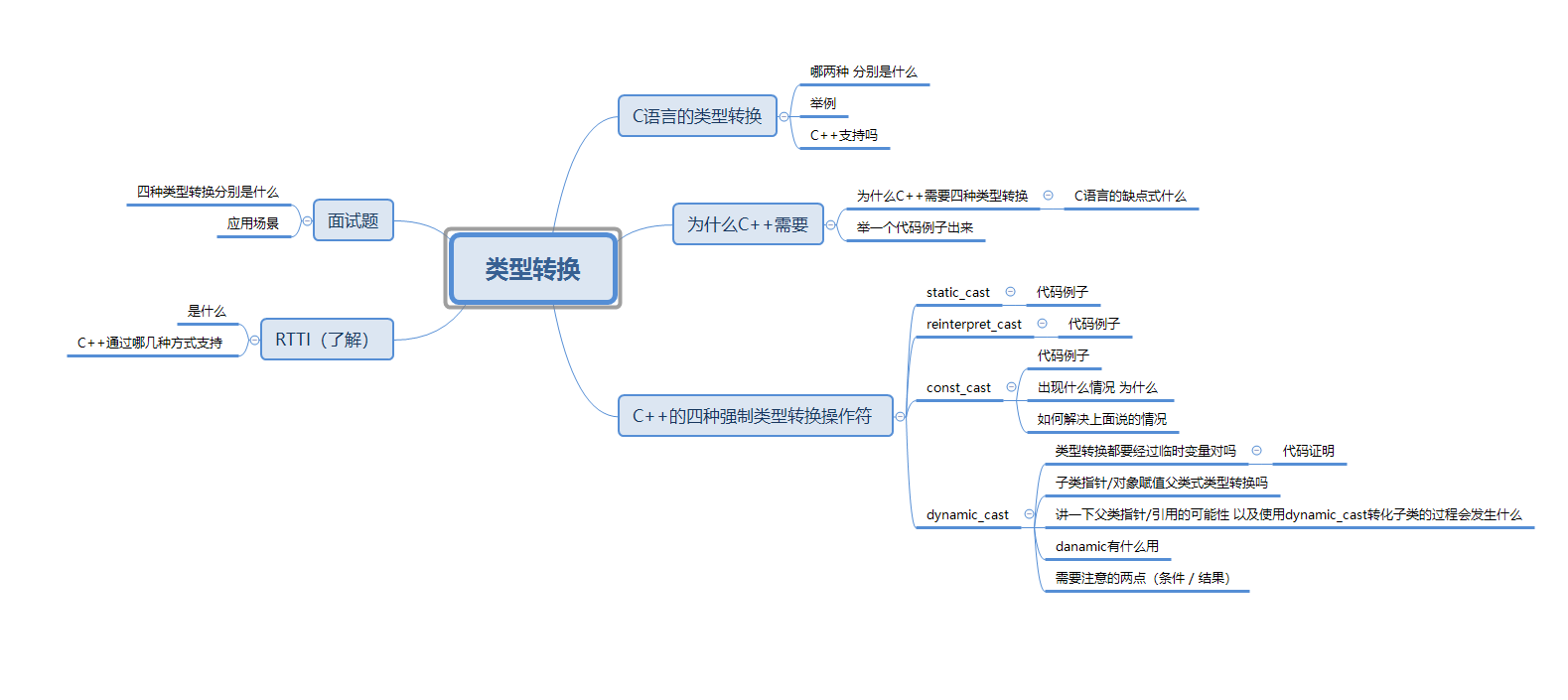
本文简介:介绍C中类型转换的方式 类型转换 C语言中的类型转换为什么C需要四种类型转换C强制类型转换static_castreinterpret_castconst_castdynamic_cast RTTI(了解)总结 C语言中的类型转换 在C语言中,如果赋值运算符左右两侧类型…...
Idea中隐藏指定文件或指定类型文件
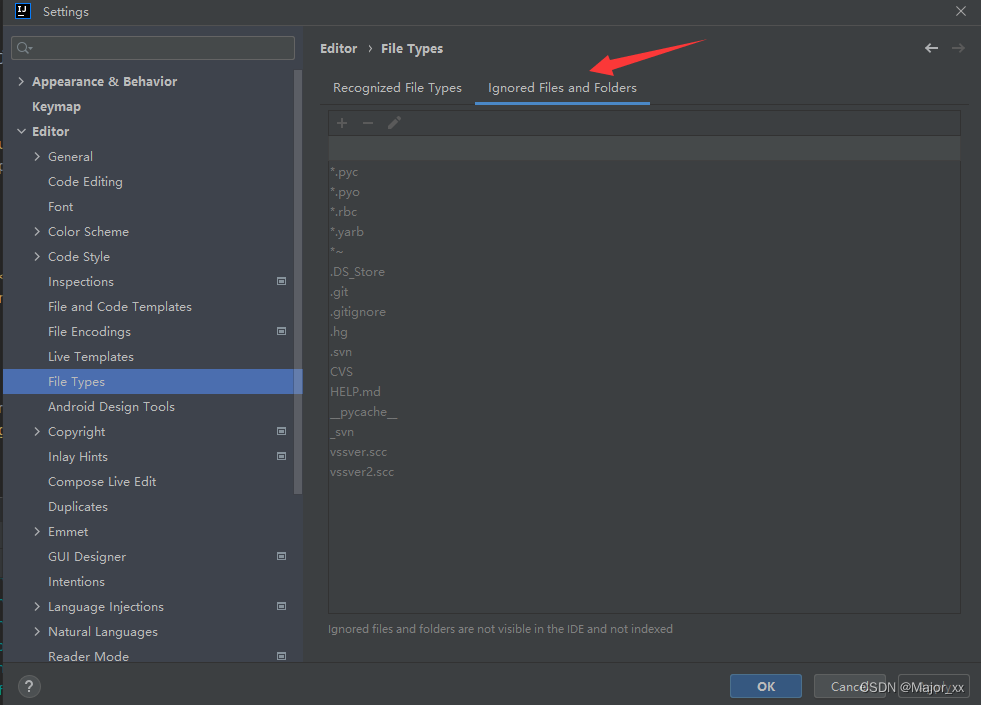
Setting ->Editor ->Code Style->File Types → Ignored Files and Folders输入要隐藏的文件名,支持*号通配符回车确认添加...

第2步---MySQL卸载和图形化工具展示
第2步---MySQL卸载和图形化工具展示 1.MySQL的卸载 2.MySQL的图形化工具 2.1常见的图形化工具 SQLyog:简单。SQLyog首页、文档和下载 - MySQL 客户端工具 - OSCHINA - 中文开源技术交流社区 Mysql Workbench :MySQL :: MySQL Workbench DataGrip&…...

原型和原型链
好久没记了有点忘记了,来记录一下。 1、函数和对象的关系:对象都是通过函数创建的,函数也是一个对象。 2、原型和原型链 1.原型:原型分为两种 prototype:每一个函数都会有prototype属性,它指向函数的原型…...
解决ios隔空播放音频到macos没有声音的问题
解决ios隔空播放音频到macos没有声音的问题 一、检查隔空播放支持设备和系统要求二、打开隔空播放接收器三、重置MAC控制中心进程END 一、检查隔空播放支持设备和系统要求 Mac、iPhone、iPad 和 Apple Watch 上“连续互通”的系统要求 二、打开隔空播放接收器 ps;我设备是同一…...
LTPP在线开发平台【使用教程】
LTPP在线开发平台 点击访问 LTPP在线开发平台 LTPP(Learning teaching practice platform)在线开发平台是一个编程学习网站,该网站集文章学习、短视频、在线直播、代码训练、在线问答、在线聊天和在线商店于一体,专注于提升用户编…...

0818 新增码表 git拉取代码
目的是新增两个码表字段。然后和前端联调。 use db; delete from sys_dict_data where dict_type res_switch_status; INSERT INTO sys_dict_data VALUES (0, 1, 已接入, 1, res_switch_status, NULL, default, N, 0, , 2022-07-26 10:43:41, , NULL, NULL); INSERT INTO sys…...

AI 绘画Stable Diffusion 研究(十)sd图生图功能详解-精美二维码的制作
免责声明: 本案例所用安装包免费提供,无任何盈利目的。 大家好,我是风雨无阻。 为了让大家更直观的了解图生图功能,明白图生图功能到底是干嘛的,能做什么事情?今天我们继续介绍图生图的实用案例-精美二维码的制作。 对…...
报错)
C# File.ReadAllLines()报错
项目中需要读取一个文本文件的内容,调用C#的File.ReadAllLines(path)方法,但是报错,就提示unknown exception,也没其他提示了。 文件是在的,并且,如果把文件拷贝到另外一个路径,再次读取是正常…...
LeetCode 1162. As Far from Land as Possible【多源BFS】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

【算法】二分查找(整数二分和浮点数二分)
二分查找也称折半查找(Binary Search),是一种效率较高的查找方法,时间复杂度为O(logN)。 二分查找采用了“分治”策略。使用二分查找时,数组中的元素之间得有单调性(升序或者降序)。 二分的模…...
git压缩/合并多次commit提交为1次commit提交
git压缩/合并N次commit提交为1次commit提交 假设有最近3次提交: commit_id1 commit_id2 commit_id3目标是把以上3次commit合并成1个commit,注意,最新的commit提交在最上面。 在git bash里面的操作步骤: (1࿰…...
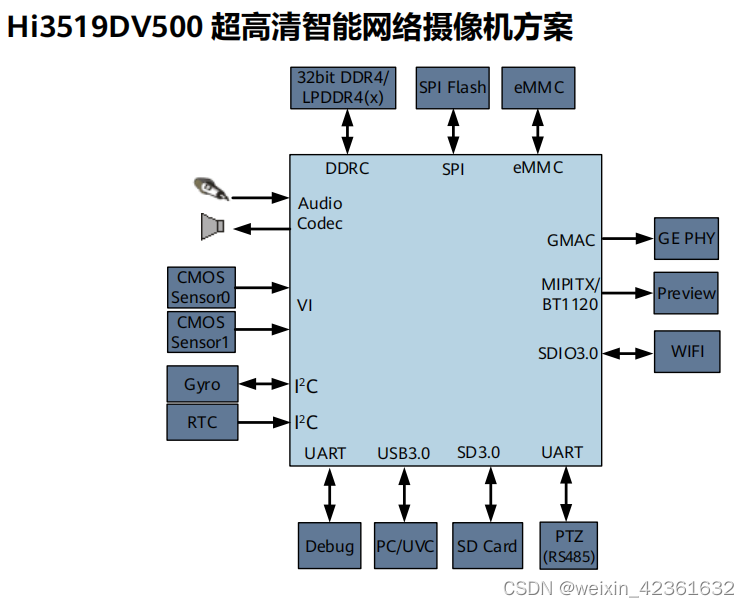
【3519DV500】AI算法承载硬件平台_2.5T算力+AI ISP图像处理_超感光视频硬件方案开发
Hi3519DV500 内置双核 A55 ,提供高效、丰富和灵活的CPU 资源,以满足客户计算和控制需求。 Hi3519DV500集成了高效的神经网络推理引擎,最高2.5Tops NN算力,支持业界主流的神经 网络框架。神经网络支持完整的 API 和工具链…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
