LA@n维向量@解析几何向量和线性代数向量
文章目录
- 概念
- n维向量
- 向量类型
- 实向量和复向量
- 行向量和列向量
- 行列向量的转换
- 特殊向量
- 向量运算
- 矩阵的向量分块👺
- 解析几何向量和线性代数向量👺
概念
n维向量
- 由 n n n个有次序的数 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an组成的有序数组称为n维向量,简称向量
- 数 a i a_i ai称为向量的第 i i i个分量
向量类型
实向量和复向量
- 分量全为实数的向量称为实向量,分量是复数的向量称为复向量(实向量是从属于复向量的)
- 这里默认讨论的是实向量
行向量和列向量
-
n n n维向量可以写成一行或一列,分别称为行向量,列向量(或分别称为行矩阵,列矩阵)
-
一个 n n n维行向量是 1 × n 1\times{n} 1×n的矩阵
- ( a 1 a 2 ⋮ a n ) \begin{pmatrix} a_1\\a_2\\\vdots\\a_n \end{pmatrix} a1a2⋮an
-
一个 n n n维列向量是 n × 1 n\times{1} n×1的矩阵
- ( a 1 a 2 ⋯ a n ) \begin{pmatrix}a_1&a_2&\cdots&a_n\end{pmatrix} (a1a2⋯an)
-
-
通常以小写希腊字母,例如: α , β , γ , ⋯ \boldsymbol{\alpha,\beta,\gamma,\cdots} α,β,γ,⋯表示向量
-
也可以用小写的粗体的英文字母表示,例如: a , b , ⋯ \boldsymbol{a,b,\cdots} a,b,⋯,或粗正体 a , b , ⋯ \bold{a,b,\cdots} a,b,⋯
-
有时为例书写方便,可以用非粗体: α , β , γ , ⋯ {\alpha,\beta,\gamma,\cdots} α,β,γ,⋯
-
在按行分块和按列分块的分块矩阵中,还可能出现用大写英文字母表示列分块或行分块,例如 A 1 , A 2 , ⋯ A_1,A_2,\cdots A1,A2,⋯
行列向量的转换
-
列向量可以看作行向量的转置
-
习惯上,向量通常默认指列向量,设向量包含 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an元素
-
列向量和行向量分别表示为
-
a = ( a 1 a 2 ⋮ a n ) = ( a 1 a 2 ⋯ a n ) T a T = ( a 1 a 2 ⋯ a n ) = ( a 1 , a 2 , ⋯ , a n ) \bold{a}=\begin{pmatrix} a_1\\a_2\\\vdots\\a_n \end{pmatrix} =\begin{pmatrix}a_1&a_2&\cdots&a_n\end{pmatrix}^T \\ \bold{a}^T=\begin{pmatrix}a_1&a_2&\cdots&a_n\end{pmatrix}=(a_1,a_2,\cdots,a_n) a= a1a2⋮an =(a1a2⋯an)TaT=(a1a2⋯an)=(a1,a2,⋯,an)
-
为了便于区分符号(文字)所表示的向量是列向量还是行向量,习惯上表示行向量的符号带上一个 T ^T T上标,例如 a T \bold{a}^T aT表示列向量 a \bold{a} a的转置得到的
-
简化书写,由于列向量如果严格竖着写比较占用空间,紧凑性不好,我们可以利用转置性质: a = ( a T ) T \bold{a}=(\bold{a}^T)^T a=(aT)T,将列向量用行向量的转置形式书写展开式,这样行列向量也可以用横着写
-
特殊向量
- 分量全为0的向量称为零向量
- 零向量第 i i i个分量改为1得到的向量是 a i = 1 a_i=1 ai=1的 n n n维基向量
向量运算
-
向量作为一种特殊的矩阵,仍然按照矩阵的运算规则运算
-
k a = k ( a 1 , a 2 , ⋯ , a n ) = ( k a 1 , k a 2 , ⋯ , k a n ) k\bold{a}=k(a_1,a_2,\cdots,a_n)=(ka_1,ka_2,\cdots,ka_n) ka=k(a1,a2,⋯,an)=(ka1,ka2,⋯,kan)
- − a = − ( a 1 , a 2 , ⋯ , a n ) = ( − a 1 , − a 2 , ⋯ , − a n ) -\bold{a}=-(a_1,a_2,\cdots,a_n)=(-a_1,-a_2,\cdots,-a_n) −a=−(a1,a2,⋯,an)=(−a1,−a2,⋯,−an)为向量 − a -\bold{a} −a的负向量
矩阵的向量分块👺
-
A = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ) A=\begin{pmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots & &\vdots \\ a_{m1} &a_{m2} &\cdots &a_{mn} \\ \end{pmatrix} A= a11a21⋮am1a12a22⋮am2⋯⋯⋯a1na2n⋮amn
-
记 α j = ( a 1 j a 2 j ⋮ a m j ) , j = 1 , 2 , ⋯ , n A = ( α 1 α 2 ⋯ α n ) \\记\alpha_j =\begin{pmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{mj} \\ \end{pmatrix},j=1,2,\cdots,n \\A=\begin{pmatrix} \alpha_{1}&\alpha_{2}&\cdots&\alpha_{n} \\ \end{pmatrix} 记αj= a1ja2j⋮amj ,j=1,2,⋯,nA=(α1α2⋯αn)
-
记 β i T = ( a i 1 , a i 2 , ⋯ , a i n ) , i = 1 , 2 , ⋯ , m A = ( β 1 T β 2 T ⋮ β m T ) 记\beta_i^T=(a_{i1},a_{i2},\cdots,a_{in}),i=1,2,\cdots,m \\ A= \begin{pmatrix} \beta_{1}^T\\ \beta_{2}^T\\ \vdots \\ \beta_{m}^T \\ \end{pmatrix} 记βiT=(ai1,ai2,⋯,ain),i=1,2,⋯,mA= β1Tβ2T⋮βmT
-
A = ( α 1 α 2 ⋯ α n ) = ( β 1 T β 2 T ⋮ β m T ) A=\begin{pmatrix} \alpha_{1}&\alpha_{2}&\cdots&\alpha_{n} \\ \end{pmatrix} =\begin{pmatrix} \beta_{1}^T\\ \beta_{2}^T\\ \vdots \\ \beta_{m}^T \\ \end{pmatrix} A=(α1α2⋯αn)= β1Tβ2T⋮βmT
解析几何向量和线性代数向量👺
- 在解析几何中,我们把"既有大小又有方向的量"叫做向量
- 把可随意平移的有向线段作为向量的几何形象
- 引进坐标系后,这种向量就有了坐标表示: n n n个有次序的实数数组 ( a 1 , ⋯ , a n ) (a_1,\cdots,a_n) (a1,⋯,an)
- n = 1 n=1 n=1对应的是标量
- n = 2 n=2 n=2对应于二维平面向量
- n = 3 n=3 n=3对应于三维空间向量
- 当 n ⩽ 3 n\leqslant{3} n⩽3时, n n n维向量可以把有向线段作为几何形象
- 当 n > 3 n>3 n>3时, n n n维向量不再有几何形象,但是沿用一些几何术语
向量空间
- 几何中,"空间"通常是作为点的集合,构成空间的元素是点,这样的空间叫做点空间
- 我们把 3 3 3维向量的全体所组成的集合: R 3 \mathbb{R}^3 R3={ r = ( x , y , z ) T ∣ x , y , z ∈ R \bold{r}=(x,y,z)^T|x,y,z\in\mathbb{R} r=(x,y,z)T∣x,y,z∈R}称为3维向量空间
- 在点空间取定坐标系后,三维空间中的点 P ( x , y , z ) P(x,y,z) P(x,y,z)与 3 3 3维向量 r = ( x , y , z ) T \bold{r}=(x,y,z)^T r=(x,y,z)T之间有一 一对应关系
- 因此向量空间可以类比为"取定了坐标系"的点空间
- 在讨论向量的运算时,我们把向量看作有向线段
- 在讨论向量集时,把向量 r \bold{r} r看作时 r \bold{r} r为径向的点 P P P,从而把点 P P P的轨迹作为向量集作为向量集的图形
- 例如 Π = { P ( x , y , z ) ∣ a x + b y + c z + d = 0 } \Pi=\{P(x,y,z)|ax+by+cz+d=0\} Π={P(x,y,z)∣ax+by+cz+d=0},结合空间解析几何的知识,是一个平面方程的一般式,因此 Π \Pi Π是一个平面 ( a 2 + b 2 + c 2 > 0 ) (a^2+b^2+c^2>{0}) (a2+b2+c2>0)或 ( a , b , c ) ≠ ( 0 , 0 , 0 ) (a,b,c)\neq{(0,0,0)} (a,b,c)=(0,0,0)
- 由此,向量集 S = { r = ( x , y , z ) T ∣ a x + b y + c z + d = 0 } S=\{\bold{r}=(x,y,z)^T|ax+by+cz+d=0\} S={r=(x,y,z)T∣ax+by+cz+d=0}也叫做向量空间 R 3 \mathbb{R}^3 R3中的平面(3维空间中的2维平面),并把 Π \Pi Π作为向量集S的图形
- 将 x , y , z x,y,z x,y,z替换为 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3; x , y , z x,y,z x,y,z替换为 a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3,则平面方程作 ( ∑ i = 1 3 a i x i ) + b = 0 (\sum_{i=1}^{3}a_ix_i)+b=0 (∑i=13aixi)+b=0
n n n维向量空间
- 设集合 D = { 1 , 2 , ⋯ , n } D=\{1,2,\cdots,n\} D={1,2,⋯,n}
- n n n维向量的全体构成的集合 R 3 \mathbb{R}^3 R3={ x = ( x 1 , x 2 , ⋯ , x n ) T ∣ ∀ i ∈ D , x i ∈ R \bold{x}=(x_1,x_2,\cdots,x_n)^T|\forall{i}\in{D},x_i\in\mathbb{R} x=(x1,x2,⋯,xn)T∣∀i∈D,xi∈R}叫做 n n n维向量空间
n n n维空间的 n − 1 n-1 n−1维超平面
- n n n维向量的集合{ x = ( x 1 , x 2 , ⋯ , x n ) T ∣ ( ∑ i = 1 n a i x i ) + b = 0 \bold{x}=(x_1,x_2,\cdots,x_n)^T|(\sum_{i=1}^{n}a_ix_i)+b=0 x=(x1,x2,⋯,xn)T∣(∑i=1naixi)+b=0}叫做 n n n维向量空间 R n \mathbb{R}^n Rn中的 n − 1 n-1 n−1维超平面
相关文章:

LA@n维向量@解析几何向量和线性代数向量
文章目录 概念n维向量向量类型实向量和复向量行向量和列向量行列向量的转换特殊向量向量运算 矩阵的向量分块👺 解析几何向量和线性代数向量👺向量空间 n n n维向量空间 n n n维空间的 n − 1 n-1 n−1维超平面 概念 n维向量 由 n n n个有次序的数 a …...
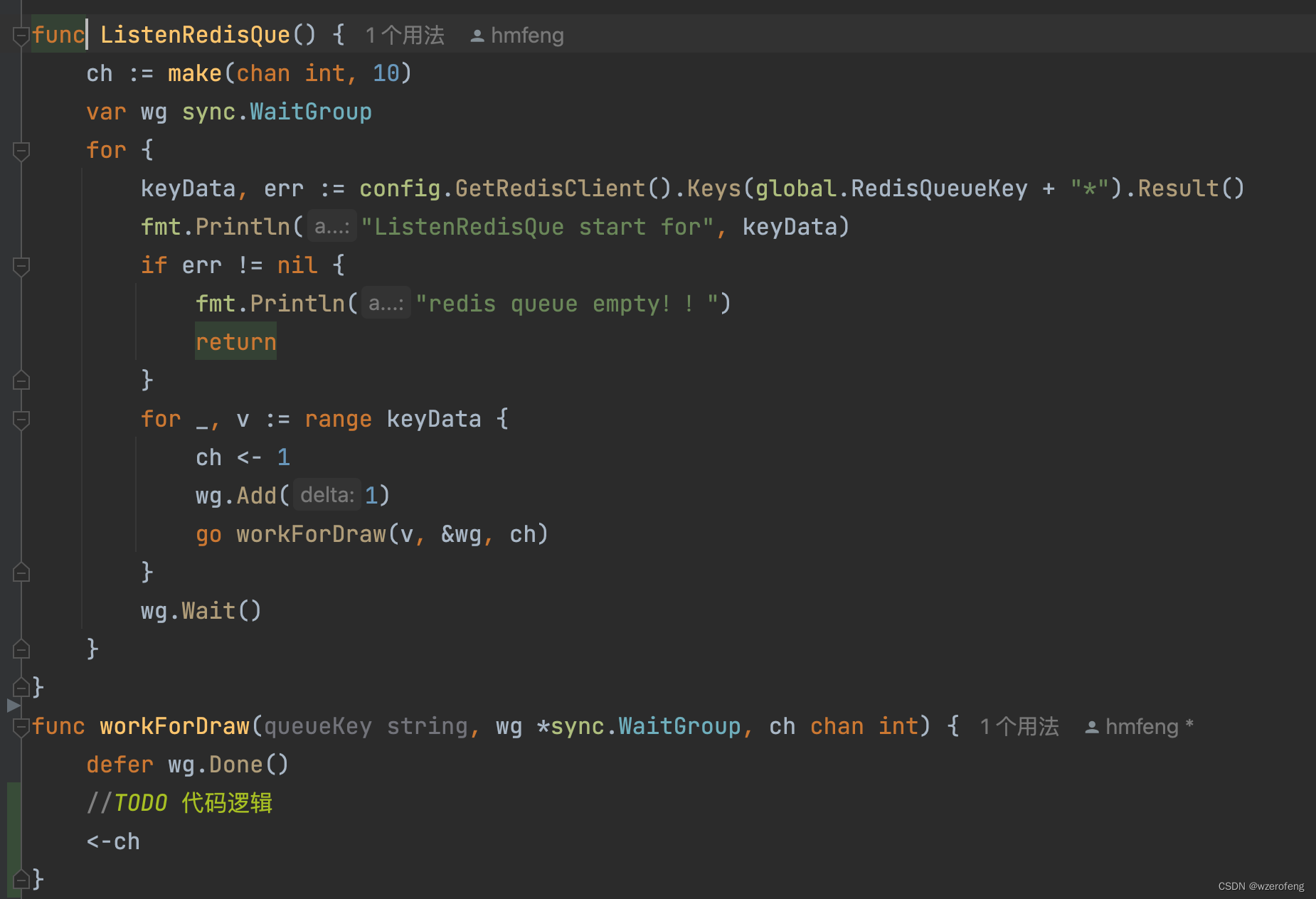
go 协程并发数控制
错误的写法: 这里的<-ch 是为了从channel 中读取 数据,为了不使channel通道被写满,阻塞 go 协程数的创建。但是请注意,go workForDraw(v, &wg) 是不阻塞后续的<-ch 执行的,所以就一直go workForDraw(v, &…...
MySQL的安装以及卸载
下载官网 https://www.mysql.com/ 切到下载tab页 找到 MySQL Community Server 或者 MySQL Community (GPL) Downloads --> MySQL Community Server 点击download按钮: 点击download进入下载页面选择No thanks, just start my download就可以开始下载了。 下…...

LRU算法与Caffeine、Redis中的缓存淘汰策略
推荐阅读 AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI绘画、AI讲话、翻译,GPU点亮AI想象空间 资源分享 「java、python面试题」来自UC网盘app分享,打开手机app,额外获得1T空间 https://dr…...

HTML笔记(3)
表单标签 用于登录、注册界面,以采集用户输入的信息,把信息采集到之后,用户一点按钮,就会把这些信息发送到服务端,服务端就可以把这些数据存储到数据库,所以表单是一个非常重要的html标签,它主要…...
,实际上对应的就是虚函数)
c++——重写(覆盖),实际上对应的就是虚函数
重写是指派生类中存在重新定义的函数。其函数名,参数列表,返回值类型,所有都必须同基类中被重写的函数一致。只有函数体不同(花括号内),派生类调用时会调用派生类的重写函数,不会调用被重写函数…...
算法通关村——字符串反转问题解析
1. 反转字符串 反转字符串 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。 不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。 1.1 交换 这一题的思路还是简单的&…...
,点击关闭按钮按钮重置tree)
vue + elementui 中 在弹框中使用了 tree型结构(<el-tree></el-tree>),点击关闭按钮按钮重置tree
vue 项目中使用了element-ui 中 tree,选择了懒加载的模式 通过点击按钮,使得 tree 重新加载 <div class"head-container header-tree" v-if"addDialogVisible"><el-treeref"tree":data"treeData":loa…...

windows adb根据id点击按钮
在 Windows 上使用 adb 根据控件的 ID 来模拟点击按钮,可以使用以下命令: 查看当前屏幕上的所有控件信息,并将其保存到文件中: adb shell uiautomator dump /sdcard/ui.xml 将设备上的 ui.xml 文件下载到计算机上: ad…...
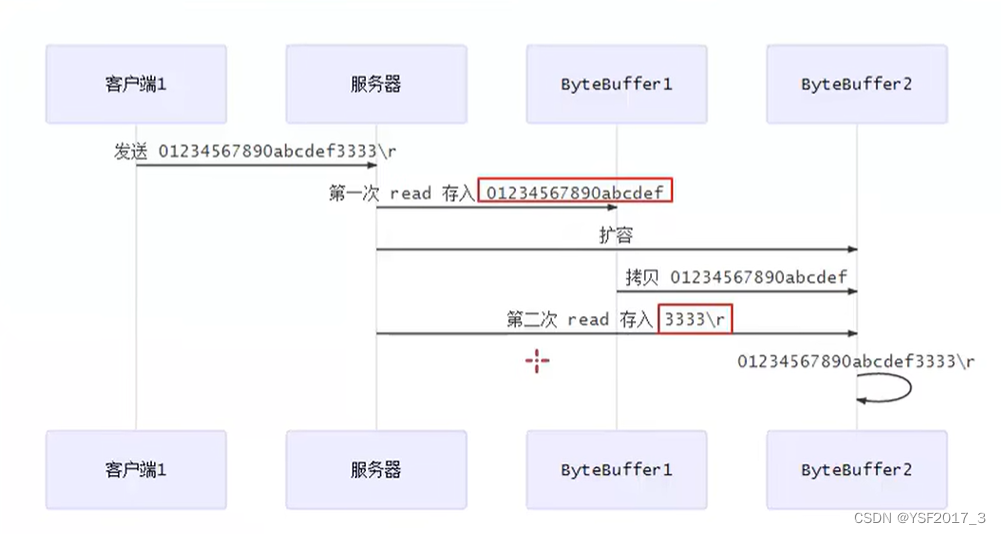
netty(一):NIO——处理消息边界
处理消息边界 为什么要处理边界 因为会存在半包和粘包的问题 1.客户端和服务端约定一个固定长度 优点:简单 缺点:可能造成浪费 2.客户端与服务端约定一个固定分割符 *缺点 效率低 3.先发送长度,再发送数据 TLV格式: type…...

等保测评--安全计算环境--测评方法
安全子类--身份鉴别 a)应对登录的用户进行身份标识和鉴别,身份标识具有唯一性,身份鉴别信息具有复杂度要求并定期更换; 一、测评对象 终端和服务器等设备中的操作系统(包括宿主机和虚拟机操作系统) 、网络设备(包括虚拟网络设备)、安全设备(包括虚拟安全设备)、移动终端…...
色彩空间和通道)
open cv学习 (二)色彩空间和通道
色彩空间和通道 demo1 import cv2hsv_image cv2.imread("./img.png")cv2.imshow("img", hsv_image) hsv_image cv2.cvtColor(hsv_image, cv2.COLOR_BGR2HSV) h, s, v cv2.split(hsv_image) cv2.imshow("B", h) cv2.imshow("G", s…...
RS232、RS422、RS485硬件及RS指令、RS2指令应用知识学习
RS232、RS422、RS485硬件及RS指令、RS2指令应用知识学习 一、串行(异步/同步)通讯、并行通讯、以太网通讯 二、单工通讯/半双工通讯/双工通讯 三、常用硬件接口(工业上基本是RS485两线制的接线) 常用硬件接口RS232/RS422/RS485,…...

背景属性样式
🍓背景属性 属性名称中文注释备注background-image背景图片url(img-path)background-color背景颜色background-attachment设置背景固定scroll默认值,随盒子滚动, fixed固定,脱离标准流,固定在浏览器窗口,当…...
)
蓝桥杯每日N题 (消灭老鼠)
大家好 我是寸铁 希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 不清楚蓝桥杯考什么的点点下方👇 考点秘籍 想背纯享模版的伙伴们点点下方👇 蓝桥杯省一你一定不能错过的模板大全(第一期) 蓝桥杯省一你一定不…...

k8s 用户角色 权限的划分
在Kubernetes中,角色(Role)和角色绑定(RoleBinding)用于划分用户的权限。 Kubernetes中的角色定义了一组特定操作的权限,例如 创建、删除或修改特定资源。而 角色绑定则将角色与用户、组或服务账号进行关联…...

聊一下操作系统 macOS 与 Linux
对于Windows操作系统大家都比较熟悉,也常拿它与Linux操作系统进行比较,两者之间的差异也很明显。但对于macOS 和 Linux的比较不太多,很多人认为它们很相似,因为这两种操作系统都可以运行 Unix 命令。其实详细比较下,两…...

OJ练习第153题——分发糖果
分发糖果 力扣链接:135. 分发糖果 题目描述 n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。 你需要按照以下要求,给这些孩子分发糖果: 每个孩子至少分配到 1 个糖果。 相邻两个孩子评分更高的孩子会获得更多的糖果。…...

iOS 通知推送服务端部署测试过程详细版
文章目录 iOS 通知推送服务端部署测试过程详细版前言部署Serverless 版Bark-server1.注册Render 账号2.创建一个Web Service3.连接 repository4.Web Service 设置推送测试1.手机端安装 bark2.设定服务器3.发送测试推送请求参数列表:4.手机推送结果iOS 通知推送服务端部署测试过…...

【COMP282 LEC3 LEC4 LEC5】
LEC 3 Overloading 超载 1. Two functions can have the same name if they have different parameters 2. The compiler will use the one whose parameters match the ones you pass in Performing Addition “” 重载一个operator ,这个operator函数被定义…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
