Practices11|41. 缺失的第一个正数(数组)、73. 矩阵置零(矩阵)
41. 缺失的第一个正数(数组)
1.题目:
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0] 输出:3
示例 2:
输入:nums = [3,4,-1,1] 输出:2
示例 3:
输入:nums = [7,8,9,11,12] 输出:1
提示:
1 <= nums.length <= 5 * 105-231 <= nums[i] <= 231 - 1
2.思路:
如果本题没有额外的时空复杂度要求,那么就很容易实现:
可以将数组所有的数放入哈希表,随后从 111 开始依次枚举正整数,并判断其是否在哈希表中;
我们可以从 1开始依次枚举正整数,并遍历数组,判断其是否在数组中。
如果数组的长度为 NNN,那么第一种做法的时间复杂度为 O(N),空间复杂度为 O(N);第二种做法的时间复杂度为O(N^2),空间复杂度为 O(1)。但它们都不满足时间复杂度为 O(N) 且空间复杂度为 O(1)。
「真正」满足时间复杂度为 O(N) 且空间复杂度为 O(1)的算法是不存在的,但是我们可以退而求其次:利用给定数组中的空间来存储一些状态。也就是说,如果题目给定的数组是不可修改的,那么就不存在满足时空复杂度要求的算法;但如果我们可以修改给定的数组,那么是存在满足要求的算法的。
方法一:哈希表
第一种做法:
我们可以将数组所有的数放入哈希表,随后从 1开始依次枚举正整数,并判断其是否在哈希表中。仔细想一想,我们为什么要使用哈希表?这是因为哈希表是一个可以支持快速查找的数据结构:给定一个元素,我们可以在 O(1) 的时间查找该元素是否在哈希表中。因此,我们可以考虑将给定的数组设计成哈希表的「替代产品」。
实际上,对于一个长度为 N 的数组,其中没有出现的最小正整数只能在 [1,N+1] 中。这是因为如果 [1,N]都出现了,那么答案是 N+1,否则答案是 [1,N]中没有出现的最小正整数。这样一来,我们将所有在 [1,N] 范围内的数放入哈希表,也可以得到最终的答案。而给定的数组恰好长度为 N,有了一种将数组设计成哈希表的思路:
对数组进行遍历,对于遍历到的数 x,如果它在 [1,N]的范围内,那么就将数组中的第 x−1个位置(注意:数组下标从 0开始)打上「标记」。在遍历结束之后,如果所有的位置都被打上了标记,那么答案是 N+1,否则答案是最小的没有打上标记的位置加 1。
那么如何设计这个「标记」呢?由于数组中的数没有任何限制,因此这并不是一件容易的事情。但我们可以继续利用上面的提到的性质:由于我们只在意 [1,N]中的数,因此我们可以先对数组进行遍历,把不在 [1,N]范围内的数修改成任意一个大于 N的数(例如 N+1)。这样一来,数组中的所有数就都是正数了,因此我们就可以将「标记」表示为「负号」。算法的流程如下:
我们将数组中所有小于等于 0 的数修改为 N+1;
我们遍历数组中的每一个数 x,它可能已经被打了标记,因此原本对应的数为 ∣x∣,如果 ∣x∣∈[1,N],那么我们给数组中的第 ∣x∣−1个位置的数添加一个负号。注意如果它已经有负号,不需要重复添加;
在遍历完成之后,如果数组中的每一个数都是负数,那么答案是 N+1,否则答案是第一个正数的位置加 1。
3.代码:
class Solution {public int firstMissingPositive(int[] nums) {//将数字中小于等于0的数改为 N+1for(int i=0;i<nums.length;i++){if(nums[i]<=0){nums[i]=nums.length+1;}}//遍历数组中的每一个数,它可能已经被打了标记,因此绝对值//如果在长度范围内,那给数组中的第 ∣x∣−1个位置的数添加一个负号for(int i=0;i<nums.length;i++){int num=Math.abs(nums[i]);if(num<=nums.length){nums[num-1]=-Math.abs(nums[num-1]);}}//遍历完成后如果其中每一个数都是负数,那么答案是n+1,否则答案是第一个正数位置加1.for(int i=0;i<nums.length;i++){if(nums[i]>0){return i+1;}}return nums.length+1;}73. 矩阵置零
1.题目:
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
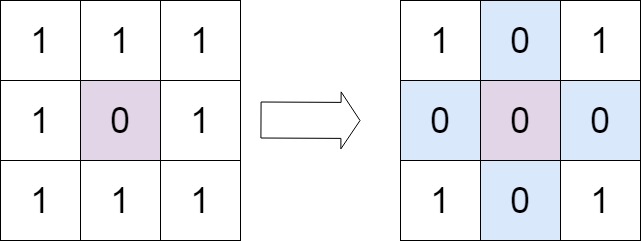
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
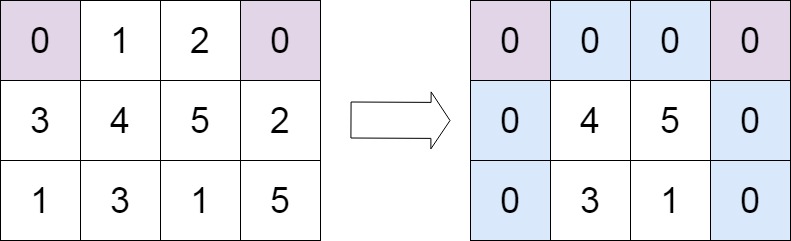
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
2.思路:
//用两个标记数组记录是否有0出现,出现了将标记数组改为true,再遍历一遍寻找标记的位置
//将原数组位置被标记的元素替换为0;
3.代码:
class Solution {public void setZeroes(int[][] matrix) {//用两个标记数组记录是否有0出现,出现了将标记数组改为true,再遍历一遍寻找标记的位置//将原数组位置被标记的元素替换为0;int m=matrix.length,n=matrix[0].length;boolean[] row=new boolean[m];boolean[] col=new boolean[n];for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(matrix[i][j]==0){row[i]=true;col[j]=true;}}}for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(row[i]||col[j]){matrix[i][j]=0;}}}}
}相关文章:

Practices11|41. 缺失的第一个正数(数组)、73. 矩阵置零(矩阵)
41. 缺失的第一个正数(数组) 1.题目: 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 示例 1: 输入:nums [1,2,0] 输出…...

深入完整的带你了解java对象的比较
目录 元素的比较 1.基本类型的比较 2.对象比较的问题 1.运行结果 2.疑问 3.原因 对象的比较 1.覆写基类的equals 2.基于Comparble接口类的比较 3.基于比较器比较 4.三种方式对比 元素的比较 1.基本类型的比较 在Java 中,基本类型的对象可以直接比较大…...

ubuntu20.04升级GLIBC高版本方法,解决:version `GLIBC_2.34‘ not found
检查版本 strings /lib/x86_64-linux-gnu/libc.so.6 |grep GLIBC_ 1 显示结果 GLIBC_2.2.5 GLIBC_2.2.6 GLIBC_2.3 GLIBC_2.3.2 GLIBC_2.3.3 GLIBC_2.3.4 GLIBC_2.4 GLIBC_2.5 GLIBC_2.6 GLIBC_2.7 GLIBC_2.8 GLIBC_2.9 GLIBC_2.10 GLIBC_2.11 GLIBC_2.12 GLIBC_2.13 GLIBC_2…...

日产将使用东风纯电平台?官方回应:不是日产品牌
据财联社报道,日产中国在对于“日产将使用东风纯电平台”的传闻进行回应时指出,文中提及的平台将会用于日产在华合资企业的自主品牌,而不是日产品牌本身。这一消息进一步确认了之前每经网的报道,称日产将采用东风汽车最新发布的“…...
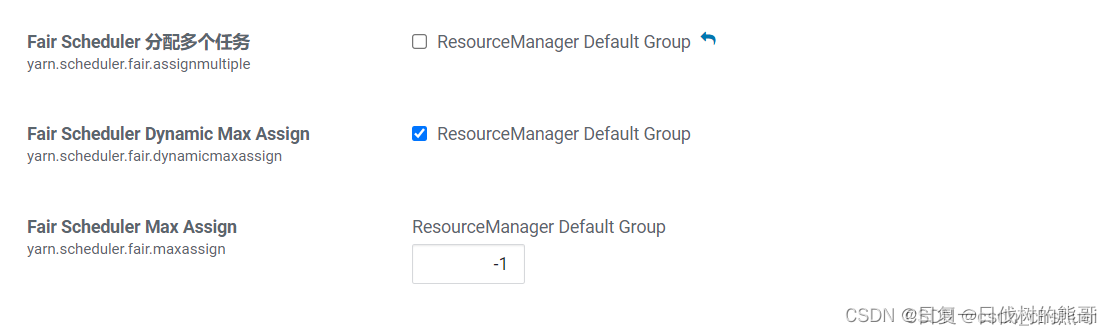
cdh6.3.2 Flink On Yarn taskmanager任务分配倾斜问题的解决办法
业务场景: Flink On Yarn任务启动 组件版本: CDH:6.3.2 Flink:1.13.2 Hadoop:3.0.0 问题描述: 在使用FLink on Yarn调度过程中,发现taskmanager总是分配在集中的几个节点上,集群…...
改进YOLO系列:3.添加SOCA注意力机制
添加SOCA注意力机制 1. SOCA注意力机制论文2. SOCA注意力机制原理3. SOCA注意力机制的配置3.1common.py配置3.2yolo.py配置3.3yaml文件配置1. SOCA注意力机制论文 暂未找到 2. SOCA注意力机制原理 3. SOCA注意力机制的配置 3.1common.py配置 ./models/common.p…...

SpringBoot整合Mybatis Plus——条件构造器Wrapper
Mybatis Plus为我们提供了如下的一些条件构造器,我们可以利用它们实现查询条件、删除条件、更新条件的构造。 条件构造器 | MyBatis-Plus (baomidou.com) 一、通过maven坐标引入依赖(注意版本!!) <dependency>…...

while循环语句
# while循环 # 通过while循环,计算1到100的总和 num 1 sum 0 while num < 100:sum num sumnum 1 print(f"1到100的和为{sum}") #嵌套语句--实现猜1-10数字游戏 import random flagTrue numrandom.randint(1,10) while flag:guess_numint(input(&q…...
)详细介绍】)
【ARM 嵌入式 编译系列 11 -- GCC __attribute__((packed))详细介绍】
文章目录 __attribute__((packed)) 介绍上篇文章:ARM 嵌入式 编译系列 10.3 – GNU elfutils 工具小结 下篇文章:ARM 嵌入式 编译系列 11.1 – GCC attribute((aligned(x)))详细介绍 attribute((packed)) 介绍 __attribute__((packed)) 是 GCC 编译器的一个特性,它可以…...

Pytorch-day06-复杂模型构建-checkpoint
1、PyTorch 复杂模型构建 1、模型截图2、模型部件实现3、模型组装 2、模型定义 2.1、Sequential 1、当模型的前向计算为简单串联各个层的计算时, Sequential 类可以通过更加简单的方式定义模型。2、可以接收一个子模块的有序字典(OrderedDict) 或者一系列子模块…...

windows电脑系统自带的画图工具如何实现自由拼图
1.首先选中你要拼接的第一张图片,右键选着编辑,会自动打开自带的画图工具 然后就是打开第一张图片,如下图所示 接着就是将画布托大,如下图所示。 然后点击选择,选择下面的空白区域,选着区域的范围要比准备拼…...

直线模组的运行注意事项
直线模组是属于高精密的传动元件,大家都知道,安装不当,直线模组就无法显示其高精度的优势,不仅如此,使用不当也会磨损直线模,针对直线模组的使用安全性事宜,我们切记严苛遵照有关的安全操作规程…...
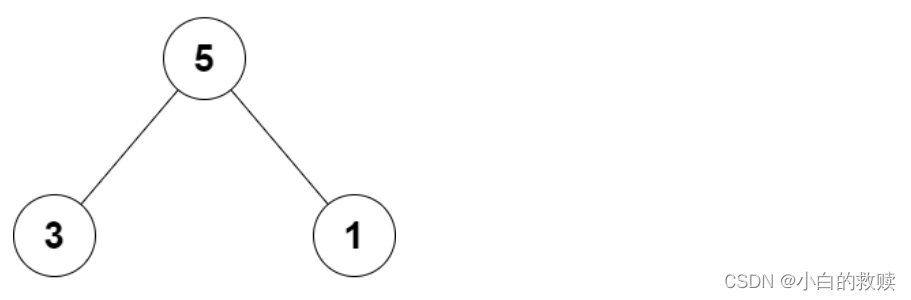
记录每日LeetCode 2236. 判断根结点是否等于子结点之和 Java实现
题目描述: 给你一个 二叉树 的根结点 root,该二叉树由恰好 3 个结点组成:根结点、左子结点和右子结点。 如果根结点值等于两个子结点值之和,返回 true ,否则返回 false 。 初始代码: /*** Definition f…...

使用PHP生成MySQL数据字典
一个项目完成之后,按照需求,我需要给这个项目写设计文档,数据库字典。 设计文档到时好说,但是数据库字典可真的是有点吓到我了。 项目开始的比较急,最开始建数据库的时候没有用excel写数据库字典。 这几十张表的数据…...
React(7)
1.React Hooks 使用hooks理由 1. 高阶组件为了复用,导致代码层级复杂 2. 生命周期的复杂 3. 写成functional组件,无状态组件 ,因为需要状态,又改成了class,成本高 1.1 useState useState();括号里面处的是初始值;返回的是一个…...

MySQL8.0新特性之用户管理
密码插件,在8.0中替换为了 sha2模式在8.0中不支持grant直接创建用户并授权,必须先建用户后grant授权。 关于密码插件sha2带来的坑? 客户端工具,navicat 、 sqlyog工具不支持(无法连接)主从复制,MGR &…...

强推9个研究生必备的免费论文下载网站
一、文献党下载器 文献党下载器把庞大的中外文献数据库资源集成在一个平台,就是把大量的中外数据库资源整合在一个站(目前文献资源量名列前茅)。不论是中文还是外文文献,不论是哪种文献类型,不论是哪个学科领域该网站…...
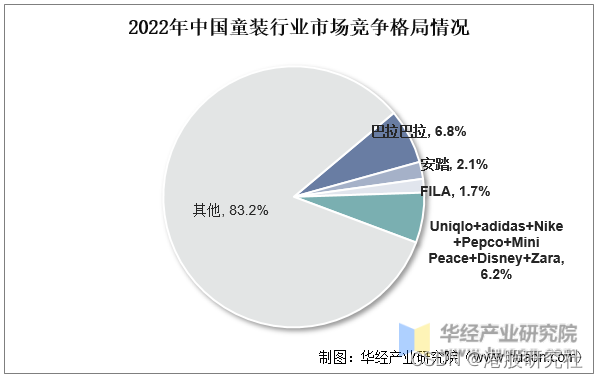
解读2023年上半年财报:继续押注儿童业务的361°,有着怎样的野心?
“足球热”的风还是吹到了青少年身边,近日,济南历城二中女足问鼎2023世界中学生足球锦标赛女子组冠军,中国球队时隔16年再次获得世界中学生足球锦标赛冠军,点燃了不少足球爱好者的热情。 少儿体育热之下,与之相关的运…...

音视频 ffplay播放控制
选项说明q, ESC退出播放f全屏切换p, SPC暂停m静音切换9, 09减少音量,0增加音量a循环切换音频流v循环切换视频流t循环切换字幕流c循环切换节目w循环切换过滤器或显示模式s逐帧播放left/right向后/向前拖动10秒down/up向后/向前拖动1分钟鼠标右键单击拖动与显示宽度对…...
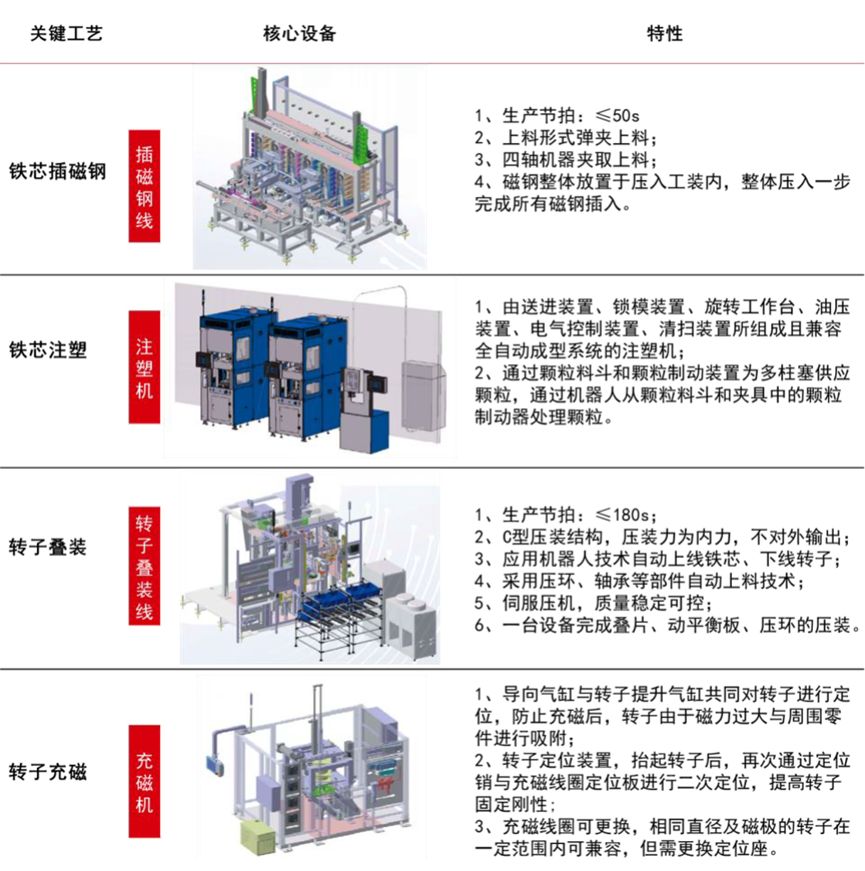
扁线电机定子转子工艺及自动化装备
售:扁线电机 电驱对标样件 需要请联:shbinzer (拆车邦) 新能源车电机路线大趋势,自动化装配产线需求迫切永磁同步电机是新能源车驱动电机的主要技术路线。目前新能源车上最广泛应用的类型为永磁同步电机,…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...
