算法刷题打卡第95天: 最大平均通过率
最大平均通过率
难度:中等
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] = [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学生可以通过考试。
给你一个整数 extraStudents ,表示额外有 extraStudents 个聪明的学生,他们 一定 能通过任何班级的期末考。你需要给这 extraStudents 个学生每人都安排一个班级,使得 所有 班级的 平均 通过率 最大 。
一个班级的 通过率 等于这个班级通过考试的学生人数除以这个班级的总人数。平均通过率 是所有班级的通过率之和除以班级数目。
请你返回在安排这 extraStudents 个学生去对应班级后的 最大 平均通过率。与标准答案误差范围在 10−510^{-5}10−5 以内的结果都会视为正确结果。
示例 1:
输入:classes = [[1,2],[3,5],[2,2]], extraStudents = 2
输出:0.78333
解释:你可以将额外的两个学生都安排到第一个班级,平均通过率为 (3/4 + 3/5 + 2/2) / 3 = 0.78333 。
示例 2:
输入:classes = [[2,4],[3,9],[4,5],[2,10]], extraStudents = 4
输出:0.53485
优先队列
思路:
由于班级总数不会变化,因此题目所求「最大化平均通过率」等价于「最大化总通过率」。设某个班级的人数为 total\textit{total}total,其中通过考试的人数为 pass\textit{pass}pass,那么给这个班级安排一个额外通过考试的学生,其通过率会增加:
pass+1total+1−passtotal\frac{\textit{pass} + 1}{\textit{total} + 1} - \frac{\textit{pass}}{\textit{total}}total+1pass+1−totalpass
我们会优先选择通过率增加量最大的班级,这样做的正确性在于给同一个班级不断地增加安排的学生数量时,其增加的通过率是单调递减的,即:
pass+2total+2−pass+1total+1<pass+1total+1−passtotal\frac{\textit{pass} + 2}{\textit{total} + 2} - \frac{\textit{pass} + 1}{\textit{total} + 1} < \frac{\textit{pass} + 1}{\textit{total} + 1} - \frac{\textit{pass}}{\textit{total}}total+2pass+2−total+1pass+1<total+1pass+1−totalpass
因此当以下条件满足时,班级 jjj 比班级 iii 优先级更大:
passi+1totali+1−passitotali<passj+1totalj+1−passjtotalj\frac{\textit{pass}_i + 1}{\textit{total}_i + 1} - \frac{\textit{pass}_i}{\textit{total}_i} < \frac{\textit{pass}_j + 1}{\textit{total}_j + 1} - \frac{\textit{pass}_j}{\textit{total}_j}totali+1passi+1−totalipassi<totalj+1passj+1−totaljpassj
化简后可得:
(totalj+1)×(totalj)×(totali−passi)<(totali+1)×(totali)×(totalj−passj)(\textit{total}_j + 1) \times (\textit{total}_j) \times (\textit{total}_i - \textit{pass}_i) < (\textit{total}_i + 1) \times (\textit{total}_i) \times (\textit{total}_j - \textit{pass}_j)(totalj+1)×(totalj)×(totali−passi)<(totali+1)×(totali)×(totalj−passj)我们按照上述比较规则将每个班级放入优先队列中,进行 extraStudents\textit{extraStudents}extraStudents次操作。每一次操作,我们取出优先队列的堆顶元素,令其 pass\textit{pass}pass和 total\textit{total}total分别加 111,然后再放回优先队列。
最后我们遍历优先队列的每一个班级,计算其平均通过率即可得到答案。
复杂度分析:
- 时间复杂度: O((n+m)logn)O((n + m)\log n)O((n+m)logn) 或 O(n+mlogn)O(n + m\log n)O(n+mlogn),其中 nnn 为 classes\textit{classes}classes的长度,mmm 等于 extraStudents\textit{extraStudents}extraStudents。每次从优先队列中取出或者放入元素的时间复杂度为 O(logn)O(\log n)O(logn),共需操作 O(n+m)O(n + m)O(n+m) 次,故总复杂度为 O((n+m)logn)O((n + m)\log n)O((n+m)logn)。堆化写法的时间复杂度为 O(n+mlogn)O(n + m\log n)O(n+mlogn)。
- 空间复杂度: O(n)O(n)O(n) 或 O(1)O(1)O(1)。使用优先队列需要用到 O(n)O(n)O(n) 的空间,但若直接在 classes\textit{classes}classes上原地堆化,则可以做到 O(1)O(1)O(1) 额外空间。
import heapq
class Solution:def maxAverageRatio(self, classes: List[List[int]], extraStudents: int) -> float:def increasing_rate(a, b):return (a+1)/(b+1)-a/blis = []for i in classes:heapq.heappush(lis, (-increasing_rate(i[0], i[1]), i))for i in range(extraStudents):now = heapq.heappop(lis)[1]heapq.heappush(lis, (-increasing_rate(now[0]+1, now[1]+1), [now[0]+1, now[1]+1]))return sum([i[1][0]/i[1][1] for i in lis]) / len(lis)
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/maximum-average-pass-ratio
相关文章:

算法刷题打卡第95天: 最大平均通过率
最大平均通过率 难度:中等 一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali…...
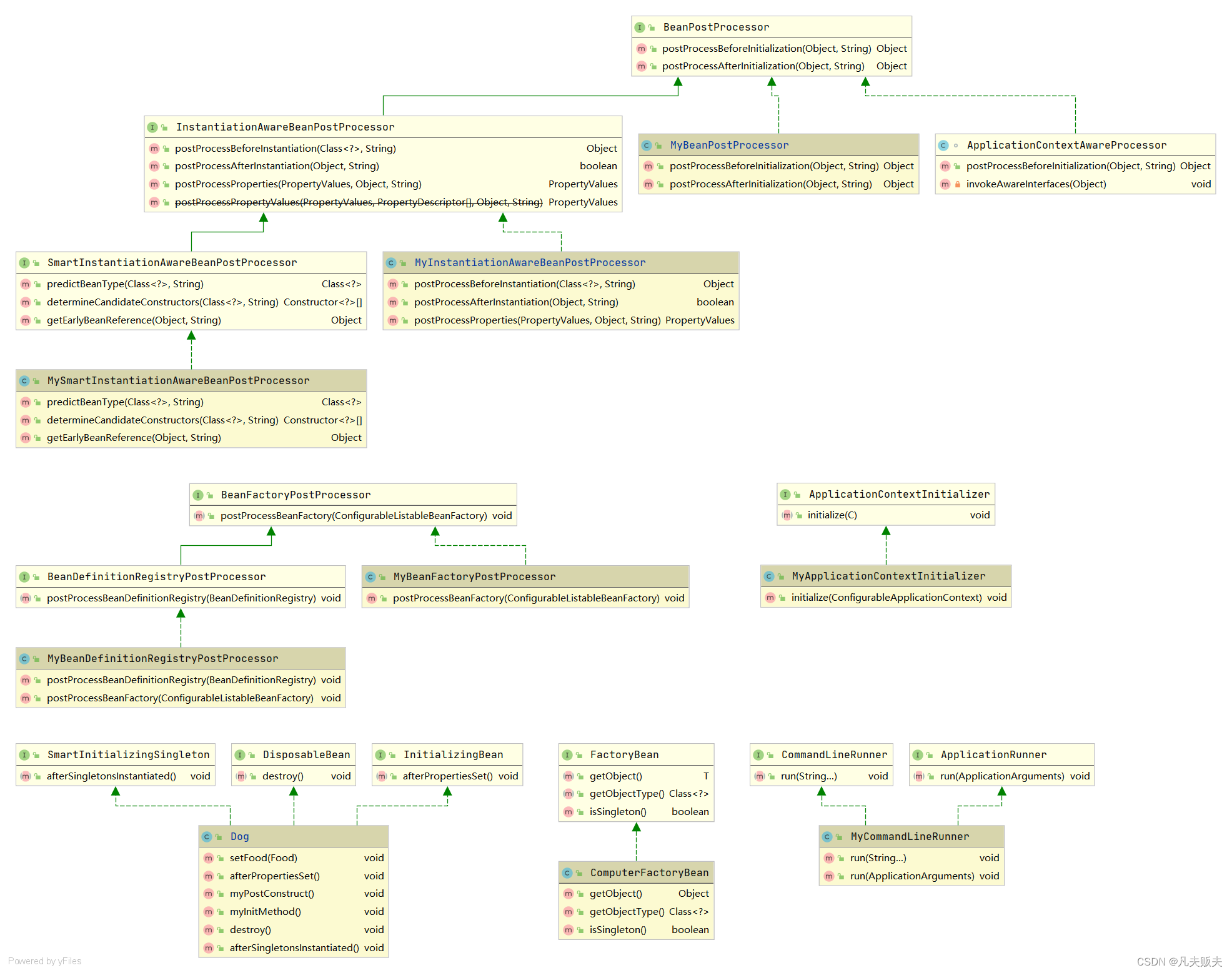
Springboot扩展点系列之终结篇:Bean的生命周期
前言关于Springboot扩展点系列已经输出了13篇文章,分别梳理出了各个扩展点的功能特性、实现方式和工作原理,为什么要花这么多时间来梳理这些内容?根本原因就是这篇文章:Spring bean的生命周期。你了解Spring bean生命周期…...
OnGUI Color 控件||Unity 3D GUI 简介||OnGUI TextField 控件
Unity 3D Color 控件与 Background Color 控件类似,都是渲染 GUI 颜色的,但是两者不同的是 Color 不但会渲染 GUI 的背景颜色,同时还会影响 GUI.Text 的颜色。具体使用时,要作如下定义:public static var color:Color;…...

【日刻一诗】
日刻一诗 1)LeetCode总结(线性表)_链表类 2)LeetCode总结(线性表)_栈队列类 3)LeetCode总结(线性表)_滑动窗口 4)LeetCode总结(线性表&#x…...
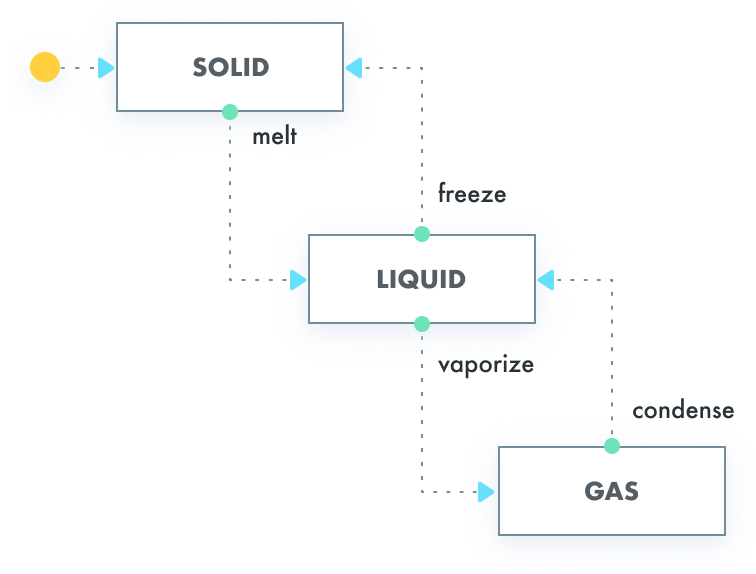
设计模式 状态机
前言 本文梳理状态机概念,在实操中状态机和状态模式类似,只是被封装起来,可以很方便的实现状态初始化和状态转换。 概念 有限状态机(finite-state machine)又称有限状态自动机(英语:finite-s…...

React源码分析(二)渲染机制
准备工作 为了方便讲解,假设我们有下面这样一段代码: function App(){const [count, setCount] useState(0)useEffect(() > {setCount(1)}, [])const handleClick () > setCount(count > count)return (<div>勇敢牛牛, <sp…...

Object.defineProperty 和 Proxy 的区别
区别:Object.defineProperty是一个用来定义对象的属性或者修改对象现有的属性的函数,,而 Proxy 是一个用来包装普通对象的对象的对象。Object.defineProperty是vue2响应式的原理, Proxy 是vue3响应式的原理1)参数不同Object.defineProperty参数obj: 要定…...

Python基础4——面向对象
目录 1. 认识对象 2. 成员方法 2.1 成员方法的定义语法 3. 构造方法 4. 其他的一些内置方法 4.1 __str__字符串方法 4.2 __lt__小于符号比较方法 4.3 __le__小于等于符号比较方法 4.4 __eq__等号比较方法 5. 封装特性 6. 继承特性 6.1 单继承 6.2 多继承 6.3 pas…...

Hive 核心知识点灵魂 16 问
本文目录 No1. 请谈一下 Hive 的特点No2. Hive 底层与数据库交互原理?No3. Hive 的 HSQL 转换为 MapReduce 的过程?No4. Hive 的两张表关联,使用 MapReduce 怎么实现?No5. 请说明 hive 中 Sort By,Order By࿰…...

聊聊探索式测试与敏捷实践
这是鼎叔的第五十二篇原创文章。行业大牛和刚毕业的小白,都可以进来聊聊。欢迎关注本专栏和微信公众号《敏捷测试转型》,大量原创思考文章陆续推出。探索式测试在敏捷测试象限中处于右上角,即面向业务且评价产品,这篇补充一下探索…...

社区宠物诊所管理系统
目录第一章概述 PAGEREF _Toc4474 \h 21.1引言 PAGEREF _Toc29664 \h 31.2开发背景 PAGEREF _Toc3873 \h 3第二章系统总体结构及开发 PAGEREF _Toc19895 \h 32.1系统的总体设计 PAGEREF _Toc6615 \h 32.2开发运行环境 PAGEREF _Toc13054 \h 3第三章数据库设计 PAGEREF _Toc2852…...

Vue项目创建首页发送axios请求
这是个全新的Vue项目,引入了ElementUI 将App.vue里的内容干掉,剩如下 然后下面的三个文件也可以删掉了 在views文件下新建Login.vue组件 到router目录下的index.js 那么现在的流程大概是这样子的 启动 写登陆页面 <template><div><el-form :ref"form"…...

Nginx
NginxNginxNginx可以从事的用途Nginx安装Nginx自带常用命令Nginx启动Nginx停止Nginx重启Nginx配置概要第一部分:全局块第二部分:events 块:第三部分:http块:Nginx Nginx是一个高性能的http和反向代理服务器࿰…...
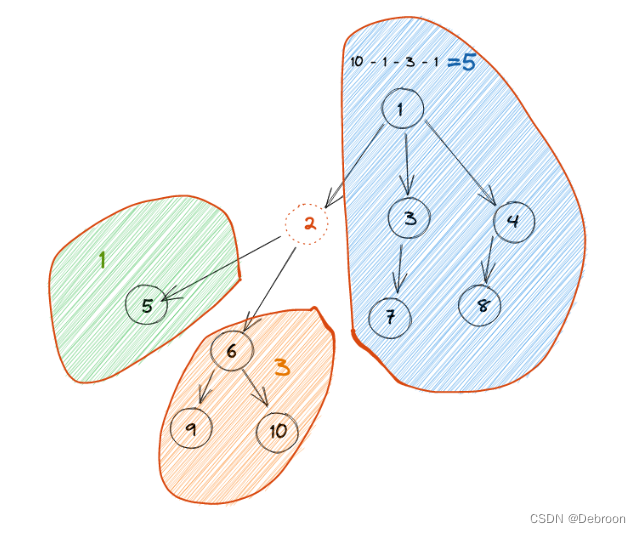
2049. 统计最高分的节点数目
2049. 统计最高分的节点数目题目算法设计:深度优先搜索题目 传送门:https://leetcode.cn/problems/count-nodes-with-the-highest-score/ 算法设计:深度优先搜索 这题的核心是计算分数。 一个节点的分数 左子树节点数 右子树节点数 除自…...

Docker 架构简介
Docker 架构 Docker 包括三个基本概念: 镜像(Image):Docker 镜像(Image),就相当于是一个 root 文件系统。比如官方镜像 ubuntu:16.04 就包含了完整的一套 Ubuntu16.04 最小系统的 root 文件系统。容器&am…...
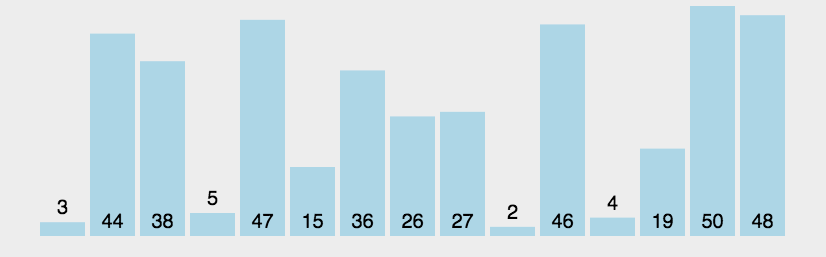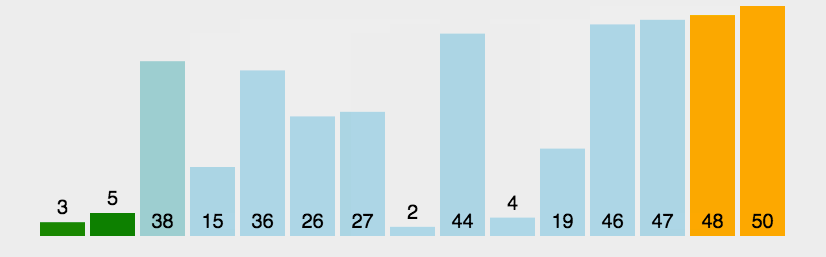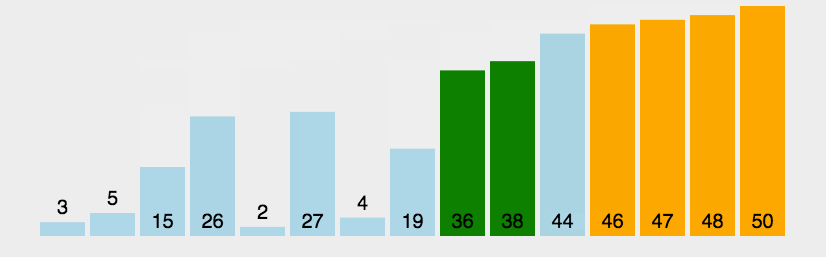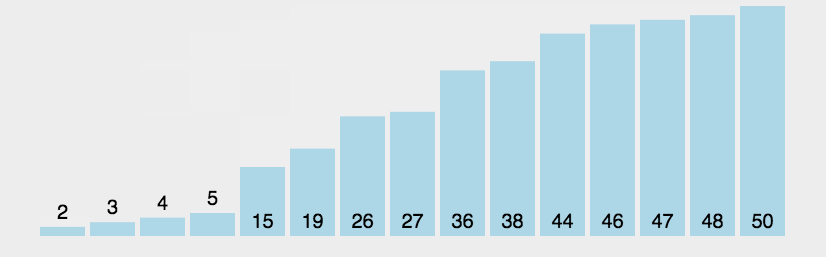
玄子Share-BCSP助学手册-JAVA开发
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-b2gPyAnt-1676810001349)(./assets/%E7%8E%84%E5%AD%90Share%E4%B8%89%E7%89%88.jpg)] 玄子Share-BCSP助学手册-JAVA开发 前言: 此文为玄子,复习BCSP一二期后整理的文章&#x…...

利用React实现多个场景下的鼠标跟随框提示框
前言 鼠标跟随框的作用如下图所示,可以在前端页面上,为我们后续的鼠标操作进行提示说明,提升用户的体验。本文将通过多种方式去实现,从而满足不同场景下的需求。 实现原理 实现鼠标跟随框的原理很简单,就是监听鼠标在…...
【安全知识】——如何绕过cdn获取真实ip
作者名:白昼安全主页面链接: 主页传送门创作初心: 以后赚大钱座右铭: 不要让时代的悲哀成为你的悲哀专研方向: web安全,后渗透技术每日鸡汤: 现在的样子是你想要的吗?cdn简单来说就是…...
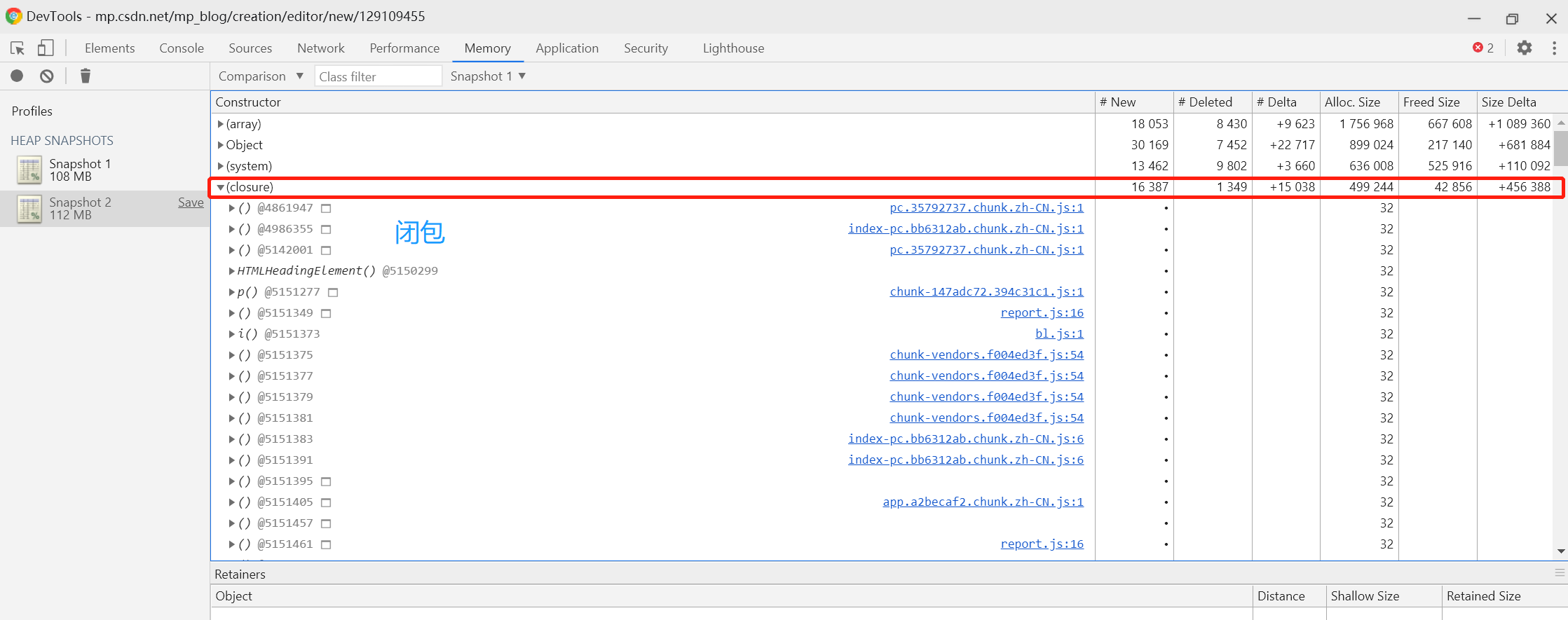
JavaScript内存泄露和垃圾回收机制
1、是什么?内存泄露(Memory leak)是在计算机科学中,由于疏忽或错误造成程序未能释放已经不再使用的内存。并非指内存在物理上的消失,而是应用程序分配某段内存后,由于设计错误,导致在释放该段内…...

Kubernetes02:知识图谱
Kubernetes01:知识图谱 MESOS APACHE 分布式资源管理框架 2019-5 Twitter 》 Kubernetes Docker Swarm 2019-07 阿里云宣布 Docker Swarm 剔除 Kubernetes Google 10年容器化基础架构 borg Go语言 Borg 特点 轻量级:消耗资源小 开源 弹性伸缩 负载均…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
