法线矩阵推导
法线矩阵推导
https://zhuanlan.zhihu.com/p/72734738
https://juejin.cn/post/7113952418613690382
https://blog.csdn.net/wangjianxin97?type=blog
1、为什么需要法线矩阵
vec3 normalEyeSpace = modelViewMatrix * normal;
如果模型矩阵执行了非等比缩放, 顶点的改变会导致法向量不再保持垂直关系。
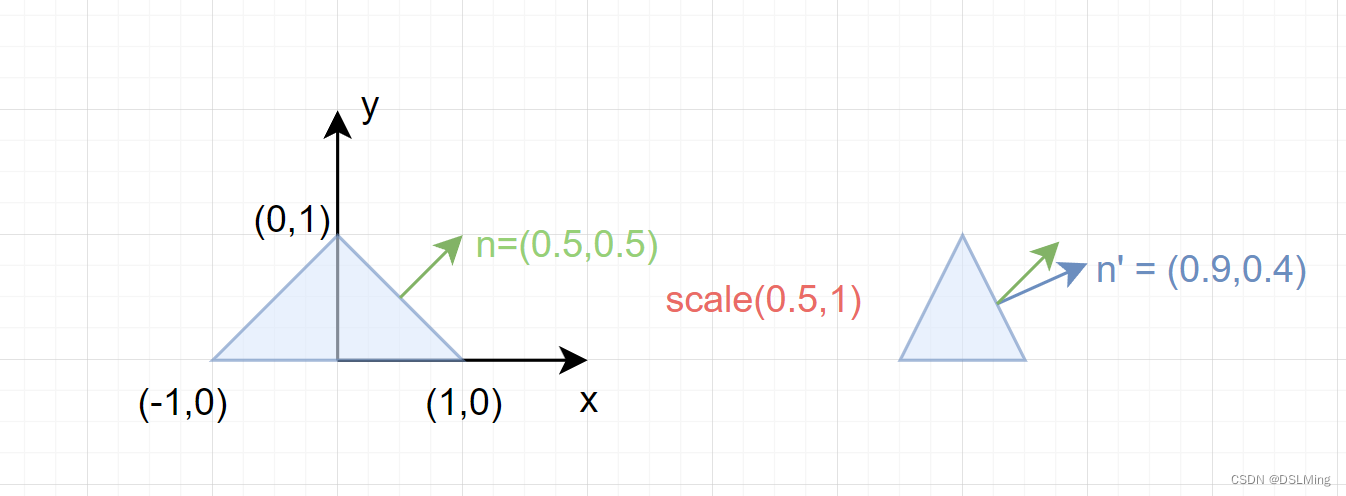
缩放后 n n n不在与线段垂直了, 真正垂直的是 n ′ n' n′。
three.js 代码:
const geometry = new THREE.BufferGeometry()
const position = [];
const normals = [];
position.push(-1, 0, 0)
position.push(1, 0, 0)
position.push(0, 1, 0)normals.push(0.5, 0.5, 0)
normals.push(0.5, 0.5, 0)
normals.push(0.5, 0.5, 0)geometry.setAttribute('position', new THREE.Float32BufferAttribute(position, 3))
geometry.setAttribute('normal', new THREE.Float32BufferAttribute(normals, 3))const material = new THREE.ShaderMaterial({vertexShader: `varying vec3 vNormal;void main() {vec4 mvPosition = modelViewMatrix * vec4( position, 1.0 );gl_Position = projectionMatrix * mvPosition;vNormal = normal;}`,fragmentShader: `varying vec3 vNormal;uniform mat3 normalMatrix;void main() {gl_FragColor = vec4( vNormal, 1.0 );}`,
});const mesh = new THREE.Mesh(geometry, material);
mesh.scale.set(0.5, 1, 1)
2 法向量矩阵推导
约定:
- 向量用小写字母的表示
- 转换矩阵用大写字母表示
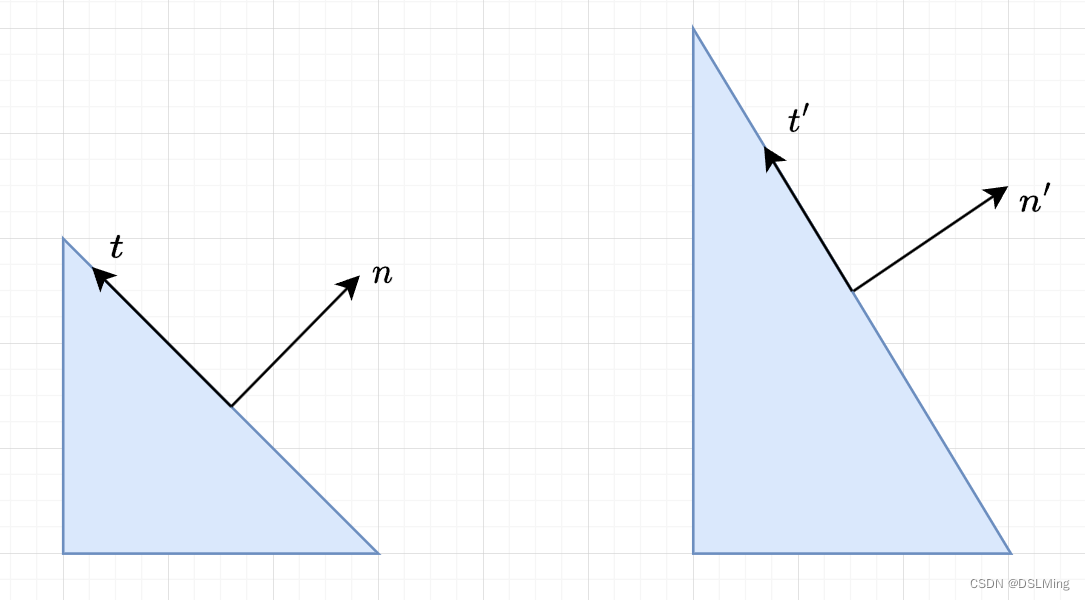
假设矩阵 G G G 转换法向量, 矩阵 M M M转换切线。
如果转换到视图空间,那么 M M M就是modelViewMatrix, 如果转换到世界空间, M M M就是modelMatrix。
根据假设有:
n ′ = G n t ′ = M t n' = G n \\ t' = M t \\ n′=Gnt′=Mt
根据几何关系有:
n ⋅ t = n ′ ⋅ t ′ = 0 n \cdot t = n' \cdot t' = 0 n⋅t=n′⋅t′=0
带入有:
n ′ ⋅ t ′ = ( G n ) ⋅ ( M t ) = ( G n ) T ( M t ) = n T G T M t \begin{aligned} n' \cdot t' &= (G n) \cdot (M t) \\ &= (G n)^{T} (M t) \\ &= n^{T} G^{T} M t \\ \end{aligned} n′⋅t′=(Gn)⋅(Mt)=(Gn)T(Mt)=nTGTMt
因为(向量点积用矩阵表示):
n ⋅ t = n T t = n ′ ⋅ t ′ n \cdot t = n^{T} t = n' \cdot t' n⋅t=nTt=n′⋅t′
所以,满足上式, 只需:
G T M = I G^{T} M = I GTM=I
因此:
G T = M − 1 ( G T ) T = ( M − 1 ) T G = ( M − 1 ) T \begin{aligned} G^{T} &= M^{-1} \\ (G^{T})^{T} &= (M^{-1})^{T} \\ G &= (M^{-1})^{T} \end{aligned} GT(GT)TG=M−1=(M−1)T=(M−1)T
相关文章:

法线矩阵推导
法线矩阵推导 https://zhuanlan.zhihu.com/p/72734738 https://juejin.cn/post/7113952418613690382 https://blog.csdn.net/wangjianxin97?typeblog 1、为什么需要法线矩阵 vec3 normalEyeSpace modelViewMatrix * normal;如果模型矩阵执行了非等比缩放, 顶点的改变会导致法…...
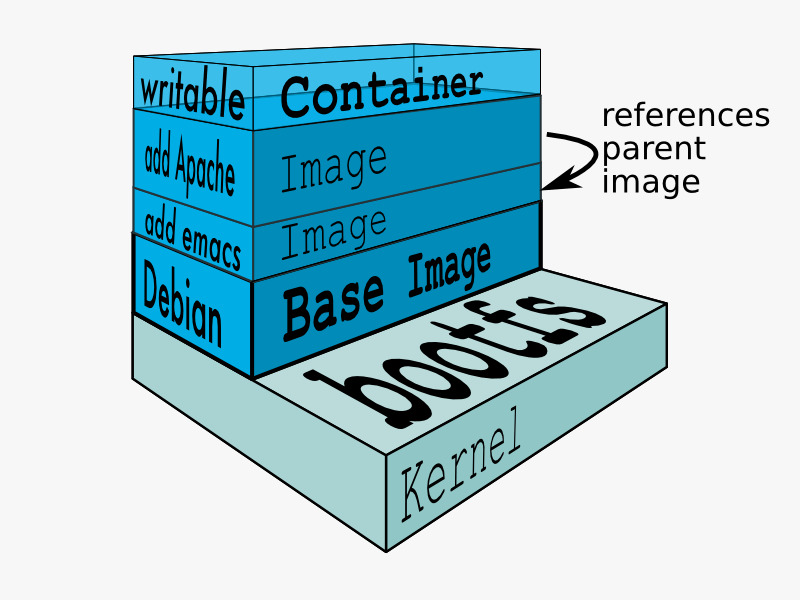
对容器、虚拟机和 Docker 的初学者友好介绍
一、说明 如果你是一个程序员或技术人员,你可能至少听说过Docker:一个有用的工具,用于在“容器”中打包,运输和运行应用程序。很难不这样做,这些天它得到了所有的关注 - 来自开发人员和系统管理员。即使是像谷歌、VMwa…...

linux部署clickhouse(单机)
一、下载安装 1.1、下载地址 阿里巴巴开源镜像站-OPSX镜像站-阿里云开发者社区阿里巴巴开源镜像站,免费提供Linux镜像下载服务,拥有Ubuntu、CentOS、Deepin、MongoDB、Apache、Maven、Composer等多种开源软件镜像源,此外还提供域名解析DNS、…...

vue组件注册
组件注册分为全局注册和局部注册 全局注册 在 main.js 或者入口文件中 import { createApp } from vue; import MyComponent from ./components/MyComponent.vue;const app createApp();app.component(my-component, MyComponent);app.mount(#app); 我们首先通过createApp…...
day20 飞机大战射击游戏
有飞行物类 飞行 爆炸 的连环画, 飞行的背景图 , 子弹图, 还有游戏开始 暂停 结束 的画面图。 设计一个飞机大战的小游戏, 玩家用鼠标操作hero飞行机, 射出子弹杀死敌机,小蜜蜂。 敌机可以获得分数&…...
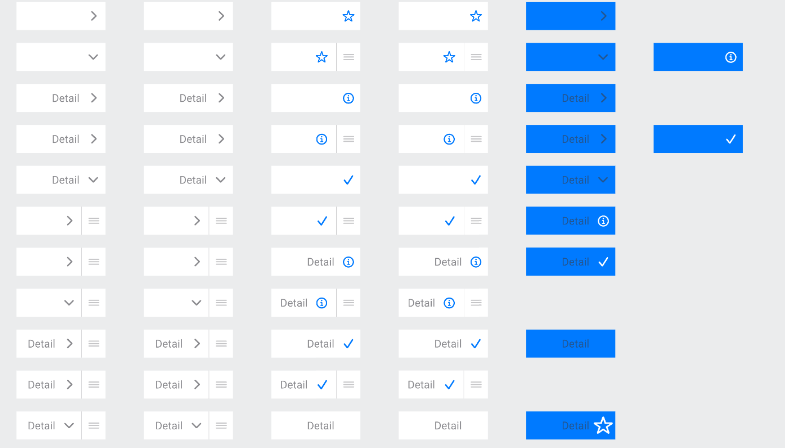
iOS设计规范是什么?都有哪些具体规范
iOS设计规范是苹果为移动设备操作系统iOS制定的设计指南。iOS设计规范的制定保证了苹果应用在外观和操作上的一致性和可用性,从而提高了苹果界面设计的用户体验和应用程序的成功性。本文将从七个方面全面分析iOS设计规范。 1.iOS设计规范完整版分享 由「即时设计」…...

动手学深度学习-pytorch版本(二):线性神经网络
参考引用 动手学深度学习 1. 线性神经网络 神经网络的整个训练过程,包括: 定义简单的神经网络架构、数据处理、指定损失函数和如何训练模型。经典统计学习技术中的线性回归和 softmax 回归可以视为线性神经网络 1.1 线性回归 回归 (regression) 是能为一个或多个…...
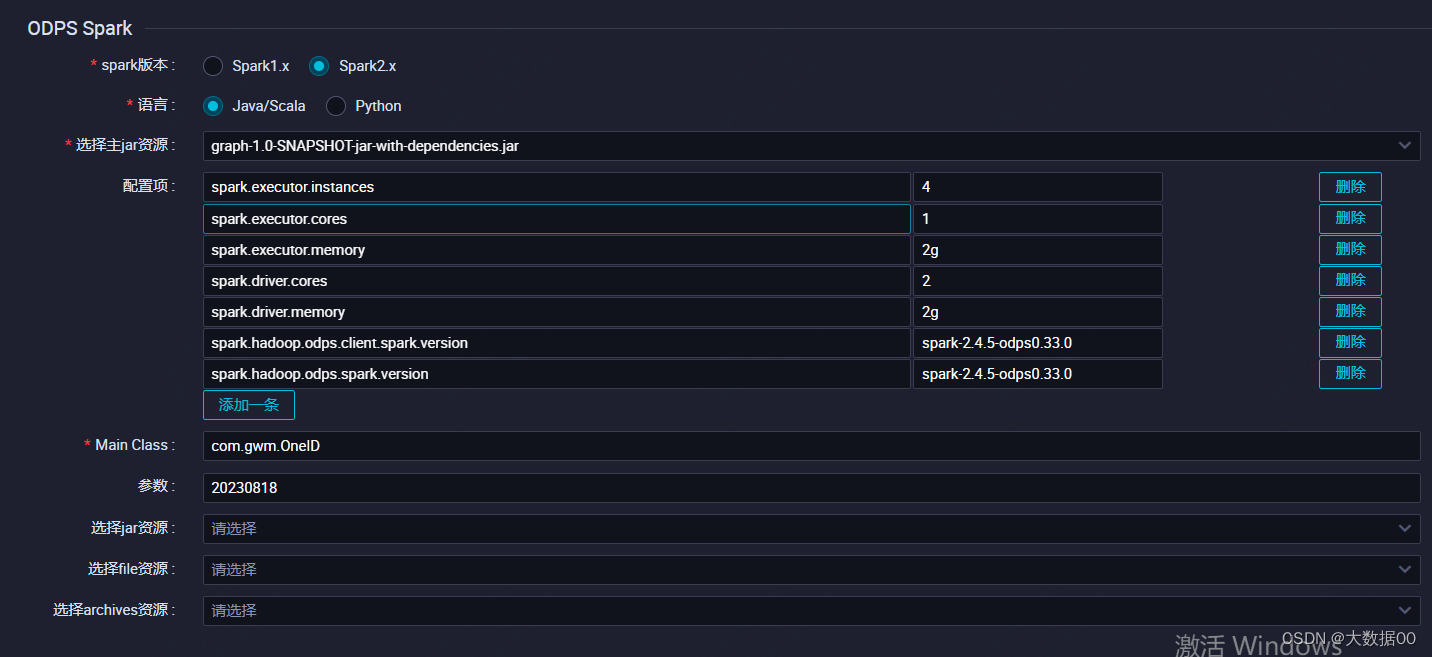
Spark 图计算ONEID 进阶版
0、环境信息 本文采用阿里云maxcompute的spark环境为基础进行的,搭建本地spark环境参考搭建Windows开发环境_云原生大数据计算服务 MaxCompute-阿里云帮助中心 版本spark 2.4.5,maven版本大于3.8.4 ①配置pom依赖 详见2-1 ②添加运行jar包 ③添加配置信…...

Comparable和Comparator区别
Comparable和Comparator接口都是实现集合中元素的比较、排序的,众所周知,诸如Integer,double等基本数据类型,java可以对他们进行比较,而对于类的比较,需要人工定义比较用到的字段比较逻辑。总体来讲&#x…...

JAVA知识点梳理
我的博客:lcatake_flume,spark,zookeeper-CSDN博客 看不懂的话进去看看 1.Java的三个版本 JAVASE 基本 JAVAME 微缩 JAVAEE 标准 3.java的特点 面向对象 跨平台:jvm将java文件转变为字节码文件(.class)在多个系统中运 行字…...
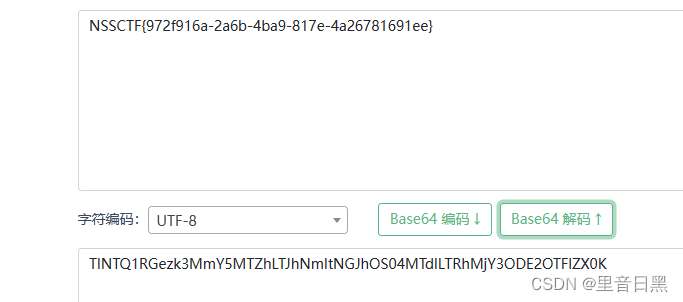
[SWPUCTF 2022 新生赛]ez_ez_php
这段代码是一个简单的PHP文件处理脚本。让我们逐行进行分析: error_reporting(0); - 这行代码设置了错误报告的级别为0,意味着不显示任何错误。 if (isset($_GET[file])) { - 这行代码检查是否存在一个名为"file"的GET参数。 if ( substr($_…...
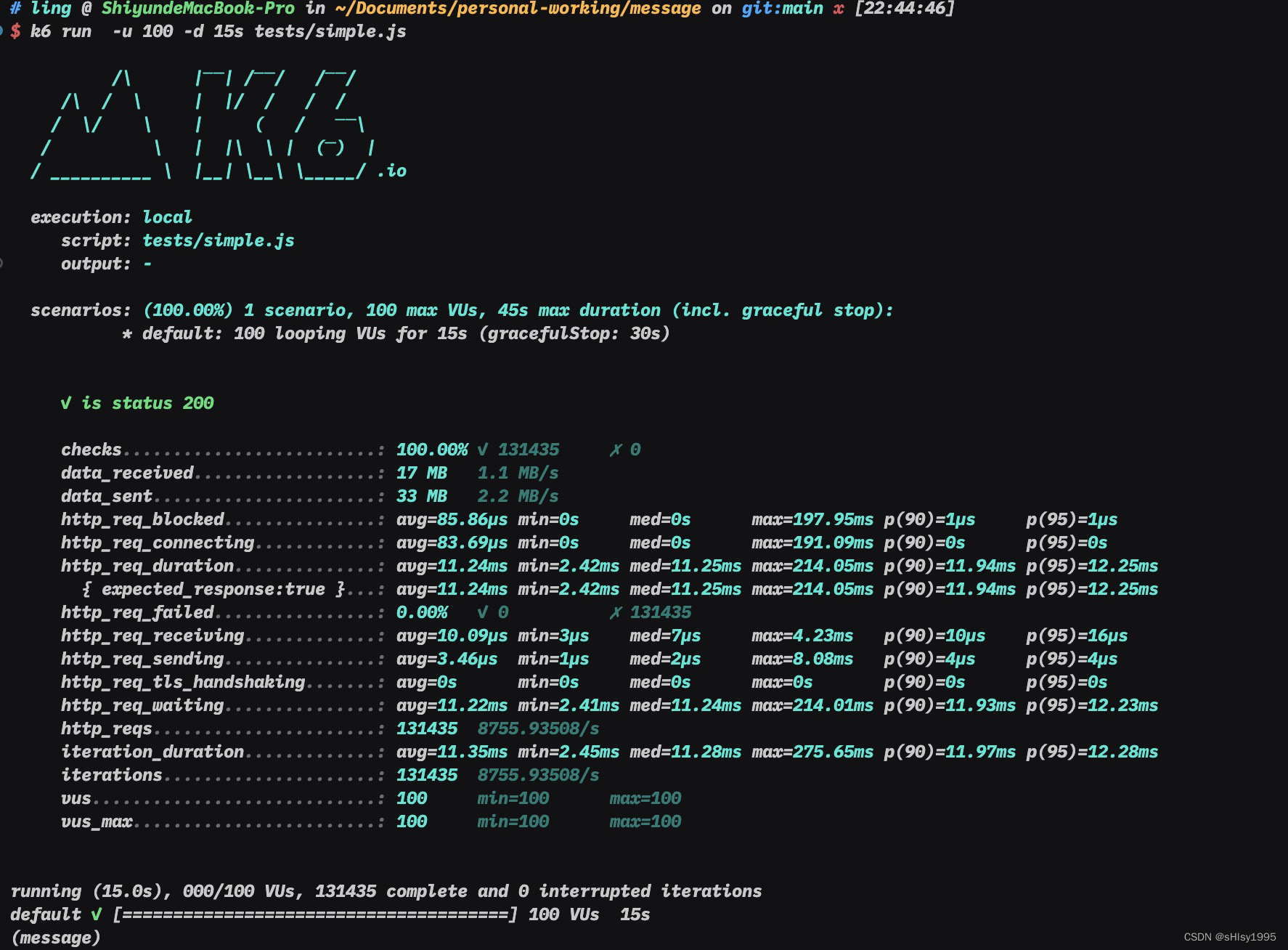
GraphQL strawberry的使用回顾和体会
GraphQL vs RESTful 简单来说GraphQL 比起 RESTful 集成额外一些功能 出入参校验、序列化 (简化后端编程)自由可选的返回数据字段 (简化一些多余接口开发和沟通联调成本) 这些都是优点了。 开发效率在项目初期是很重要的,需要快速原型化。 但是后期稳定后&#…...

08无监督学习——聚类
1.什么是聚类任务? 类别:无监督学习 目的:通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。 1.1K均值聚类 步骤: 随机选取样本作为初始均值向量(初始值:k的值【即几个簇】)分别…...

Python使用OpenCV库对彩色图像进行通道分离
目录 1、解释说明: 2、使用示例: 3、注意事项: 1、解释说明: 在Python中,我们可以使用OpenCV库对彩色图像进行通道分离。通道分离是将彩色图像的每个像素分解为三个通道(红、绿、蓝)的过程。…...

前端面试:【CSS】盒模型、选择器、布局、响应式设计、Flexbox 与 Grid
CSS(层叠样式表)是用于控制网页外观和布局的重要语言。在这篇文章中,我们将深入探讨CSS的基础知识,包括盒模型、选择器、布局、响应式设计,以及弹性盒子(Flexbox)和网格布局(Grid&am…...

深入浅出通过PHP封装根据商品ID获取抖音商品详情数据方法
抖音商城商品详情数据是指商品在抖音商城中的展示信息,包括商品的标题、描述、价格、图片等。商家可以通过商品详情数据了解用户对商品的兴趣和需求,从而进行优化和调整。 商品详情数据还可以帮助商家评估商品的销售情况和市场竞争力,为制定…...
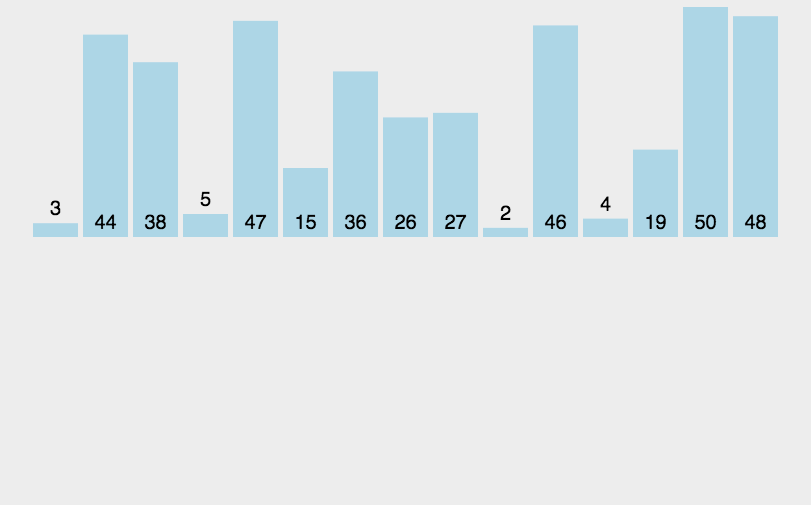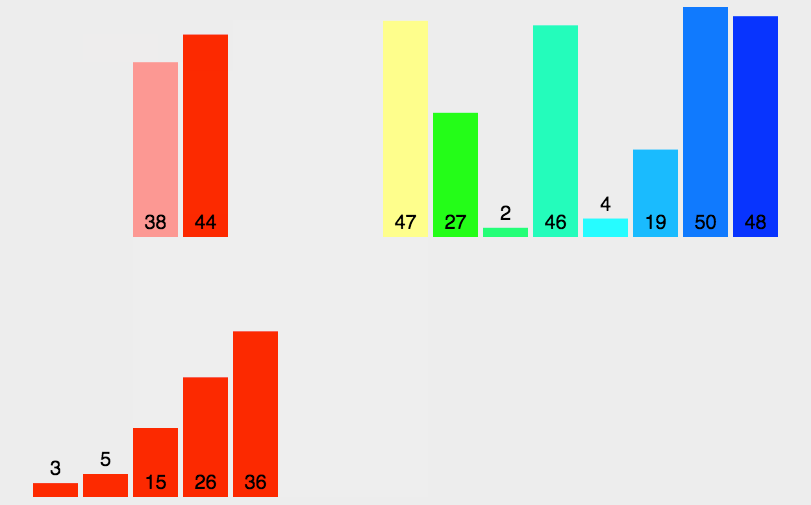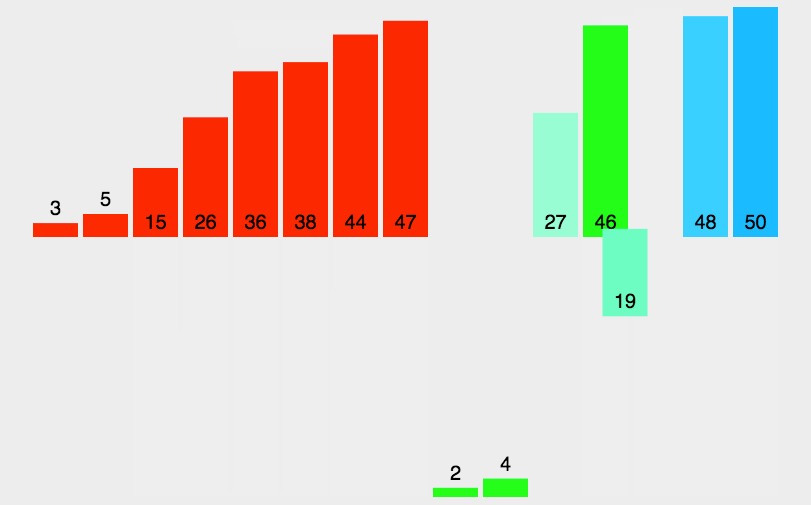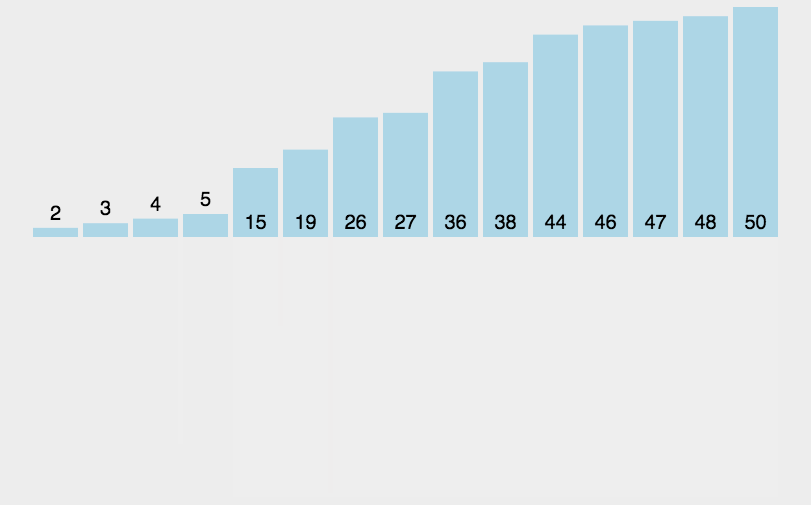
排序(七种排序)
1.插入排序 2.希尔排序 3.选择排序 4.堆排序 5.冒泡排序 6.快速排序 7.归并排序 1.插入排序 1.1思路 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 1.2实现 //插入排…...
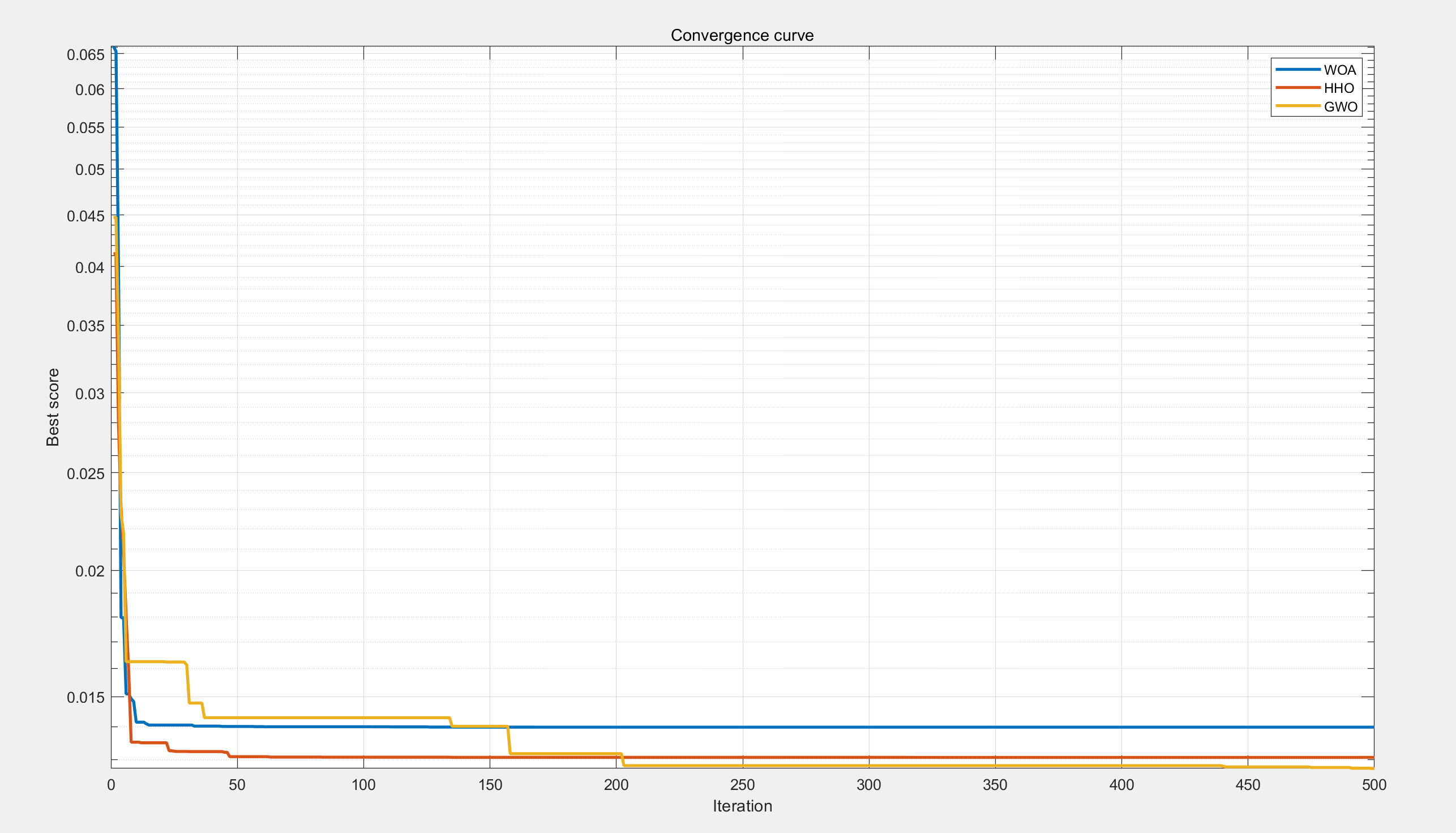
【工程优化问题】基于鲸鱼、萤火虫、灰狼优化算法的张力、压缩弹簧设计问题研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

sap ui5刷新页面的方式
1.第一种 window.location.reload();2.第二种 如果你想在UI5应用程序中使用MVC模式来处理页面刷新,可以通过重新加载当前路由来实现刷新。首先,确保你有一个Router对象实例: var oRouter = sap.ui.core.UIComponent.getRouterFor(this);然后&...

Java课题笔记~ Fastjson 概述
3.3 JSON串和Java对象的相互转换 学习完 json 后,接下来聊聊 json 的作用。 以后我们会以 json 格式的数据进行前后端交互。前端发送请求时,如果是复杂的数据就会以 json 提交给后端;而后端如果需要响应一些复杂的数据时,也需要…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
