当前位置： 首页 > news >正文

excel常见的数学函数篇2

news 2026/2/8 9:21:22

一、数学函数

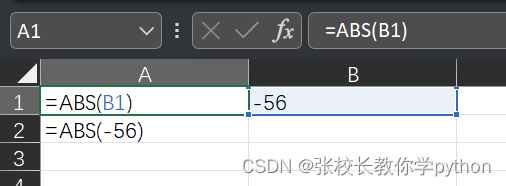
1、ABS(number)：返回数字的绝对值

语法：ABS(数字)；返回数字的绝对值；若引用单元格，把数字换为单元格地址即可

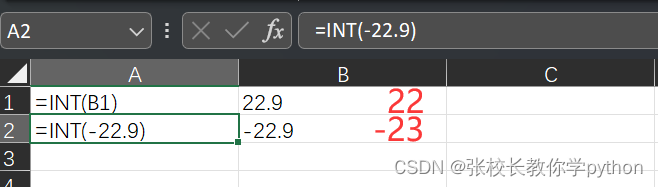
在这里插入图片描述

2、INT(number)：向小取整

语法：INT(数字)；若引用单元格，把数字换为单元格地址即可

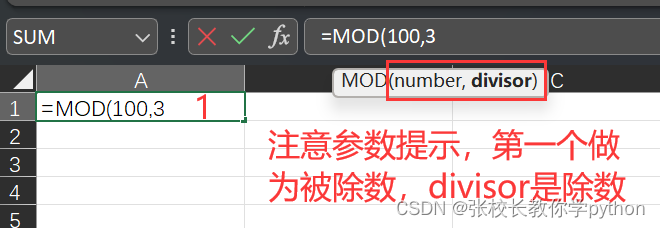
在这里插入图片描述

3、MOD(number,divisor)：返回两数相除的余数（结果的符号和余数相同）

语法：MOD(被除数,除数)；若引用单元格，把数字换为单元格地址即可

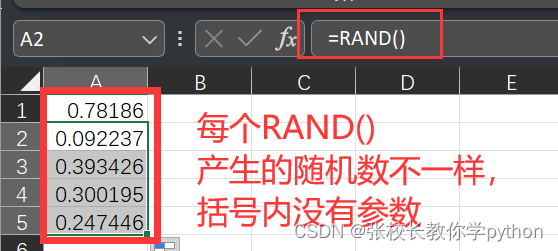
在这里插入图片描述

4、RAND：[0,1)之间的随机数

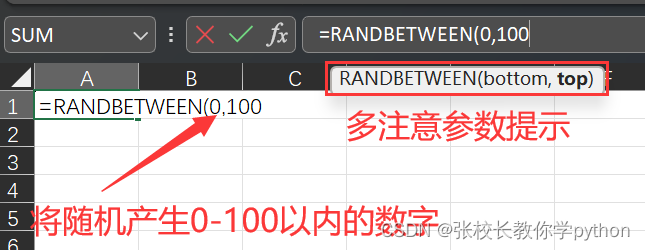
在这里插入图片描述

5、RANDBETWEEN(bottom,top)：[a,b]之间的随机数

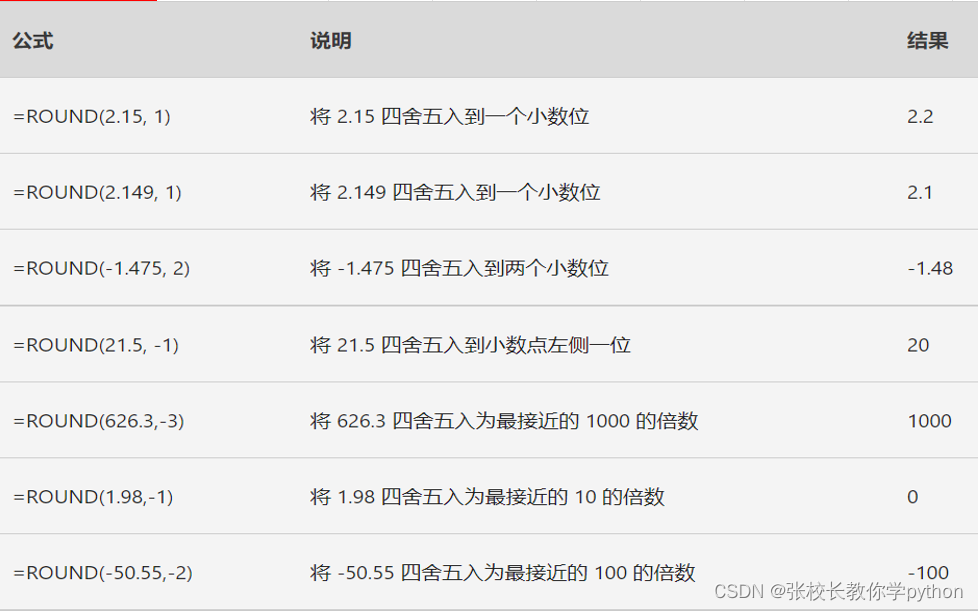
在这里插入图片描述

6、ROUND(number,num_digits)：将数字四舍五入到指定位数

在这里插入图片描述

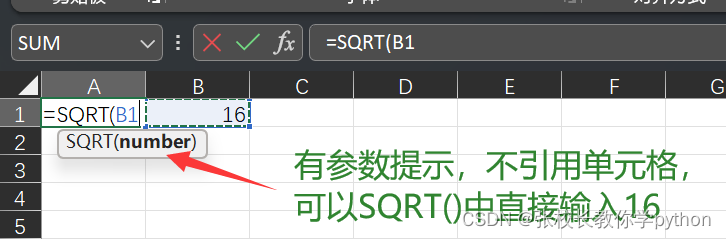
7、SQRT(number)：返回算术平方根

案例：求16的算术平方根

在这里插入图片描述

excel其他数学函数详见：excel中有哪些通配符、excel配置问题，数学函数篇1之sum系列

相关文章：

excel常见的数学函数篇2

一、数学函数 1、ABS(number)：返回数字的绝对值 语法：ABS(数字)；返回数字的绝对值；若引用单元格，把数字换为单元格地址即可 2、INT(number)：向小取整 语法：INT(数字)；若引用单元格…...

编程日记 2023/8/22 2:35:59

Certify The Web (IIS)

一、简介 Certify The Web 适用于 Windows的SSL 证书管理器用户界面，与所有 ACME v2 CA 兼容，为您的 IIS/Windows 服务器轻松地安装和自动更新来自 Letencrypt.org 和其他 ACME 证书授权机构的免费 SSL/TLS 证书，设置 https 从未如此简单。 …...

编程日记 2023/8/22 2:34:55

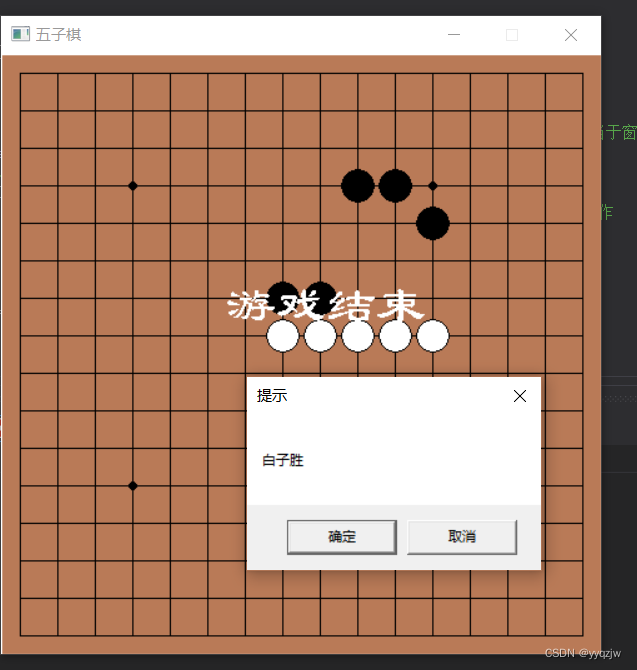
【c语言】五子棋（EasyX图形库+背景音乐）

大家好，有没有觉得写了好多c语言代码，面对的都是黑框框控制台，当我们学习了基础的c语言知识，和EasyX图形库后，终于可以和黑框框saygoodbye,今天要分享给大家的是小游戏五子棋，跟着小张一起学习吧 EasyX图形…...

编程日记 2023/8/22 2:33:54

【OpenCV 】对极几何标定质量验证

标定质量验证&#xff1a; 寻找一对对应点&#xff0c;已经知道对应关系及其详细坐标&#xff0c;根据对极几何推导实现 ///get the camera intrinsics and T_Ci_Bstd::vector<Eigen::Matrix3d> M_K;std::vector<Eigen::Matrix4d> T_Ci_B;for (int i 0; i < ne…...

编程日记 2023/8/22 2:32:52

Netty：ByteBuf的清空操作

说明 io.netty.buffer.ByteBuf有个函数clear()&#xff0c;它可以将ByteBuf的readerIndex和writerIndex都设置为0。 代码示例 package com.thb;import io.netty.buffer.ByteBuf; import io.netty.buffer.Unpooled;public class Demo {public static void main(String[] args…...

编程日记 2023/8/22 2:31:50

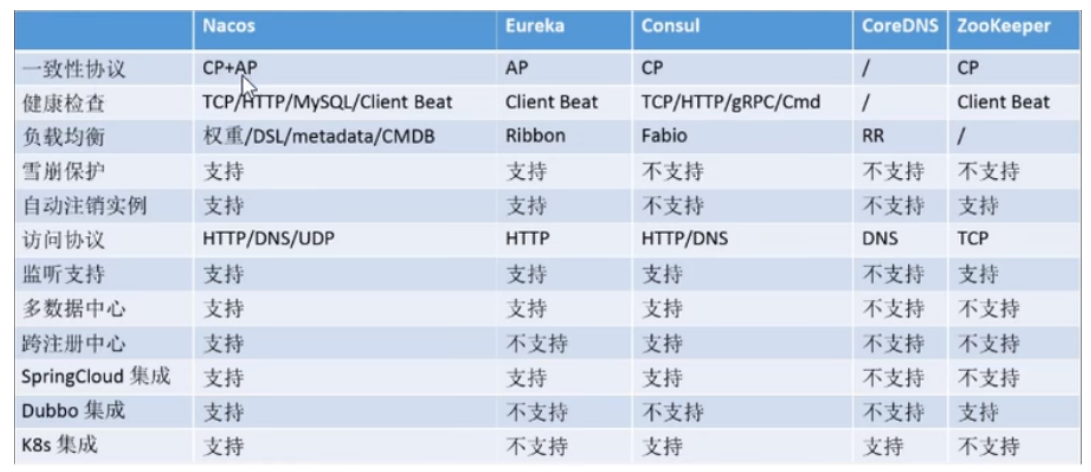
SpringCloud最新最全面试题

目录 一、简单说一说什么是微服务&#xff1f; 二、微服务有哪些优缺点&#xff1f; 三、微服务、分布式、集群的区别&#xff1f; 四、什么是Eureka&#xff1f; 五、Eureka有那两大组件&#xff1f; 六、actuator是什么&#xff1f; 七、Discovery是什么&#xff1f; …...

编程日记 2023/8/22 2:30:46

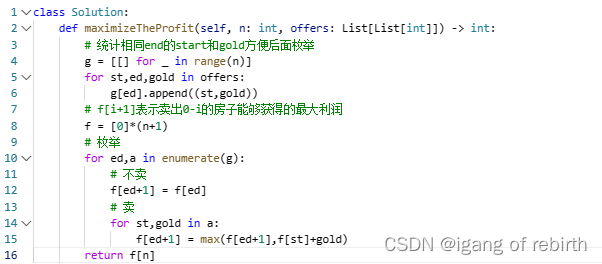
leetcode359周赛

2828. 判别首字母缩略词 核心思想:枚举。只需要枚举首字母和s是否一一对应即可。 2829. k-avoiding 数组的最小总和 核心思想&#xff1a;自己的方法就是哈希表&#xff0c;枚举i的时候&#xff0c;将k-i统计起来&#xff0c;如果出现了那么就跳过。灵神的方法是数学法&#…...

编程日记 2023/8/22 2:29:43

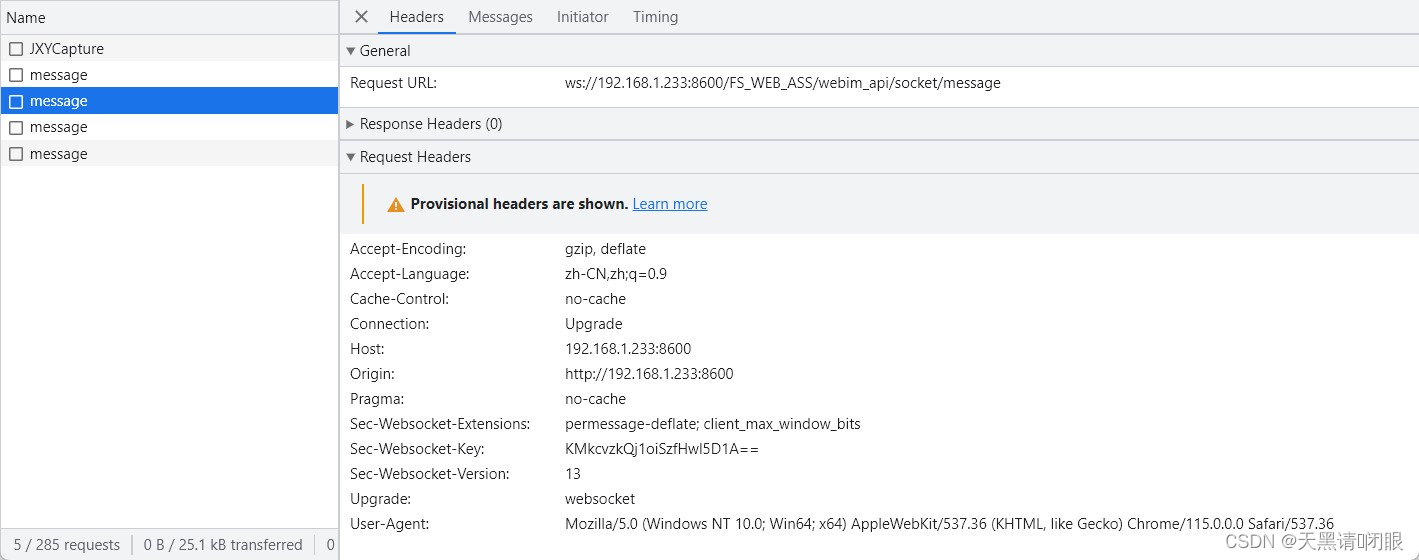
nginx代理webSocket链接响应403

一、场景 使用nginx代理webSocket链接&#xff0c;nginx响应403 1、nginx访问日志响应403 [18/Aug/2023:09:56:36 0800] "GET /FS_WEB_ASS/webim_api/socket/message HTTP/1.1" 403 5 "-" "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit…...

编程日记 2023/8/22 2:28:41

websocker无法注入依赖

在公司中准备用websocker统计在线人数&#xff0c;在WebSocketServer使用StringRedisTemplate保存数据到redis中去&#xff0c;但是在保存的时候显示 StringRedisTemplate变量为null 详细问题 2023-08-20 10:37:14.109 ERROR 28240 --- [nio-7125-exec-1] o.a.t.websocket.po…...

编程日记 2023/8/22 2:27:40

如何进行无线网络渗透测试？

我们将重点介绍如何使用Kali Linux进行无线网络渗透测试。无线网络渗透测试是评估无线网络安全性的重要步骤&#xff0c;而Kali Linux作为一款专业的渗透测试发行版&#xff0c;提供了丰富的工具来进行这项任务。 1. 准备工作 在开始无线网络渗透测试之前&#xff0c;有一些准…...

编程日记 2023/8/22 2:26:39

【Python机器学习】实验15 将Lenet5应用于Cifar10数据集（PyTorch实现）

文章目录 CIFAR10数据集介绍1. 数据的下载2.修改模型与前面的参数设置保持一致3. 新建模型4. 从数据集中分批量读取数据5. 定义损失函数6. 定义优化器7. 开始训练8.测试模型 9. 手写体图片的可视化10. 多幅图片的可视化 思考题11. 读取测试集的图片预测值&#xff08;神经网络的…...

编程日记 2023/8/22 2:25:38

Jeep车型数据源：提供Jeep品牌车系、车型、价格、配置等信息

​​​​​ Jeep是一个极具特色的汽车品牌&#xff0c;它的所有车型都注重实用性&#xff0c;具有越野性能和高性能。Jeep品牌在汽车行业中的口碑一直是非常不错的。如果你想要了解Jeep品牌车系、车型、价格、配置等信息&#xff0c;就可以通过挖数据平台Jeep车型数据源API接口…...

编程日记 2023/8/22 2:24:37

clickhouse-备份恢复

一、简介 备份恢复是数据库常用的手段&#xff0c;可能大多数公司很少会对大数据所使用的数据进行备份&#xff0c;这里还是了解下比较好&#xff0c;下面做了一些简单的介绍&#xff0c;详细情况可以通过官网来查看&#xff0c;经过测试发现Disk中增量备份并不好用&#xff0…...

编程日记 2023/8/22 2:23:34

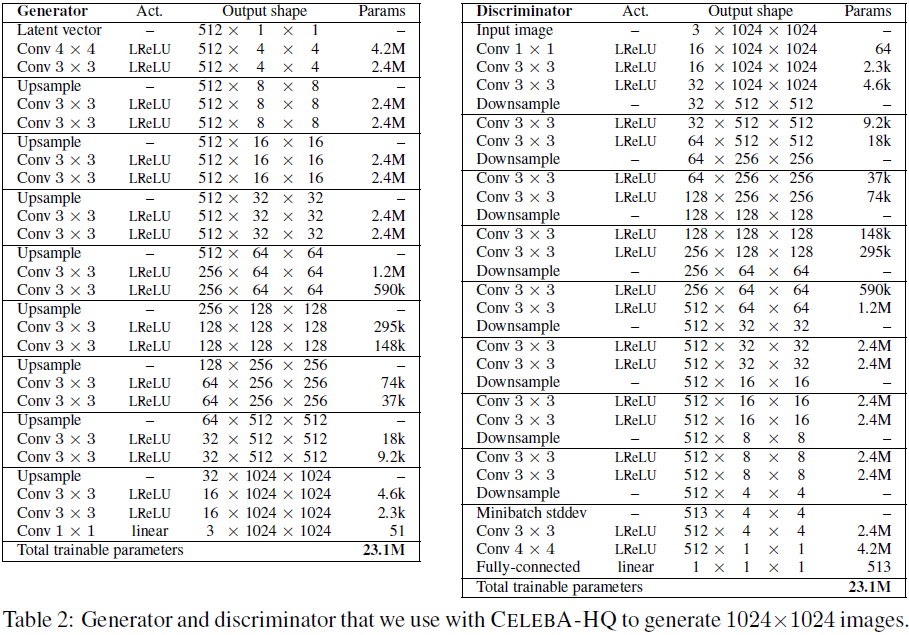
（2018，ProGAN）渐进式发展 GAN 以提高质量、稳定性和变化

Progressive Growing of GANs for Improved Quality, Stability, and Variation 公众号&#xff1a;EDPJ 目录 0. 摘要 1. 简介 2. GAN 的渐进式发展 3. 使用小批量标准差增加变化 4. 生成器和判别器的归一化 4.1 均衡学习率 4.2 生成器中的像素特征向量归一化 5. 评…...

编程日记 2023/8/22 2:22:33

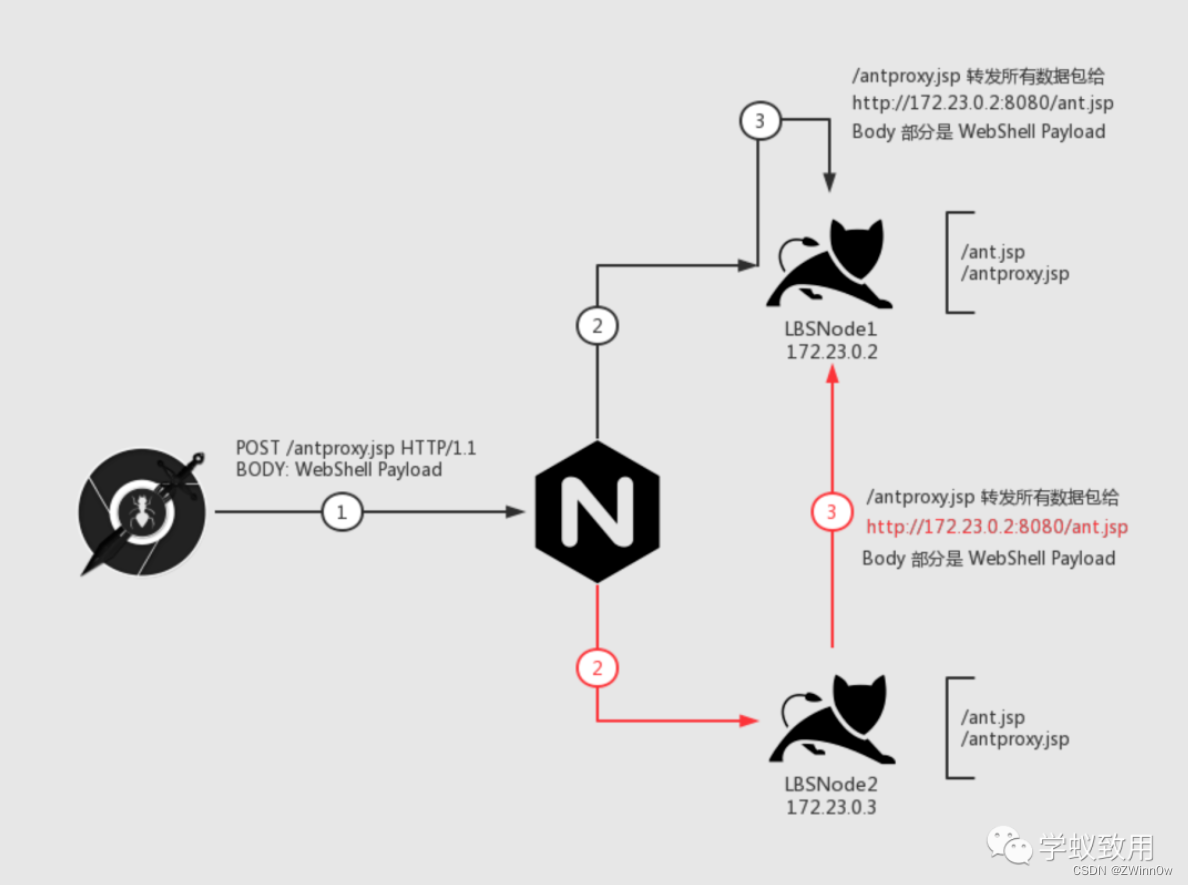
负载均衡下的 WebShell 连接

目录 负载均衡简介负载均衡的分类网络通信分类 负载均衡下的 WebShell 连接场景描述难点介绍解决方法**Plan A** **关掉其中一台机器**&#xff08;作死&#xff09;**Plan B** **执行前先判断要不要执行****Plan C** 在Web 层做一次 HTTP 流量转发 &#xff08;重点&#xff0…...

编程日记 2023/8/22 2:21:29

Postman的高级用法—Runner的使用​

1.首先在postman新建要批量运行的接口文件夹&#xff0c;新建一个接口&#xff0c;并设置好全局变量。 2.然后在Test里面设置好要断言的方法 如&#xff1a; tests["Status code is 200"] responseCode.code 200; tests["Response time is less than 10000…...

编程日记 2023/8/22 2:20:28

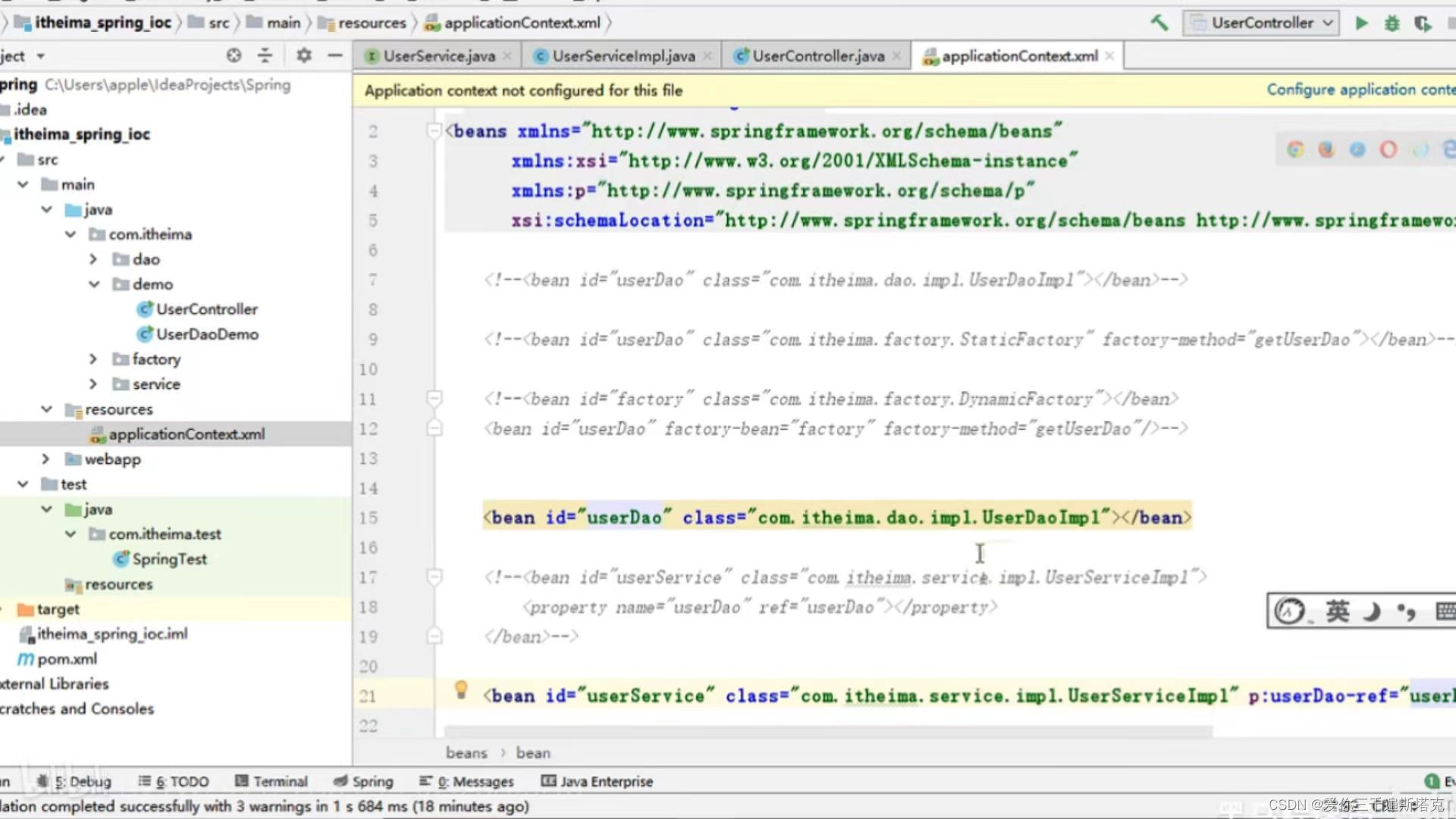
spring如何进行依赖注入，通过set方法把Dao注入到serves

1、选择Generate右键鼠标 你在service层后面方法的这些: 2、UserService配置文件的写法是怎样的&#xff1a; 3、我们在UserController中执行一下具体写法&#xff1a; 最后我们执行一下 &#xff1a; 4、这里可能出现空指针&#xff0c;因为你当前web层,因为你new这个对象根…...

编程日记 2023/8/22 2:19:26

Python使用图像处理库PIL（Python Imaging Library）和NumPy库来比较两副图像的相似度

目录 1、解释说明&#xff1a; 2、使用示例&#xff1a; 3、注意事项&#xff1a; 1、解释说明&#xff1a; 在Python中&#xff0c;我们可以使用图像处理库PIL&#xff08;Python Imaging Library&#xff09;和NumPy库来比较两副图像的相似度。常用的图像相似度计算方法有…...

编程日记 2023/8/22 2:18:25

clickhouse扩缩容

一、背景 我们之前已经学会了搭建clickhouse集群&#xff0c;我们搭建的是一套单分片两副本的集群&#xff0c;接下来我们来测试下clickhouse的扩缩容情况 二、扩容 扩容相对来说比较简单&#xff0c;我们原来的架构如下 hostshardreplica192.169.1.111192.169.1.212 现在…...

编程日记 2023/8/22 2:17:23

动漫3D虚拟人物制作为企业数字化转型提供强大动力

一个 3D 虚拟数字人角色的制作流程&#xff0c;可以分为概念设定-3D 建模-贴图-蒙皮-动画-引擎测试六个步骤&#xff0c;涉及到的岗位有原画师、模型师、动画师等。角色概念设定、贴图绘制一般是由视觉设计师来完成;而建模、装配(骨骼绑定)、渲染动画是由三维设计师来制作完成。…...

编程日记 2023/8/22 2:16:21

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2026/2/7 9:51:41

3.3.1_1 检错编码（奇偶校验码）

从这节课开始&#xff0c;我们会探讨数据链路层的差错控制功能&#xff0c;差错控制功能的主要目标是要发现并且解决一个帧内部的位错误&#xff0c;我们需要使用特殊的编码技术去发现帧内部的位错误&#xff0c;当我们发现位错误之后&#xff0c;通常来说有两种解决方案。第一…...

编程新知 2026/1/30 3:28:14

【磁盘】每天掌握一个Linux命令 - iostat

目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat&#xff08;I/O Statistics&#xff09;是Linux系统下用于监视系统输入输出设备和CPU使…...

编程新知 2025/9/30 16:39:11

电脑插入多块移动硬盘后经常出现卡顿和蓝屏

当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时&#xff0c;可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案&#xff1a; 1. 检查电源供电问题 问题原因&#xff1a;多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

编程新知 2025/10/28 15:02:57

工程地质软件市场：发展现状、趋势与策略建议

一、引言 在工程建设领域&#xff0c;准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具&#xff0c;正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

编程新知 2025/10/6 6:10:29

【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张（Windows/Linux）

要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况&#xff0c;可以通过以下几种方式模拟或触发&#xff1a; 1. 增加CPU负载 运行大量计算密集型任务&#xff0c;例如&#xff1a; 使用多线程循环执行复杂计算&#xff08;如数学运算、加密解密等&#xff09;。运行图…...

编程新知 2025/11/30 10:30:15

力扣-35.搜索插入位置

题目描述 给定一个排序数组和一个目标值&#xff0c;在数组中找到目标值&#xff0c;并返回其索引。如果目标值不存在于数组中&#xff0c;返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

编程新知 2025/12/3 3:22:43

ABAP设计模式之---“简单设计原则(Simple Design)”

“Simple Design”&#xff08;简单设计&#xff09;是软件开发中的一个重要理念&#xff0c;倡导以最简单的方式实现软件功能&#xff0c;以确保代码清晰易懂、易维护&#xff0c;并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计&#xff0c;遵循“让事情保…...

编程新知 2026/1/27 18:13:23

Unsafe Fileupload篇补充-木马的详细教程与木马分享（中国蚁剑方式）

在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马&#xff08;服务器方面的&#xff09;的原理&#xff0c;连接&#xff0c;以及各种木马及连接工具的分享 文件木马&#xff1a;https://w…...

编程新知 2026/1/25 10:13:29

C++.OpenGL （14/64）多光源（Multiple Lights）

多光源（Multiple Lights） 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

编程新知 2025/6/11 3:15:20