假设检验选择统计量重点-----正态总体参数的假设检验
文章目录
- 单个正态总体参数的假设检验
- 单边检验简介--计算拒绝域
- 两个正态总体参数的假设检验
- 方差已知的两正态总体均值的假设检验
- 均值未知的两正态总体方差的假设检验
单个正态总体参数的假设检验
- 设总体X∼N(μ,σ2)X\sim N(\mu,\sigma^2)X∼N(μ,σ2)
- X1,X2,⋯,XnX_1,X_2,\cdots,X_nX1,X2,⋯,Xn是来自XXX的样本
- 样本均值与样本方差为X‾,S2\overline{X},S^2X,S2
单个正态总体N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的均值μ\muμ的假设检验
此时有两种情况:
- 1.σ2\sigma^2σ2已知(U检验法)
- 2.σ2\sigma^2σ2未知(t检验法)
1.σ2\sigma^2σ2已知(U检验法)
- 关于双边检验:H0:μ=μ0,H1:μ≠μ0H_0:\mu=\mu_0,H_1:\mu\ne\mu_0H0:μ=μ0,H1:μ=μ0
- U检验法的检验统计量为:U=X‾−μ0σ/n∼N(0,1)U=\frac{\overline X - \mu_0}{\sigma/\sqrt{n}}\sim N(0,1)U=σ/nX−μ0∼N(0,1)
- 知识点:对给定的α\alphaα,μ\muμ的置信度为1−α1-\alpha1−α的置信区间计算过程为:P(∣X‾−μσ/n∣<zα2)=1−αP(|\frac{\overline X - \mu}{\sigma/\sqrt{n}}|<z_{\frac{\alpha}2})=1-\alphaP(∣σ/nX−μ∣<z2α)=1−α
- 即P(X‾−σnzα2<μ<X‾+σnzα2)=1−αP(\overline X-\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2}<\mu<\overline X+\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2})=1-\alphaP(X−nσz2α<μ<X+nσz2α)=1−α
- 所以总体均值μ\muμ的置信度为1−α1-\alpha1−α的置信区间为(X‾−σnzα2,X‾+σnzα2)(\overline X-\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2},\overline X+\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2})(X−nσz2α,X+nσz2α)
- so,回答这个标题下的问题,H0H_0H0的拒绝域应该为(−∞,X‾−σnzα2)∪(X‾+σnzα2,+∞)(-\infty,\overline X-\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2})\cup(\overline X+\frac{\sigma}{\sqrt n}z_{\frac{\alpha}2},+\infty)(−∞,X−nσz2α)∪(X+nσz2α,+∞)
单个正态总体方差的假设检验
单边检验简介–计算拒绝域
两个正态总体参数的假设检验
方差已知的两正态总体均值的假设检验
均值未知的两正态总体方差的假设检验
相关文章:

假设检验选择统计量重点-----正态总体参数的假设检验
文章目录单个正态总体参数的假设检验单个正态总体N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的均值μ\muμ的假设检验1.σ2\sigma^2σ2已知(U检验法)单个正态总体方差的假设检验单边检验简介--计算拒绝域两个正态总体参数的假设检验方差已知的两正态总体均值的假设检验均值未知的两正态…...
 | 机试题算法思路 【2023】)
华为OD机试 - 通信误码(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 自动曝光(Python) | 机试题算法思路 【2023】 华为OD机试 - 双十一(Python) | 机试题算法思路 【2023】 华为OD机试 - 删除最少字符(Python) | 机试题算法思路 【2023-02】 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 …...

设计模式之装饰者模式
文章の目录一、什么是装饰者模式二、优势三、缺点四、应用场景五、示例参考写在最后一、什么是装饰者模式 装饰者模式也称为包装器模式,在不改变原有对象的基础上为其动态的添加上新的功能。 装饰者模式有以下特点: 添加功能时不改变原对象结构。装饰…...
【第31天】SQL进阶-写优化- 插入优化(SQL 小虚竹)
回城传送–》《31天SQL筑基》 文章目录零、前言一、练习题目二、SQL思路:SQL进阶-写优化-插入优化解法插入优化禁用索引语法如下适用数据库引擎非空表:禁用索引禁用唯一性检查语法如下适用数据库引擎禁用外键检查语法如下适用数据库引擎批量插入数据语法…...
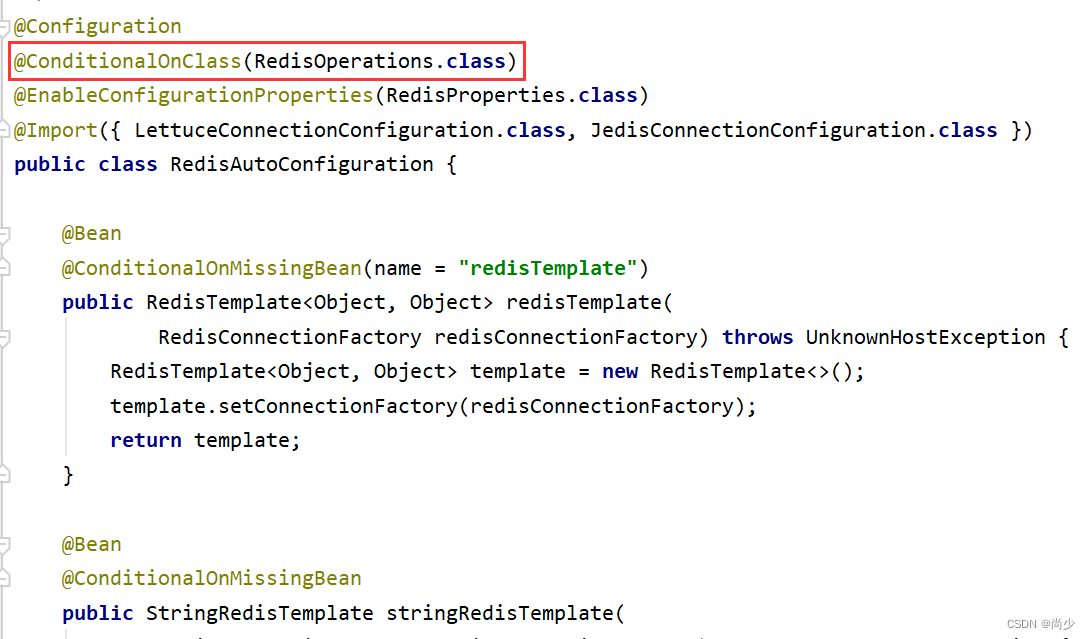
SpringBoot自动装配的原理
前言 在开发SpringBoot项目时,当我们引入spring-boot-starter-xxx依赖后,想要使用依赖中的bean,直接就用Autowired拿来用了,不需要用xml或者注解的方式把它先注入到Spring容器中。这就是自动装配的特性,本文来讲述Spri…...
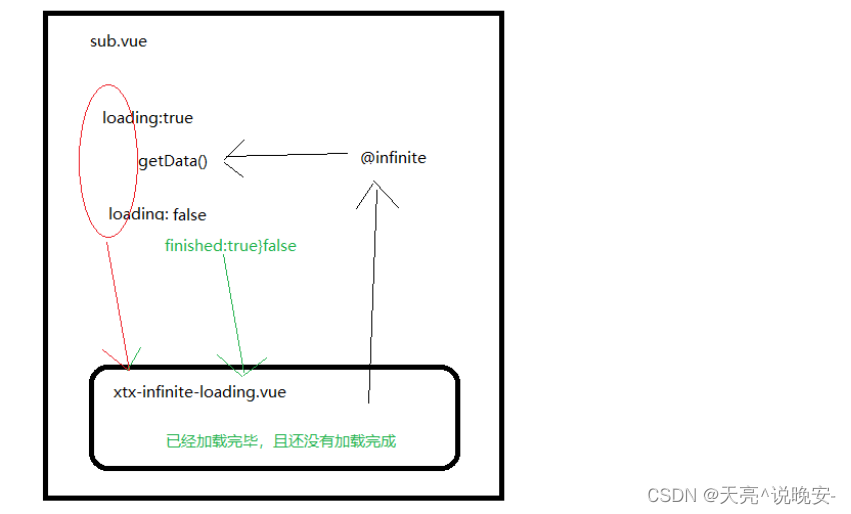
Vue3电商项目实战-分类模块5【12-二级类目-结果区-排序组件、13-二级类目-结果区-数据加载、14-二级类目-结果区-进行筛选】
文章目录12-二级类目-结果区-排序组件13-二级类目-结果区-数据加载14-二级类目-结果区-进行筛选12-二级类目-结果区-排序组件 目的:封装排序组件,完成排序切换效果 大致步骤: 定义一个组件 sub-sort,完成基础布局在 sub.vue 组件…...

计算机操作系统概述
文章目录1.0 操作系统概述1.1 操作系统的目标1.2 操作系统的功能1.3 操作系统结构1.4 操作系统接口1.5 操作系统的发展1.6 操作系统的特征2.0 进程管理2.1 进程调度2.2 进程调度算法2.3 进程间通信2.4 进程间的同步2.5 软件实现互斥的方法2.6 硬件实现互斥的方法2.7 信号2.8 管…...
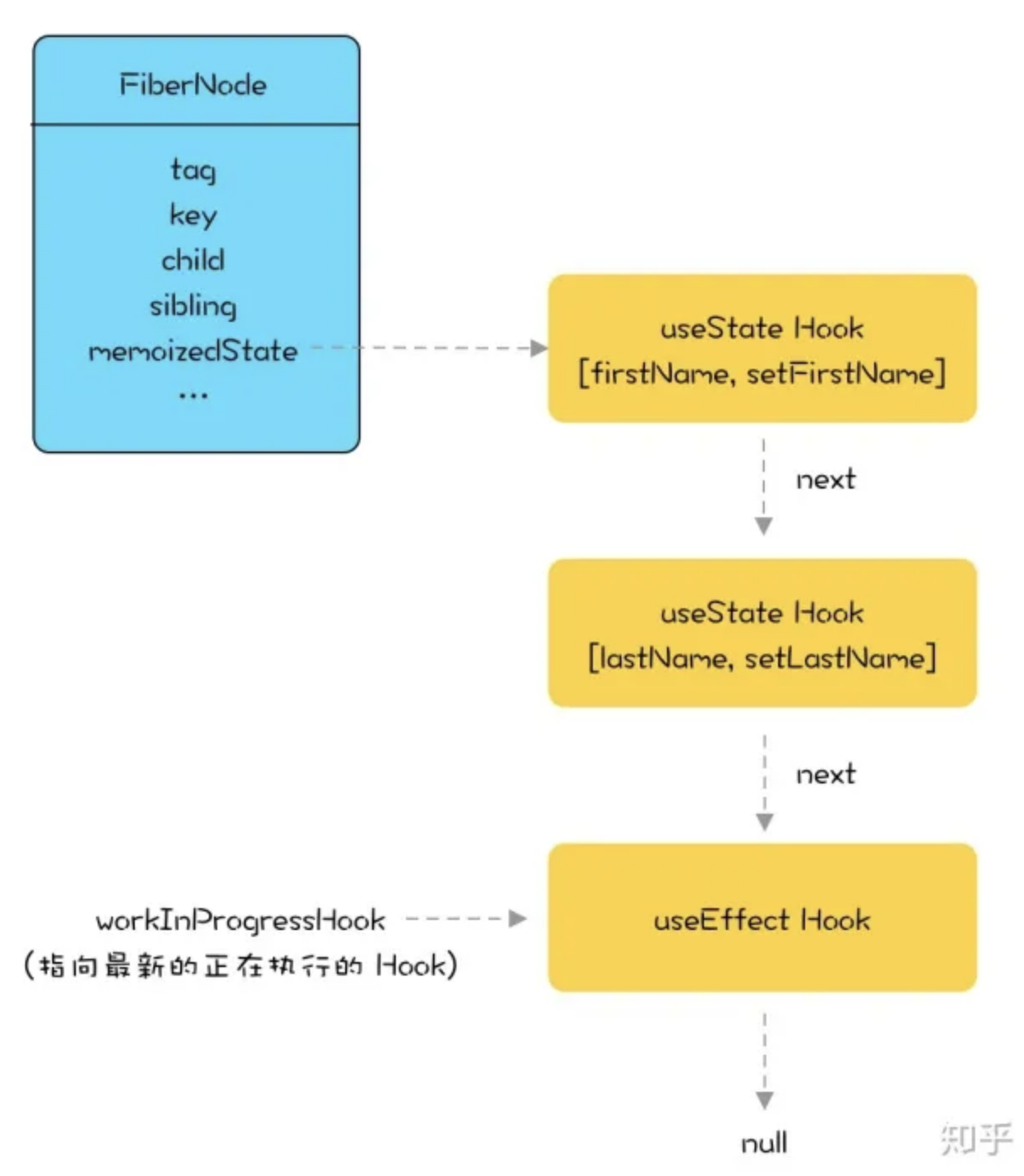
面试官让你说说react状态管理?
hooks 为什么不能放在条件判断里 以 setState 为例,在 react 内部,每个组件(Fiber)的 hooks 都是以链表的形式存在 memoizeState 属性中 update 阶段,每次调用 setState,链表就会执行 next 向后移动一步。如果将 setState 写在条…...

CUDA线程块的分配
为了确保能够真正地了解线程块的分配,接下来我们写一个简短的内核程序来输出线程块、线程、线程束和线程全局标号到屏幕上。现在,除非你使用的是 3.2 版本以上的 SDK否则内核中是不支持 printf的。因此,我们可以将数据传送回 CPU 端然后输出到…...
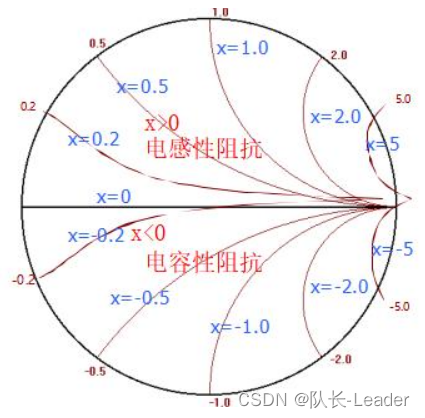
史密斯圆图
在射频、微波中,常常使用史密斯圆图来做阻抗匹配。在不涉及复杂的数学推导,仍能把圆图用起来。 比如,共轭匹配。 RL1jX,需要找到-jX来抵消jX,消掉虚部之后,只留下实部,最终等效为RL‘1。 史密…...
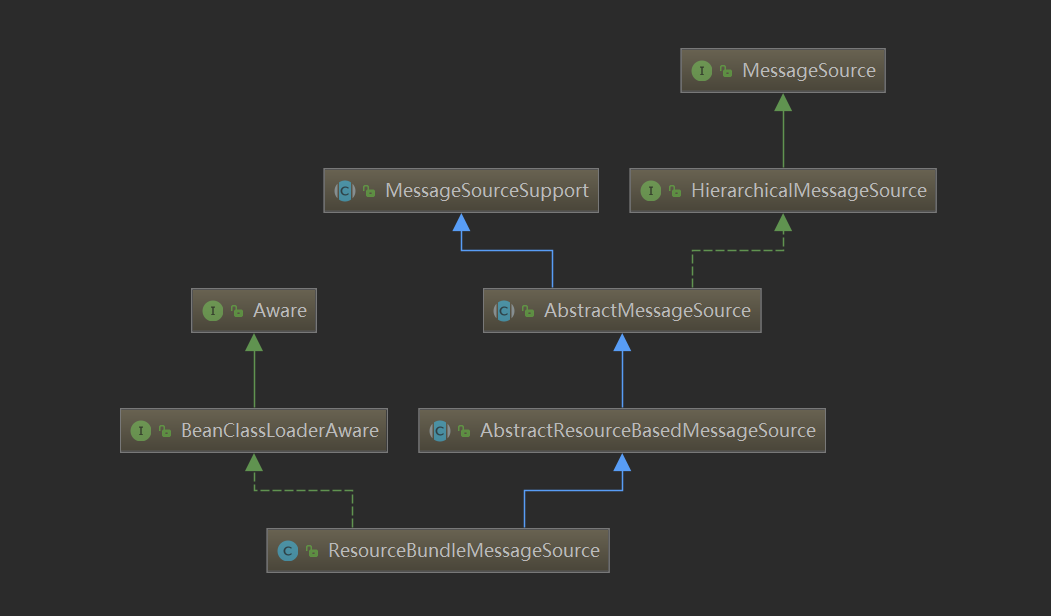
Spring国际化实现
Java国际化 Java使用Unicode来处理所有字符。 Locales 国际化主要涉及的是数字、日期、金额等。 有若干个专门负责格式处理的类。为了对格式进行控制,可以使用Locale类。它描述了: 一种语言一个位置(通常包含)一段脚本(可选,自Java SE7开…...
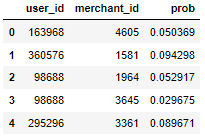
10- 天猫用户复购预测 (机器学习集成算法) (项目十) *
项目难点 merchant: 商人重命名列名: user_log.rename(columns{seller_id:merchant_id}, inplaceTrue)数据类型转换: user_log[item_id] user_log[item_id].astype(int32)主要使用方法: xgboost, lightbm竞赛地址: 天猫复购预测之挑战Baseline_学习赛_天池大赛-阿里云天池…...

对于《MySQL 实战45讲》的理解
一.理论 一条SQL执行过程 连接器分析器优化器执行器 索引 索引的出现其实就是为了提高数据查询的效率,就像书的目录一样 常见索引数据结构(每碰到一个新数据库,我们需要先关注它的数据模型,这样才能从理论上分析出这个数据库的适用场景) 哈希…...

XQuery 函数
XQuery 1.0、XPath 2.0 以及 XSLT 2.0 共享相同的函数库。 XQuery 函数 XQuery 含有超过 100 个内建的函数。这些函数可用于字符串值、数值、日期以及时间比较、节点和 QName 操作、序列操作、逻辑值等等。您也可在 XQuery 中定义自己的函数。 XQuery 内建函数 XQuery 函数命…...
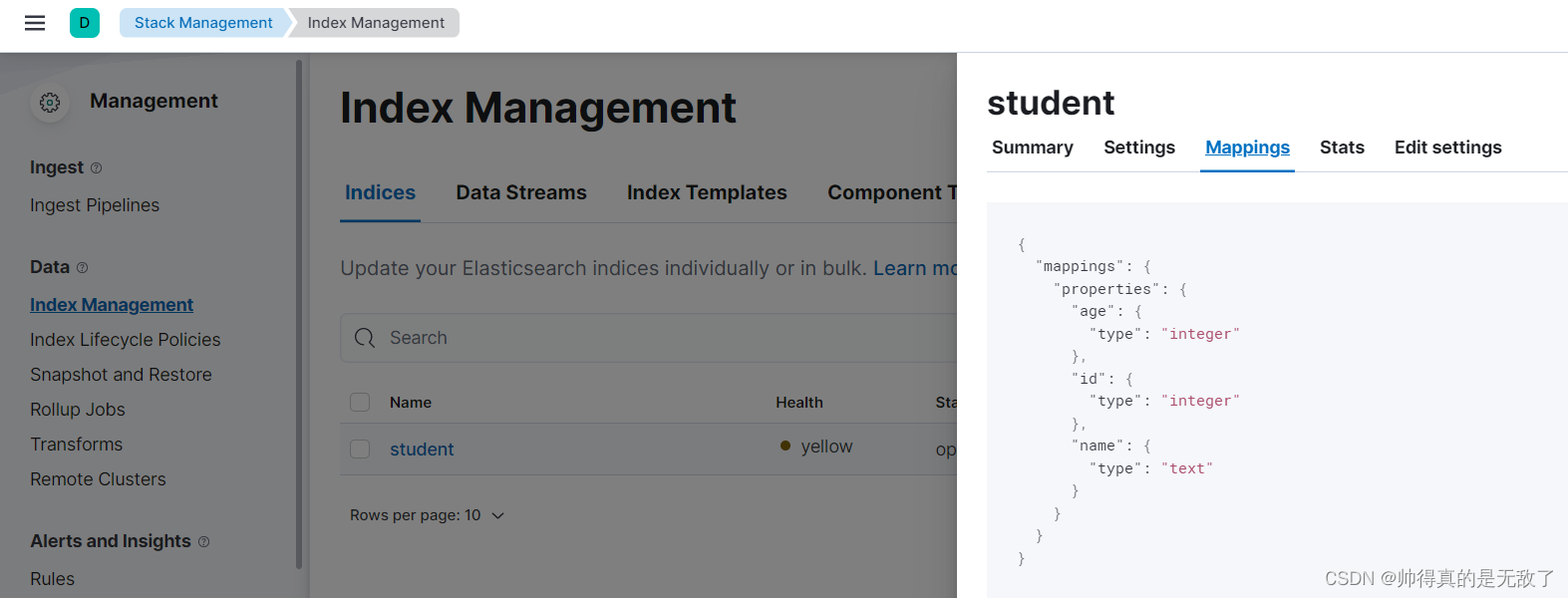
Elasticsearch的安装及常用操作
文章目录一、Elasticsearch的介绍1、Elasticsearch索引2、Elasticsearch的介绍二、Elasticsearch的安装1、安装ES服务2、安装kibana3、Docker安装ES4、Docker安装Kibana三、ES的常用操作1、索引操作2、文档操作3、域的属性3.1 index3.2 type3.3 store总结一、Elasticsearch的介…...
网络安全应急响应服务方案怎么写?包含哪些阶段?一文带你了解!
文章目录一、服务范围及流程1.1 服务范围1.2 服务流程及内容二、准备阶段2.1 负责人准备内容2.2 技术人员准备内容(一)服务需求界定(二)主机和网络设备安全初始化快照和备份2.3市场人员准备内容(1)预防和预…...

11、事务原理和实战,MVCC
事务原理和实战 1. 认识事务2. 事务控制语句2.1 开启事务2.2 事务提交2.3 事务回滚3. 事务的实现方式3.1 原子性3.2 一致性3.3 隔离性3.3 持久性4purge thread线程5事务统计QPS与TPS5.1 QPS5.2 TPS6. 事务隔离级别6.1 隔离级别6.2 查看隔离级别6.3 设置隔离级别6.4 不同隔离级别…...
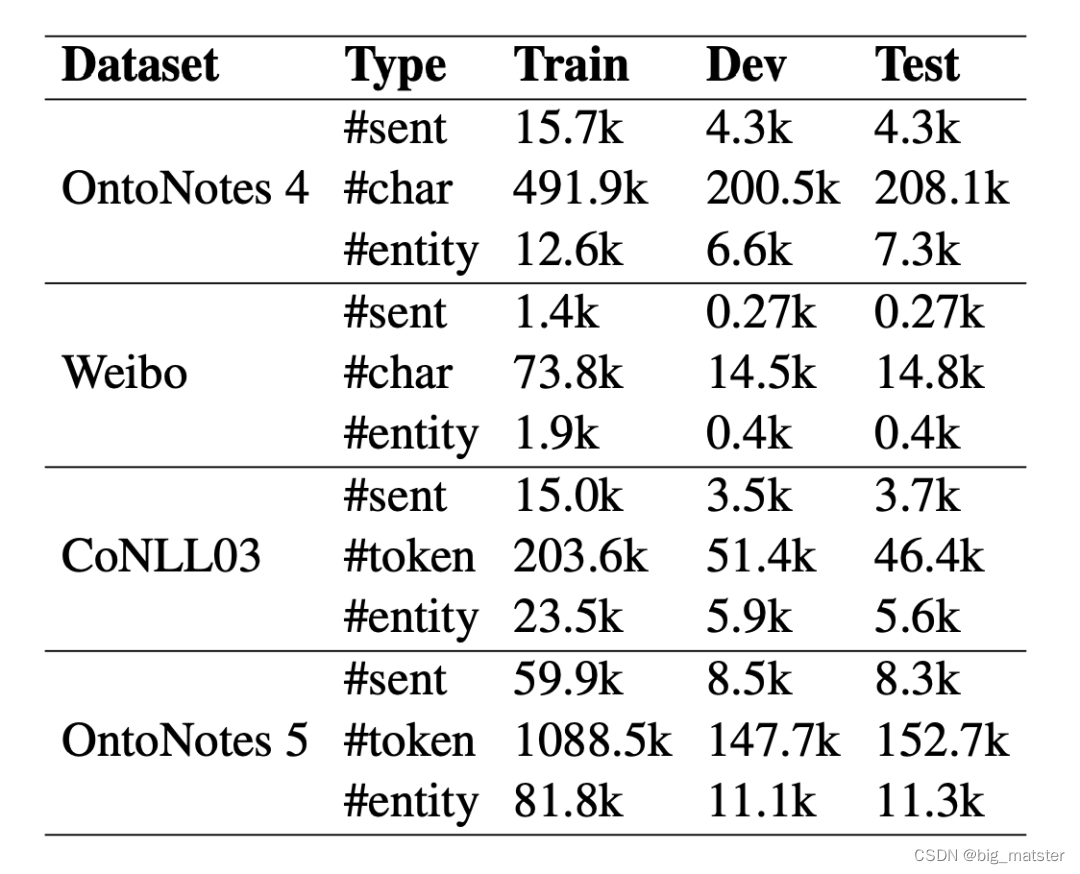
Robust Self-Augmentation for Named Entity Recognition with Meta Reweighting
摘要 近年来,自我增强成为在低资源场景下提升命名实体识别性能的研究热点。Token substitution and mixup (token替换和表征混合)是两种有效提升NER性能的自增强方法。明显,自增强方法得到的增强数据可能由潜在的噪声。先前的研究…...

Java基础-xml
1.xml 1.1概述 万维网联盟(W3C) 万维网联盟(W3C)创建于1994年,又称W3C理事会。1994年10月在麻省理工学院计算机科学实验室成立。 建立者: Tim Berners-Lee (蒂姆伯纳斯李)。 是Web技术领域最具权威和影响力的国际中立性技术标准机构。 到目前为止&#…...

TCP的Nagle算法和delayed ack---延时发送和延时应答与稍带应答选项
本文目录提高TCP的网络利用率的二个思考解决方案:Nagle算法和delayed ack(延时发送和延时应答与稍带应答选项)Nagle算法和delayed ack算法同时启动可能会导致的问题提高TCP的网络利用率的二个思考 我们都知道,TCP是一个基于字节流…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
