Java-算法竞赛中常用的Java API之大数类
Java-算法竞赛中常用的Java API之大数类
- 摘要
- BigInteger和BigDecimal
- 创建
- 赋值
- 加法
- 减法
- 乘法
- 除法
- *取余
- *求最大公因数
- 求最值
- *(a^b)%mod
- 比较大小
- *进制转化
- 类型转化
- BigDecimal精度问题
- 保留n位小数
摘要
java中的基础数据类型能存储的最大的二进制数是 2 ^ 63 - 1,
对应的十进制数是9223372036854775807,也就是说只要运算过程中会超过这个数,就会造成数据溢出,从而造成错误.
1.而java.math.*包中提供了大数类,其理论上可以存储无限位的大数,只要内存足够的话。
2.大数类又分为整数和浮点数.即BigInteger and BigDecimal。
3.大数类的对象不能直接进行运算,需要调用类中相应的方法,并且方法的参数4必须和调用的类相同,BigInteger不能调用BigDecimal, 不能作为其方法参数, 即整数和浮点数不能混合运算.。
4.本文举例了一些常用的方法,不需要背会,需要用的时候查java API就行了。
BigInteger和BigDecimal
创建
//1.直接声明
BigInteger a;
BigDecimal b;
//2.使用构造函数初始化
BigInteger a = new BigInteger("123456789101112131415");
BigDecimal b = new BigDecimal("123456.123456");赋值
BigInteger.valueOf(long val);
BigDecimal.valueOf(double val);
BigInteger a;
BigDecimal b;
//注意 val 不能超过 long 类型的最大取值9223372036854775807, 超过int时要在数后面加L如:
a = BigInteger.valueOf(123456789101112L); //大于int范围的要加L
b = BigDecimal.valueOf(123456.12341235); // 超出的小数位数会自动舍弃 使用 = 将同类型变量的值赋给另一个变量
BigInteger a;
BigInteger b = new BigInteger("123456");
a = b;
System.out.print(a);输出:
123456加法
BigInteger.add(BigInteger);
BigDecimal.add(BigDecimal);
BigInteger a, b, c;
a = BigInteger.valueOf(123456789); // 赋值为 123456789
b = BigInteger.valueOf(987654321); // 赋值为 987654321
c = a.add(b);
System.out.print(c);
输出:
1111111110
1111111110 减法
BigInteger.subtract(BigInteger);
BigDecimal.sbutract(BigDecimal);
BigInteger a, b, c;
a = BigInteger.valueOf(123456789); // 赋值为 123456789
b = BigInteger.valueOf(987654321); // 赋值为 987654321
c = a.subtract(b);
System.out.print(c);输出:
-864197532乘法
BigInteger.multiply(BigInteger);
BigDecimal.multiply(BigDecimal);
BigInteger a, b, c;
a = BigInteger.valueOf(123456789); // 赋值为 123456789
b = BigInteger.valueOf(987654321); // 赋值为 987654321
c = a.multiply(b);
System.out.print(c);输出:
121932631112635269除法
BigInteger.divide(BigInteger);
BigDecimal.divide(BigDecimal);
BigInteger a, b, c;
a = BigInteger.valueOf(987654321); // 赋值为 987654321
b = BigInteger.valueOf(123456789); // 赋值为 123456789
c = a.divide(b); // 整数相除仍为整数
System.out.print(c);输出:
8*取余
BigInteger.mod(BigInteger);
BigInteger a, b, c;
a = BigInteger.valueOf(987654321); // 赋值为 987654321
b = BigInteger.valueOf(123456789); // 赋值为 123456789
c = a.mod(b);
System.out.print(c);输出:
9*求最大公因数
BigInteger.gcd(BigInteger);
BigInteger a, b, c;
a = BigInteger.valueOf(987654321); // 赋值为 987654321
b = BigInteger.valueOf(123456789); // 赋值为 123456789
c = a.gcd(b);
System.out.print(c);输出:
9求最值
BigInteger.max(BigInteger) , BigDecimal.max(BigDecimal) 最大值
BigInteger.min(BigInteger) , BigDecimal.min(BigDecimal) 最小值
BigInteger a, b, c, d;
a = BigInteger.valueOf(987654321); // 赋值为 987654321
b = BigInteger.valueOf(123456789); // 赋值为 123456789
c = a.max(b); //a,b中的最大值
d = a.min(b); //a,b中的最小值
System.out.println(c);
System.out.println(d);输出:
987654321
123456789*(a^b)%mod
BigInteger.modPow(BigInteger, BigInteger);
BigInteger a, b, c, mod;
a = BigInteger.valueOf(987654321); // 赋值为 987654321
b = BigInteger.valueOf(123456789); // 赋值为 123456789
mod = BigInteger.valueOf(10007);
c = a.modPow(b, mod); //(a^b)%mod
System.out.println(c);
输出:
718比较大小
BigInteger.compareTo(BigInteger);
BigDecimal.compareTo(BigDecimal);
BigInteger a, b;
int c;
a = BigInteger.valueOf(987654321); // 赋值为 987654321
b = BigInteger.valueOf(123456789); // 赋值为 123456789
c = a.compareTo(b); // a 和 b
System.out.println(c);
c = b.compareTo(b); // b 和 b
System.out.println(c);
c = b.compareTo(a); // c 和 c
System.out.println(c);
输出:
1
0
-1可见, 对于a.compareTo(b), a和b进行比较如果:
a > b 返回 1
a == b 返回 0
a < b 返回-1
*进制转化
使用构造函数BigInteger(String, int index);可以把一个index进制的字符串,转化为10进制的BigInteger;
BigInteger a = new BigInteger("111110", 2);把111110变为10进制赋值给a
System.out.println(a.toString(16));把a转化为16进制的字符串输出类型转化
BigInteger.toBigDecimal() //把BigInteger 转化为 BigDecimal
BigDecimal.toBigInteger() //把BigDecimal 转化为 BigInteger
BigInteger a = new BigInteger(1);BigDecimal b = new BigDecimal(2);b.toBigInteger(); // 把BigDecimal转为BigIntegera.toBigDecimal(); // 把BigInteger转为BigDecimalBigDecimal精度问题
BigDecimal的舍入模式
想象一个数轴,从负无穷到正无穷,向哪舍入,就是趋向于哪, 向0就是舍入后要更趋近于0.
ROUND_DOWN 向零舍入。 即1.55 变为 1.5 , -1.55 变为-1.5
ROUND_CEILING 向正无穷舍入. 即 1.55 变为 1.6 , -1.55 变为 -1.5
ROUND_FLOOR 向负无穷舍入. 即 1.55 变为 1.5 , -1.55 变为 -1.6
ROUND_HALF_UP 四舍五入 即1.55 变为1.6, -1.55变为-1.6
ROUND_HALF_DOWN 五舍六入 即 1.55 变为 1.5, -1.5变为-1.5
ROUND_HALF_EVEN 如果舍入前一位的数字为偶数,则采用HALF_DOWN奇数则采用HALF_UP 如1.55 采用HALF_UP 1.45采用HALF_DOWN
ROUND_UP 向远离0的方向舍入 即 1.55 变为 1.6 , -1.55 变为-1.6
ROUND_UNNECESSARY 有精确的位数时,不需要舍入
在需要精确舍入的方式时可以使用以上的舍入模式。
(另:Math 类的 ceil()和 floor方法对应普通浮点型的上取整和下取整.)
BigDecimal进行加减乘除时可以进行舍入
如 除法
divide(BigDecimal divisor, int scale, RoundingMode roundingMode) 返回一个
BigDecimal ,其值为 (this / divisor) ,其小数位数为scale。
import java.math.*;
import java.util.*;
import java.io.*;
public class Main{public static void main(String[] args){ BigDecimal a, b, c;a = BigDecimal.valueOf(1.51);b = BigDecimal.valueOf(1.37);c = a.divide(b,100,BigDecimal.ROUND_DOWN);//采用向0舍入并并保留100位小数System.out.println(c);}
}
输出:
1.1021897810218978102189781021897810218978102189781021897810218978102189781021897810218978102189781021保留n位小数
setScale(int newScale, RoundingMode roundingMode);
import java.math.*;
import java.util.*;
import java.io.*;
public class Main{public static void main(String[] args){ BigDecimal a = new BigDecimal("1.10218");a = a.setScale(4,BigDecimal.ROUND_HALF_UP);//四舍五入保留四位小数System.out.println(a);}
}相关文章:

Java-算法竞赛中常用的Java API之大数类
Java-算法竞赛中常用的Java API之大数类摘要BigInteger和BigDecimal创建赋值加法减法乘法除法*取余*求最大公因数求最值*(a^b)%mod比较大小*进制转化类型转化BigDecimal精度问题保留n位小数摘要 java中的基础数据类型能存储的最大的二进制数是 2 ^ 63 - 1, 对应的十进制数是92…...

了解Nginx,这一篇就够了
了解Nginx,这一篇就够了1.Nginx应用场景2.Nginx相关概念正向代理和反向代理负载均衡动静分离3.Nginx配置文件解析全局块events块http块1.Nginx应用场景 HTTP服务器:Nginx本身也是一个静态资源的服务器,当只有静态资源的时候,就可…...

k8s删除pod或deployment
查看pod或者deployment信息 deployment: kubectl get deployment -n 命名空间pod: kubectl get pod -n 命名空间删除pod或者deployment 删除pod: kubectl delete pod <pod名> -n <命名空间>可是,此时你会发现刚刚…...

Visual Studio 2022: 增加对虚幻引擎的支持
自 Visual Studio 2022 发布以来,我们一直专注于为游戏和大型项目开发人员提供一系列生产力和性能改进。今天,我们很高兴与大家分享下一组专门用来提高虚幻引擎开发效率的功能。我们听到并看到了来自你(我们的游戏开发人员)的大量…...

【Python】以邮件的方式定时发送一天的股票分析报告
【Python】以邮件的方式定时发送一天的股票分析报告 文章目录【Python】以邮件的方式定时发送一天的股票分析报告1、Python发送邮件1)EmailSender封装2)可能存在的问题2、jinja2动态渲染html页面3、阿里云OSS搭建图床1)Python上传图片到OSS中…...

mybatis条件构造器(二)
mybatis条件构造器(二) 1 准备工作 1.1 建表sql语句(Emp表) SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0;-- ---------------------------- -- Table structure for emp -- ---------------------------- DROP TABLE IF EXISTS emp; CREATE TABLE emp (EMPNO int NOT NU…...
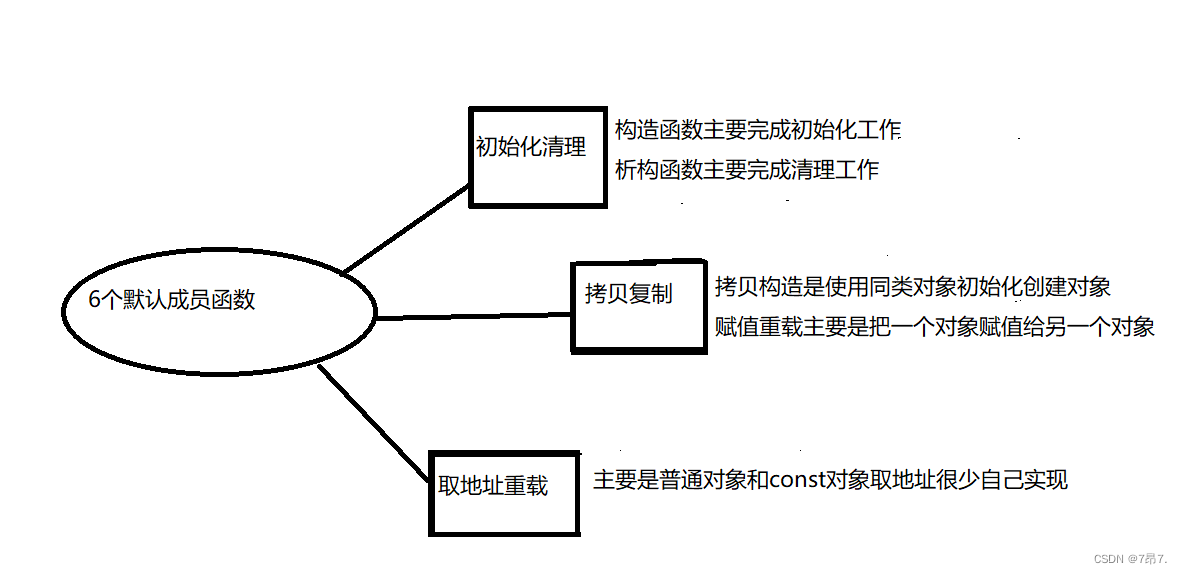
C++【类与对象】
文章目录类与对象(1)类与对象一1.0.面向过程和面向对象初步认识1.1.类的引入1.2.类的定义1.3.类的访问限定符及封装1.4.类的作用域1.5.类的实例化1.6.类的对象大小的计算1.8.类成员函数的this指针(2)类与对象二2.0类的6个默认成员…...

假设检验选择统计量重点-----正态总体参数的假设检验
文章目录单个正态总体参数的假设检验单个正态总体N(μ,σ2)N(\mu,\sigma^2)N(μ,σ2)的均值μ\muμ的假设检验1.σ2\sigma^2σ2已知(U检验法)单个正态总体方差的假设检验单边检验简介--计算拒绝域两个正态总体参数的假设检验方差已知的两正态总体均值的假设检验均值未知的两正态…...
 | 机试题算法思路 【2023】)
华为OD机试 - 通信误码(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 自动曝光(Python) | 机试题算法思路 【2023】 华为OD机试 - 双十一(Python) | 机试题算法思路 【2023】 华为OD机试 - 删除最少字符(Python) | 机试题算法思路 【2023-02】 华为OD机试 - Excel 单元格数值统计(Python) | 机试题算法思路 …...

设计模式之装饰者模式
文章の目录一、什么是装饰者模式二、优势三、缺点四、应用场景五、示例参考写在最后一、什么是装饰者模式 装饰者模式也称为包装器模式,在不改变原有对象的基础上为其动态的添加上新的功能。 装饰者模式有以下特点: 添加功能时不改变原对象结构。装饰…...
【第31天】SQL进阶-写优化- 插入优化(SQL 小虚竹)
回城传送–》《31天SQL筑基》 文章目录零、前言一、练习题目二、SQL思路:SQL进阶-写优化-插入优化解法插入优化禁用索引语法如下适用数据库引擎非空表:禁用索引禁用唯一性检查语法如下适用数据库引擎禁用外键检查语法如下适用数据库引擎批量插入数据语法…...
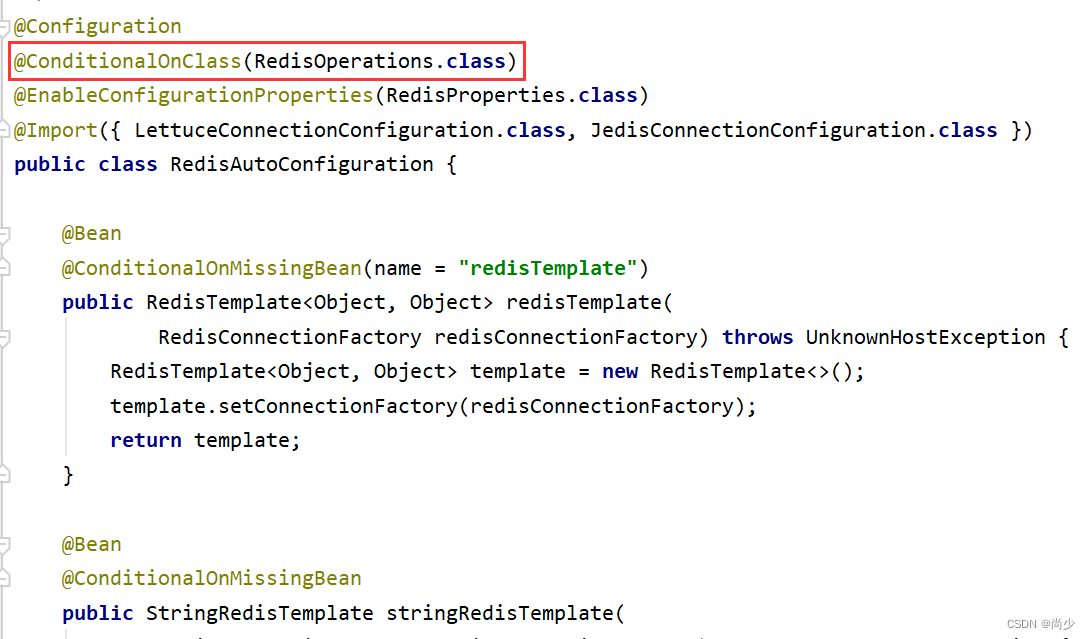
SpringBoot自动装配的原理
前言 在开发SpringBoot项目时,当我们引入spring-boot-starter-xxx依赖后,想要使用依赖中的bean,直接就用Autowired拿来用了,不需要用xml或者注解的方式把它先注入到Spring容器中。这就是自动装配的特性,本文来讲述Spri…...
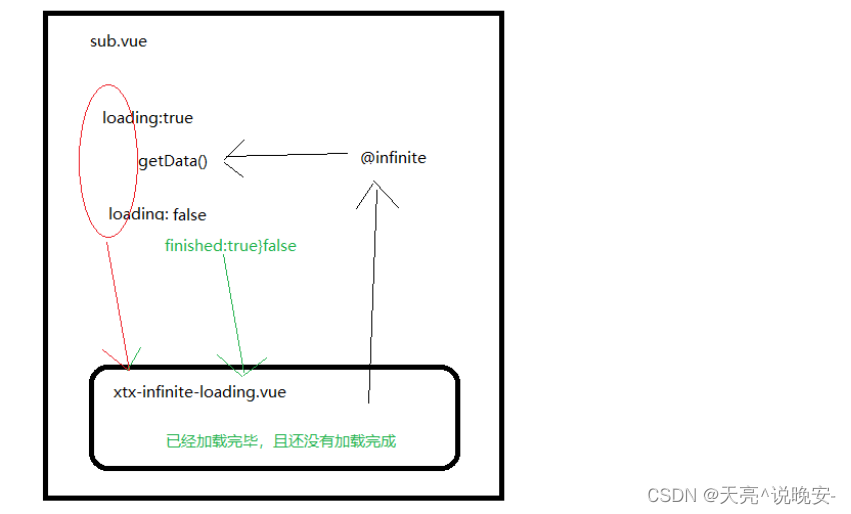
Vue3电商项目实战-分类模块5【12-二级类目-结果区-排序组件、13-二级类目-结果区-数据加载、14-二级类目-结果区-进行筛选】
文章目录12-二级类目-结果区-排序组件13-二级类目-结果区-数据加载14-二级类目-结果区-进行筛选12-二级类目-结果区-排序组件 目的:封装排序组件,完成排序切换效果 大致步骤: 定义一个组件 sub-sort,完成基础布局在 sub.vue 组件…...

计算机操作系统概述
文章目录1.0 操作系统概述1.1 操作系统的目标1.2 操作系统的功能1.3 操作系统结构1.4 操作系统接口1.5 操作系统的发展1.6 操作系统的特征2.0 进程管理2.1 进程调度2.2 进程调度算法2.3 进程间通信2.4 进程间的同步2.5 软件实现互斥的方法2.6 硬件实现互斥的方法2.7 信号2.8 管…...
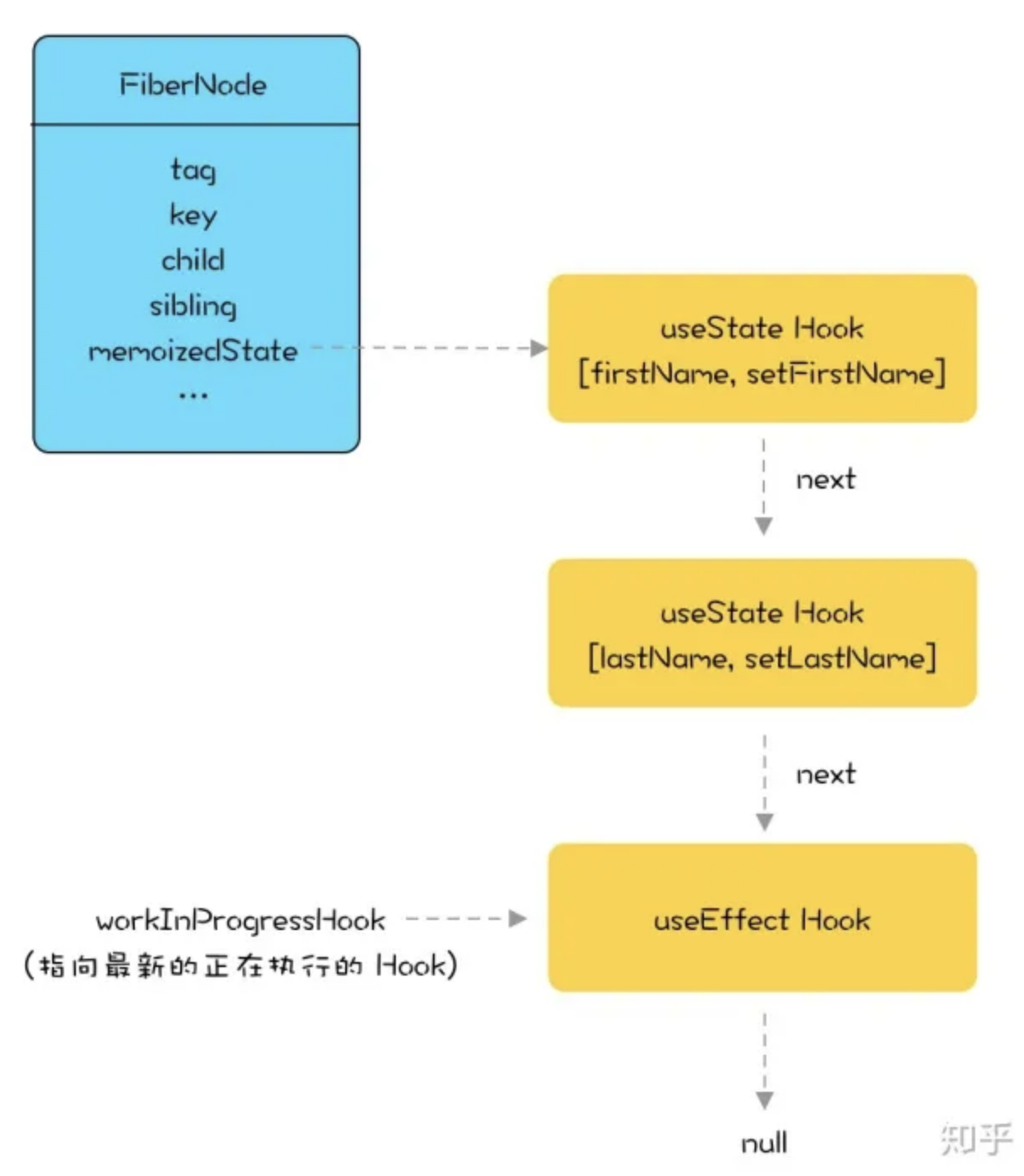
面试官让你说说react状态管理?
hooks 为什么不能放在条件判断里 以 setState 为例,在 react 内部,每个组件(Fiber)的 hooks 都是以链表的形式存在 memoizeState 属性中 update 阶段,每次调用 setState,链表就会执行 next 向后移动一步。如果将 setState 写在条…...

CUDA线程块的分配
为了确保能够真正地了解线程块的分配,接下来我们写一个简短的内核程序来输出线程块、线程、线程束和线程全局标号到屏幕上。现在,除非你使用的是 3.2 版本以上的 SDK否则内核中是不支持 printf的。因此,我们可以将数据传送回 CPU 端然后输出到…...
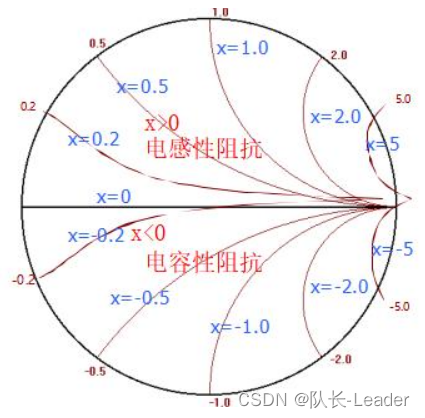
史密斯圆图
在射频、微波中,常常使用史密斯圆图来做阻抗匹配。在不涉及复杂的数学推导,仍能把圆图用起来。 比如,共轭匹配。 RL1jX,需要找到-jX来抵消jX,消掉虚部之后,只留下实部,最终等效为RL‘1。 史密…...
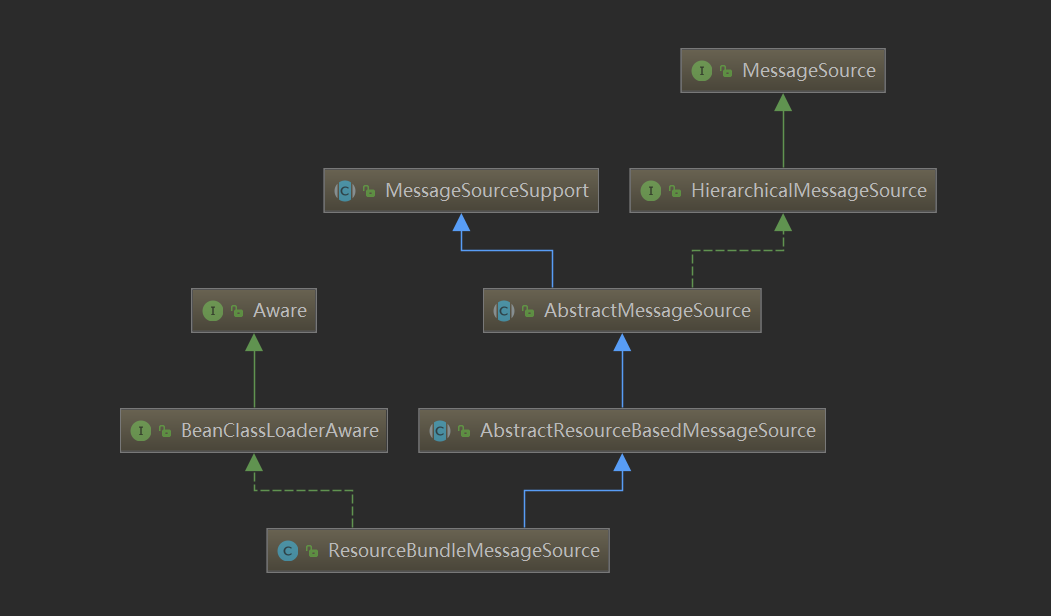
Spring国际化实现
Java国际化 Java使用Unicode来处理所有字符。 Locales 国际化主要涉及的是数字、日期、金额等。 有若干个专门负责格式处理的类。为了对格式进行控制,可以使用Locale类。它描述了: 一种语言一个位置(通常包含)一段脚本(可选,自Java SE7开…...
10- 天猫用户复购预测 (机器学习集成算法) (项目十) *
项目难点 merchant: 商人重命名列名: user_log.rename(columns{seller_id:merchant_id}, inplaceTrue)数据类型转换: user_log[item_id] user_log[item_id].astype(int32)主要使用方法: xgboost, lightbm竞赛地址: 天猫复购预测之挑战Baseline_学习赛_天池大赛-阿里云天池…...

对于《MySQL 实战45讲》的理解
一.理论 一条SQL执行过程 连接器分析器优化器执行器 索引 索引的出现其实就是为了提高数据查询的效率,就像书的目录一样 常见索引数据结构(每碰到一个新数据库,我们需要先关注它的数据模型,这样才能从理论上分析出这个数据库的适用场景) 哈希…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
