原生无限极目录树详细讲解
原生无限级目录树
当涉及到原生的无限级目录树,我们可以使用递归算法来实现。以下是一个使用 JavaScript 实现原生无限级目录树的示例
介绍
原生无限级目录树是一种常见的数据结构,用于组织多层级的目录或分类数据。通过递归算法,我们可以动态地构建和展示这样的目录树结构。
示例代码
// 目录树数据
var data = [{id: 1,name: '目录1',children: [{id: 2,name: '目录1.1',children: [{id: 3,name: '目录1.1.1',children: []},{id: 4,name: '目录1.1.2',children: []}]},{id: 5,name: '目录1.2',children: []}]},{id: 6,name: '目录2',children: []}
];// 渲染目录树
function renderTree(data, container) {// 创建无序列表元素var ul = document.createElement('ul');// 遍历目录树数据for (var i = 0; i < data.length; i++) {var item = data[i];// 创建列表项元素var li = document.createElement('li');// 创建文本节点var textNode = document.createTextNode(item.name);// 将文本节点添加到列表项li.appendChild(textNode);// 如果当前目录项有子目录,则递归渲染子目录if (item.children && item.children.length > 0) {renderTree(item.children, li);}// 将列表项添加到无序列表ul.appendChild(li);}// 将无序列表添加到容器container.appendChild(ul);
}// 获取容器元素
var container = document.getElementById('tree-container');// 渲染目录树
renderTree(data, container);
代码解释
- 定义了一个示例的目录树数据
data,每个目录项包含id、name和children属性。 - 创建
renderTree()函数,用于渲染目录树。 - 在
renderTree()函数中,首先创建一个无序列表元素ul。 - 使用
for循环遍历目录树数据中的每个目录项。 - 创建列表项元素
li,并创建文本节点textNode,将目录项的名称添加到列表项中。 - 如果当前目录项有子目录(即
children属性不为空),则递归调用renderTree()函数,将子目录数据和当前列表项作为参数进行渲染。 - 将列表项
li添加到无序列表ul中。 - 最后,将无序列表
ul添加到指定的容器元素中。
这样,通过递归调用 renderTree() 函数,我们可以将目录树数据动态地渲染为无限级的目录树结构。
相关文章:

原生无限极目录树详细讲解
原生无限级目录树 当涉及到原生的无限级目录树,我们可以使用递归算法来实现。以下是一个使用 JavaScript 实现原生无限级目录树的示例 介绍 原生无限级目录树是一种常见的数据结构,用于组织多层级的目录或分类数据。通过递归算法,我们可以…...

剑指offer(C++)-JZ64:求1+2+3+...+n(算法-位运算)
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 题目描述: 求123...n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句&…...

“深入探究JVM内部机制:如何实现Java程序的运行环境?“
标题:深入探究JVM内部机制:如何实现Java程序的运行环境? 摘要:本文将深入探究Java虚拟机(JVM)的内部机制,重点讨论JVM如何实现Java程序的运行环境。我们将从JVM的结构、类加载、内存管理、垃圾…...

Mac更新homebrew时卡住的解决办法
Mac更新homebrew时卡住的解决办法 引起问题的原因brew命令安装软件跟这3个仓库地址有关1、brew2、homebrew-core3、homebrew-bottles4、若/bin/zsh,则输入5、若/bin/bash,则输入6、更新brew 引起问题的原因 知其然,还要知其所以然。brew的更…...
带你了解—在外远程群晖NAS-群晖Drive挂载电脑磁盘同步备份【无需公网IP】
文章目录 前言1.群晖Synology Drive套件的安装1.1 安装Synology Drive套件1.2 设置Synology Drive套件1.3 局域网内电脑测试和使用 2.使用cpolar远程访问内网Synology Drive2.1 Cpolar云端设置2.2 Cpolar本地设置2.3 测试和使用 3. 结语 前言 群晖作为专业的数据存储中心&…...
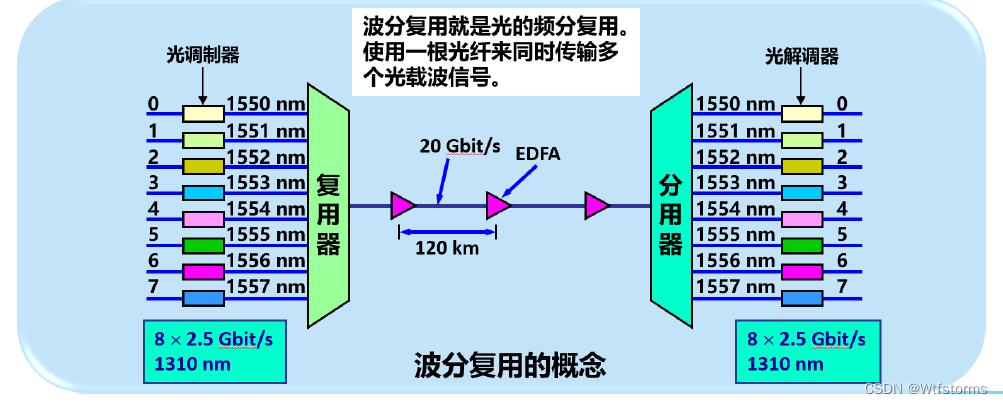
计算机网络第2章(物理层)
计算机网络第2章(物理层) 2.1 物理层的基本概念2.2 物理层下面的传输媒体2.2.1 导引型传输媒体2.2.2 非导引型传输媒体 2.3 传输方式2.3.1 串行传输和并行传输2.3.2 同步传输和异步传输2.3.3 单向通信(单工)、双向交替通信&#x…...

windows钩子保护自身进程不被破坏
代码来自于《windows核心编程》作者: APIHOOK.h头文件: #pragma once #include <Windows.h> class CAPIHOOK { public: CAPIHOOK(LPTSTR lpszModName, LPSTR pszFuncName, PROC pfnHook, BOOL bExcludeAPIHookMod TRUE); ~CAPIHOOK(void); p…...
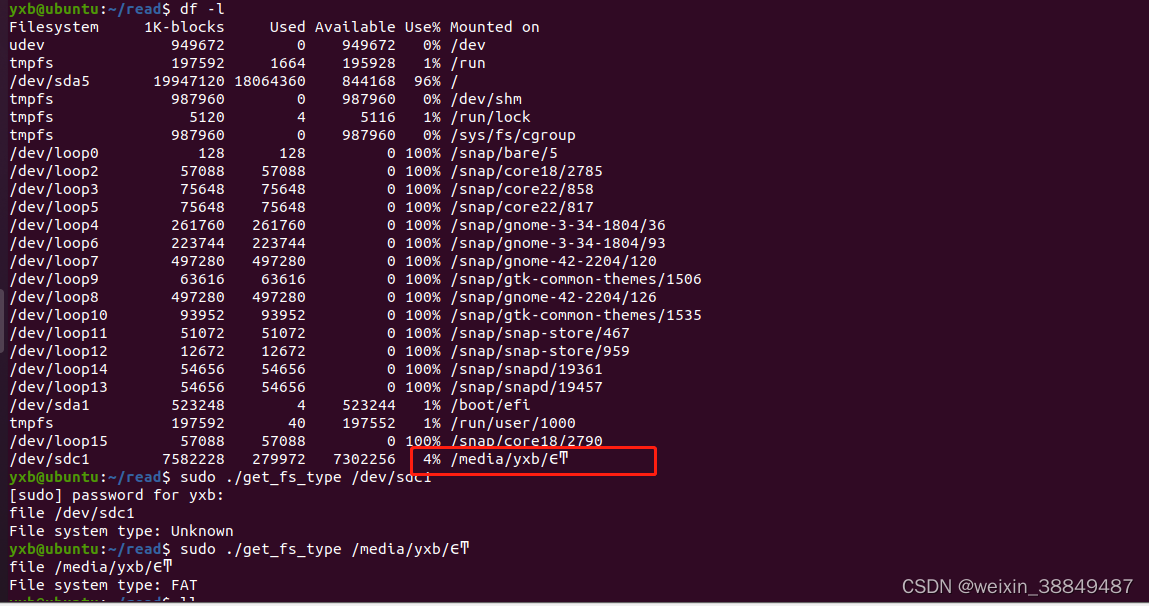
Linux系统查看文件系统类型C代码
系统:VM Ubuntu 实现Linux系统下通过输入指定路径查看文件系统类型,MSDOS_SUPER_MAGIC,NTFS_SUPER_MAGIC和EXT4_SUPER_MAGIC这些宏定义并不是在sys/mount.h中定义的,它们实际上是在linux/magic.h头文件中定义的。不同系统下宏定义可能不一样&…...

Python中的正则表达式
大家好,今天我们将通过详细的解释和代码示例,探讨如何在Python中使用正则表达式。 介绍 正则表达式(regex)是一种用于操作文本和数据的强大工具,它们提供了一种简洁灵活的方式来“匹配”(指定和识别&…...
第六章,创作文章
6.1添加创作页面 <template><div class="blog-container"><div class="blog-pages"><div class="col-md-12 panel"><div class="panel-body"><h2 class="text-center">创作文章&l…...
Win10c盘满了怎么清理?快速清理,5个方法!
“快救救孩子吧!我的电脑是win10系统的,现在c盘满了,根本没法继续使用电脑了。怎么才能快速的释放内存呢?非常着急!感谢大家!” C盘是Windows系统中重要的分区,当其存储空间满了,可能…...

回归预测 | MATLAB实现GWO-BP灰狼算法优化BP神经网络多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现GWO-BP灰狼算法优化BP神经网络多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现GWO-BP灰狼算法优化BP神经网络多输入单输出回归预测(多指标,多图)效果一览基本介绍程序…...

docker 06(docker compose)
一、服务编排 二、docker compose...

非阻塞重试与 Spring Kafka 的集成测试
如何为启用重试和死信发布的消费者的 Spring Kafka 实现编写集成测试。 Kafka 非阻塞重试 Kafka 中的非阻塞重试是通过为主主题配置重试主题来完成的。如果需要,还可以配置其他死信主题。如果所有重试均已用尽,事件将转发至 DLT。公共领域提供了大量资…...
基于 Debian 12 的MX Linux 23 正式发布!
导读MX Linux 是基于 Debian 稳定分支的面向桌面的 Linux 发行,它是 antiX 及早先的 MEPIS Linux 社区合作的产物。它采用 Xfce 作为默认桌面环境,是一份中量级操作系统,并被设计为优雅而高效的桌面与如下特性的结合:配置简单、高…...

Nginx代理功能与负载均衡详解
序言 Nginx的代理功能与负载均衡功能是最常被用到的,关于nginx的基本语法常识与配置已在上篇文章中有说明,这篇就开门见山,先描述一些关于代理功能的配置,再说明负载均衡详细。 Nginx代理服务的配置说明 1、上一篇中我们在http…...
虚拟机常用命令)
部署问题集合(特辑)虚拟机常用命令
基础 查看ip:ip addr或ipconfig压缩:tar -zcvf redis-3.2.8.tar.gz redis-3.2.8/ 注意:-zcvf对应gz,-vcf对应tar 解压:tar -zxvf redis-3.2.8.tar.gz压缩zip:zip nginx.zip nginx.txt nginx2.txt解压zip&a…...

【Git】如何将本地文件进行Git仓库归档
Git 全局设置 git config --global user.name "mcihael" git config --global user.email "michael520.com"创建新版本库 git clone gitcode.xxxxxx.git cd branch-name touch README.md git add README.md git commit -m "add README" git pu…...

uniapp 使用腾讯视频 的 坑
1. 版本号的问题 注意 1.X.X不维护了 , 需要升级要 2.X.X 2. 官网的 组件事件 调用需要去掉bind 才能调用 官网地址:腾讯视频 | 小程序插件 | 微信公众平台...
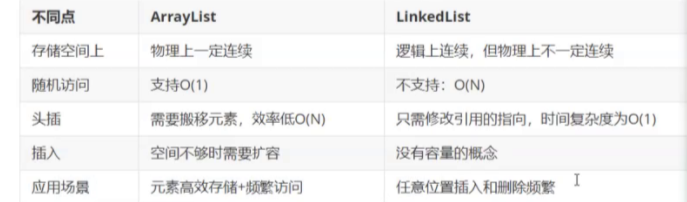
LinkedList
LinkedList的模拟实现(底层是一个双向链表)LinkedList使用 LinkedList的模拟实现(底层是一个双向链表) 无头双向链表:有两个指针;一个指向前一个节点的地址;一个指向后一个节点的地址。 节点定…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
