二叉搜索树的(查找、插入、删除)
一、二叉搜索树的概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
1、若它的左子树不为空,则左子树上所有节点的值都小于根节点的值;
2、若它的右子树不为空,则右子树上所有节点的值都大于根节点的值;
3、它的左右子树也分别为二叉搜索树
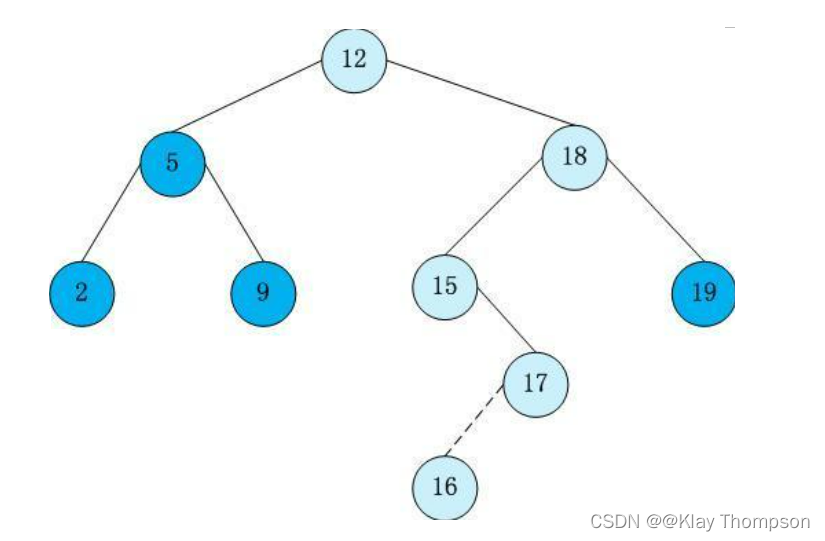
下图就是一个二叉搜索树:
二、二叉树的定义
template<class K>
struct BSTreeNode
{BSTreeNode<K>* _right;BSTreeNode<K>* _left;K _key;BSTreeNode(const K& key = K()):_right(nullptr),_left(nullptr),_key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool find(const K& key){}//查找bool insert(const K& key){}//插入 bool erase(const K& key){}//删除
private:Node* _root;
};三、二叉搜索树的查找节点
非递归写法:
如果root为空,那么查找失败,没有要查找的节点;如果root不为空,比较root->key和要查找的值,如果要查找的值大于root->key,就到右子树接着找,反之,到左子树接着找。找到返回true,没有找到返回false。
bool find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else{return true;}}return false;}递归写法:
查找思想还是和非递归一样的,如果root为空,返回false,如果root->key大于要找的值,那么递归到左子树去找(转换成一个子问题),反之,递归到右子树去找。
bool findR(const K& key){return _findR(_root, key);}bool _findR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key == key){return true;}else if(root->_key < key){return _findR(root->_right, key);}else{return _findR(root->_left, key);}}四、二叉搜索树的插入节点
非递归写法:
要插入一个数据,首先得找到插入的位置,所以插入分为两大步:
1、找到要插入的位置
如果树中存在一个节点的key与要插入的数相同,则不会插入。找位置的时候要同时有一个指针记录父节点,走到空就结束
2、插入数据
判断插入的数据比父节点大还是小,如果小则插在左边,反之则插在右边
bool insert(const K& key){if (_root == nullptr){_root = new Node(key);}else{Node* cur = _root;Node* parent = cur;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{return false;}}if (key > parent->_key){parent->_right = new Node(key);}else{parent->_left = new Node(key);}}return true;}递归写法:
bool insertR(const K& key){return _insertR(_root, key);}//这里要传引用,我们就不需要找父节点了bool _insertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _insertR(root->_right, key);}else if (root->_key > key){return _insertR(root->_left, key);}else{return false;}}五、二叉搜索树的删除节点
删除节点大致可分为三种情况:
1、要删除节点左右都为空;
2、要删除节点左为空或右为空;
3、要删除节点左右都不为空。
第一点和第二点又可以看成一点。
要注意特殊情况:要删除的节点是根节点。
非递归写法:
bool erase(const K& key){Node* cur = _root;Node* parent = cur;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}//找到要被删的节点了else{//1、要删除的这个节点是叶子节点或度为1(可直接删除)if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}else if(cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_right = cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}}//2、要删除的这个节点度为2(替换法)else{//找左树中的最大值或右树中的最小值与被删节点交换,再删除//找左树中的最大值Node* leftMax = cur->_left;Node* PLeftMax = cur;while (leftMax->_right){PLeftMax = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);//交换值//删除leftMaxif (PLeftMax->_right == leftMax){if (leftMax->_right == nullptr){PLeftMax->_right = leftMax->_left;}else{PLeftMax->_right = leftMax->_right;}}if (PLeftMax->_left == leftMax){if (leftMax->_right == nullptr){PLeftMax->_left = leftMax->_left;}else{PLeftMax->_left = leftMax->_right;}}cur = leftMax;}delete cur;return true;}}return false;}递归写法:
bool eraseR(const K& key){return _eraseR(_root, key);}bool _eraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _eraseR(root->_right, key);}else if (root->_key > key){return _eraseR(root->_left, key);}else{Node* del = root;//找到了被删除节点//1、左为空或右为空或左右都为空if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}//2、左右都不为空else{//左树找最大值Node* LeftMax = root->_left;while (LeftMax->_right){LeftMax = LeftMax->_right;}swap(root->_key, LeftMax->_key);//删除LeftMax节点return _eraseR(root->_left, key);}delete del;return true;}}六、二叉搜索树的应用
1、K模型(也就是我们后面学是set):K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
2、KV模型(也就是我们后面学是map):每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。
七、二叉搜索树的实现
template<class K>
struct BSTreeNode
{BSTreeNode<K>* _right;BSTreeNode<K>* _left;K _key;BSTreeNode(const K& key = K()):_right(nullptr),_left(nullptr),_key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& tree){_root = Copy(tree._root);}BSTree<K>& operator=(BSTree<K> tmp){swap(_root, tmp._root);return *this;}~BSTree(){Destory(_root);}bool insert(const K& key){if (_root == nullptr){_root = new Node(key);}else{Node* cur = _root;Node* parent = cur;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else{return false;}}if (key > parent->_key){parent->_right = new Node(key);}else{parent->_left = new Node(key);}}return true;}void InOrder(){_InOrder(_root);cout << endl;}bool find(const K& key){Node* cur = _root;while (cur){if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else{return true;}}return false;}bool erase(const K& key){Node* cur = _root;Node* parent = cur;while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}//找到要被删的节点了else{//1、要删除的这个节点是叶子节点或度为1(可直接删除)if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}else if(cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_right = cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}}//2、要删除的这个节点度为2(替换法)else{//找左树中的最大值或右树中的最小值与被删节点交换,再删除//找左树中的最大值Node* leftMax = cur->_left;Node* PLeftMax = cur;while (leftMax->_right){PLeftMax = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);//交换值//删除leftMaxif (PLeftMax->_right == leftMax){if (leftMax->_right == nullptr){PLeftMax->_right = leftMax->_left;}else{PLeftMax->_right = leftMax->_right;}}if (PLeftMax->_left == leftMax){if (leftMax->_right == nullptr){PLeftMax->_left = leftMax->_left;}else{PLeftMax->_left = leftMax->_right;}}cur = leftMax;}delete cur;return true;}}return false;}//-----------------------------------递归写法---------------------------------------bool findR(const K& key){return _findR(_root, key);}bool insertR(const K& key){return _insertR(_root, key);}bool eraseR(const K& key){return _eraseR(_root, key);}private:bool _eraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _eraseR(root->_right, key);}else if (root->_key > key){return _eraseR(root->_left, key);}else{Node* del = root;//找到了被删除节点//1、左为空或右为空或左右都为空if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}//2、左右都不为空else{//左树找最大值Node* LeftMax = root->_left;while (LeftMax->_right){LeftMax = LeftMax->_right;}swap(root->_key, LeftMax->_key);//删除LeftMax节点return _eraseR(root->_left, key);}delete del;return true;}}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* Croot = new Node(root->_key);Croot->_left = Copy(root->_left);Croot->_right = Copy(root->_right);return Croot;}void Destory(Node*& root){if (root == nullptr){return;}/*if (root->_left == nullptr && root->_right == nullptr){delete root;root = nullptr;return;}*/Destory(root->_left);Destory(root->_right);delete root;root = nullptr;}bool _insertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _insertR(root->_right, key);}else if (root->_key > key){return _insertR(root->_left, key);}else{return false;}}bool _findR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key == key){return true;}else if(root->_key < key){return _findR(root->_right, key);}else{return _findR(root->_left, key);}}void _InOrder(Node* root){//中序if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root;
};相关文章:
二叉搜索树的(查找、插入、删除)
一、二叉搜索树的概念 二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 1、若它的左子树不为空,则左子树上所有节点的值都小于根节点的值; 2、若它的右子树不为空,则右子树上所有节点的值都…...

电力虚拟仿真 | 高压电气试验VR教学系统
在科技进步的推动下,我们的教育方式也在发生着翻天覆地的变化。其中,虚拟现实(VR)技术的出现,为我们提供了一种全新的、富有沉浸感的学习和培训方式。特别是在电力行业领域,例如,电力系统的维护…...

innovus如何设置size only
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 给instance设置size only属性命令如下: dbset [dbGet top.inst.name aa/bb -p] .dontTouch sizeOk 给一个module设置size only需要foreach循环一下: foreach inst [dbGet top.…...

Java之继承详解二
3.7 方法重写 3.7.1 概念 方法重写 :子类中出现与父类一模一样的方法时(返回值类型,方法名和参数列表都相同),会出现覆盖效果,也称为重写或者复写。声明不变,重新实现。 3.7.2 使用场景与案例…...
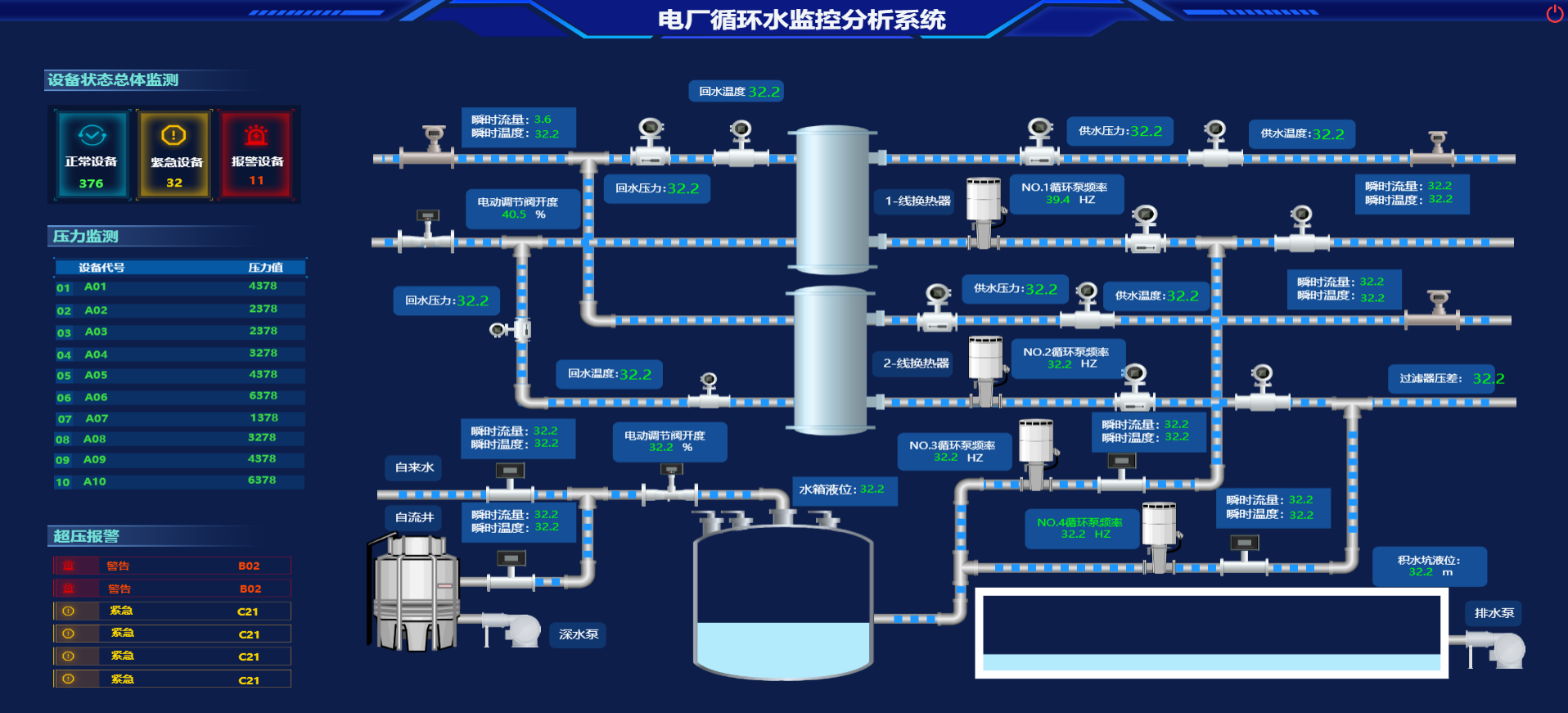
国内常见的几款可视化Web组态软件
组态软件是一种用于控制和监控各种设备的软件,也是指在自动控制系统监控层一级的软件平台和开发环境。这类软件实际上也是一种通过灵活的组态方式,为用户提供快速构建工业自动控制系统监控功能的、通用层次的软件工具。通常用于工业控制,自动…...
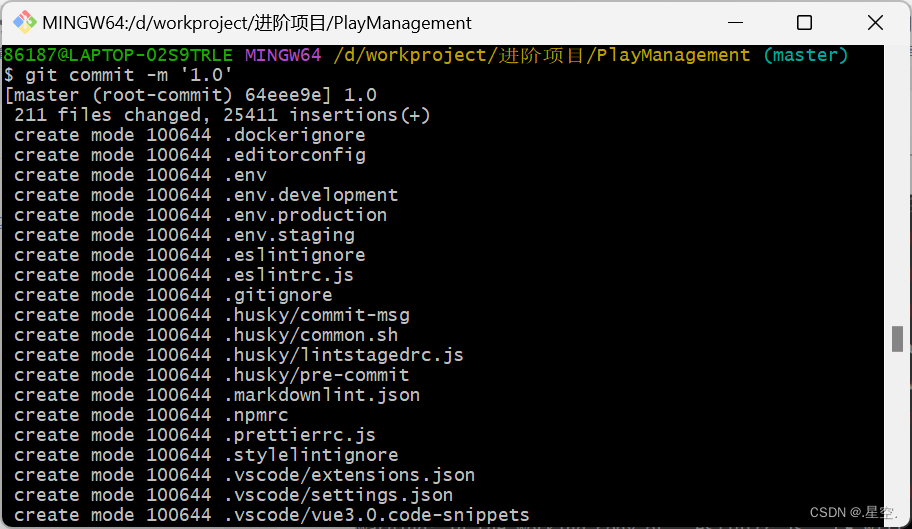
通过 git上传到 gitee 仓库
介绍 Git是目前世界上最先进的分布式版本控制系统,有这么几个特点: 分布式 :是用来保存工程源代码历史状态的命令行工具。保存点 :保存点可以追溯源码中的文件,并能得到某个时间点上的整个工程项目额状态;…...
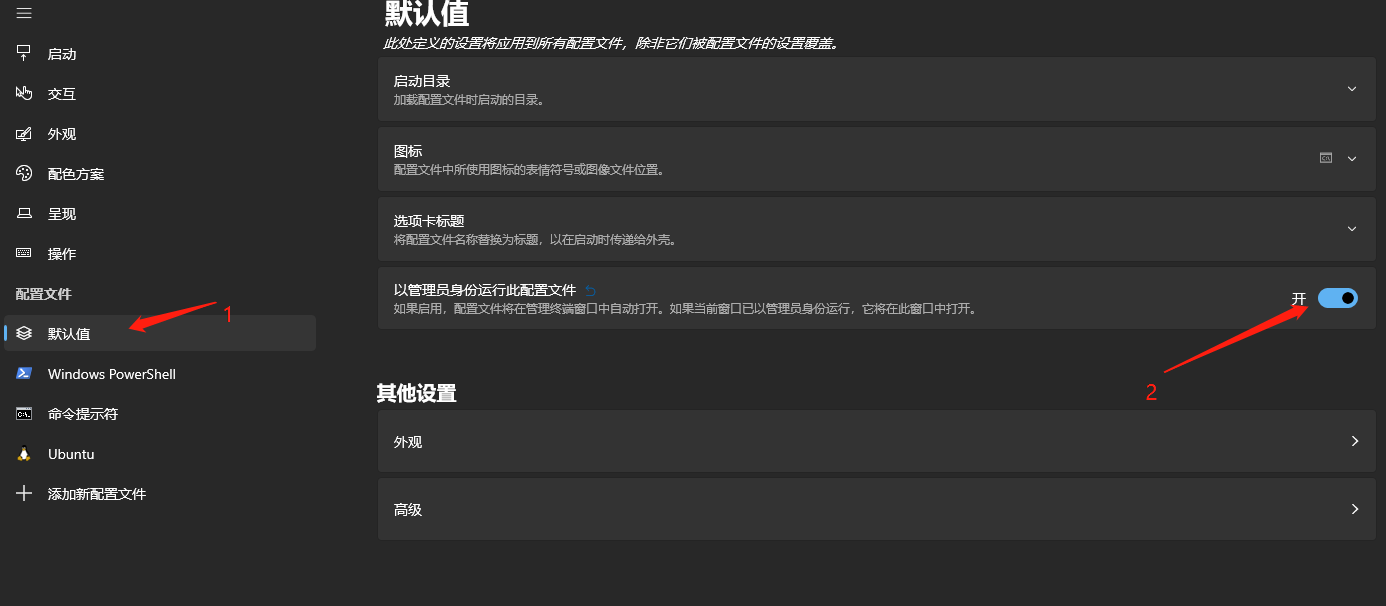
设置Windows主机的浏览器为wls2的默认浏览器
1. 准备工作 wsl是可以使用Windows主机上安装的exe程序,出于安全考虑,默认情况下改功能是无法使用。要使用的话,终端需要以管理员权限启动。 我这里以Windows Terminal为例,介绍如何默认使用管理员权限打开终端,具体…...
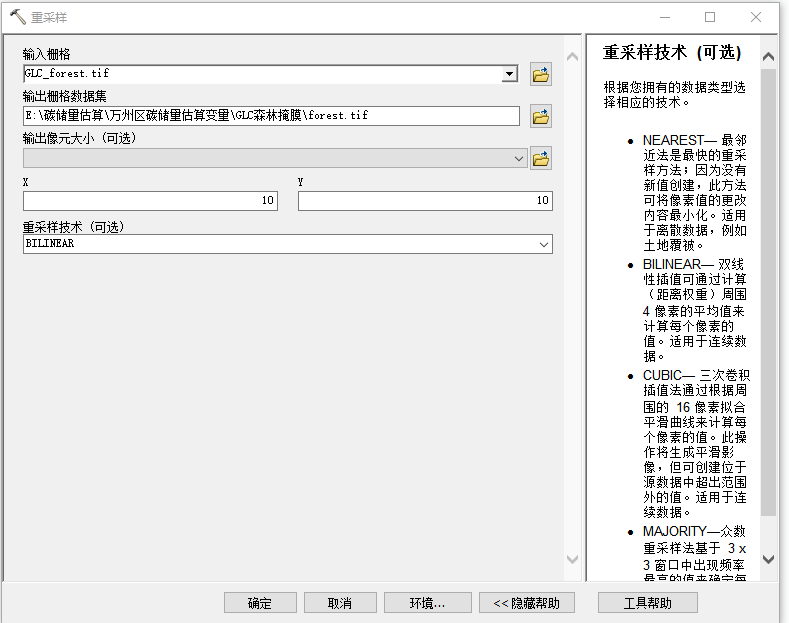
森林生物量(蓄积量)估算全流程
python森林生物量(蓄积量)估算全流程 一.哨兵2号获取/去云处理/提取参数1.1 影像处理与下载1.2 导入2A级产品1.3导入我们在第1步生成的云掩膜文件1.4.SNAP掩膜操作1.5采用gdal计算各类植被指数1.6 纹理特征参数提取 二.哨兵1号获取/处理/提取数据2.1 纹理…...
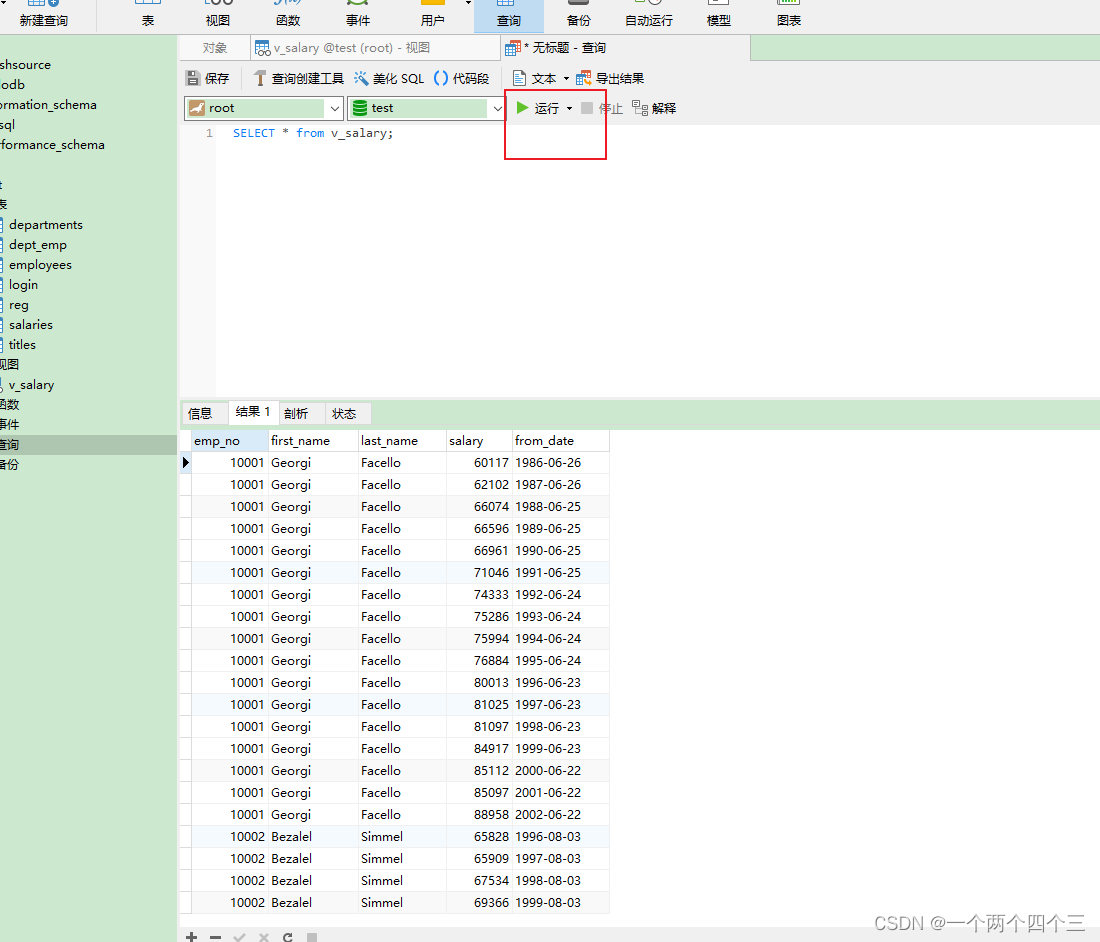
MySQL数据库概述
MySQL数据库概述 1 SQL SQL语句大小写不敏感。 SQL语句末尾应该使用分号结束。 1.1 SQL语句及相关操作示例 DDL:数据定义语言,负责数据库定义、数据库对象定义,由CREATE、ALTER与DROP三个语法所组成DML:数据操作语言ÿ…...

2023年国赛数学建模思路 - 案例:退火算法
文章目录 1 退火算法原理1.1 物理背景1.2 背后的数学模型 2 退火算法实现2.1 算法流程2.2算法实现 建模资料 ## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 退火算法原理 1.1 物理背景 在热力学上&a…...

怎么借助ChatGPT处理数据结构的问题
目录 使用ChatGPT进行数据格式化转换 代码示例 ChatGPT格式化数据提示语 代码示例 批量格式化数据提示语 代码示例 ChatGPT生成的格式化批处理代码 使用ChatGPT合并不同数据源的数据 合并数据提示语 自动合并数据提示语 ChatGPT生成的自动合并代码 结论 数据合并是…...
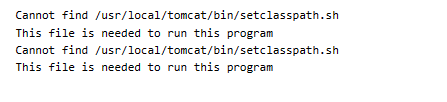
Docker容器无法启动 Cannot find /usr/local/tomcat/bin/setclasspath.sh
报错信息如下 解决办法 权限不够 加上--privileged 获取最大权限 docker run --privileged --name lenglianerqi -p 9266:8080 -v /opt/docker/lenglianerqi/webapps:/usr/local/tomcat/webapps/ -v /opt/docker/lenglianerqi/webapps/userfile:/usr/local/tomcat/webapps/u…...

Pytorch-day08-模型进阶训练技巧-checkpoint
PyTorch 模型进阶训练技巧 自定义损失函数动态调整学习率 典型案例:loss上下震荡 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BndMyRX0-1692613806232)(attachment:image-2.png)] 1、自定义损失函数 1、PyTorch已经提供了很多常用…...
:样式(Style)和符号(Symbol))
【ArcGIS Pro二次开发】(61):样式(Style)和符号(Symbol)
在 ArcGIS Pro SDK 中,地图要素符号(Symbol)和符号样式(Style)是2个很重要的概念。 【Symbol】是用于表示地图上不同类型的要素(如点、线、面)的图形化表示。 在地图中,各种要素都…...

深入理解 HTTP/2:提升 Web 性能的秘密
HTTP/2 是一项重大的网络协议升级,旨在提升 Web 页面加载速度和性能。在这篇博客中,我们将深入探讨 HTTP/2 的核心概念以及如何使用它来加速网站。 什么是 HTTP/2? HTTP/2 是 HTTP 协议的下一个版本,旨在解决 HTTP/1.1 中的性能…...
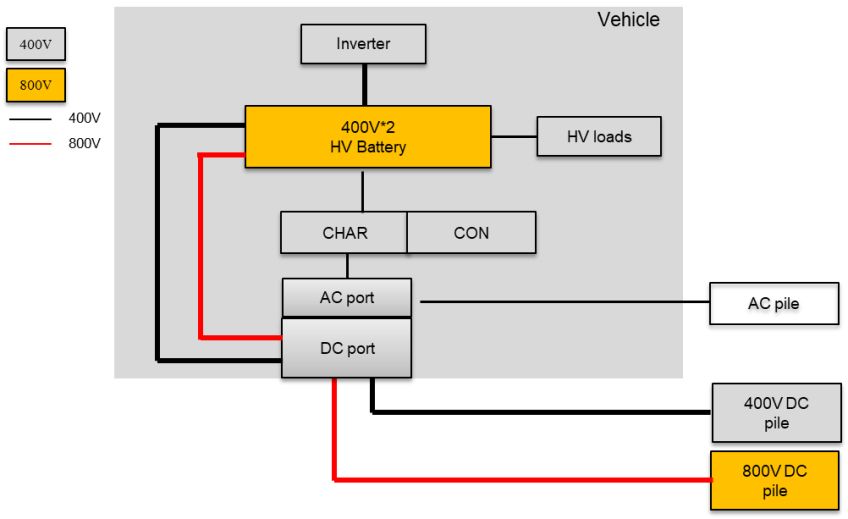
800V高压电驱动系统架构分析
需要电驱竞品样件请联:shbinzer (拆车邦) 过去一年是新能源汽车市场爆发的一年,据中汽协数据,2021年新能源汽车销售352万辆,同比大幅增长157.5%。新能源汽车技术发展迅速,畅销车辆在动力性能…...

Camunda_3:主动撤回
貌似国际主流认知工作流通常不支持撤回/驳回,流程只能向前进行。而撤回/驳回算是一种中国特色吧。 因此Camunda对于流程修改也仅仅提供了runtimeService.createProcessInstanceModification(instanceId)来修改流程。对于撤回/驳回这种操作得自己想办法。通常的撤回/…...

ClickHouse(二十三):Java Spark读写ClickHouse API
进入正文前,感谢宝子们订阅专题、点赞、评论、收藏!关注IT贫道,获取高质量博客内容! 🏡个人主页:含各种IT体系技术,IT贫道_Apache Doris,大数据OLAP体系技术栈,Kerberos安全认证-CSDN博客 &…...

Linux下的GPIO基本概念指南
一、什么是GPIO 在Linux中,GPIO(General Purpose Input/Output,通用输入输出)是一种用于控制外部设备和传感器的通用接口。它允许你通过软件控制数字信号,从而实现各种硬件设备的交互,如LED、按钮、传感器、马达等。 每个GPIO引脚…...

快速解决Spring Boot跨域困扰:使用CORS实现无缝跨域支持
跨域问题 什么是跨域? 跨域(Cross-Origin Issue)的存在是因为浏览器的安全限制,它防止恶意网站利用跨域请求来获取用户的敏感信息或执行恶意操作。浏览器通过实施同源策略来限制网页在不同源之间进行资源访问或交互的情况。当一…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
