2023年国赛数学建模思路 - 案例:退火算法
文章目录
- 1 退火算法原理
- 1.1 物理背景
- 1.2 背后的数学模型
- 2 退火算法实现
- 2.1 算法流程
- 2.2算法实现
- 建模资料
## 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 退火算法原理
1.1 物理背景
在热力学上,退火(annealing)现象指物体逐渐降温的物理现象,温度愈低,物体的能量状态会低;够低后,液体开始冷凝与结晶,在结晶状态时,系统的能量状态最低。大自然在缓慢降温(亦即,退火)时,可“找到”最低能量状态:结晶。但是,如果过程过急过快,快速降温(亦称「淬炼」,quenching)时,会导致不是最低能态的非晶形。
如下图所示,首先(左图)物体处于非晶体状态。我们将固体加温至充分高(中图),再让其徐徐冷却,也就退火(右图)。加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小(此时物体以晶体形态呈现)。
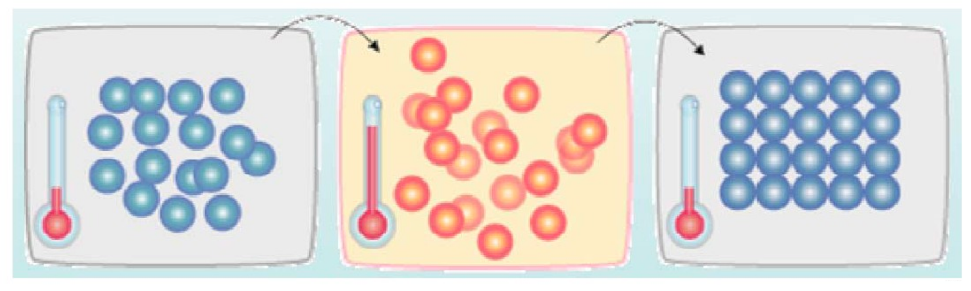
1.2 背后的数学模型
如果你对退火的物理意义还是晕晕的,没关系我们还有更为简单的理解方式。想象一下如果我们现在有下面这样一个函数,现在想求函数的(全局)最优解。如果采用Greedy策略,那么从A点开始试探,如果函数值继续减少,那么试探过程就会继续。而当到达点B时,显然我们的探求过程就结束了(因为无论朝哪个方向努力,结果只会越来越大)。最终我们只能找打一个局部最后解B。
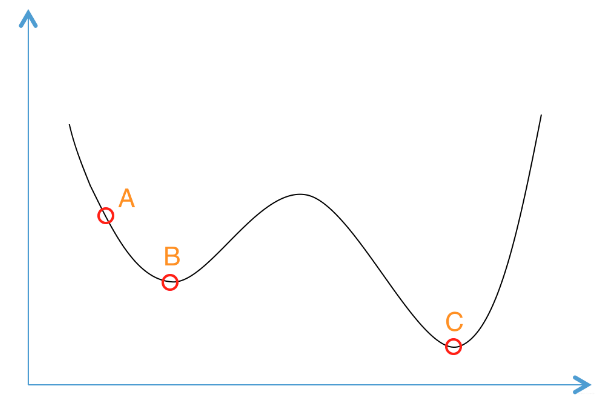
根据Metropolis准则,粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT)),其中E为温度T时的内能,ΔE为其改变数,k为Boltzmann常数。Metropolis准则常表示为
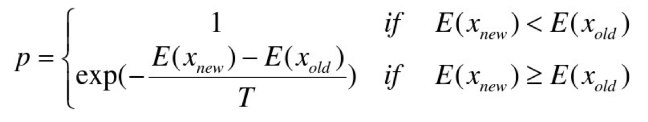
Metropolis准则表明,在温度为T时,出现能量差为dE的降温的概率为P(dE),表示为:P(dE) = exp( dE/(kT) )。其中k是一个常数,exp表示自然指数,且dE<0。所以P和T正相关。这条公式就表示:温度越高,出现一次能量差为dE的降温的概率就越大;温度越低,则出现降温的概率就越小。又由于dE总是小于0(因为退火的过程是温度逐渐下降的过程),因此dE/kT < 0 ,所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低,P(dE)会逐渐降低。
我们将一次向较差解的移动看做一次温度跳变过程,我们以概率P(dE)来接受这样的移动。也就是说,在用固体退火模拟组合优化问题,将内能E模拟为目标函数值 f,温度T演化成控制参数 t,即得到解组合优化问题的模拟退火演算法:由初始解 i 和控制参数初值 t 开始,对当前解重复“产生新解→计算目标函数差→接受或丢弃”的迭代,并逐步衰减 t 值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S。
2 退火算法实现
2.1 算法流程
(1) 初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点), 每个T值的迭代次数L
(2) 对k=1,……,L做第(3)至第6步:
(3) 产生新解S′
(4) 计算增量Δt′=C(S′)-C(S),其中C(S)为评价函数
(5) 若Δt′<0则接受S′作为新的当前解,否则以概率exp(-Δt′/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解,结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少,且T->0,然后转第2
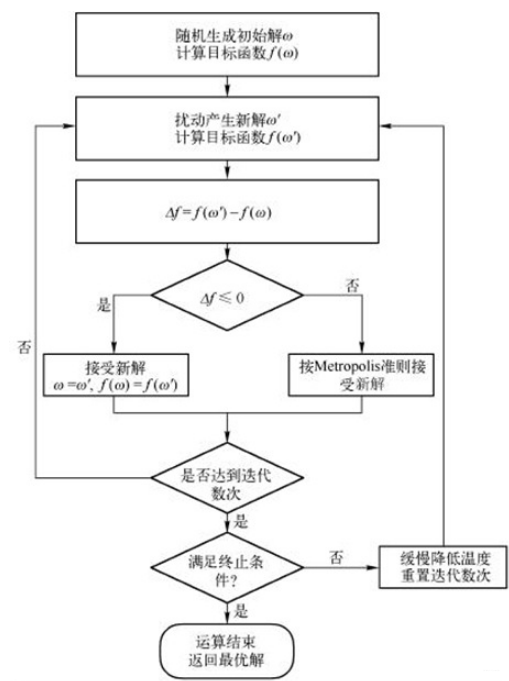
2.2算法实现
import numpy as np
import matplotlib.pyplot as plt
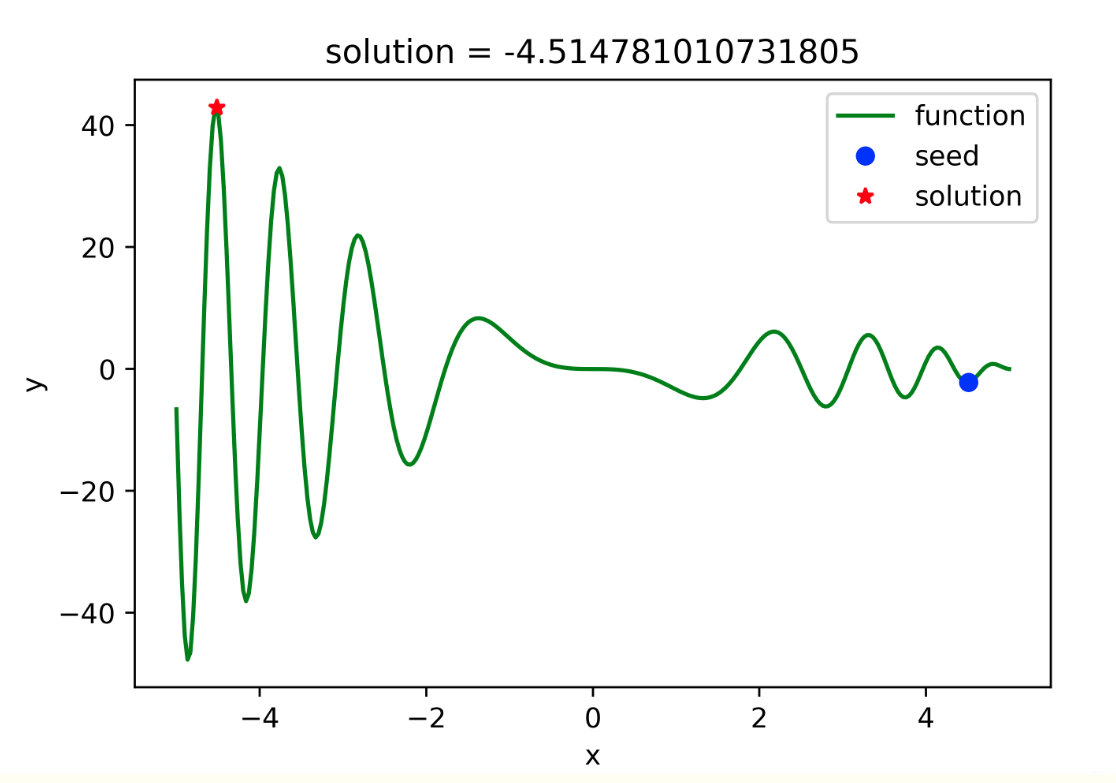
import randomclass SA(object):def __init__(self, interval, tab='min', T_max=10000, T_min=1, iterMax=1000, rate=0.95):self.interval = interval # 给定状态空间 - 即待求解空间self.T_max = T_max # 初始退火温度 - 温度上限self.T_min = T_min # 截止退火温度 - 温度下限self.iterMax = iterMax # 定温内部迭代次数self.rate = rate # 退火降温速度#############################################################self.x_seed = random.uniform(interval[0], interval[1]) # 解空间内的种子self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值#############################################################self.solve() # 完成主体的求解过程self.display() # 数据可视化展示def solve(self):temp = 'deal_' + self.tab # 采用反射方法提取对应的函数if hasattr(self, temp):deal = getattr(self, temp)else:exit('>>>tab标签传参有误:"min"|"max"<<<')x1 = self.x_seedT = self.T_maxwhile T >= self.T_min:for i in range(self.iterMax):f1 = self.func(x1)delta_x = random.random() * 2 - 1if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]: # 将随机解束缚在给定状态空间内x2 = x1 + delta_xelse:x2 = x1 - delta_xf2 = self.func(x2)delta_f = f2 - f1x1 = deal(x1, x2, delta_f, T)T *= self.rateself.x_solu = x1 # 提取最终退火解def func(self, x): # 状态产生函数 - 即待求解函数value = np.sin(x**2) * (x**2 - 5*x)return valuedef p_min(self, delta, T): # 计算最小值时,容忍解的状态迁移概率probability = np.exp(-delta/T)return probabilitydef p_max(self, delta, T):probability = np.exp(delta/T) # 计算最大值时,容忍解的状态迁移概率return probabilitydef deal_min(self, x1, x2, delta, T):if delta < 0: # 更优解return x2else: # 容忍解P = self.p_min(delta, T)if P > random.random(): return x2else: return x1def deal_max(self, x1, x2, delta, T):if delta > 0: # 更优解return x2else: # 容忍解P = self.p_max(delta, T)if P > random.random(): return x2else: return x1def display(self):print('seed: {}\nsolution: {}'.format(self.x_seed, self.x_solu))plt.figure(figsize=(6, 4))x = np.linspace(self.interval[0], self.interval[1], 300)y = self.func(x)plt.plot(x, y, 'g-', label='function')plt.plot(self.x_seed, self.func(self.x_seed), 'bo', label='seed')plt.plot(self.x_solu, self.func(self.x_solu), 'r*', label='solution')plt.title('solution = {}'.format(self.x_solu))plt.xlabel('x')plt.ylabel('y')plt.legend()plt.savefig('SA.png', dpi=500)plt.show()plt.close()if __name__ == '__main__':SA([-5, 5], 'max')
实现结果
建模资料
资料分享: 最强建模资料


相关文章:

2023年国赛数学建模思路 - 案例:退火算法
文章目录 1 退火算法原理1.1 物理背景1.2 背后的数学模型 2 退火算法实现2.1 算法流程2.2算法实现 建模资料 ## 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 退火算法原理 1.1 物理背景 在热力学上&a…...

怎么借助ChatGPT处理数据结构的问题
目录 使用ChatGPT进行数据格式化转换 代码示例 ChatGPT格式化数据提示语 代码示例 批量格式化数据提示语 代码示例 ChatGPT生成的格式化批处理代码 使用ChatGPT合并不同数据源的数据 合并数据提示语 自动合并数据提示语 ChatGPT生成的自动合并代码 结论 数据合并是…...
Docker容器无法启动 Cannot find /usr/local/tomcat/bin/setclasspath.sh
报错信息如下 解决办法 权限不够 加上--privileged 获取最大权限 docker run --privileged --name lenglianerqi -p 9266:8080 -v /opt/docker/lenglianerqi/webapps:/usr/local/tomcat/webapps/ -v /opt/docker/lenglianerqi/webapps/userfile:/usr/local/tomcat/webapps/u…...

Pytorch-day08-模型进阶训练技巧-checkpoint
PyTorch 模型进阶训练技巧 自定义损失函数动态调整学习率 典型案例:loss上下震荡 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BndMyRX0-1692613806232)(attachment:image-2.png)] 1、自定义损失函数 1、PyTorch已经提供了很多常用…...
:样式(Style)和符号(Symbol))
【ArcGIS Pro二次开发】(61):样式(Style)和符号(Symbol)
在 ArcGIS Pro SDK 中,地图要素符号(Symbol)和符号样式(Style)是2个很重要的概念。 【Symbol】是用于表示地图上不同类型的要素(如点、线、面)的图形化表示。 在地图中,各种要素都…...

深入理解 HTTP/2:提升 Web 性能的秘密
HTTP/2 是一项重大的网络协议升级,旨在提升 Web 页面加载速度和性能。在这篇博客中,我们将深入探讨 HTTP/2 的核心概念以及如何使用它来加速网站。 什么是 HTTP/2? HTTP/2 是 HTTP 协议的下一个版本,旨在解决 HTTP/1.1 中的性能…...
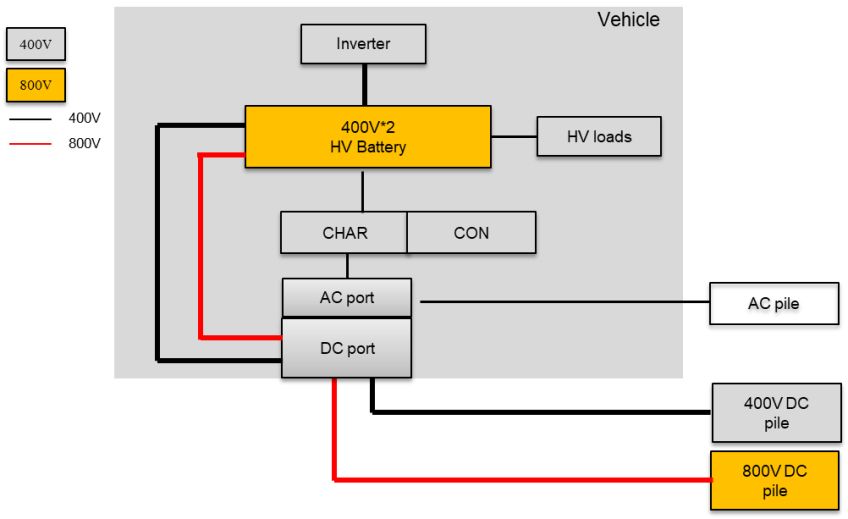
800V高压电驱动系统架构分析
需要电驱竞品样件请联:shbinzer (拆车邦) 过去一年是新能源汽车市场爆发的一年,据中汽协数据,2021年新能源汽车销售352万辆,同比大幅增长157.5%。新能源汽车技术发展迅速,畅销车辆在动力性能…...

Camunda_3:主动撤回
貌似国际主流认知工作流通常不支持撤回/驳回,流程只能向前进行。而撤回/驳回算是一种中国特色吧。 因此Camunda对于流程修改也仅仅提供了runtimeService.createProcessInstanceModification(instanceId)来修改流程。对于撤回/驳回这种操作得自己想办法。通常的撤回/…...

ClickHouse(二十三):Java Spark读写ClickHouse API
进入正文前,感谢宝子们订阅专题、点赞、评论、收藏!关注IT贫道,获取高质量博客内容! 🏡个人主页:含各种IT体系技术,IT贫道_Apache Doris,大数据OLAP体系技术栈,Kerberos安全认证-CSDN博客 &…...

Linux下的GPIO基本概念指南
一、什么是GPIO 在Linux中,GPIO(General Purpose Input/Output,通用输入输出)是一种用于控制外部设备和传感器的通用接口。它允许你通过软件控制数字信号,从而实现各种硬件设备的交互,如LED、按钮、传感器、马达等。 每个GPIO引脚…...

快速解决Spring Boot跨域困扰:使用CORS实现无缝跨域支持
跨域问题 什么是跨域? 跨域(Cross-Origin Issue)的存在是因为浏览器的安全限制,它防止恶意网站利用跨域请求来获取用户的敏感信息或执行恶意操作。浏览器通过实施同源策略来限制网页在不同源之间进行资源访问或交互的情况。当一…...

【【萌新的STM32学习-13之GPIO寄存器的用法】】
萌新的STM32学习-13之GPIO寄存器的用法 从外部来看我们有很多个GPIO 分为ABCDEF等等 每个GPIO都有16个引脚 每个引脚的名字是PA0到PA15 这是外部的看法 对于内部 引脚自然会有引脚的功能传入的模式 状态 频率 等…...

Android开发基础知识总结(一)初识安卓Android Studio
一.基础理论知识 1.Linux相当于是地基。 MIUI,EMUI等操作系统,是基于安卓的改版——且裁掉了一部分Google的服务。 (鸿蒙虽然是改版,但和安卓的架构基本上一致) 2.Kotlin和Java都是JVM语言,必须先复习好…...

常见的网络设备有哪些?分别有什么作用?
个人主页:insist--个人主页 本文专栏:网络基础——带你走进网络世界 本专栏会持续更新网络基础知识,希望大家多多支持,让我们一起探索这个神奇而广阔的网络世界。 目录 一、网络设备的概述 二、常见的网络设备 1、…...

斗鱼财报盈利的背后:左手艳舞、右手擦边
本月14日,直播平台斗鱼发布了其第二季度财报,面对“看起来还不错的数据”,其对外着重强调了“连续两个季度实现盈利”,并称“斗鱼收入结构持续优化”“斗鱼盈利能力提升”“斗鱼稳健增长可期”“督导提升了内容审核能力”。 财报…...
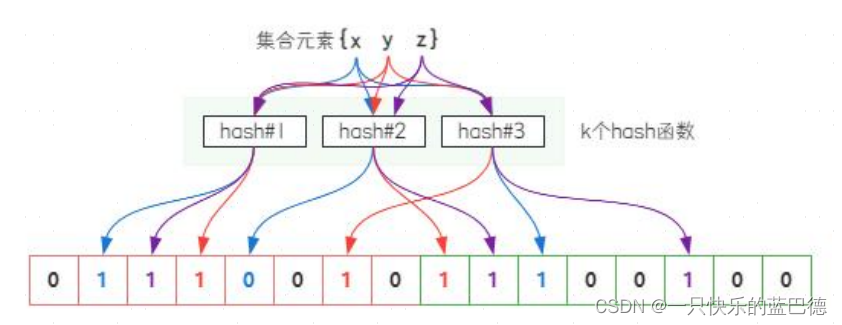
布隆过滤器
思考一个问题:如果我想判断一个元素是否存在某个集合里面怎么做? 一般的解决方案是先把所有元素保存起来,然后通过循环比较来确定。 但是如果我们有几千万甚至上亿的数据的时候},虽然可以通过不同的数据结构来优化数据…...
element-ui中二次封装一个带select的form组件
带select的form组件 样式 代码 <template><el-form-item label"是否有" class"append" prop"tag"><el-form-itemprop"isShare"><el-select v-model"query.tag"><el-option v-for"(item, …...

07.利用Redis实现点赞排行榜功能
学习目标: 提示:学习如何利用Redisson实现点赞排行榜功能,按照时间顺序 当用户给某一篇文章点赞后,会再数据库中存储一条数据,并且在Redis中存储一条数据为当前博客的点赞用户标识,来区分哪个用户对文章进…...

【前端vue升级】vue2+js+elementUI升级为vue3+ts+elementUI plus
一、工具的选择 近期想将vuejselementUI的项目升级为vue3tselementUI plus,以获得更好的开发体验,并且vue3也显著提高了性能,所以在此记录一下升级的过程对于一个正在使用的项目手工替换肯定不是个可实现的解决方案,更优方案是基于…...

多维时序 | MATLAB实现SCNGO-BiLSTM-Attention多变量时间序列预测
多维时序 | MATLAB实现SCNGO-BiLSTM-Attention多变量时间序列预测 目录 多维时序 | MATLAB实现SCNGO-BiLSTM-Attention多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 多维时序 | MATLAB实现SCNGO-BiLSTM-Attention多变量时间序列预测。 模型描…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
