并查集及其简单应用

文章目录
- 一.并查集
- 二.并查集的实现
- 三.并查集的基本应用
一.并查集
-
并查集的逻辑结构:由多颗不相连通的多叉树构成的森林(一个这样的多叉树就是森林的一个连通分量)
- 并查集的元素(树节点)用
0~9的整数表示,并查集可以表示如下: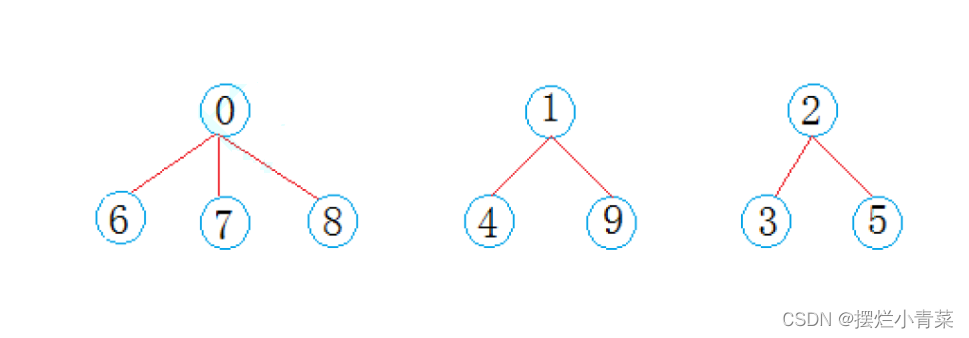
- 并查集的元素(树节点)用
-
并查集的物理存储结构:并查集一般采用顺序结构实现,用数组下标表示并查集的元素,数组元素用于记录并查集中的元素间的关系:
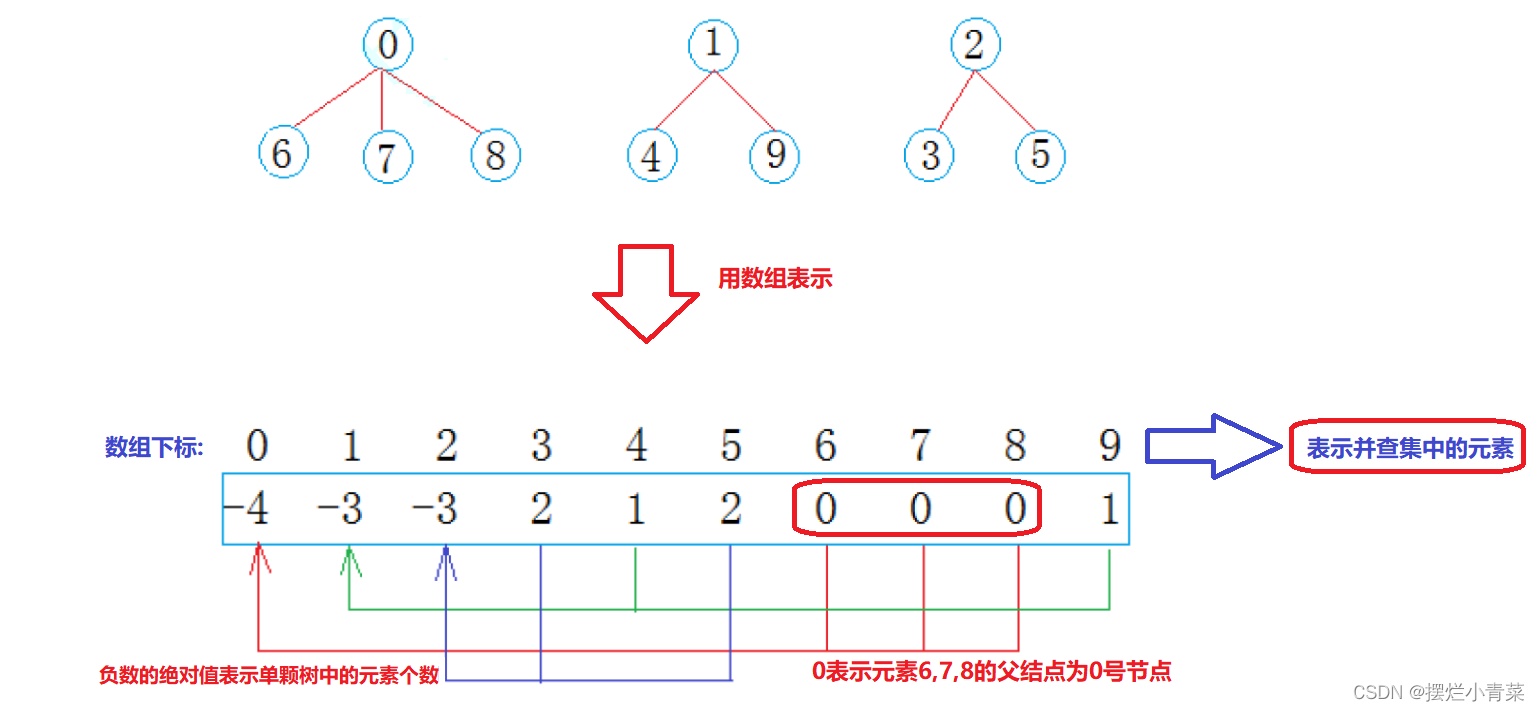
- 若并查集的元素对应的数组元素为负数,则表示该并查集元素为某颗多叉树的根且没有前驱结点,负数的绝对值表示该颗多叉树(并查集的连通分量)的元素个数
- 若并查集的元素对应的数组元素为非负数,这个非负数则表示该并查集的元素的前驱结点
-
并查集数据结构常用的运算就是==(连通分量)多叉树间的合并算法==:
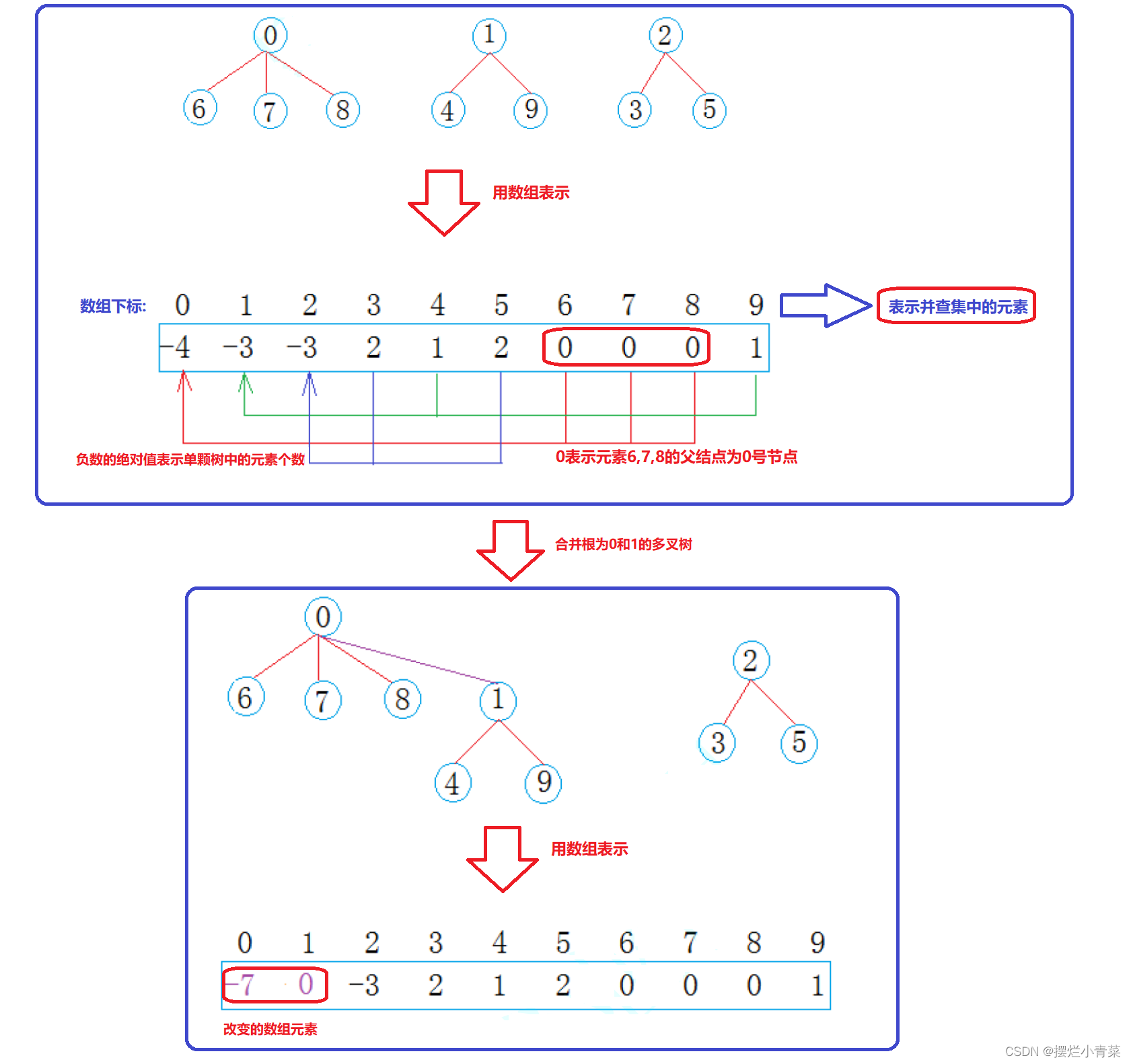
二.并查集的实现
- 并查集的初始状态设置:

- 简单的代码实现:
#include <iostream>
#include <vector>
#include <string>//采用适配器模式实现并查
class UnionFindSet
{
public://构造函数参数为并查集中的元素个数,并查集的初始状态为size颗树构成的森林(size个连通分量)UnionFindSet(size_t size):_SetMap(size,-1){}//给定一个并查集元素找到其所在的(连通分量)多叉树的根结点size_t FindRoot(int Node) const throw(std :: string){//越界检查if (Node < 0 || Node >= _SetMap.size())throw "Label out of range"; while (_SetMap[Node] >= 0){Node = _SetMap[Node];}return static_cast<size_t>(Node);}//给定两个并查集元素,将它们所在的(连通分量)多叉树进行合并运算void Union(int Node1, int Node2) throw(std::string){//越界检查if (Node1 < 0 || Node1 > _SetMap.size()|| Node2 < 0 || Node2 > _SetMap.size())throw "Label out of range";//先找到两个元素所在的(连通分量)多叉树的根size_t root1 = FindRoot(Node1);size_t root2 = FindRoot(Node2);//进行多叉树合并操作if (root1 != root2){_SetMap[root1] += _SetMap[root2];_SetMap[root2] = static_cast<int>(root1);}}//计算并查集中多叉树的颗数(连通分量的个数)size_t SetCount() const noexcept{//并查集中多叉树的颗数就是vector中负数元素的个数size_t count = 0;for (auto e : _SetMap){if (e < 0)++count;}return count;}
private:std::vector<int> _SetMap;
};
- 并查集是一种经常用于划分等价类的数据结构.以树形逻辑结构为基础,以一颗多叉树(一个连通分量)表示一个等价类,多个互相不连通的多叉树(连通分量)构成的森林用于表示多个等价类构成的集合,使用并查集可以很好地解决等价类的划分和计数问题(即图的连通分量的求解问题)
三.并查集的基本应用
LeetCoed : LCR 116. 省份数量
- 这个问题就是一个等价类集合的构建和计数问题,可以使用并查集解决.(题目中的相连关系就是一种相对于相同省份性质的等价关系)
- 问题的本质可以抽象为:以城市为元素依据相连关系形成的图结构的最小生成树的个数(即连通分量的个数),可以采用
dfs或bfs遍历算法,此处提供使用并查集的一种写法. - 借助
vector和lambda表达式建立简单的并查集最后返回并查集中多叉树的个数:
class Solution
{
public:int findCircleNum(vector<vector<int>>& isConnected) {//创建简易的并查集vector<int> UnionSet(isConnected.size(),-1);//定义Find函数,根据结点找到多叉树的根auto Find = [&UnionSet](int Node){while(UnionSet[Node] >=0){Node = UnionSet[Node];}return Node;};for(int i = 0; i < isConnected.size(); ++i){for(int j = i+1; j < isConnected.size(); ++j){if(isConnected[i][j] == 1){//多叉树合并int root1 = Find(i);int root2 = Find(j);if(root1 != root2){UnionSet[root1] += UnionSet[root2];//这句代码用于修改结点计数,此题中可以不加UnionSet[root2] = root1;}}}}int count = 0;//统计并查集中多叉树的个数for(auto e : UnionSet){if(e < 0 ) ++count;}return count;}
};
LeetCode:990. 等式方程的可满足性
- 这同样是一个等价类划分的问题:将
0~25的各个编号与a~z二十六个字母建立映射关系,根据字母间相等关系构建并查集:
class Solution
{
public:bool equationsPossible(vector<string>& equations) {vector<int> UionSet(26,-1);auto FindRoot = [&UionSet](int Node){while(UionSet[Node] >= 0){Node = UionSet[Node];}return Node;};//先遍历等式方程中的字母,在并查集中将它们归类到各个多叉树中(构建相等关系等价类集合)for(auto str : equations){//遇到等式,等式两边字母应该属于并查集中同一颗多叉树if(str[1] == '='){int root1 = FindRoot(str[0]-'a');int root2 = FindRoot(str[3]-'a');if(root1 != root2){UionSet[root1] += UionSet[root2];UionSet[root2] = root1;}}}//再处理不等式方程,检验相容性for(auto str : equations){//遇到不等式,不等式两边字母不能属于并查集中同一颗多叉树if(str[1] == '!'){int root1 = FindRoot(str[0]-'a');int root2 = FindRoot(str[3]-'a');if(root1 == root2){return false;}}}return true;}
};

相关文章:

并查集及其简单应用
文章目录 一.并查集二.并查集的实现三.并查集的基本应用 一.并查集 并查集的逻辑结构:由多颗不相连通的多叉树构成的森林(一个这样的多叉树就是森林的一个连通分量) 并查集的元素(树节点)用0~9的整数表示,并查集可以表示如下: 并查集的物理存储结构:并查集一般采用顺序结构实…...
基于web的服装商城系统java网上购物商店jsp源代码mysql
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 基于web的服装商城系统 系统有1权限:前台…...

.NET Core发布到IIS
项目介绍 1、开发工具Visual Studio 2017,语言C#,SQL SERVER,WIN10 2、本地IIS,手机上或其他用户在和本地在同一个局域网内访问,同时要把防火墙关掉 3、IIS全名Internet Information Services,用来发布网站 先决条件 安…...
Spring的基本概念
前言 Spring 究竟是什么?其实Spring简单来说就是一个包含众多工具方法的IOC容器。 那么什么是IOC呢? IoC Inversion of Control 翻译成中⽂是“控制反转”的意思. 既然Spring 是⼀个IoC(控制反转)容器,重点还在“容…...

设计模式之原型模式
文章目录 一、介绍二、实现步骤三、案例四、应用五、细胞分裂六、改造细胞分裂逻辑七、总结 一、介绍 原型模式属于创建型设计模式,用于创建重复的对象,且同时又保证了性能。 该设计模式的好处是将对象的创建与调用方分离。 其目的就是**根据一个对象…...

正则表达式在网页处理中的应用四则
正则表达式在网页处理中的应用四则 正则表达式(Regular Expression)为字符串模式匹配提供了一种高效、方便的方法。几乎所有高级语言都提供了对正则表达式的支持,或者提供了现成的代码库供调用。本文以ASP环境中常见的处理任务为例,介绍正则表达式的应用技巧。 一、检验密…...

ping使用方法
文章目录 1、Ping的基础知识2、Ping命令详解3、怎样使用Ping这命令来测试网络连通?4、如何用Ping命令来判断一条链路好坏?5、对Ping后返回信息的分析1.Request timed out2.Destination host Unreachable 1、Ping的基础知识 ping命令相信大家已经再熟悉不…...

“心理健康人工智能产学研创新联盟”揭牌成立|深兰科技
8月14日上午,“2023树洞救援年会”在上海举行,会上举行了“心理健康人工智能产学研创新联盟”的签约和揭牌仪式。“树洞行动救援团”创始人深兰科技科学院智能科学首席科学家、荷兰阿姆斯特丹自由大学人工智能系终身教授黄智生,深兰科技集团创…...
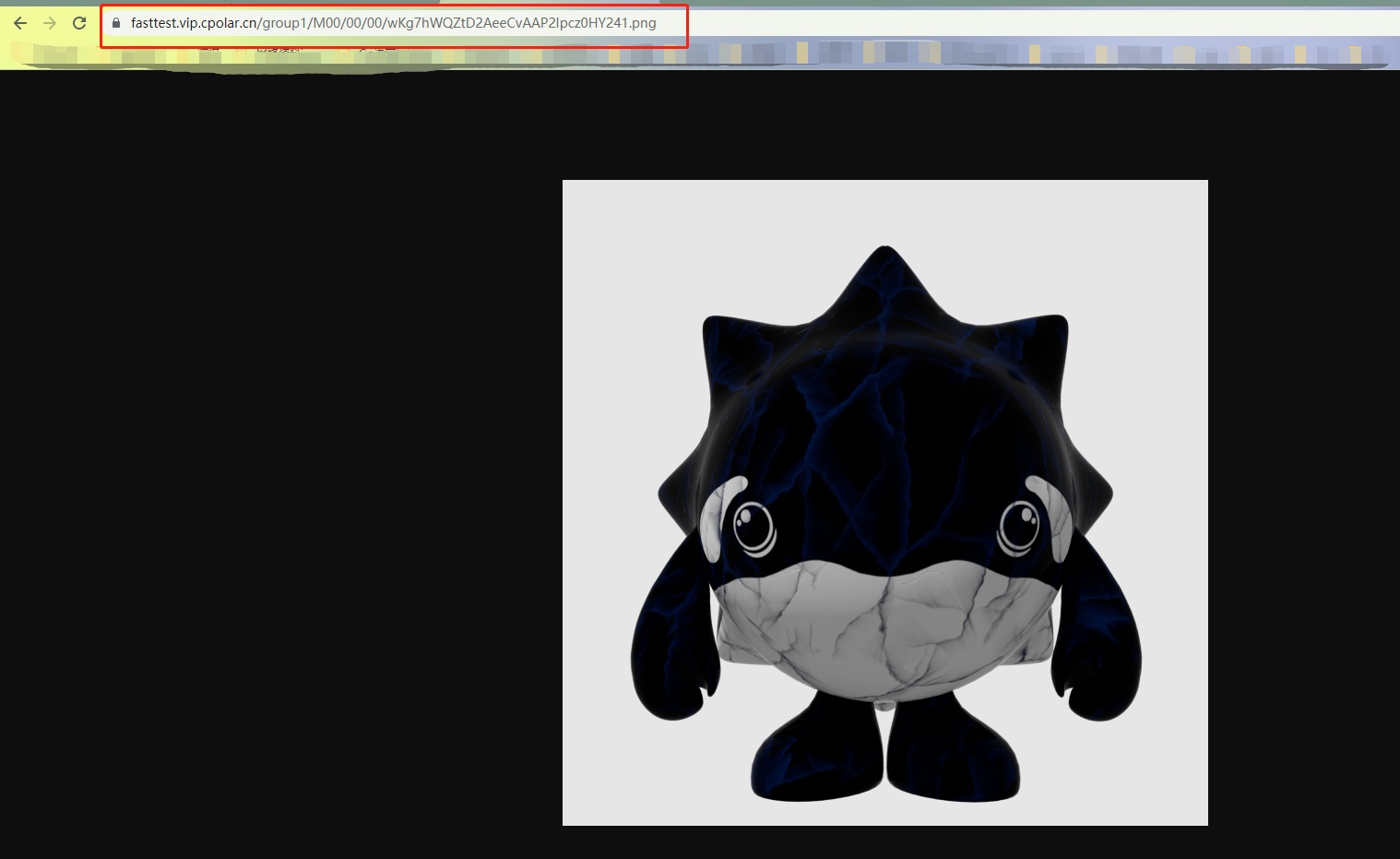
FastDFS+Nginx - 本地搭建文件服务器同时实现在外远程访问「端口映射」
文章目录 前言1. 本地搭建FastDFS文件系统1.1 环境安装1.2 安装libfastcommon1.3 安装FastDFS1.4 配置Tracker1.5 配置Storage1.6 测试上传下载1.7 与Nginx整合1.8 安装Nginx1.9 配置Nginx 2. 局域网测试访问FastDFS3. 安装cpolar内网穿透4. 配置公网访问地址5. 固定公网地址5.…...
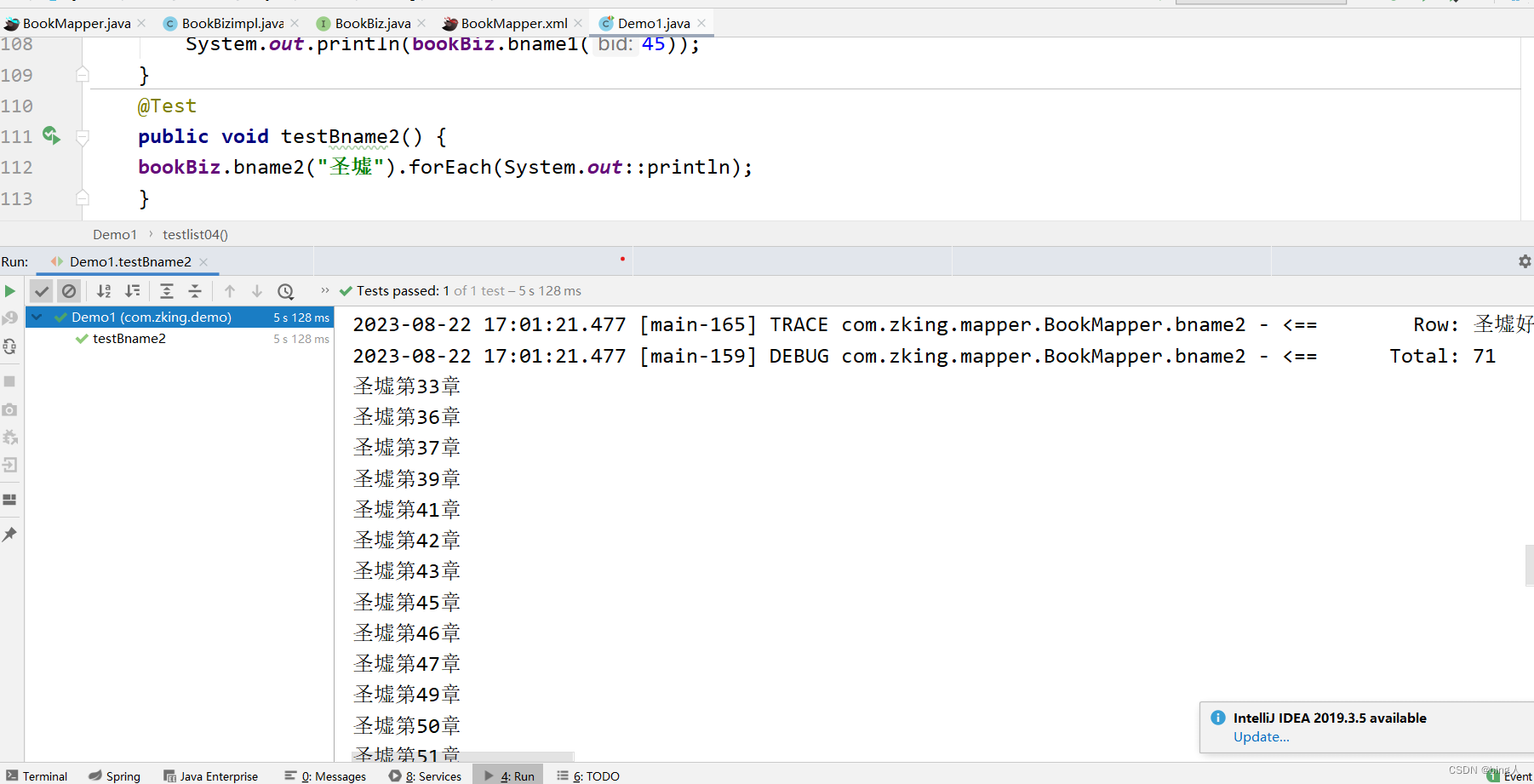
Mybatis-动态sql和分页
目录 一.什么是Mybatis动态分页 二.mybatis中的动态SQL 在BookMaaper.xml中写sql BookMapper BookBiz接口类 BookBizImpl实现接口类 demo测试类 编辑 测试结果 三.mybatis中的模糊查询 mybatis中的#与$有是什么区别 在BookMapper.xml里面建立三个模糊查询 编辑 …...

基于YOLOV8模型的西红柿目标检测系统(PyTorch+Pyside6+YOLOv8模型)
摘要:基于YOLOV8模型的西红柿目标检测系统可用于日常生活中检测与定位西红柿目标,利用深度学习算法可实现图片、视频、摄像头等方式的目标检测,另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检测算法训练数…...
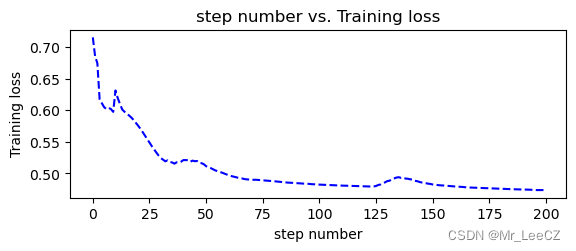
数学建模及数据分析 || 4. 深度学习应用案例分享
PyTorch 深度学习全连接网络分类 文章目录 PyTorch 深度学习全连接网络分类1. 非线性二分类2. 泰坦尼克号数据分类2.1 数据的准备工作2.2 全连接网络的搭建2.3 结果的可视化 1. 非线性二分类 import sklearn.datasets #数据集 import numpy as np import matplotlib.pyplot as…...

数据分析15——office中的Excel基础技术汇总
0、前言: 这部分总结就是总结每个基础技术的定义,在了解基础技术名称和定义后,方便对相关技术进行检索学习。笔记不会详细到所有操作都说明,但会把基础操作的名称及作用说明,可自行检索。本文对于大部分读者有以下作用…...
C语言好题解析(四)
目录 选择题一选择题二选择题三选择题四选择题五编程题一 选择题一 已知函数的原型是: int fun(char b[10], int *a); 设定义: char c[10];int d; ,正确的调用语句是( ) A: fun(c,&d); B: fun(c,d); C: fun(&…...

英语——主谓一致
主谓一致是指句子的谓语动词与其主语在数上必须保持一致,一般遵循以下三个原则: 一、语法形式上一致,即单复数形式与谓语要一致。 二、意义上一致,即主语意义上的单复数要与谓语的单复数形式一致。 三、就近以及就远原则,即谓语动词的单复形式取决于最靠近它的词语或者离它…...

属性字符串解析
连续的KV的字符串,每个KV之间用","分隔,V中可嵌套KV的连续字符串结构,例如“ key1value1,key2value2,key3[key4value4,key5value5,key6[key7value7]],key8value8 请编写如下函数,给定字符串,输出嵌套结构的H…...
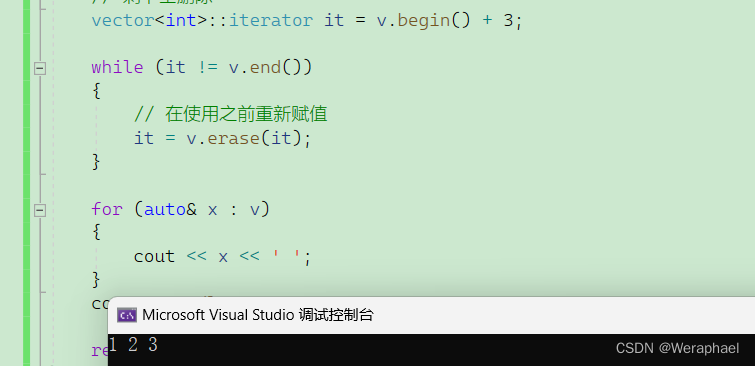
【C++初阶】vector容器
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:C航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞…...

ThreadLocal深度解析
简介 在并发编程中,导致并发bug的问题都会归结于对共享变量的操作不当。多个线程同时读写同一共享变量存在并发问题,我们可以利用写时复制、不变性来突破对原数据的写操作,没有写就没有并发问题,而本篇文章所介绍的技术是突破共享…...

06有监督学习——迁移学习
1.迁移学习分类 (1) 基于实例的迁移学习方法: 假设:源域中的一些数据和目标域会共享很多共同的特征方法:对源域进行instance reweighting,筛选出与目标域数据相似度高的数据,然后进行训练学习 (2&#x…...

快速连接服务器脚本 可从多个服务中选择并连接
使用 python 做一个可选择服务器登录连接的脚本 前置条件 需要有python 环境python --version 显示版本号即可检查 python 是否有 paramiko 包没有的话 python install paramiko创建一个python 文件,内容如下 # -*- coding: utf-8 -*-""" Authors: huxiaohua…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
