解决npm安装依赖失败,node和node-sass版本不匹配的问题
npm安装依赖报错: npm ERR! cb() never called! npm ERR! This is an error with npm itself.
一. 问题描述
用npm安装依赖报错:
npm ERR! cb() never called!
npm ERR! This is an error with npm itself. Please report this error at:
npm ERR! <https://npm.community>
npm ERR! A complete log of this run can be found in:
npm ERR! C:\Users\Administrator\AppData\Roaming\npm-cache\_logs\2020-12-16T07_38_47_793Z-debug.log
二. 问题解决
这个问题困扰了大半天,网上答案五花八门,不过对我来说,那些方法都没有效果,记录一下我解决这个错误的步骤,如下:
- 删除下载好的node_modules
- 删除package-lock.json文件
- 清除npm缓存 npm cache clean --force 或者是 npm cache verify
- npm install
三. 注意事项
另外,使用这个方法的前提条件就是你的npm源可连接并且有权限获取到里代码里使用的包,
并且解决了之前的报错问题,如果没有有权限,请修改包版本或者修改npm源。
1. 修改包版本
node-sass对应的node版本的包可以看下面这个表

我的项目node-sass版本是4.9.0 ,安装node高版本的不行,就降级14.17.3 也可以是别的版本
node历史版本地址:
CNPM Binaries Mirror![]() https://registry.npmmirror.com/binary.html?path=node/
https://registry.npmmirror.com/binary.html?path=node/
2.查看npm源为淘宝源或者可以用的其他源
//查看源
npm config get registry
//更换源
npm config set registry https://registry.npmjs.org
//淘宝源
npm config set registry https://registry.npm.taobao.org
3.如果还报错那么可以用npm config ls 查看有没有.npmc这个文件
.npmrc,可以理解成npm running cnfiguration, 即npm运行时配置文件。简单点说, .npmrc 可以设置 package.json 中依赖包的安装来源,既从哪里下载依赖包。
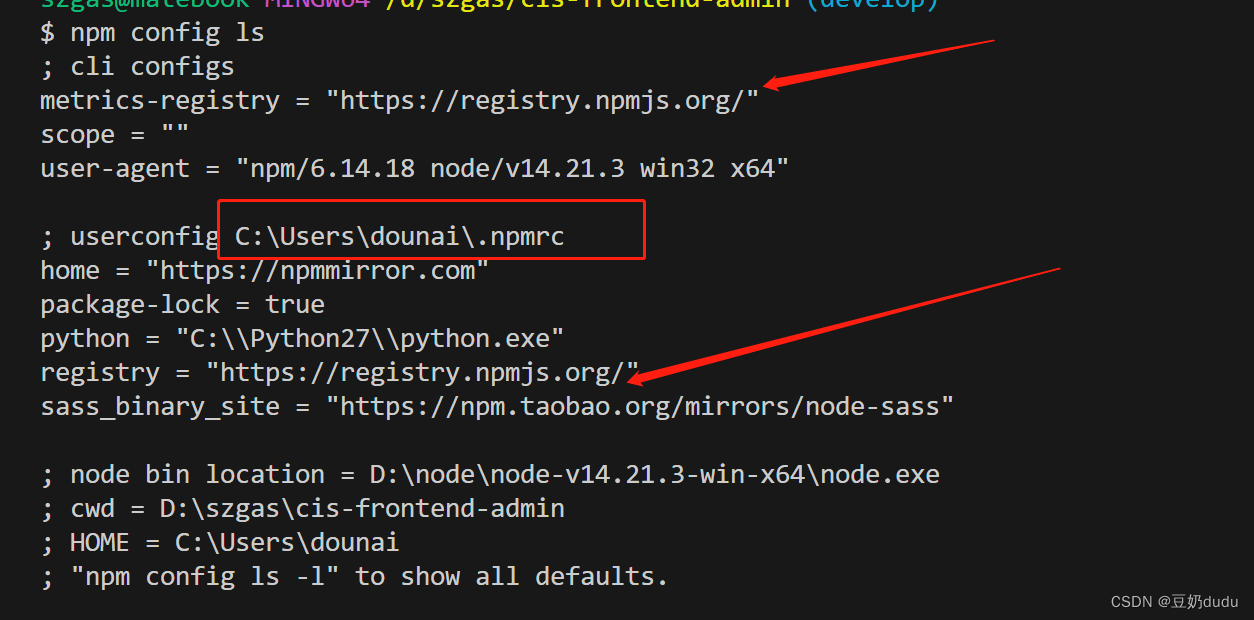
我的问题是用户下面的.npmc这个文件的淘宝源是旧版的registry.npm.taobao.org
上面那张图是更改后的的,之前是registry = "https://registry.npm.taobao.org"
这个是旧的淘宝源域名了, 现在更新了新域名, 所以一些依赖就会出现问题
域名切换:
-
npm.taobao.org => npmmirror.com
-
registry.npm.taobao.org => registry.npmmirror.com
.npmc安装的优先级
电脑中有多个 .npmrc 文件,在我们安装包的时候,npm按照如下顺序读取这些配置文件
项目配置文件: /project/.npmrc
用户配置文件:~/.npmrc
全局配置文件:$PREFIX/etc/npmrc
npm 内置配置文件 /path/to/npm/npmrc
我受影响的就是用户配置文件.npmrc
实在不知道怎么配置用户文件, 可以删除用户配置文件, 就不会受干扰的
问题解决参考:
【已解决】npm安装依赖报错: npm ERR! cb() never called! npm ERR! This is an error with npm itself._https://npm.community_清宵尚温。的博客-CSDN博客
一直报错npm ERR! cb() never called!删除缓存仍然不行 - 掘金 (juejin.cn)
相关文章:

解决npm安装依赖失败,node和node-sass版本不匹配的问题
npm安装依赖报错: npm ERR! cb() never called! npm ERR! This is an error with npm itself. 一. 问题描述 用npm安装依赖报错: npm ERR! cb() never called! npm ERR! This is an error with npm itself. Please report this error at: npm ERR! …...
2023 网络建设与运维 X86架构计算机操作系统安装与管理题解
任务描述: 随着信息技术的快速发展,集团计划2023年把部分业务由原有的X86架构服务器上迁移到ARM架构服务器上,同时根据目前的部分业务需求进行了部分调整和优化。 一、X86架构计算机操作系统安装与管理 1.PC1系统为ubuntu-desktop-amd64系统(已安装,语言为英文),登录用户…...
LAMP 架构及Discuz论坛与Wordpress博客搭建
目录 1 LAMP 配置与应用 1.1动态资源与语言 1.2 LAMP 架构的组成 1.2.1 主要功能 2 编译安装Apache http 服务 2.1 环境准备 2.1.1 关闭防火墙及selinux服务 2.1.2 安装依赖环境 2.2 安装软件包 2.2.1 解压软件包 2.2.2 移动apr包 apr-util包到安装目录中,并…...

考研C语言进阶题库——更新51-60题
目录 51.银行系中有很多恒星,H 君晚上无聊,便爬上房顶数星星,H 君将整个银河系看做一个平面,左上角为原点(坐标为(1, 1))。现在有 n 颗星星,他给每颗星星都标上坐标&…...

智能算法挑战赛决赛题目——初中组
题目 1. 判断是否存在重复的子序列 从 m 个字符中选取字符,生成 n 个符号的序列,使得其中没有 2 个相邻的子序列相同。如从 1,2,3,生成长度为 5 的序列,序列“12321”是合格的,而“12323”和“…...
一分钟学算法-递归-斐波那契数列递归解法及优化
一分钟学一个算法题目。 今天我们要学习的是用递归算法求解斐波那契数列。 首先我们要知道什么是斐波那契数列。 斐波那契数列,又称黄金分割数列,是一个经典的数学数列,其特点是第一项,第二项为1,后面每个数字都是前…...

选择Rust,并在Ubuntu上使用Rust
在过去的 8 年里,Rust 一直是开发人员最喜欢的语言,并且越来越被各种规模的软件公司采用。然而,它的许多高级规则和抽象创造了一个陡峭的初始学习曲线,这可能会给人留下 Rust 是少数人的保留的印象,但这与事实相去甚远…...

SVM详解
公式太多了,就用图片用笔记呈现,SVM虽然算法本质一目了然,但其中用到的数学推导还是挺多的,其中拉格朗日约束关于α>0这块证明我看了很长时间,到底是因为悟性不够。对偶问题也是,用了一个简单的例子才明…...
mysql全文检索使用
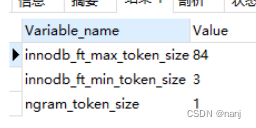
数据库数据量10万左右,使用like %test%要耗费30秒左右,放弃该办法 使用mysql的全文检索 第一步:建立索引 首先修改一下设置: my.ini中ngram_token_size 1 可以通过 show variables like %token%;来查看 接下来建立索引:alter table 表名 add f…...

opencv 进阶17-使用K最近邻和比率检验过滤匹配(图像匹配)
K最近邻(K-Nearest Neighbors,简称KNN)和比率检验(Ratio Test)是在计算机视觉中用于特征匹配的常见技术。它们通常与特征描述子(例如SIFT、SURF、ORB等)一起使用,以在图像中找到相似…...
Mac Flutter web环境搭建
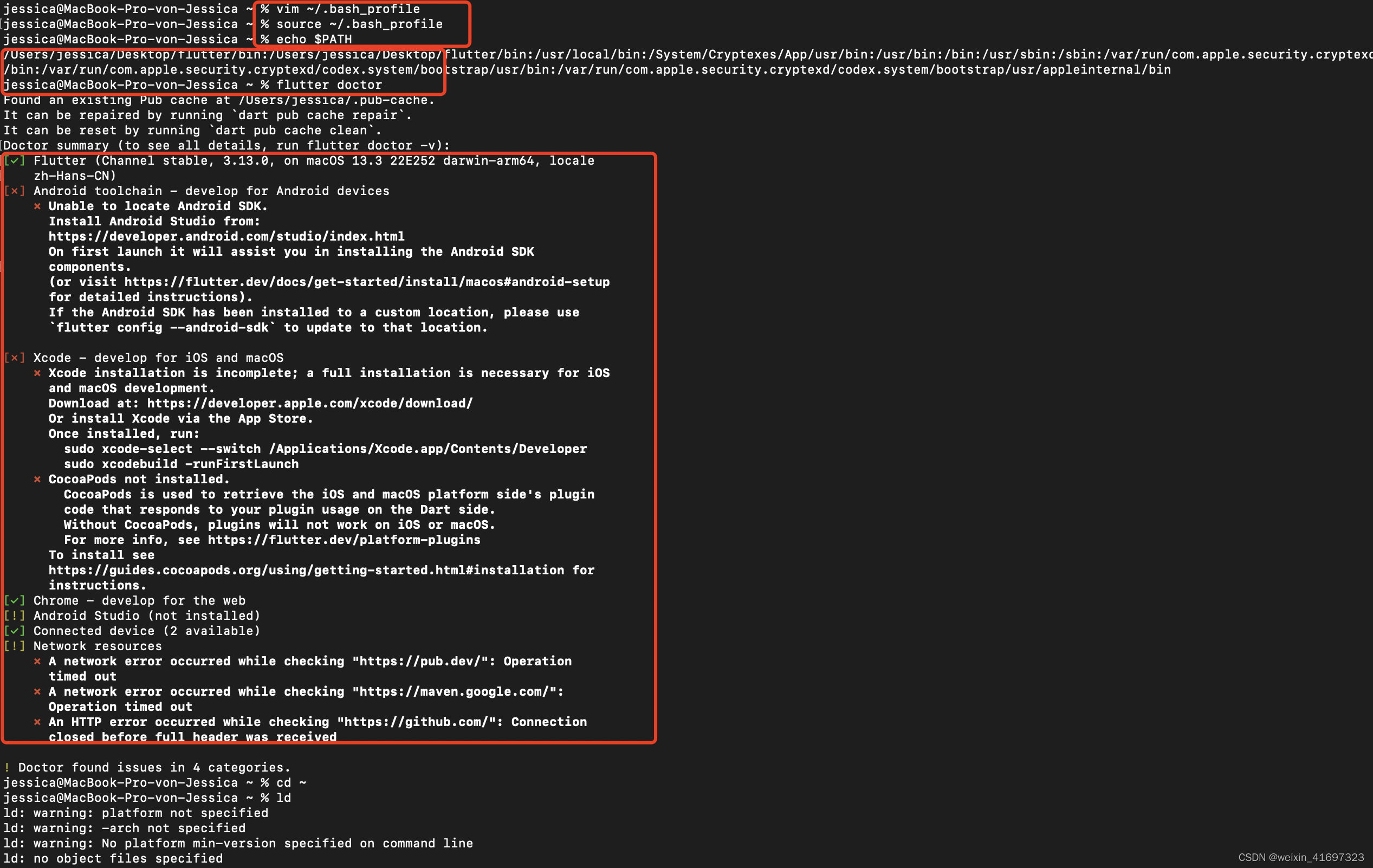
获取 Flutter SDK 下载以下安装包来获取最新的 stable Flutter SDK将文件解压到目标路径, 比如: cd ~/development $ unzip ~/Downloads/flutter_macos_3.13.0-stable.zip 配置 flutter 的 PATH 环境变量: export PATH"$PATH:pwd/flutter/bin" // 这个命…...
在外SSH远程连接macOS服务器
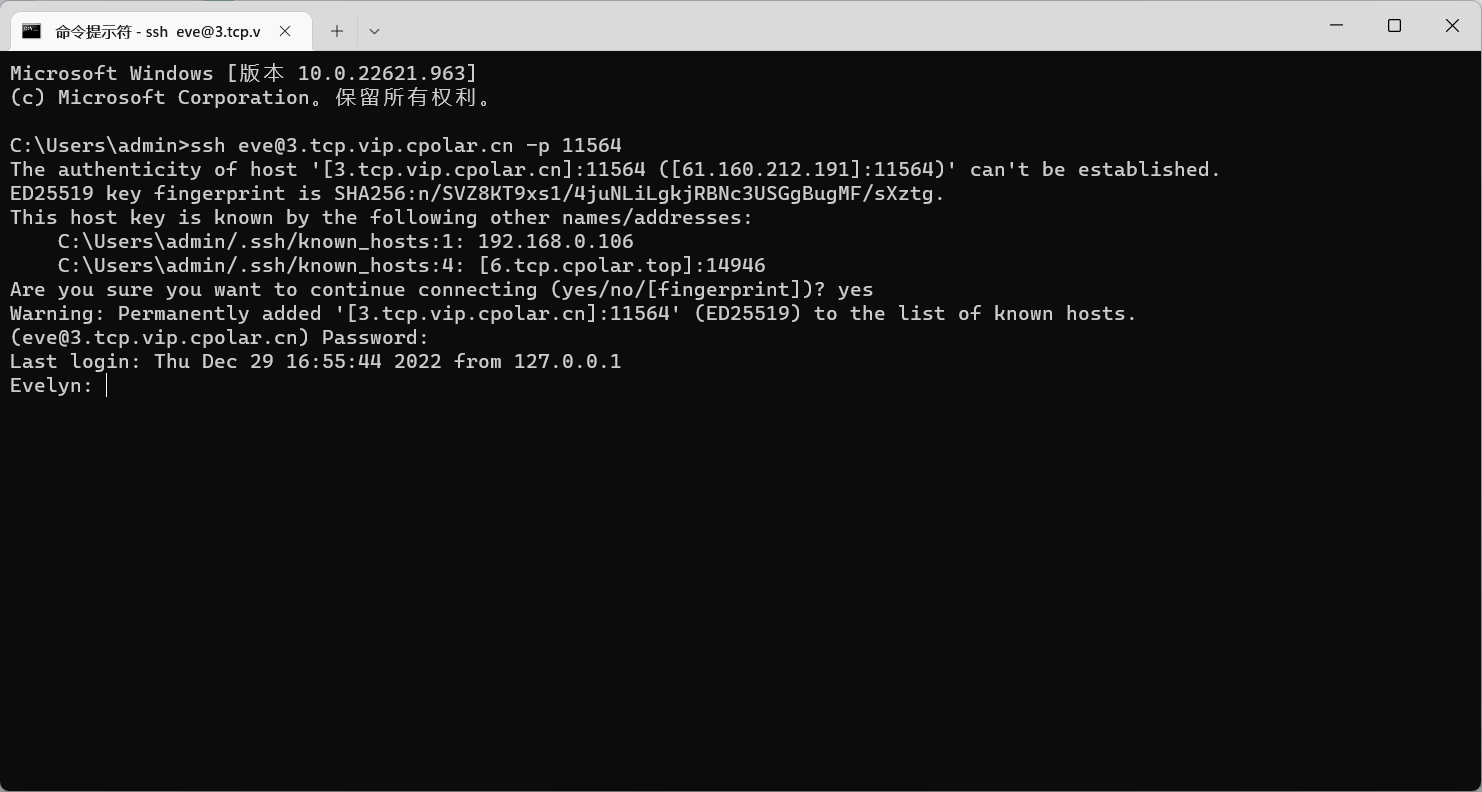
文章目录 前言1. macOS打开远程登录2. 局域网内测试ssh远程3. 公网ssh远程连接macOS3.1 macOS安装配置cpolar3.2 获取ssh隧道公网地址3.3 测试公网ssh远程连接macOS 4. 配置公网固定TCP地址4.1 保留一个固定TCP端口地址4.2 配置固定TCP端口地址 5. 使用固定TCP端口地址ssh远程 …...
Dockerfile文件详细
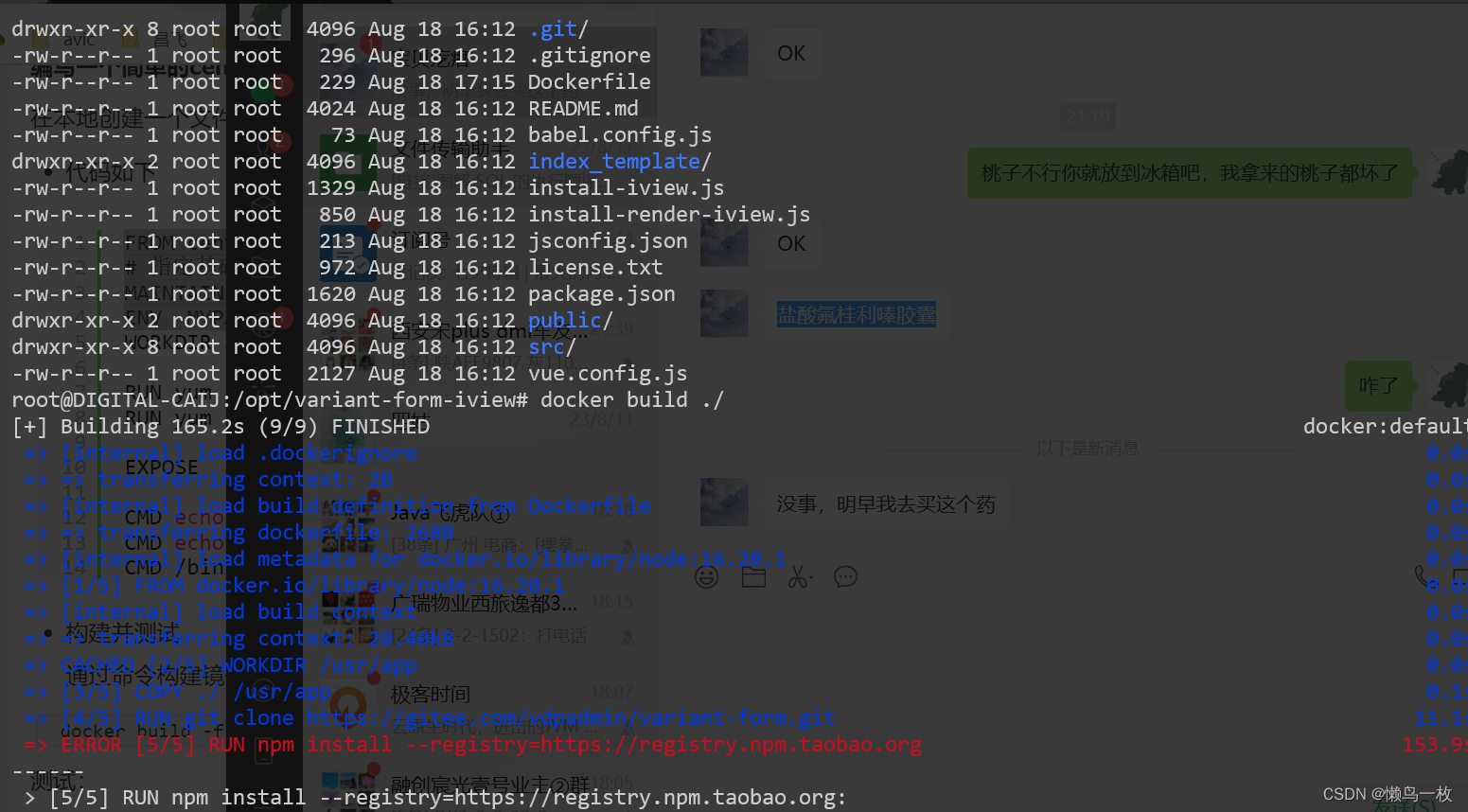
Dockerfile 是一个文本文件,里面包含组装新镜像时用到的基础镜像和各种指令,使用dockerfile 文件来定义镜像,然后运行镜像,启动容器。 dockerfile文件的组成部分 一个dockerfile文件包含以下部分: 基础镜像信息&…...

C语言学习系列-->看淡指针(3)
文章目录 一、字符指针变量二、数组指针变量2.1 概述2.2 数组指针初始化 三、二维数组传参本质四、函数指针五、typedef关键字六、函数指针数组 一、字符指针变量 在指针的类型中我们知道有⼀种指针类型为字符指针 char* 一般使用: #include<stdio.h>int main…...
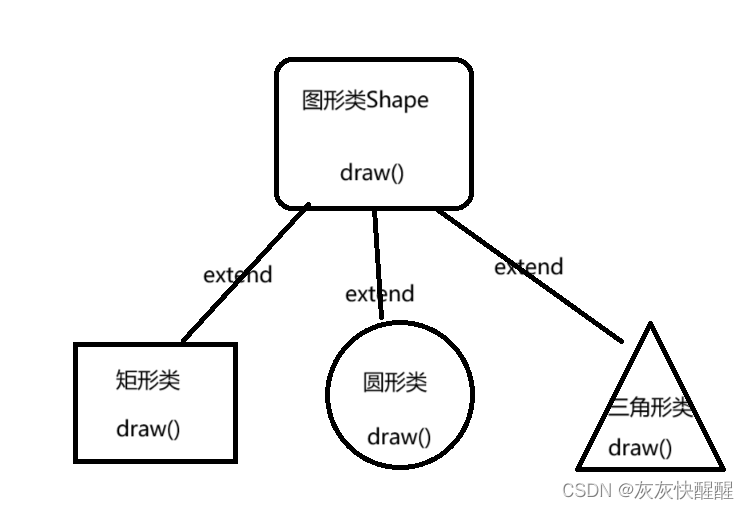
Java抽象类详解
抽象类 抽象类的概念 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是来描绘对象的,如果一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类。比如: 说…...
06-微信小程序-注册程序-场景值
06-微信小程序-注册程序 文章目录 注册小程序参数 Object object案例代码 场景值场景值作用场景值列表案例代码 注册小程序 每个小程序都需要在 app.js 中调用 App 方法注册小程序实例,绑定生命周期回调函数、错误监听和页面不存在监听函数等。 详细的参数含义和使…...
多种方法实现 Nginx 隐藏式跳转(隐式URL,即浏览器 URL 跳转后保持不变)
多种方法实现 Nginx 隐藏式跳转(隐式URL,即浏览器 URL 跳转后保持不变)。 一个新项目,后端使用 PHP 实现,前端不做路由,提供一个模板,由后端路由控制。 Route::get(pages/{name}, [\App\Http\Controllers\ResourceController::class, getResourceVersion])...

视频汇聚云平台EasyCVR视频监控管理平台进行SDN转推的操作步骤
视频汇聚/视频云存储/集中存储/视频监控管理平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,实现视频资源的鉴权管理、按需调阅、全网分发、云存储、智能分析等,视频智能分析平台EasyCVR融合性强、开放度…...

SQL 语句继续学习之记录二
三, 聚合与排序 对表进行聚合查询,即使用聚合函数对表中的列进行合计值或者平均值等合计操作。 通常,聚合函数会对null以外的对象进行合计。但是只有count 函数例外,使用count(*) 可以查出包含null在内的全部数据行数。 使用dis…...
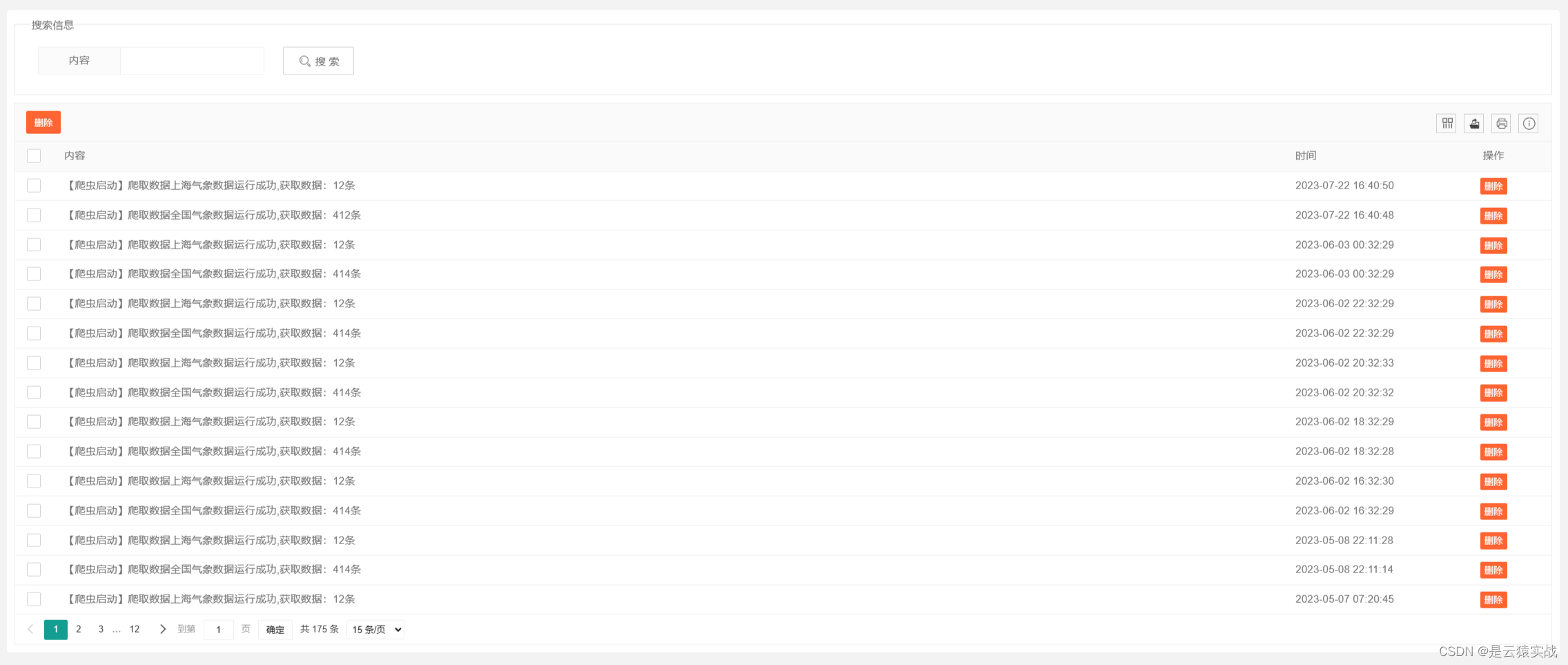
【Python原创设计】基于Python Flask 机器学习的全国+上海气象数据采集预测可视化系统-附下载链接以及详细论文报告,原创项目其他均为抄袭
基于Python Flask 机器学习的全国上海气象数据采集预测可视化系统 一、项目简介二、开发环境三、项目技术四、功能结构五、运行截图六、功能实现七、数据库设计八、源码获取 一、项目简介 在信息科技蓬勃发展的当代,我们推出了一款基于Python Flask的全国上海气象数…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
