SVM详解
公式太多了,就用图片用笔记呈现,SVM虽然算法本质一目了然,但其中用到的数学推导还是挺多的,其中拉格朗日约束关于α>0这块证明我看了很长时间,到底是因为悟性不够。对偶问题也是,用了一个简单的例子才明白,事实上,从简单的例子进行来理解更复杂的东西确实很舒服。核函数这块主要是正定核函数的证明需要看一下,K(x.z)=I(x)*I(z),先升维再求点积=先点积再升维。最后SMO,经典中的经典,看的我头疼,最主要的就是公式的推导。

















代码:
'''
原理解释:
支持向量为距离超平面最近的一个向量
而我们要寻找的是支持向量到超平面的最大距离
超平面可定义为W^T x +b=0 (参照二维直线方程ax+by+c=0)
二维空间点(x,y)到直线Ax+By+C=0的距离公式是:
|Ax+By+C|/(A^2+B^2)^(1/2)
扩展到n维空间后,点x=(x1,x2,x3,,,xn)到直线W^T x+b=0的距离为:
|W^T x+b|/||w||
其中||W||=(w1^2+...wn^2)^(1/2)
因为支持向量到超平面的距离是d,也是样本点到超平面的最短距离
所以
(W^T x+b)/||W||>=d,y=1
(W^T X+b)/||W||<=-d,y=-1
稍作转换可以得到:
(W^T x+b)/(||W||*d)>=1,y=1
(W^T X+b)/(||W||*d)<=-1,y=-1'''
from __future__ import print_function
from numpy import *
import matplotlib.pyplot as plt
class optStruct:'''建立的数据结构来保存所有的重要值'''def __init__(self,dataMatIn,classLabels,C,toler,kTup):'''Args:dataMatIn 数据集classLabels 类别标签C 松弛变量(常量值),允许有些数据点可以处于分割面的错误一侧控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重可以通过调节该参数达到不同的结果toler 容错率kTup 包含核函数信息的元组'''self.X=dataMatInself.labelMat=classLabelsself.C=Cself.tol=toler#数据的行数self.m=shape(dataMatIn)[0]self.alphas=mat(zeros((self.m,1)))self.b=0#误差缓存,第一列给出的是eCache是否有效的标志位,第二列给出的是实际的E值self.eCache=mat(zeros((self.m,2)))#m行m列的矩阵#m行m列的矩阵self.K=mat(zeros((self.m,self.m)))for i in range(self.m):self.K[:,i]=kernelTrans(self.X,self.X[i,:],kTup) def kernelTrans(X,A,kTup):# calc the kernel or transform data to a higher dimensional space"""核转换函数Args:X dataMatIn数据集A dataMatIn数据集的第i行的数据kTup 核函数的信息Returns:"""m,n=shape(X)K=mat(zeros((m,1)))if kTup[0]=='lin':#linear kernel: m*n * n*1=m*1K=X*A.Telif kTup[0]=='rbf':for j in range(m):deltaRow=X[j,:]-AK[j]=deltaRow*deltaRow.T#径向基函数的高斯版本K=exp(K/(-1*kTup[1]**2))#divide in numpy is element-wise not matrix like matlabelse:raise NameError('Houston We Have a Problem -- That Kernel is not recognized')return Kdef loadDataSet(fileName):'''loadDataSet(对文件进行逐行解析,从而得到第n行的类标签和整个数据矩阵)Args:fileName 文件名Returns:dataMat 数据矩阵labelMat 类标签'''dataMat = []labelMat=[]fr=open(fileName)for line in fr.readlines():lineArr=line.strip().split('\t')dataMat.append([float(lineArr[0]),float(lineArr[1])])labelMat.append(float(lineArr[2]))return dataMat,labelMatdef calcEk(oS,k):'''calcEk(求Ek误差:预测值-真实值的差)该过程在完整版的SMO算法中出现的次数较多,因此将其单独作为一个方法Args:oS optStruct对象k 具体的某一行Returns:Ek 预测结果与真实结果比对,计算误差Ek'''fXk=float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k]+oS.b) #E=apha*y*k+b-g(x)Ek=fXk-float(oS.labelMat[k])return Ekdef selectJrand(i,m):'''随机选择一个整数Args:i 第一个alpha的下标m 所有alpha的数目Returns:j 返回一个不为i的随机数,在0~m之间的整数值'''j=iwhile j==i:j=int(random.uniform(0,m))return jdef selectJ(i,oS,Ei): #this is the second choice -heurstic,and calcs Ej'''内循环的启发式方法选择第二个(内循环)alpha的alpha值这里的目标是选择合适的第二个alpha值以保证每次优化中采用的最大步长该函数的误差与第一个alpha值Ei和下标i有关Args:i 具体的第一行oS optStruct对象Ei 预测结果与真实性结果比对,计算误差EiReturns:j 随机选出的第j一行Ej 预测结果与真实结果比对,计算误差Ej'''maxK=-1maxDeltaE=0Ej=0#首先将输入值Ei在缓存中设置成为有效的,这里的有效意味着它已经计算好了oS.eCache[i]=[1,Ei]# print ('oS.ecache[%s]=%s' %(i,oS.eCache[i]))#print ('oS.eCache[:,0].A=%s'%oS.eCache[:,0].A.T)###返回非0的:行列值# nonzero(oS.eCache[:,0].A)=(# 行: array([ 0, 2, 4, 5, 8, 10, 17, 18, 20, 21, 23, 25, 26, 29, 30, 39, 46,52, 54, 55, 62, 69, 70, 76, 79, 82, 94, 97]), # 列: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0])#)# print('nonzero(oS.eCache[:,0].A)=',nonzero(oS.eCache[:,0].A))# # 取行的list# print('nonzero(oS.eCache[:,0].A)[0]=',nonzero(oS.eCache[:,0].A)[0])# 非零E值的行的list列表,所对应的alpha值validEcacheList=nonzero(oS.eCache[:,0].A)[0]if(len(validEcacheList))>1:for k in validEcacheList: #在所有的值上进行循环,并选择其中使得改变最大的那个值if k==i:continue #don't calc for i,waste of time#求Ek误差: 预测值-真实值的差Ek=calcEk(oS,k)deltaE=abs(Ei-Ek)if(deltaE>maxDeltaE):#选择具有最大步长的jmaxK=kmaxDeltaE=deltaEEj=Ekreturn maxK,Ejelse: #如果是第一次循环,则随机选择一个alpha值j=selectJrand(i,oS.m)#求Ek误差:预测值-真实值的差Ej=calcEk(oS,j)return j,Ejdef updateEk(oS,k):"""updateEk(计算误差值并存入缓存中。)在对alpha值进行优化之后会用到这个值。Args:oS optStruct对象k 某一列的行号"""# 求 误差: 预测值-真实值的差 Ek=calcEk(oS,k)oS.eCache[k]=[1,Ek]def clipAlpha(aj,H,L):'''clipAlpha(调整aj的值,使aj处于 L<=aj<=H)Args:aj 目标值H 最大值L 最小值Returns:aj 目标值'''if aj>H:aj=Hif L>aj:aj=Lreturn ajdef innerL(i,oS):'''innerL内循环代码Args:i 具体的某一行oS optStruct对象Returns:0 找不到最优的值1 找到了最优的值,并且oS.Cache到缓存中'''# 求Ek误差:预测值-真实值的差Ei=calcEk(oS,i)# 约束条件(KKT条件是解决最优化问题时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值)# 0<=alphas[i]<=C,但由于0和C是边界值,我们无法进行优化,因为需要增加一个alphas和降低一个alphas# 表示发生错误的概率:labelMat[i]*Ei 如果超出了toler,才需要优化,至于正负号,我们考虑绝对值就对了'''# 检验训练样本(xi, yi)是否满足KKT条件yi*f(i) >= 1 and alpha = 0 (outside the boundary)yi*f(i) == 1 and 0<alpha< C (on the boundary)yi*f(i) <= 1 and alpha = C (between the boundary)'''if((oS.labelMat[i]*Ei<-oS.tol)and (oS.alphas[i]<oS.C)) or ((oS.labelMat[i]*Ei>oS.tol) and (oS.alphas[i]>0)):#选择最大的误差对应的j进行优化,效果更明显j,Ej=selectJ(i,oS,Ei)alphaIold=oS.alphas[i].copy()alphaJold=oS.alphas[j].copy()#L和H用于将alphas[j]调整到0-C之间,如果L==H,就不做任何改变,直接return 0if(oS.labelMat[i]!=oS.labelMat[j]):L=max(0,oS.alphas[j]-oS.alphas[i])H=min(oS.C,oS.C+oS.alphas[j]-oS.alphas[i])else:L=max(0,oS.alphas[i]+oS.alphas[j]-oS.C)H=min(oS.C,oS.alphas[j]+oS.alphas[i])if L==H:# print("L==H")return 0# eta是alphas[j]的最优修改量,如果eta==0,需要退出for循环的当前迭代过程#参考《统计学习方法》李航-P125~P128<序列最小最优化算法>eta=2.0*oS.K[i,j]-oS.K[i,i]-oS.K[j,j] #changed for kernelif eta>=0:print("eta>=0")return 0#计算出一个新的alphas[j]值oS.alphas[j]-=oS.labelMat[j]*(Ei-Ej)/eta#并使用辅助函数,以及L和H对其进行调整oS.alphas[j]=clipAlpha(oS.alphas[j],H,L)#更新误差缓存updateEk(oS,j)# 检查alpha[j]是否只是轻微的改变,如果是的话,就退出for循环if(abs(oS.alphas[j]-alphaJold)<0.00001):# print("j not moving enough")return 0#然后alphas[i]和alphas[j]同样进行改变,虽然改变的大小不一样,但是改变的方向正好相反oS.alphas[i]+=oS.labelMat[j]*oS.labelMat[i]*(alphaJold-oS.alphas[j])#更新误差缓存updateEk(oS,i)# 在对alpha[i],alpha[j] 进行优化之后,给这两个alpha值设置一个常数b# w= Σ[1~n] ai*yi*xi => b = yi- Σ[1~n] ai*yi(xi*xj)# 所以:b1-b=(y1-y)- Σ[1~n] yi*(a1-a)*(xi*x1)# 为什么减2遍?因为是减去Σ[1~n],正好2个变量i和j,所以减2遍b1=oS.b-Ei-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i]-oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]b2=oS.b-Ej-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]-oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]if(0<oS.alphas[i])and (oS.C>oS.alphas[i]):oS.b=b1elif (0<oS.alphas[j])and (oS.C>oS.alphas[j]):oS.b=b2else:oS.b=(b1+b2)/2.0return 1else:return 0def smoP(dataMatIn,classLabels,C,toler,maxIter,kTup=('lin',0)):'''完整SMO算法外循环,与smoSimple有些类似,但这里的循环退出条件更多一些Args:dataMatIn 数据集classLabels 类别标签C 松弛变量(常量值),允许有些数据点可以处于分隔面的错误一侧。控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。可以通过调节该参数达到不同的结果。toler 容错率maxIter 退出前最大的循环次数kTup 包含核函数信息的元组Returns:b 模型的常量值alphas 拉格朗日乘子'''# 创建一个optStruct 对象oS=optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler,kTup)iter=0entireSet=TruealphaPairsChanged=0# 循环遍历:循环maxIter次 并且(alphaPairsChanged存在可以改变 or所有行遍历一遍)while(iter<maxIter) and ((alphaPairsChanged>0)or (entireSet)):alphaPairsChanged=0# 当entireSet=true or 非边界alpha对没有了:就开始寻找alpha对,然后决定是否要进行else。if entireSet:# 在数据集上遍历所有可能的alphafor i in range(oS.m):#是否存在alpha对,存在就+1alphaPairsChanged+=innerL(i,oS)# print("fullSet,iter: %d i:%d,pairs changed %d" %(iter,i,clphaPairsChanged))iter+=1#对已存在alpha对,选出非边界的alpha值,进行优化else:#遍历所有的非边界alpha值,也就是不在边界0或C上的值nonBoundIs=nonzero((oS.alphas.A>0)*(oS.alphas.A<C))[0]for i in nonBoundIs:alphaPairsChanged+=innerL(i,oS)# print("non-bound,iter:%d i:%d,pairs changed %d"%(iter,i,alphaPairsChanged))iter+=1# 如果找到alpha对,就优化非边界alpha值,否则,就重新进行寻找,如果寻找一遍 遍历所有的行还是没找到,就退出循环if entireSet:entireSet=False #toggle entire set loopelif(alphaPairsChanged==0):entireSet=Trueprint("iteration number: %d" % iter)return oS.b,oS.alphasdef calcWs(alphas,dataArr,classLabels):'''基于alpha计算w值Args:alphas 拉格朗日乘子dataArr feature数据集classLabels 目标变量数据集Returns:wc 回归系数'''X=mat(dataArr)labelMat=mat(classLabels).transpose()m,n=shape(X)w=zeros((n,1))for i in range(m):w+=multiply(alphas[i]*labelMat[i],X[i,:].T)return wdef testRbf(k1=1.3):dataArr,labelArr=loadDataSet('6.SVM/testSetRBF.txt')b,alphas=smoP(dataArr,labelArr,200,0.0001,10000,('rbf',k1))#C=200 importantdatMat=mat(dataArr)labelMat=mat(labelArr).transpose()svInd=nonzero(alphas.A>0)[0]sVs=datMat[svInd] # get matrix of only support vectorslabelSV=labelMat[svInd]print("there are %d Support Vectors"% shape(sVs)[0])m,n=shape(datMat)errorCount=0for i in range(m):kernelEval=kernelTrans(sVs,datMat[i,:],('rbf',k1))# 和这个svm-simple类似: fxi=float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T))+bpredict=kernelEval.T*multiply(labelSV,alphas[svInd])+bif sign(predict)!=sign(labelArr[i]):errorCount+=1print("the training error rate is : %f" %(float(errorCount)/m))dataArr,labelArr=loadDataSet('6.SVM/testSetRBF2.txt')errorCount=0datMat=mat(dataArr)labelMat=mat(labelArr).transpose()m,n=shape(datMat)for i in range(m):kernelEval=kernelTrans(sVs,datMat[i,:],('rbf',k1))predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b #w=Σalpha*y*x y=w*x+bif sign(predict)!=sign(labelArr[i]):errorCount+=1print("the test error rate is : %f"%(float(errorCount)/m))ws=calcWs(alphas,dataArr,labelArr)plotfig_SVM(dataArr,labelArr,ws,b,alphas)def img2vector(filename):returnVect=zeros((1,1024))fr=open(filename)for i in range(32):lineStr=fr.readline()for j in range(32):returnVect[0,32*i+j]=int(lineStr[j])return returnVectdef loadImages(dirName):from os import listdirhwLabels=[]print(dirName)trainingFileList=listdir(dirName)#load the training setm=len(trainingFileList)trainingMat=zeros((m,1024))for i in range(m):fileNameStr=trainingFileList[i]fileStr=fileNameStr.split('.')[0]classNumber=int(fileStr.split('_')[0])if classNumber==9:hwLabels.append(-1)else:hwLabels.append(1)trainingMat[i, :] = img2vector('%s/%s' % (dirName, fileNameStr))return trainingMat, hwLabelsdef testDigits(kTup=('rbf',10)):#1.导入训练数据dataArr,labelArr=loadImages('6.SVM/trainingDigits')b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)datMat=mat(dataArr)labelMat=mat(labelArr).transpose()svInd=nonzero(alphas.A>0)[0]sVs=datMat[svInd]labelSV=labelMat[svInd]# print("there are %d Support Vectors"% shape(sVs)[0])m,n=shape(datMat)errorCount=0for i in range(m):kernelEval = kernelTrans(sVs, datMat[i, :], kTup)# 1*m * m*1 = 1*1 单个预测结果predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + bif sign(predict) != sign(labelArr[i]): errorCount += 1print("the training error rate is: %f" % (float(errorCount) / m))# 2. 导入测试数据dataArr, labelArr = loadImages('6.SVM/testDigits')errorCount = 0datMat = mat(dataArr)labelMat = mat(labelArr).transpose()m, n = shape(datMat)for i in range(m):kernelEval = kernelTrans(sVs, datMat[i, :], kTup)predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + bif sign(predict) != sign(labelArr[i]): errorCount += 1print("the test error rate is: %f" % (float(errorCount) / m)) ws=calcWs(alphas,dataArr,labelArr)plotfig_SVM(dataArr,labelArr,ws,b,alphas)def plotfig_SVM(xArr,yArr,ws,b,alphas):'''参考地址: http://blog.csdn.net/maoersong/article/details/24315633http://www.cnblogs.com/JustForCS/p/5283489.htmlhttp://blog.csdn.net/kkxgx/article/details/6951959'''xMat=mat(xArr)yMat=mat(yArr)# b 原来是矩阵,先转为数组类型后其数组大小为(1,1),所以后面加【0】,变为(1,)b=array(b)[0]fig=plt.figure()ax=fig.add_subplot(111)#注意flatten的用法ax.scatter(xMat[:,0].flatten().A[0],xMat[:,1].flatten().A[0])#x最大值,最小值根据原数据集dataArr[:0]的大小而定x=arange(-1.0,10.0,0.1)#根据x.w+b=0 得到,其式子展开为w0.x1+w1.x2+b=0,x2就是y值y=(-b-ws[0,0]*x)/ws[1,0]ax.plot(x,y)for i in range(shape(yMat[0, :])[1]):if yMat[0, i] > 0:ax.plot(xMat[i, 0], xMat[i, 1], 'cx')else:ax.plot(xMat[i, 0], xMat[i, 1], 'kp')# 找到支持向量,并在图中标红for i in range(100):if alphas[i] > 0.0:ax.plot(xMat[i, 0], xMat[i, 1], 'ro')plt.show()#无核函数测试
#获取特征和目标变量
dataArr,labelArr=loadDataSet('6.SVM/testSet.txt')
#print labelArr#b是常量值,alphas是拉格朗日乘子
b,alphas=smoP(dataArr,labelArr,0.6,0.001,40)
print('/n/n/n')
print('b=',b)
print('alphas[alphas>0]=',alphas[alphas>0])
print('shape(alphas[alphas>0])=',shape(alphas[alphas>0]))
for i in range(100):if alphas[i]>0:print(dataArr[i],labelArr[i])
#画图
ws=calcWs(alphas,dataArr,labelArr)
plotfig_SVM(dataArr,labelArr,ws,b,alphas)#有核函数测试
testRbf(0.8)#项目实战
#手写数字识别
testDigits(('rbf', 0.2))#sklearn库的运用
from __future__ import print_function
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svmprint(__doc__)# 创建40个分离点
np.random.seed(0)
#X=np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]]
#Y=[0]*20+[1]*20def loadDataSet(fileName):'''对文件进行逐行解析,从而得到第n行的类标签和整个数据矩阵Args:fileName 文件名Returns:dataMat 数据矩阵labelMat 类标签'''dataMat=[]labelMat=[]fr=open(fileName)for line in fr.readlines():lineArr=line.strip().split('\t')dataMat.append([float(lineArr[0]),float(lineArr[1])])labelMat.append(float(lineArr[2]))return dataMat,labelMatX,Y=loadDataSet('6.SVM/testSet.txt')
X=np.mat(X)print("X=",X)
print("Y=",Y)#拟合一个SVM模型
clf=svm.SVC(kernel='linear')
clf.fit(X,Y)#获取分割超平面
w=clf.coef_[0]
#斜率
a=-w[0]/w[1]
# 从-5倒5,顺序间隔采样50个样本,默认是num=50
# xx=np.linspace(-5,5) # ,num=50)
xx=np.linspace(-2,10) # ,num=50)
#二维的直线方程
yy=a*xx-(clf.intercept_[0])/w[1]
print("yy=",yy)# plot the parallels to the separating hyperplane that pass through the support vectors
# 通过支持向量绘制分割超平面
print("support_vectors_=",clf.support_vectors_)
b=clf.support_vectors_[0]
yy_down=a*xx+(b[1]-a*b[0])
b=clf.support_vectors_[-1]
yy_up=a*xx+(b[1]-a*b[0])# plot the line, the points, and the nearest vectors to the plane
plt.plot(xx,yy,'k-')
plt.plot(xx,yy_down,'k--')
plt.plot(xx,yy_up,'k--')plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80,facecolors='none')
plt.scatter([X[:, 0]], [X[:, 1]])plt.axis('tight')
plt.show()
以上为jupyter实现
相关文章:

SVM详解
公式太多了,就用图片用笔记呈现,SVM虽然算法本质一目了然,但其中用到的数学推导还是挺多的,其中拉格朗日约束关于α>0这块证明我看了很长时间,到底是因为悟性不够。对偶问题也是,用了一个简单的例子才明…...
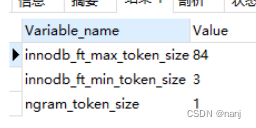
mysql全文检索使用
数据库数据量10万左右,使用like %test%要耗费30秒左右,放弃该办法 使用mysql的全文检索 第一步:建立索引 首先修改一下设置: my.ini中ngram_token_size 1 可以通过 show variables like %token%;来查看 接下来建立索引:alter table 表名 add f…...

opencv 进阶17-使用K最近邻和比率检验过滤匹配(图像匹配)
K最近邻(K-Nearest Neighbors,简称KNN)和比率检验(Ratio Test)是在计算机视觉中用于特征匹配的常见技术。它们通常与特征描述子(例如SIFT、SURF、ORB等)一起使用,以在图像中找到相似…...
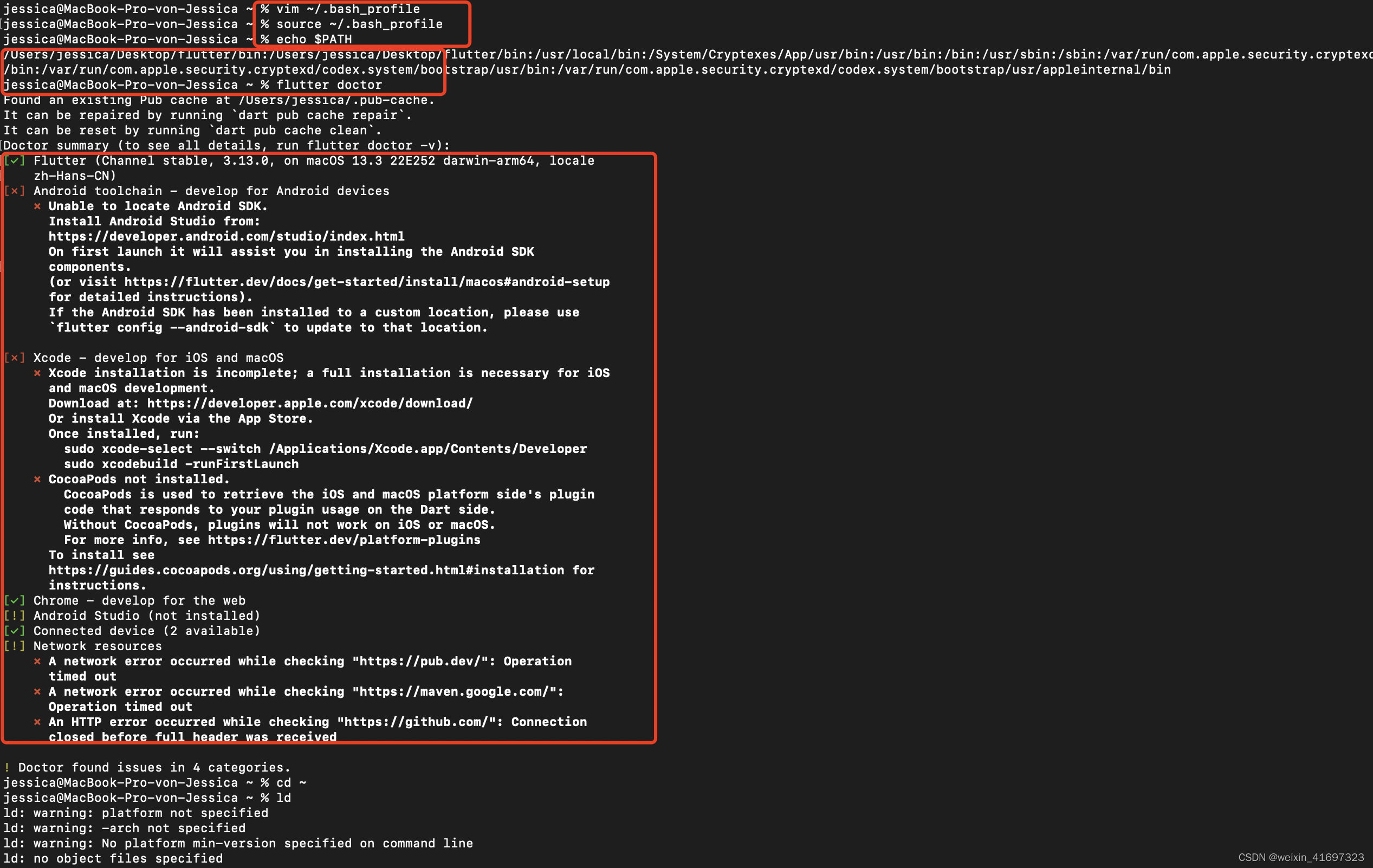
Mac Flutter web环境搭建
获取 Flutter SDK 下载以下安装包来获取最新的 stable Flutter SDK将文件解压到目标路径, 比如: cd ~/development $ unzip ~/Downloads/flutter_macos_3.13.0-stable.zip 配置 flutter 的 PATH 环境变量: export PATH"$PATH:pwd/flutter/bin" // 这个命…...
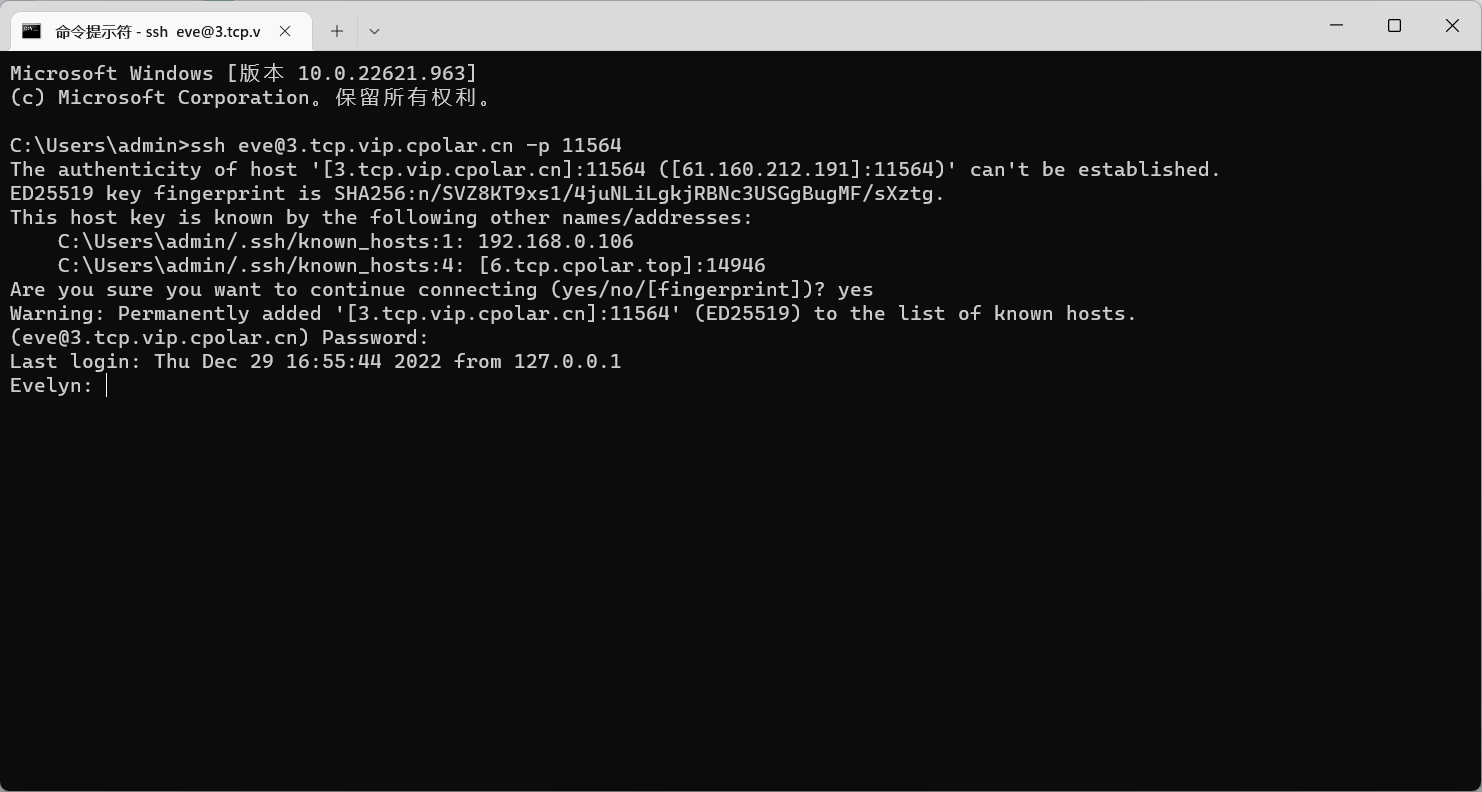
在外SSH远程连接macOS服务器
文章目录 前言1. macOS打开远程登录2. 局域网内测试ssh远程3. 公网ssh远程连接macOS3.1 macOS安装配置cpolar3.2 获取ssh隧道公网地址3.3 测试公网ssh远程连接macOS 4. 配置公网固定TCP地址4.1 保留一个固定TCP端口地址4.2 配置固定TCP端口地址 5. 使用固定TCP端口地址ssh远程 …...
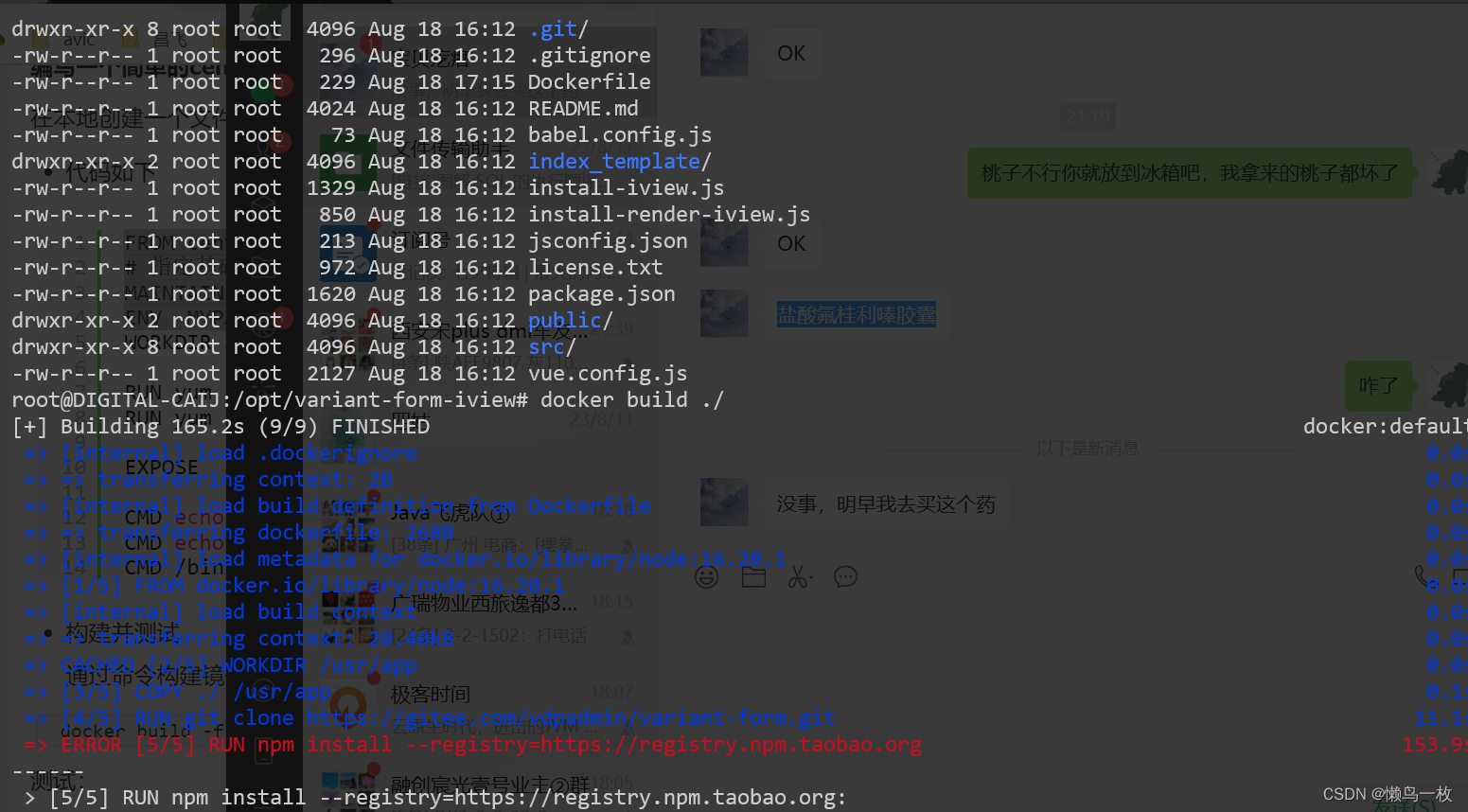
Dockerfile文件详细
Dockerfile 是一个文本文件,里面包含组装新镜像时用到的基础镜像和各种指令,使用dockerfile 文件来定义镜像,然后运行镜像,启动容器。 dockerfile文件的组成部分 一个dockerfile文件包含以下部分: 基础镜像信息&…...

C语言学习系列-->看淡指针(3)
文章目录 一、字符指针变量二、数组指针变量2.1 概述2.2 数组指针初始化 三、二维数组传参本质四、函数指针五、typedef关键字六、函数指针数组 一、字符指针变量 在指针的类型中我们知道有⼀种指针类型为字符指针 char* 一般使用: #include<stdio.h>int main…...
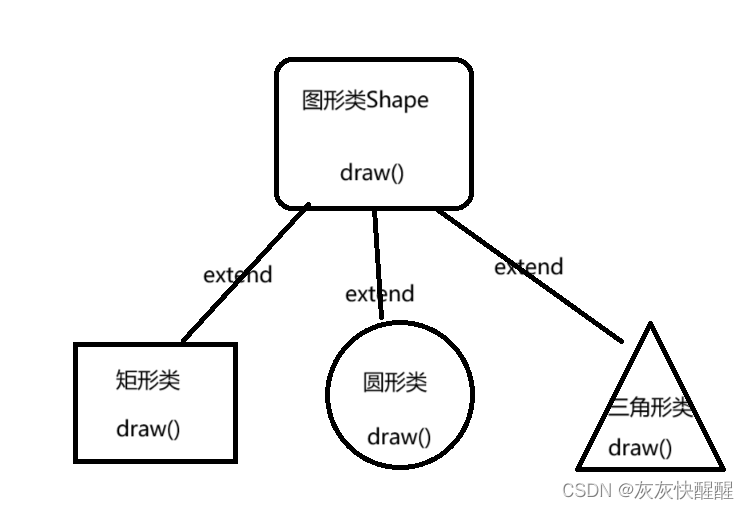
Java抽象类详解
抽象类 抽象类的概念 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是来描绘对象的,如果一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类。比如: 说…...
06-微信小程序-注册程序-场景值
06-微信小程序-注册程序 文章目录 注册小程序参数 Object object案例代码 场景值场景值作用场景值列表案例代码 注册小程序 每个小程序都需要在 app.js 中调用 App 方法注册小程序实例,绑定生命周期回调函数、错误监听和页面不存在监听函数等。 详细的参数含义和使…...
多种方法实现 Nginx 隐藏式跳转(隐式URL,即浏览器 URL 跳转后保持不变)
多种方法实现 Nginx 隐藏式跳转(隐式URL,即浏览器 URL 跳转后保持不变)。 一个新项目,后端使用 PHP 实现,前端不做路由,提供一个模板,由后端路由控制。 Route::get(pages/{name}, [\App\Http\Controllers\ResourceController::class, getResourceVersion])...

视频汇聚云平台EasyCVR视频监控管理平台进行SDN转推的操作步骤
视频汇聚/视频云存储/集中存储/视频监控管理平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,实现视频资源的鉴权管理、按需调阅、全网分发、云存储、智能分析等,视频智能分析平台EasyCVR融合性强、开放度…...

SQL 语句继续学习之记录二
三, 聚合与排序 对表进行聚合查询,即使用聚合函数对表中的列进行合计值或者平均值等合计操作。 通常,聚合函数会对null以外的对象进行合计。但是只有count 函数例外,使用count(*) 可以查出包含null在内的全部数据行数。 使用dis…...
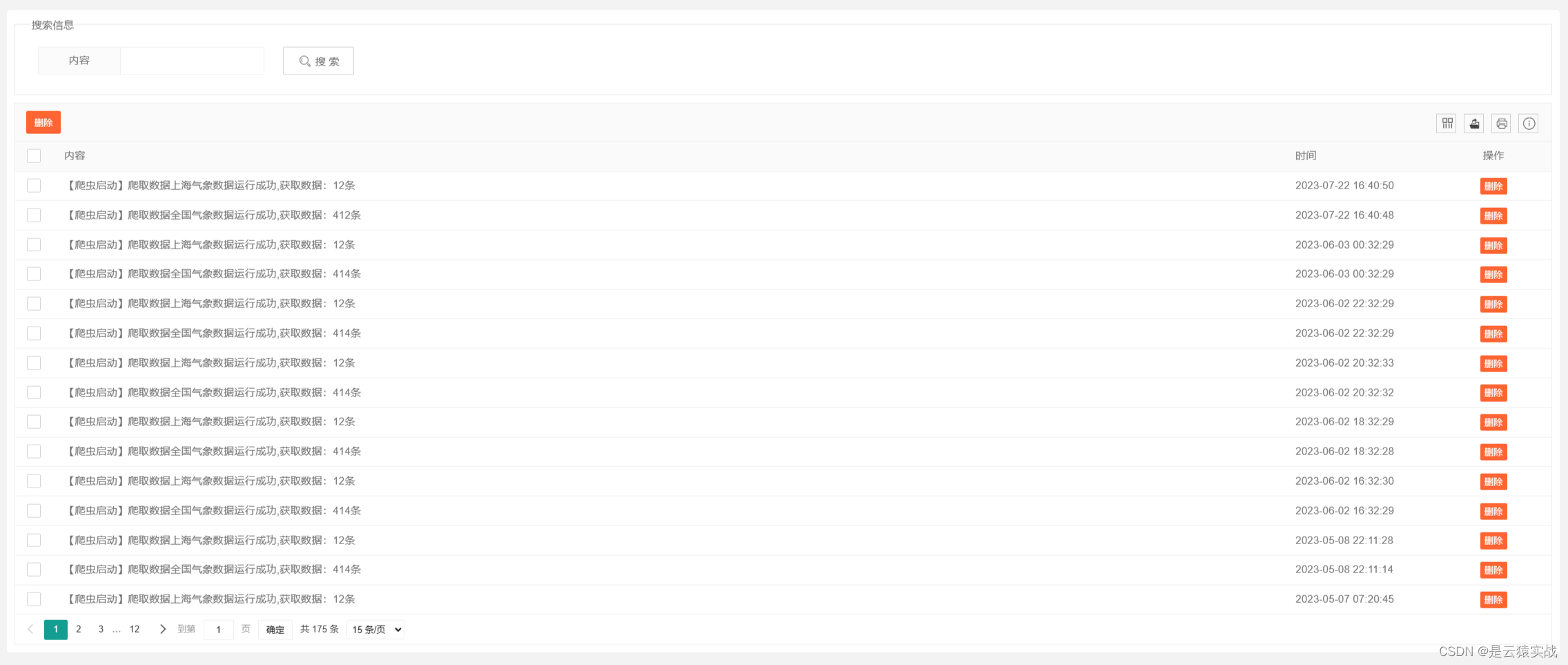
【Python原创设计】基于Python Flask 机器学习的全国+上海气象数据采集预测可视化系统-附下载链接以及详细论文报告,原创项目其他均为抄袭
基于Python Flask 机器学习的全国上海气象数据采集预测可视化系统 一、项目简介二、开发环境三、项目技术四、功能结构五、运行截图六、功能实现七、数据库设计八、源码获取 一、项目简介 在信息科技蓬勃发展的当代,我们推出了一款基于Python Flask的全国上海气象数…...

Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四)
文章目录 Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四)服务端客户端 Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四) 服务端 服务端结构如下: UserModel using System; using System.Collections.Generic; usin…...

【Go 基础篇】Go语言获取用户终端输入:实现交互式程序的关键一步
介绍 在许多编程场景中,我们需要编写交互式程序,以便用户可以在终端中输入数据并与程序进行交互。Go语言提供了丰富的方式来获取用户终端输入,使得编写交互式程序变得简单而有趣。本篇博客将深入探讨Go语言中获取用户终端输入的各种方法&…...

学习笔记:Opencv实现拉普拉斯图像锐化算法
2023.8.19 为了在暑假内实现深度学习的进阶学习,Copy大神的代码,记录学习日常 图像锐化的百科: 图像锐化算法-sharpen_lemonHe_的博客-CSDN博客 在环境配置中要配置opencv: pip install opencv-contrib-python Code and lena.png…...

如何在前端实现WebSocket发送和接收UDP消息(多线程模式)
目录 简介:步骤1:创建WebSocket连接步骤2:创建Web Workers步骤3:发送和接收UDP消息(多线程模式)结束语: 简介: 本文将继续介绍如何在前端应用中利用WebSocket技术发送和接收UDP消息…...

【微服务】一文了解 Nacos
一文了解 Nacos Nacos 在阿里巴巴起源于 2008 2008 2008 年五彩石项目(完成微服务拆分和业务中台建设),成长于十年双十一的洪峰考验,沉淀了简单易用、稳定可靠、性能卓越的核心竞争力。 随着云计算兴起, 2018 2018 20…...

量子计算对信息安全的影响:探讨量子计算技术对现有加密方法和信息安全基础设施可能带来的颠覆性影响,以及应对策略
第一章:引言 随着科技的迅猛发展,量子计算作为一项颠覆性的技术正逐渐走入我们的视野。量子计算以其强大的计算能力引发了全球科技界的广泛关注。然而,正如硬币的两面,量子计算技术所带来的不仅仅是计算能力的巨大飞跃࿰…...

ajax-axios-url-form-serialize 插件
AJAX AJAX 概念 1.什么是 AJAX ? mdn 使用浏览器的 XMLHttpRequest 对象 与服务器通信 浏览器网页中,使用 AJAX技术(XHR对象)发起获取省份列表数据的请求,服务器代码响应准备好的省份列表数据给前端,前端拿到数据数…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
