学习笔记:Opencv实现拉普拉斯图像锐化算法
2023.8.19
为了在暑假内实现深度学习的进阶学习,Copy大神的代码,记录学习日常
图像锐化的百科:
图像锐化算法-sharpen_lemonHe_的博客-CSDN博客
在环境配置中要配置opencv:
pip install opencv-contrib-python
Code and lena.png:注意你是否在data下由lena.png
# -*- coding: utf-8 -*-
# Author : Vincent
# Time : 2018-05-19
# Func : Laplacian Sharpenfrom PIL import Image
import numpy as np# 读入原图像
img = Image.open('./data/lena.png')
# img.show()# 为了减少计算的维度,因此将图像转为灰度图
img_gray = img.convert('L')
img_gray.show()# 得到转换后灰度图的像素矩阵
img_arr = np.array(img_gray)
h = img_arr.shape[0] # 行
w = img_arr.shape[1] # 列# 拉普拉斯算子锐化图像,用二阶微分
new_img_arr = np.zeros((h, w)) # 拉普拉斯锐化后的图像像素矩阵
for i in range(2, h-1):for j in range(2, w-1):new_img_arr[i][j] = img_arr[i+1, j] + img_arr[i-1, j] + \img_arr[i, j+1] + img_arr[i, j-1] - \4*img_arr[i, j]# 拉普拉斯锐化后图像和原图像相加
laplace_img_arr = np.zeros((h, w)) # 拉普拉斯锐化图像和原图像相加所得的像素矩阵
for i in range(0, h):for j in range(0, w):laplace_img_arr[i][j] = new_img_arr[i][j] + img_arr[i][j]img_laplace = Image.fromarray(np.uint8(new_img_arr))
img_laplace.show()img_laplace2 = Image.fromarray(np.uint8(laplace_img_arr))
img_laplace2.show()
附上lena.png
效果所示(解读):
第一张lena是将三通道的RGB图转换为单通道的灰度图,第二张lena是用二阶拉普拉斯微分算子锐化的图像,第三张lena是用拉普拉斯锐化后图像和原图像相加所得的图像



相关文章:

学习笔记:Opencv实现拉普拉斯图像锐化算法
2023.8.19 为了在暑假内实现深度学习的进阶学习,Copy大神的代码,记录学习日常 图像锐化的百科: 图像锐化算法-sharpen_lemonHe_的博客-CSDN博客 在环境配置中要配置opencv: pip install opencv-contrib-python Code and lena.png…...

如何在前端实现WebSocket发送和接收UDP消息(多线程模式)
目录 简介:步骤1:创建WebSocket连接步骤2:创建Web Workers步骤3:发送和接收UDP消息(多线程模式)结束语: 简介: 本文将继续介绍如何在前端应用中利用WebSocket技术发送和接收UDP消息…...

【微服务】一文了解 Nacos
一文了解 Nacos Nacos 在阿里巴巴起源于 2008 2008 2008 年五彩石项目(完成微服务拆分和业务中台建设),成长于十年双十一的洪峰考验,沉淀了简单易用、稳定可靠、性能卓越的核心竞争力。 随着云计算兴起, 2018 2018 20…...

量子计算对信息安全的影响:探讨量子计算技术对现有加密方法和信息安全基础设施可能带来的颠覆性影响,以及应对策略
第一章:引言 随着科技的迅猛发展,量子计算作为一项颠覆性的技术正逐渐走入我们的视野。量子计算以其强大的计算能力引发了全球科技界的广泛关注。然而,正如硬币的两面,量子计算技术所带来的不仅仅是计算能力的巨大飞跃࿰…...

ajax-axios-url-form-serialize 插件
AJAX AJAX 概念 1.什么是 AJAX ? mdn 使用浏览器的 XMLHttpRequest 对象 与服务器通信 浏览器网页中,使用 AJAX技术(XHR对象)发起获取省份列表数据的请求,服务器代码响应准备好的省份列表数据给前端,前端拿到数据数…...
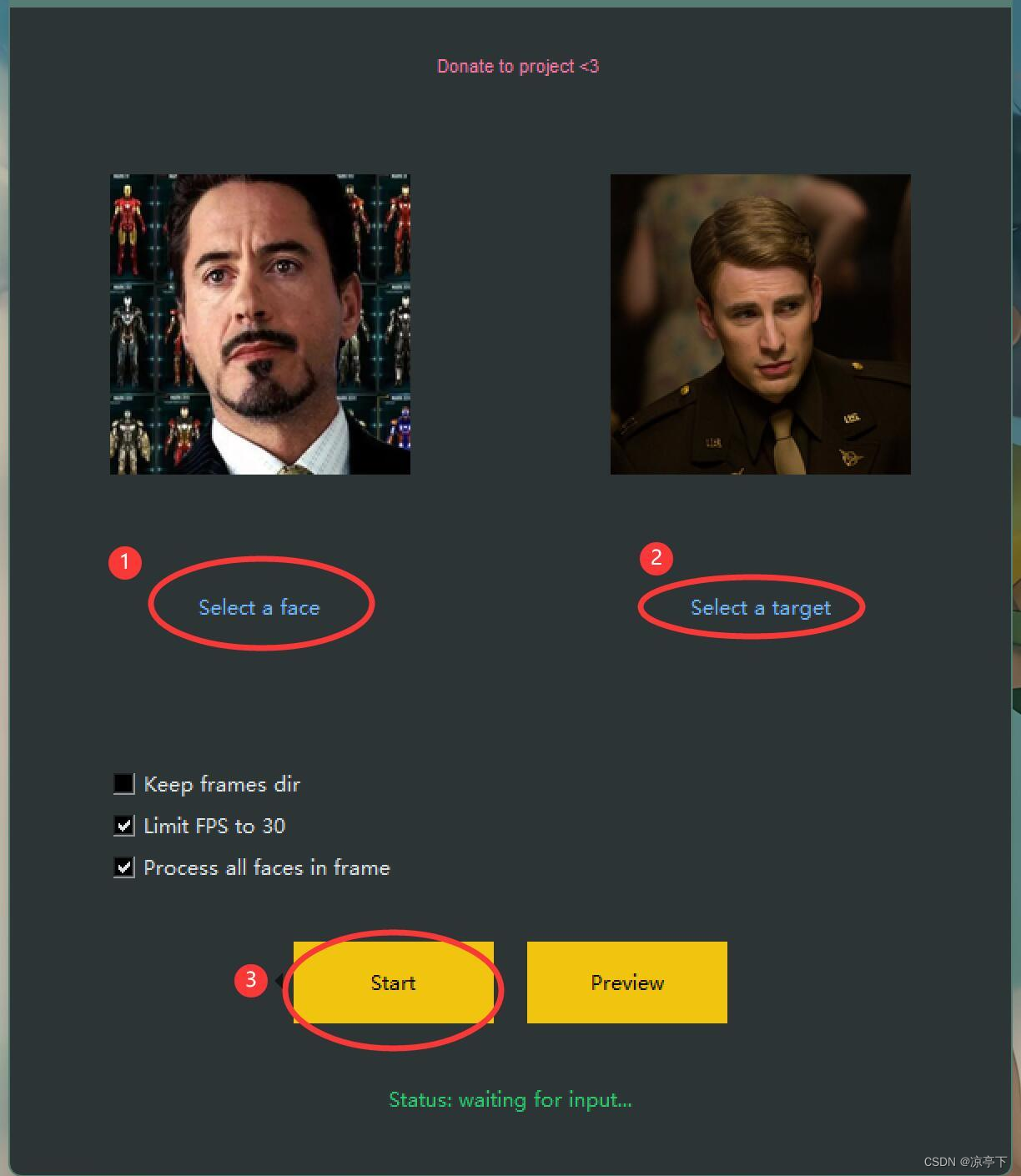
【AIGC】单图换脸离线版软件包及使用方法
云端再好,都不如放自己手里啊,想怎么就怎么玩。云端再好,都不如放自己手里啊,想怎么就怎么玩。 Roop作为一个新出的开源项目,配置起来还是有一定难度的。 我已经把各种依赖,模型,环境配置已经…...

8.19论文阅读
文章目录 Graph-Segmenter: Graph Transformer with Boundary-aware Attention for Semantic Segmentation方法 SCSC: Spatial Cross-scale Convolution Module to Strengthen both CNNs and Transformers方法 Deformable Mixer Transformer with Gating for Multi-Task Learni…...
HAProxy
目录 HAProxy HAProxy介绍 主要特性 LVS、nginx、HAProxy区别 nginx LVS HAProxy 负载均衡策略 Haproxy搭建 Web 群集 Haproxy服务器 编译安装 Haproxy Haproxy服务器配置 添加haproxy 系统服务 节点服务器部署 日志定义 HAProxy HAProxy介绍 HAProxy是可提供高…...

基于EasyExcel的Excel读取
1.引入依赖 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.2.11</version> </dependency>2.读取器代码: package com.vz.utils.excel;import com.alibaba.excel.Eas…...

链路聚合详解
链路聚合详解 华为交换机链路聚合:Linux链路聚合bond配置 华为交换机链路聚合: 方式一:配置手工负载分担方式的链路聚合 [CORE1] interface Eth-Trunk 1 [CORE1-Eth-Trunk1] trunkport GigabitEthernet 0/0/5 to 0/0/6 [CORE1-Eth-Trunk1] p…...

Shell编程学习之if分支语句的应用
Shell编程中的if分支语句:伪代码表示:注意符号和表达式之间的空格; if [ 表达式1 ] then分支1 elif [ 表达式2 ] then分支2 elif [ 表达式3 ] then分支3 else其它 fi按整型的方式,if分支语句比较字符串的大小:等于&am…...

2023.8 - java - 泛型
泛型问题的引出: jdk 1.5 引出泛型 // package 泛型; public class index {public static void main (String[] args){test t new test();t.setContent("aaa");int a (int) t.getContent();System.out.println(a);} }class test{Object content;publi…...

【数据结构练习】链表面试题锦集一
目录 前言: 1. 删除链表中所有值为key的节点 方法一:正常删除,头结点另外讨论 方法二:虚拟头结点法 方法三:递归 2.反转链表 方法一:双指针迭代 方法二:递归法解析: 3.链表的中间结点 方法…...
-[通用功能:SequentialChain和TransformationChain])
自然语言处理从入门到应用——LangChain:链(Chains)-[通用功能:SequentialChain和TransformationChain]
分类目录:《自然语言处理从入门到应用》总目录 SequentialChain 在调用语言模型之后,下一步是对语言模型进行一系列的调用。若可以将一个调用的输出作为另一个调用的输入时则特别有用。在本节中,我们将介绍如何使用顺序链来实现这一点。顺序…...

什么是卷积神经网络
目录 什么是卷积神经网络 全链接相对笨重:大胖子编辑 编辑 参数众多:容易造成过拟合 编辑 卷积核:进行图像特征提取,源于卷积原理:求相交面积 卷积的作用 卷积的意义 编辑 通过卷积核减少参数 深度卷积…...
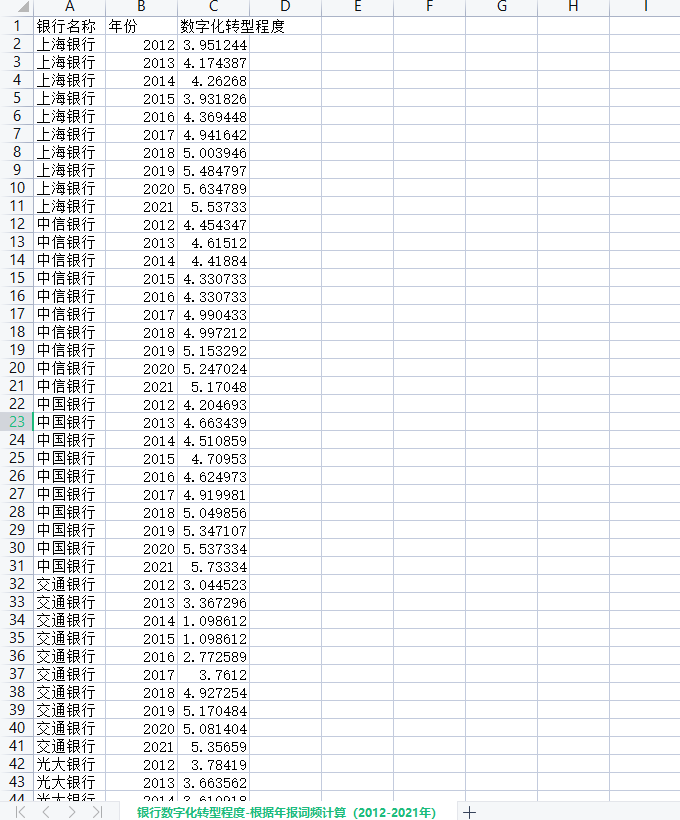
银行数字化转型程度-根据年报词频计算(2012-2021年)
银行数字化转型程度是根据银行年报中的数字化相关词频计算所得的数据。这一数据包括数字化词频关键词、以及数字化转型程度,反映了银行数字化转型的程度和进展情况。从经济学研究的角度来看,这一数据具有重要的参考价值。 首先,银行数字化转…...
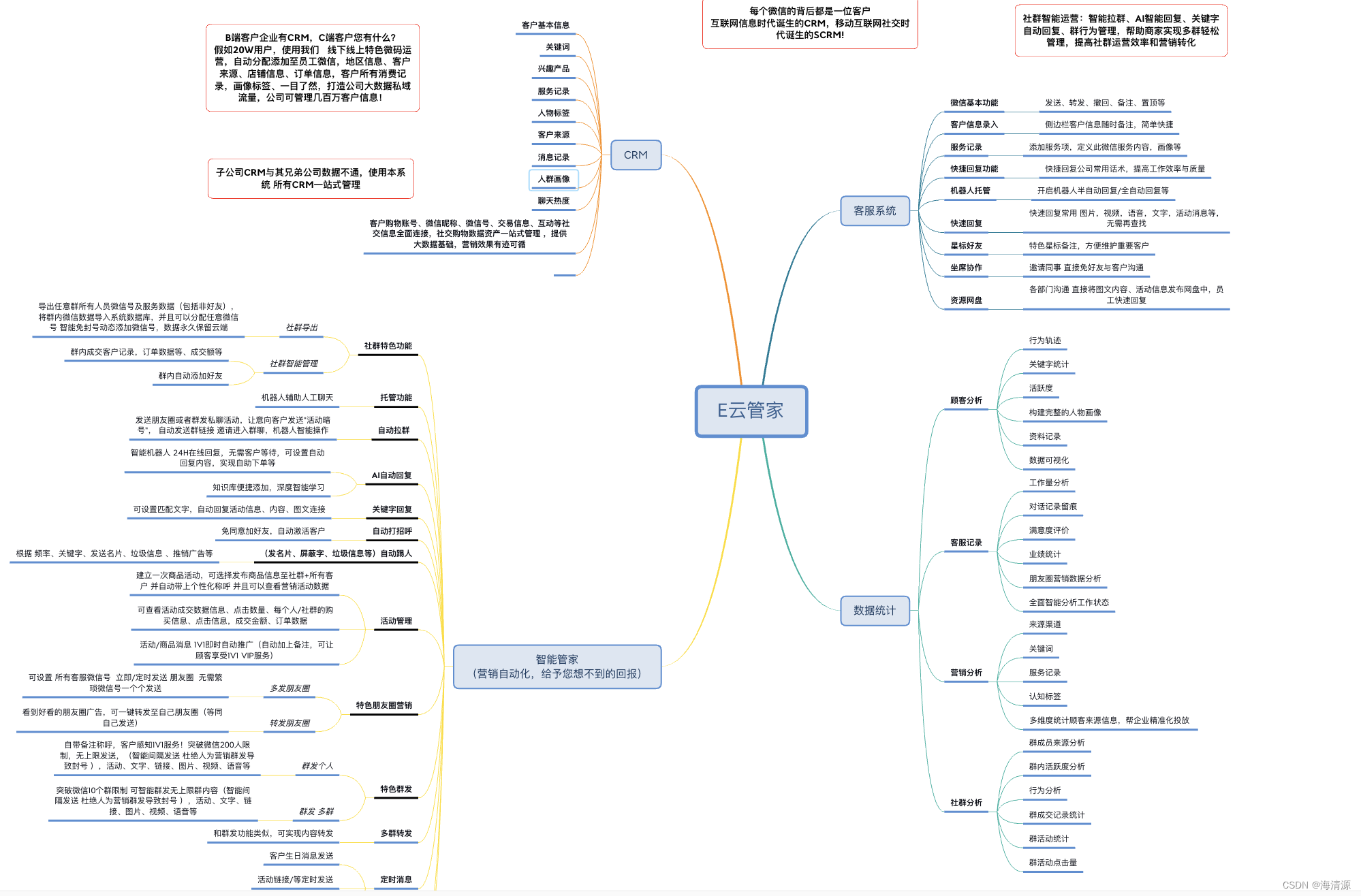
微信开发之一键修改群聊备注的技术实现
修改群备注 修改群名备注后,如看到群备注未更改,是手机缓存问题,可以连续点击进入其他群,在点击进入修改的群,再返回即可看到修改后的群备注名,群名称的备注仅自己可见 请求URL: http://域名地…...
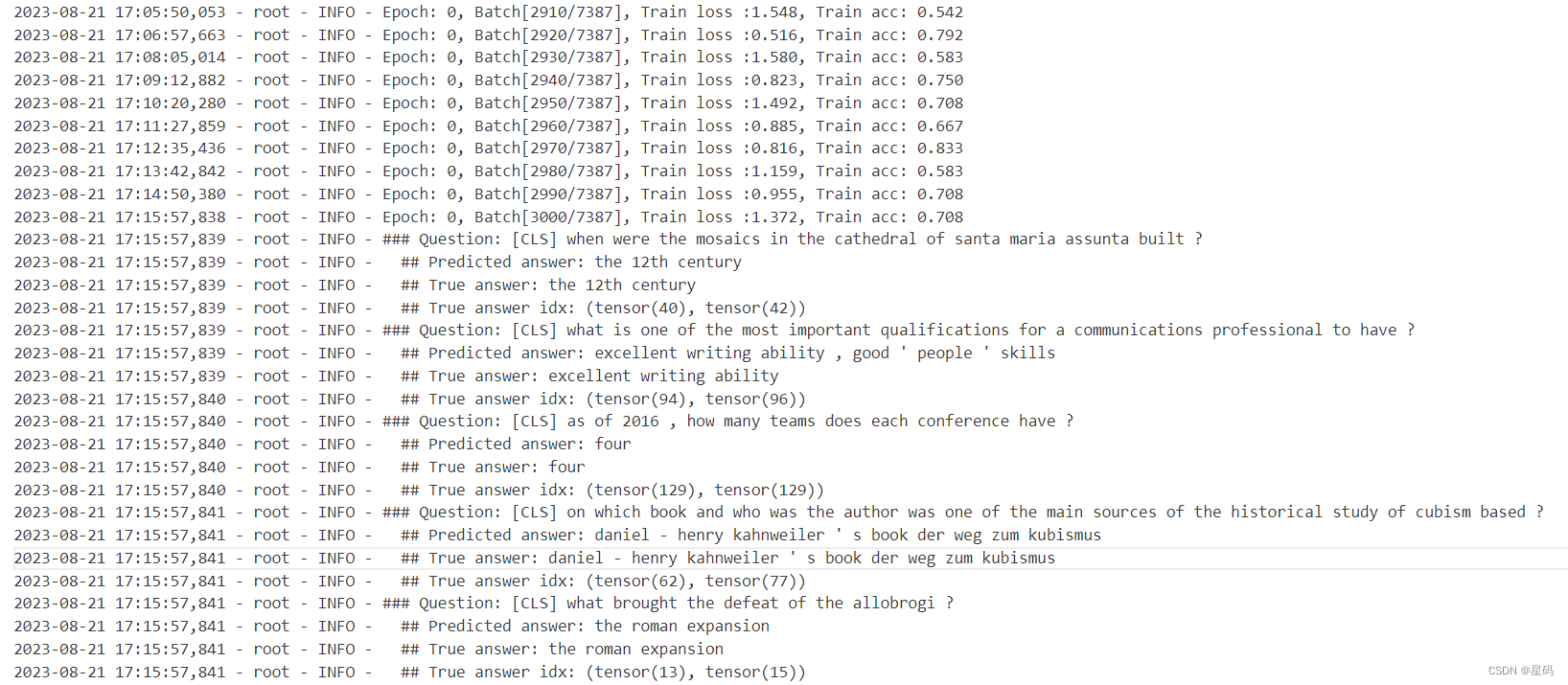
[oneAPI] 基于BERT预训练模型的SQuAD问答任务
[oneAPI] 基于BERT预训练模型的SQuAD问答任务 Intel Optimization for PyTorch and Intel DevCloud for oneAPI基于BERT预训练模型的SQuAD问答任务语料介绍数据下载构建 模型 结果参考资料 比赛:https://marketing.csdn.net/p/f3e44fbfe46c465f4d9d6c23e38e0517 Int…...
梯度下降法在强凸函数的收敛性分析)
机器学习笔记之优化算法(十七)梯度下降法在强凸函数的收敛性分析
机器学习笔记之优化算法——梯度下降法在强凸函数的收敛性分析 引言回顾:梯度下降法在强凸函数的收敛性二阶可微——梯度下降法在强凸函数的收敛性推论 引言 上一节介绍并证明了:梯度下降法在强凸函数上的收敛速度满足 Q \mathcal Q Q-线性收敛。 本节将…...
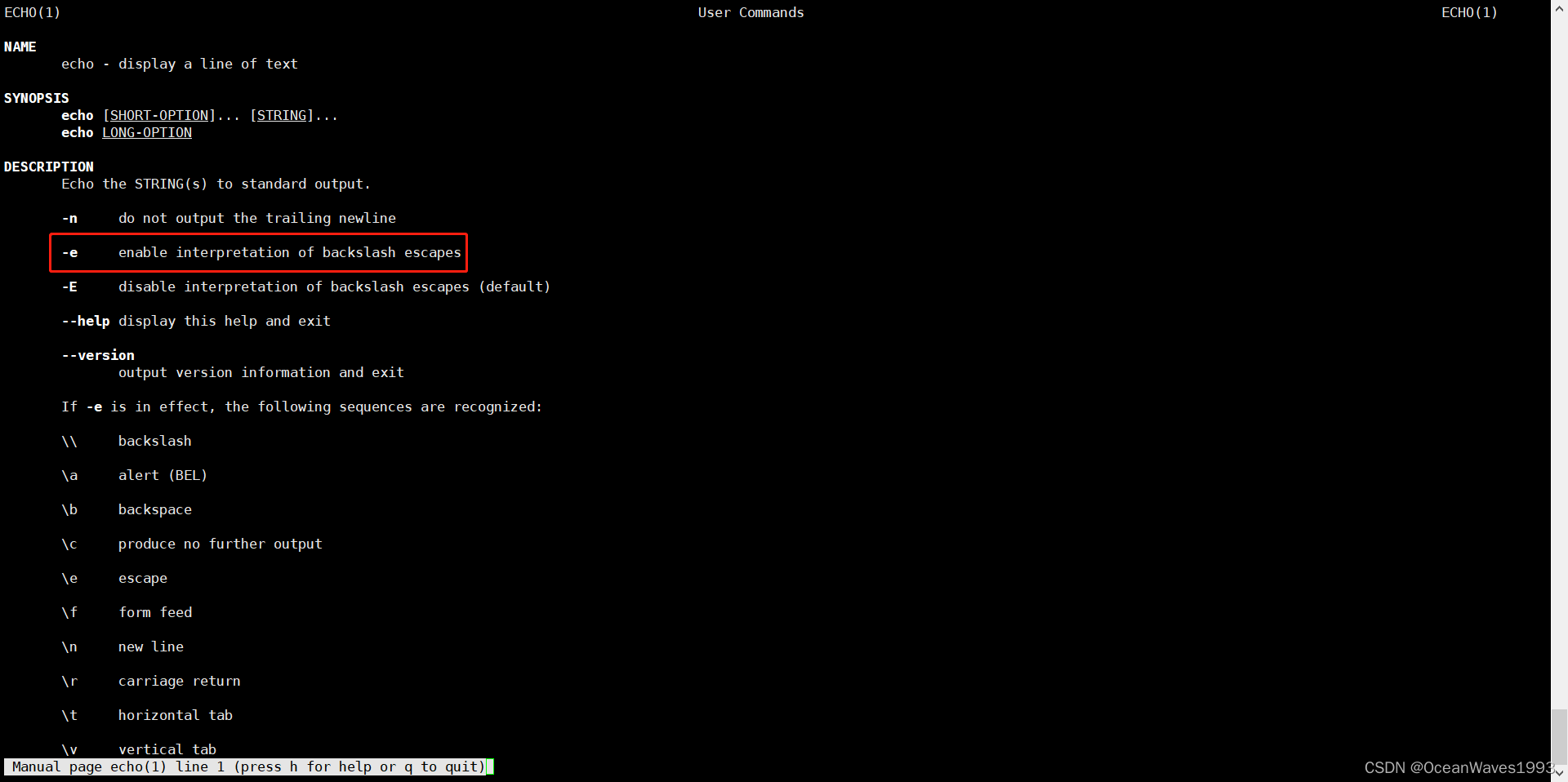
shell脚本中linux命令的特殊用法记录
shell脚本中linux命令的特殊用法记录 1、linux命令特殊参数选项1.1、sed -e1.2、echo -e 2、 shell 扩展2.1、[[ ]]支持用~进行正则匹配 3、特殊命令用法3.1、{} 变量替换 1、linux命令特殊参数选项 1.1、sed -e sed -e以严格模式执行脚本,在sed -e 后面的所有命令…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
