微信开发之一键修改群聊备注的技术实现
修改群备注
修改群名备注后,如看到群备注未更改,是手机缓存问题,可以连续点击进入其他群,在点击进入修改的群,再返回即可看到修改后的群备注名,群名称的备注仅自己可见
请求URL:
http://域名地址/modifyGroupRemark
请求方式:
- POST
请求头Headers:
- Content-Type:application/json
- Authorization:login接口返回
参数:
| 参数名 | 必选 | 类型 | 说明 |
|---|---|---|---|
| wId | 是 | String | 登录实例标识 |
| chatRoomId | 是 | String | 群号 |
| content | 是 | String | 群名 |
请求参数示例
{"wId": "349be9b5-8734-45ce-811d-4e10ca568c67","chatRoomId":"24187765053@chatroom","content":"我爱你中国啊啊啊啊啊"
}成功返回示例
{"message": "成功","code": "1000","data": null
}错误返回示例
{"message": "失败","code": "1001","data": null
}返回数据:
| 参数名 | 类型 | 说明 |
|---|---|---|
| code | String | 1000成功 1001失败 |
| msg | String | 反馈信息 |
| data | JSONObject |
测试地址:https://wkteam.cn/
相关文章:

微信开发之一键修改群聊备注的技术实现
修改群备注 修改群名备注后,如看到群备注未更改,是手机缓存问题,可以连续点击进入其他群,在点击进入修改的群,再返回即可看到修改后的群备注名,群名称的备注仅自己可见 请求URL: http://域名地…...
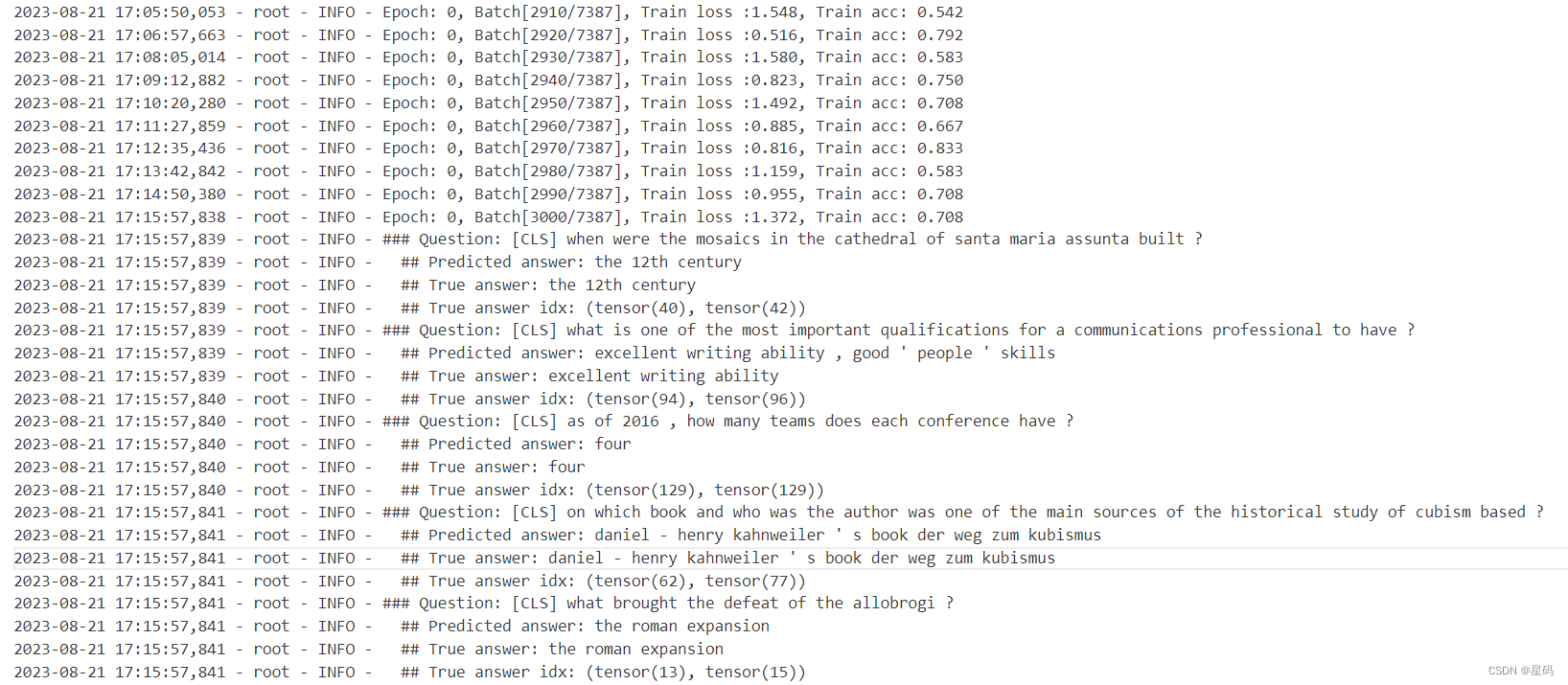
[oneAPI] 基于BERT预训练模型的SQuAD问答任务
[oneAPI] 基于BERT预训练模型的SQuAD问答任务 Intel Optimization for PyTorch and Intel DevCloud for oneAPI基于BERT预训练模型的SQuAD问答任务语料介绍数据下载构建 模型 结果参考资料 比赛:https://marketing.csdn.net/p/f3e44fbfe46c465f4d9d6c23e38e0517 Int…...
梯度下降法在强凸函数的收敛性分析)
机器学习笔记之优化算法(十七)梯度下降法在强凸函数的收敛性分析
机器学习笔记之优化算法——梯度下降法在强凸函数的收敛性分析 引言回顾:梯度下降法在强凸函数的收敛性二阶可微——梯度下降法在强凸函数的收敛性推论 引言 上一节介绍并证明了:梯度下降法在强凸函数上的收敛速度满足 Q \mathcal Q Q-线性收敛。 本节将…...
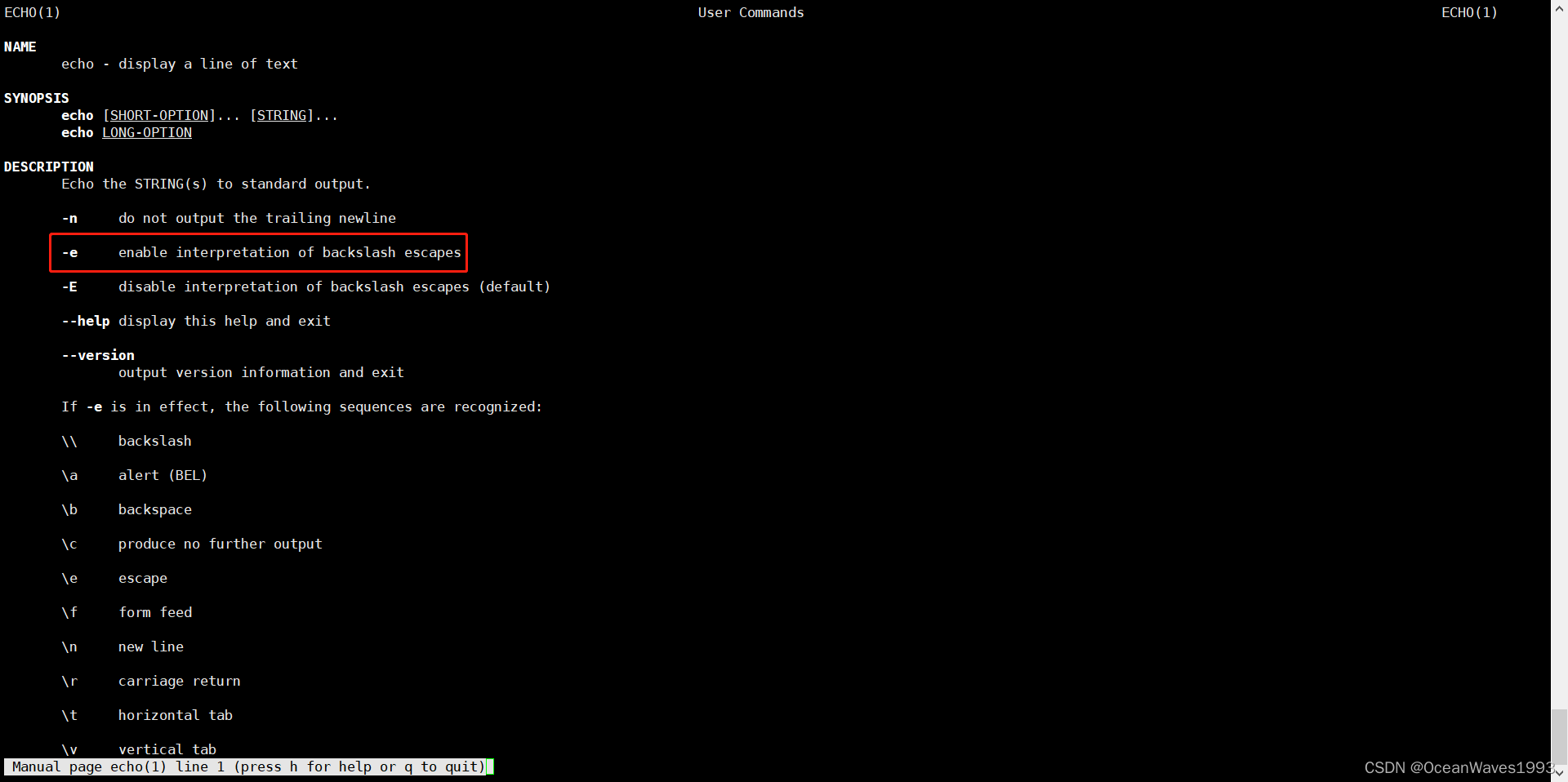
shell脚本中linux命令的特殊用法记录
shell脚本中linux命令的特殊用法记录 1、linux命令特殊参数选项1.1、sed -e1.2、echo -e 2、 shell 扩展2.1、[[ ]]支持用~进行正则匹配 3、特殊命令用法3.1、{} 变量替换 1、linux命令特殊参数选项 1.1、sed -e sed -e以严格模式执行脚本,在sed -e 后面的所有命令…...

Nvidia H100:今年55万张够用吗?
原文标题:Nvidia H100: Are 550,000 GPUs Enough for This Year? 作者:Doug Eadline August 17, 2023 The GPU Squeeze continues to place a premium on Nvidia H100 GPUs. In a recent Financial Times article, Nvidia reports that it expects to…...
)
【Vue2.0源码学习】生命周期篇-初始化阶段(initLifecycle)
文章目录 1. 前言2. initLifecycle函数分析3. 总结 1. 前言 在上篇文章中,我们介绍了生命周期初始化阶段的整体工作流程,以及在该阶段都做了哪些事情。我们知道了,在该阶段会调用一些初始化函数,对Vue实例的属性、数据等进行初始…...
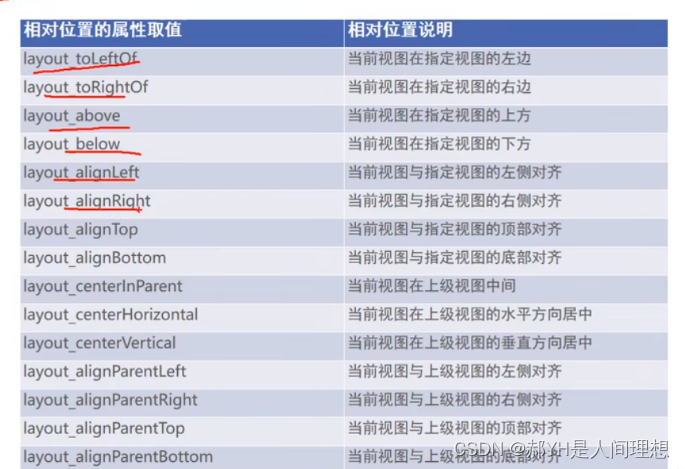
Android开发基础知识总结(三)简单控件(上)
一.文本显示 考虑到结构样式相分离的思想,我们往往在XML中设置文本 <TextViewandroid:layout_width"342dp"android:layout_height"70dp"android:text"房价计算器"android:layout_gravity"center"android:textColor"…...
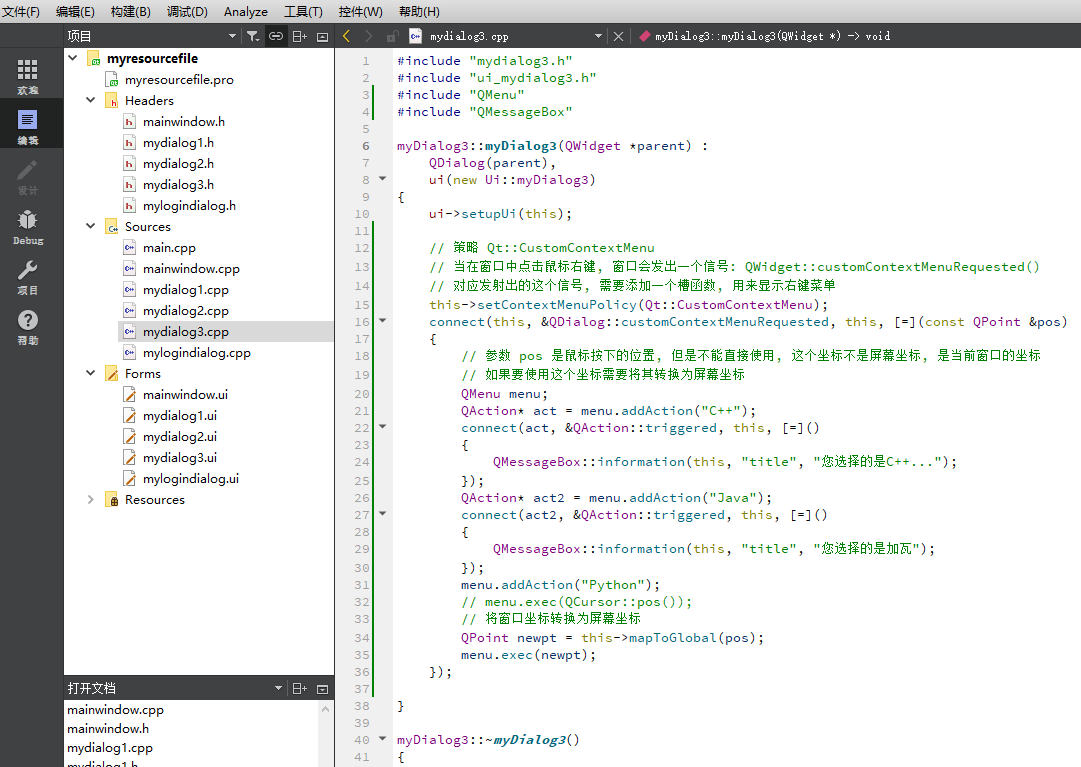
在Qt窗口中添加右键菜单
在Qt窗口中添加右键菜单 基于鼠标的事件实现流程demo 基于窗口的菜单策略实现Qt::DefaultContextMenuQt::ActionsContextMenuQt::CustomContextMenu信号API 基于鼠标的事件实现 流程 需要使用:事件处理器函数(回调函数) 在当前窗口类中重写鼠标操作相关的的事件处理器函数&a…...

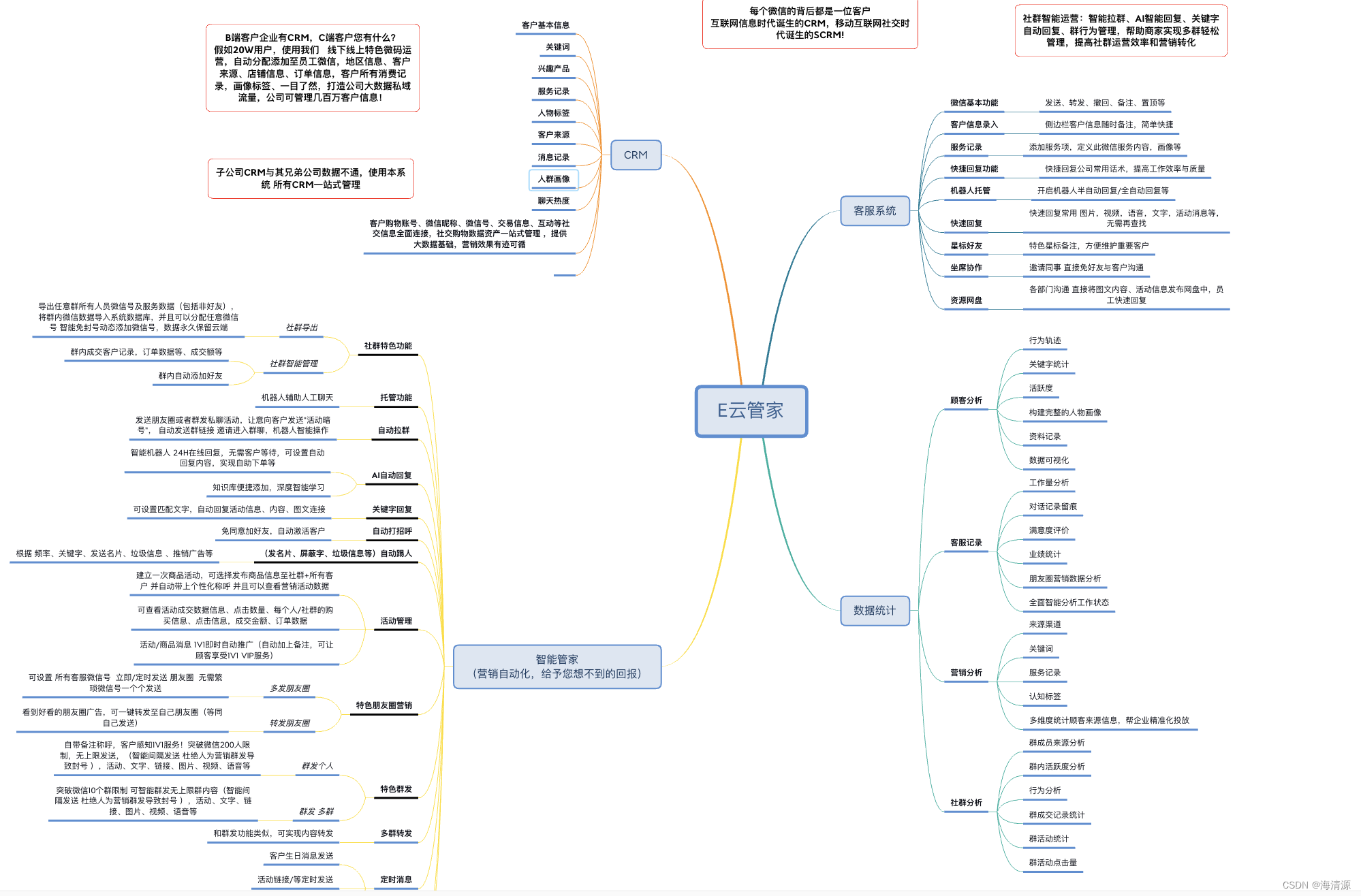
Day8 智慧商城
项目演示 项目收获 创建项目 调整初始化目录 1.删components里的所有文件 2.删views里的所有文件 3.router/index.js 删路由 删规则 import Vue from vue import VueRouter from vue-routerVue.use(VueRouter)const router new VueRouter({routes: [] })export default route…...

LeetCode:Hot100python版本之回溯
回溯算法其实是纯暴力搜索。for循环嵌套是写不出的 组合:没有顺序 排列:有顺序 回溯法可以抽象为树形结构。只有在回溯算法中递归才会有返回值。 46. 全排列 排列是有顺序的。 组合类问题用startindex,排序类问题用used,来标…...
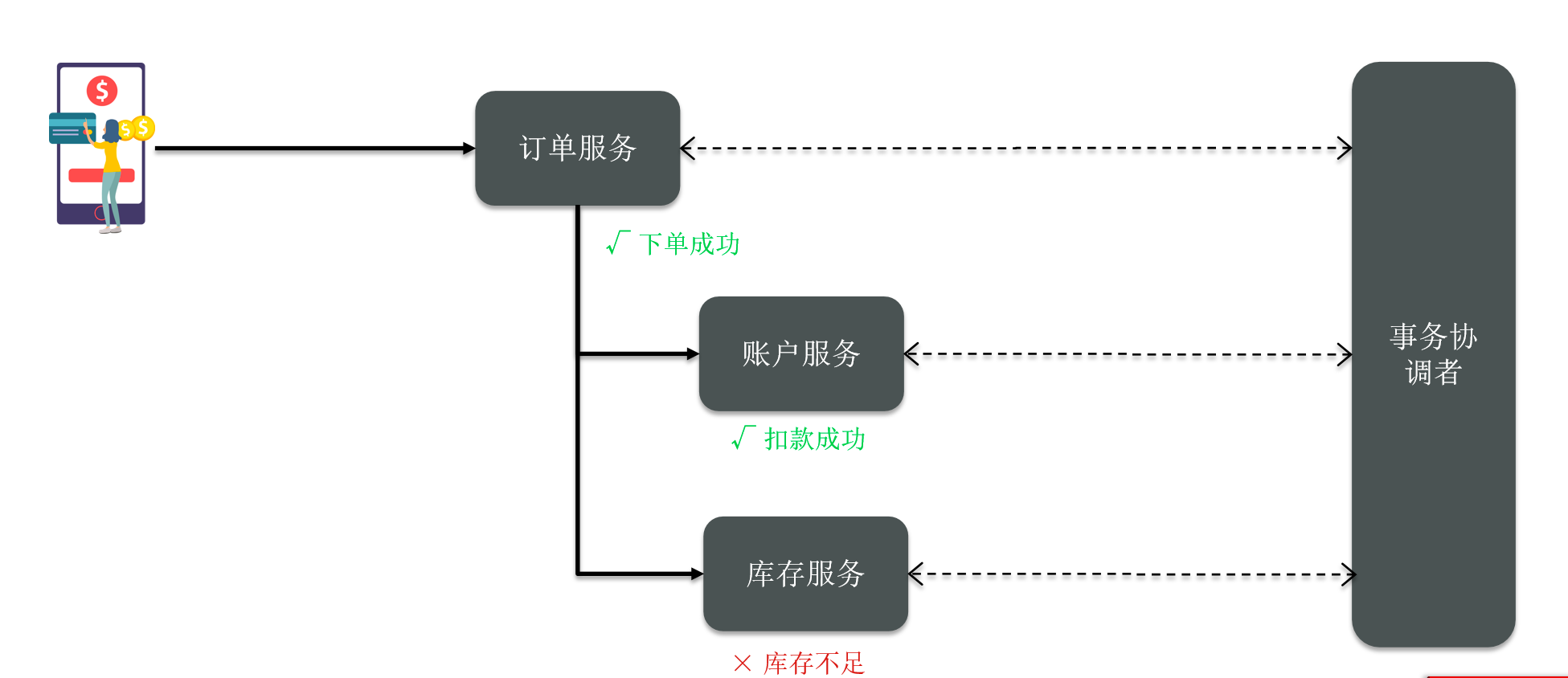
分布式事务理论基础
今天啊,本片博客我们一起来学习一下微服务中的一个重点和难点知识:分布式事务。 我们会基于Seata 这个框架来学习。 1、分布式事务问题 事务,我们应该比较了解,我们知道所有的事务,都必须要满足ACID的原则。也就是 …...

线性代数强化第三章
目录 一,关于A伴随,A逆与初等矩阵 二,分块矩阵 三,矩阵方程 一,关于A伴随,A逆与初等矩阵 如何证明行列式的值不能是0; 此秩为1. 法一: 法二: 不用看是列变换还是行变…...
---之配置)
搭建自己的私有 开源LoRaWAN 网络服务器(The ThingsStack)---之配置
介绍 这是使用 Docker 在您自己的硬件上安装 Things Stack Enterprise 或开源代码以运行您自己的私有 LoRaWAN 网络服务器的指南。 运行 The Things Stack 的方法有多种。 Things Stack 开源和企业发行版旨在在您自己的硬件上运行,本指南也对此进行了介绍。 对于具有高吞吐量的…...
多维时序 | MATLAB实现SCNGO-CNN-Attention多变量时间序列预测
多维时序 | MATLAB实现SCNGO-CNN-Attention多变量时间序列预测 目录 多维时序 | MATLAB实现SCNGO-CNN-Attention多变量时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.SCNGO-CNN-Attention超前24步多变量回归预测算法。 程序平台:无Attention适…...

clickhouse的删除和更新
clickhouse不擅长更新和删除操作,更新操作很重,更新是重新创建一个分区,更新完后,太混之前的 ClickHouse提供了DELETE和UPDATE的能力,这类操作被称为Mutation查询,它可以看作ALTER语句的变种。虽然Mutation…...
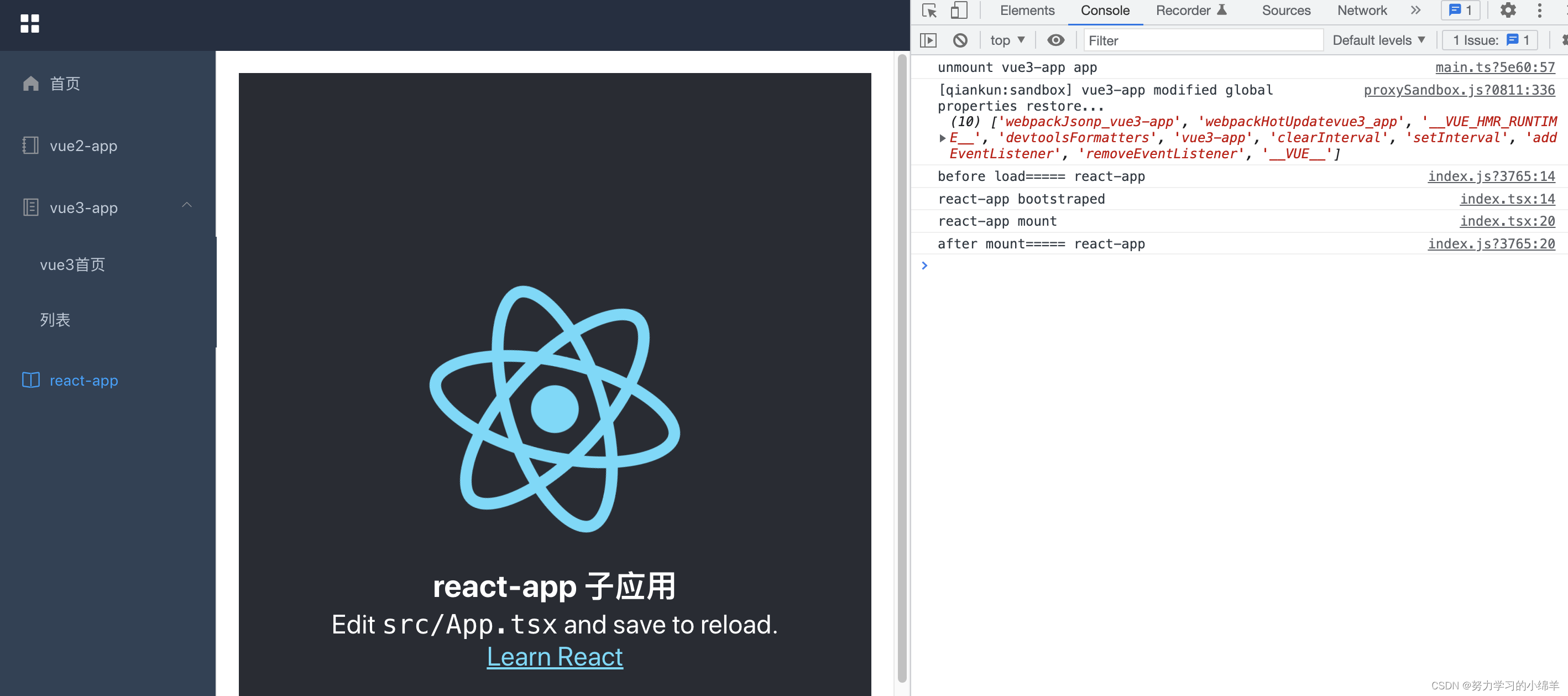
微前端 - qiankun
qiankun 是一个基于 single-spa 的微前端实现库,旨在帮助大家能更简单、无痛的构建一个生产可用微前端架构系统。 本文主要记录下如何接入 qiankun 微前端。主应用使用 vue2,子应用使用 vue3、react。 一、主应用 主应用不限技术栈,只需要提…...

前端编辑页面修改后和原始数据比较差异
在软件研发过程中,会遇到很多编辑页面,有时编辑页面和新增页面长的基本上一样,甚至就是一套页面供新增和编辑共用。编辑页面的场景比较多,例如: 场景一、字段比较多,但实际只修改了几个字段,如…...

docker第一次作业
docker第一次作业 1.安装docker服务,配置镜像加速器 yum install -y yum-utils device-mapper-persistent-data lvm2 yum-config-manager --add-repo https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo sed -i sdownload.docker.commirrors.aliy…...

Springboot3.0.0+集成SpringDoc并配置knife4j的UI
环境:JDK17,Springboot3,springdoc2,knife4j 4 Springdoc本身也是集成了Swagger3,而knife4j美化了Swagger3的UI Knife4j官网: 快速开始 | Knife4j Springdoc官网 OpenAPI 3 Library for spring-boot 1.pom配置 由于此knife4j内依赖了S…...
电脑运行缓慢?4个方法,加速电脑运行!
“我电脑才用了没多久哎!怎么突然就变得运行很缓慢了呢?有什么方法可以加速电脑运行速度吗?真的很需要,看看我吧!” 电脑的运行速度快会让用户在使用电脑时感觉愉悦,而电脑运行缓慢可能会影响我们的工作效率…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
