【C++】AVLTree——高度平衡二叉搜索树
文章目录
- 一、AVL树的概念
- 二、AVL树节点的定义
- 三、AVL树的插入
- 四、AVL树的旋转
- 1.左单旋
- 2.右单旋
- 3.左右双旋
- 4.右左双旋
- 五、进行验证
- 六、AVLTree的性能
个人简介📝
🏆2022年度博客之星Top18;🏆2022社区之星Top2;的🥇C/C++领域优质创作者;
🥇阿里云专家博主;🥇华为云云享专家;🥇腾讯云年度进取作者;🥇掘金成长之星;
一、AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
平衡因子= 右子树高度-左子树高度
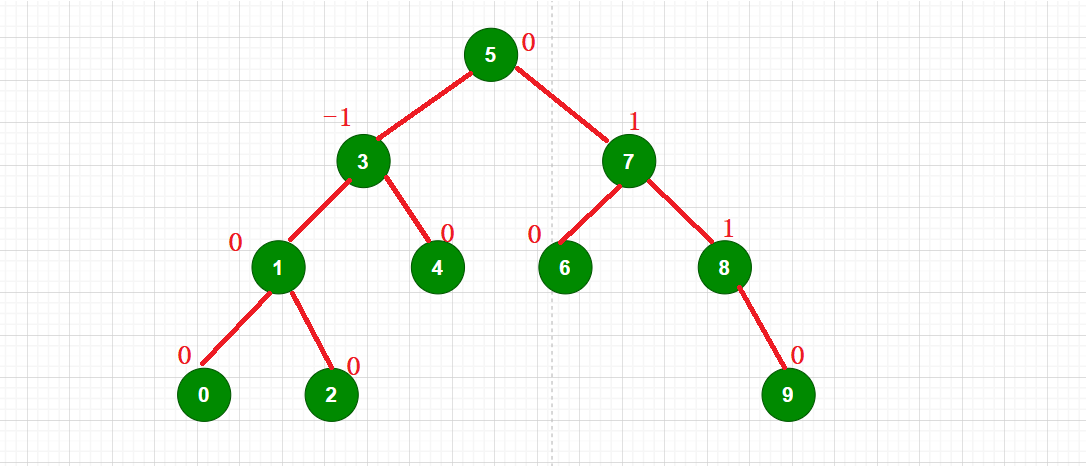
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log2N) ,搜索时间复杂度O(log2N)
二、AVL树节点的定义
节点结构:三叉链结构(左、右、父),以及平衡因子bf+构造函数(左右为空,平衡因子初始化为0)
template<class K,class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//balance factorAVLTreeNode(const pair<K,V>&kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
三、AVL树的插入
AVL树在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。步骤过程:
找到插入的位置:根据二叉搜索树的做法
进行插入:判断插入的位置是parent的左还是右
更新平衡因子:如果不平衡的话,就要进行
旋转
找到插入位置(比较节点大小即可):
- 插入的节点key值
>当前位置的key值,往右子树走 - 插入的节点key值
<当前位置的key值,往左子树走 - 插入的节点key值等于当前位置的key值,不能插入,返回false
插入之后,与二叉搜索树不同的是:我们还需要去进行平衡因子的更新,调平衡:
如果新增加的在右,平衡因子加加
如果新增加的在左,平衡因子减减
更新一个结点之后我们需要去进行判断,子树的高度是否发生了变化:
1.如果parent的平衡因子是0:说明之前parent的平衡因子是1或-1,说明之前parent一边高、一边低;这次插入之后填入矮的那边,parent所在的子树高度不变,不需要继续往上更新
2.如果parent的平衡因子是1或者-1:说明之前parent的平衡因子是0,两边一样高,插入之后一边更高,parent所在的子树高度发生变化,继续往上更新
3.平衡因子是2或-2,说明之前parent的平衡因子是1或-1,现在插入严重不平衡,违反规则,需要进行旋转处理
最坏的情况下:需要一直更新到根root:
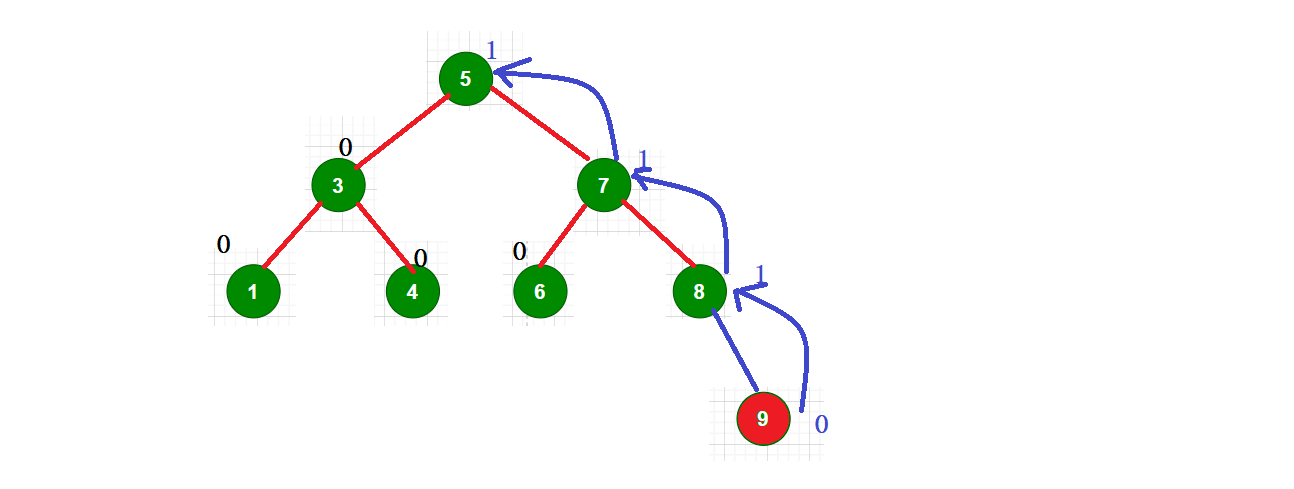
我们更新平衡因子时第一个更新的就是parent,如果parent->_bf1或parent->_bf-1需要继续往上进行平衡因子的更新,向上迭代,直到parent为空的情况:
else if (parent->_bf == 1 || parent->_bf == -1)
{cur = parent;parent = parent->_parent;
}
当parent->_bf = 2或parent->_bf==-2时,我们就需要进行旋转了:
🔴如果parent的平衡因子是2,cur的平衡因子是1时,说明右边的右边比较高,我们需要进行左单旋
🔴如果parent的平衡因子是-2,cur的平衡因子是-1时,说明左边的左边比较高,我们需要进行右单旋
🔴如果parent的平衡因子是-2,cur的平衡因子是1时,我们需要进行左右双旋
🔴如果parent的平衡因子是2,cur的平衡因子是-1时,我们需要进行右左双旋
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//更新平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if(parent->_bf==2||parent->_bf==-2){//左旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右旋else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//左右双旋else if (parent-> _bf == -2&&cur->_bf==1){RotateLR(parent);}//右左双旋else if (parent->_bf ==2&&cur->_bf ==-1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;}
四、AVL树的旋转
在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种。
旋转规则:
1.让这颗子树左右高度差不超过1
2.旋转过程中继续保持它是搜索树
3.更新调整孩子节点的平衡因子
4.让这颗子树的高度根插入前保持一致
1.左单旋
新节点插入较高右子树的右侧—右右:左单旋
抽象图:
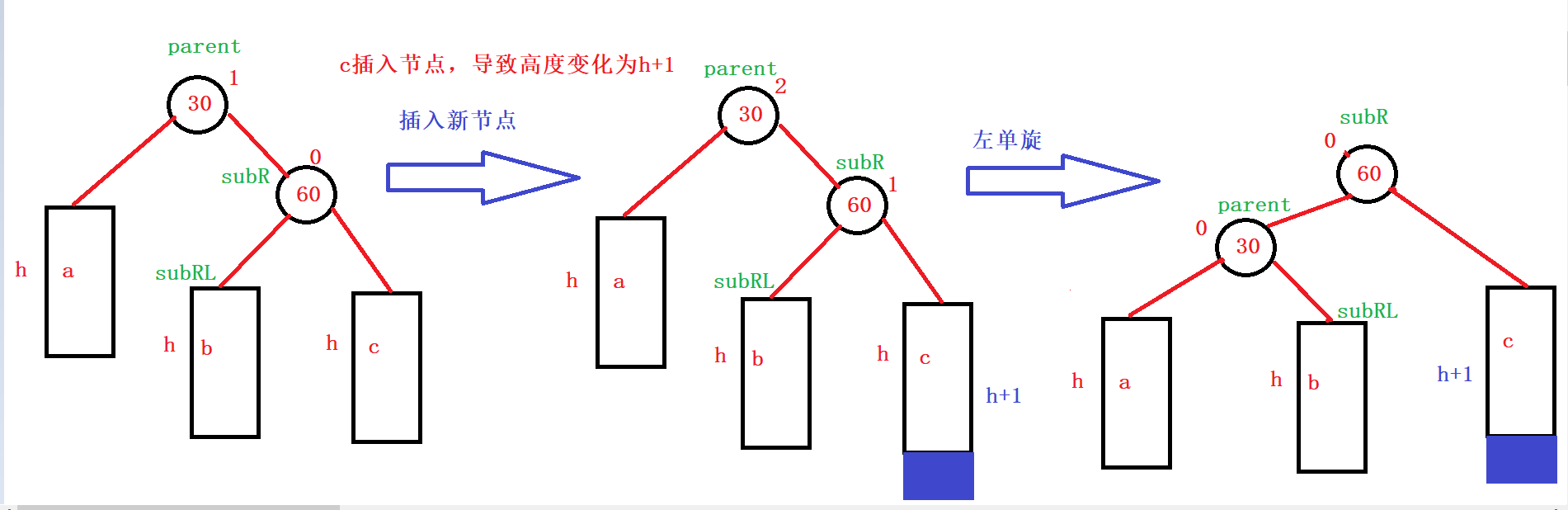
a/b/c是高度为h的AVL子树,代表多数情况:h>=0,其中h可以等于0、1、2…,不过都可以抽象成h,处理情况都一样:此时parent等于2,subR等于1。
具体左旋的步骤:
subRL成为parent的右子树:注意
subL和parent的关系,调整parent的右以及subRL的父(subRL可能为空)parent成为subR的左子树:调整parent的父与subR的左
subR成为相对的根节点:调整subR与ppNode:注意parent是不是整棵树的root,如果是,则让subR为_root,同时让_root->_parent置为空
更新平衡因子
左旋调整:subR的左子树值(subRL)本身就比parent的值要大,所以可以作为parent的右子树;而parent及其左子树当中结点的值本身就比subR的值小,所以可以作为subR的左子树。
**更新平衡因子bf:**subR与parent的bf都更新为0
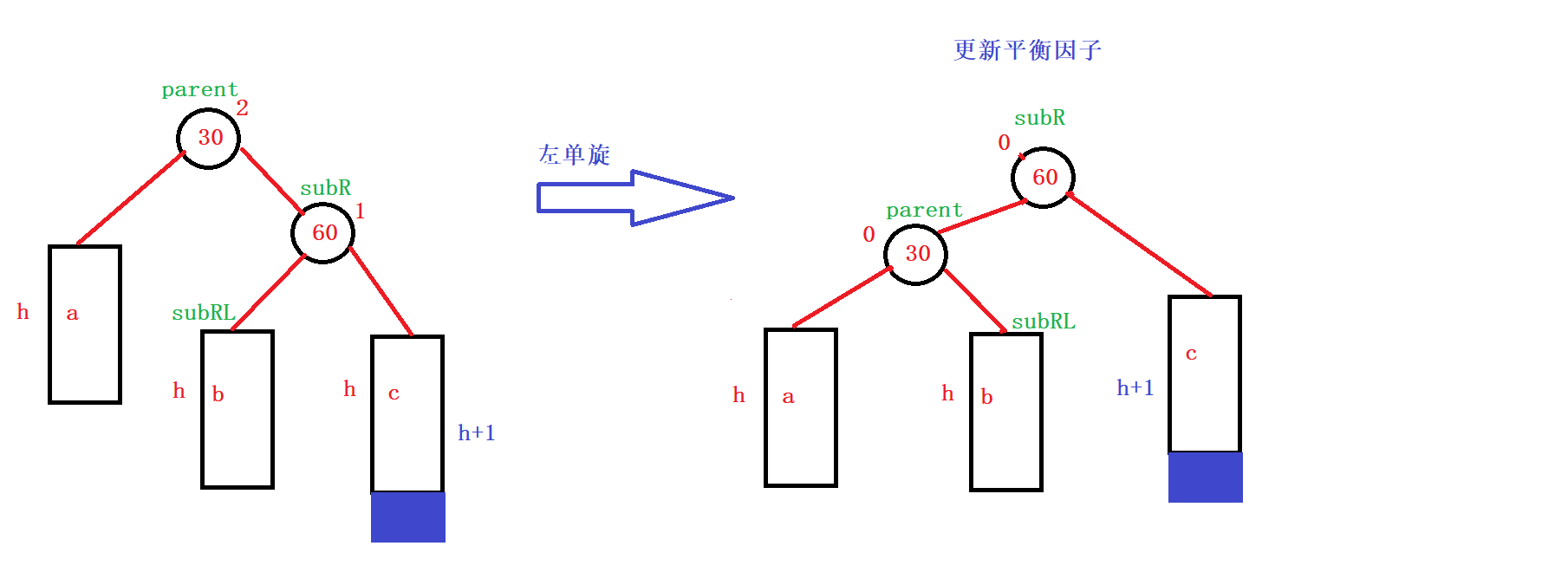
代码实现左旋转:
//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}parent->_bf = subR->_bf = 0;}
2.右单旋
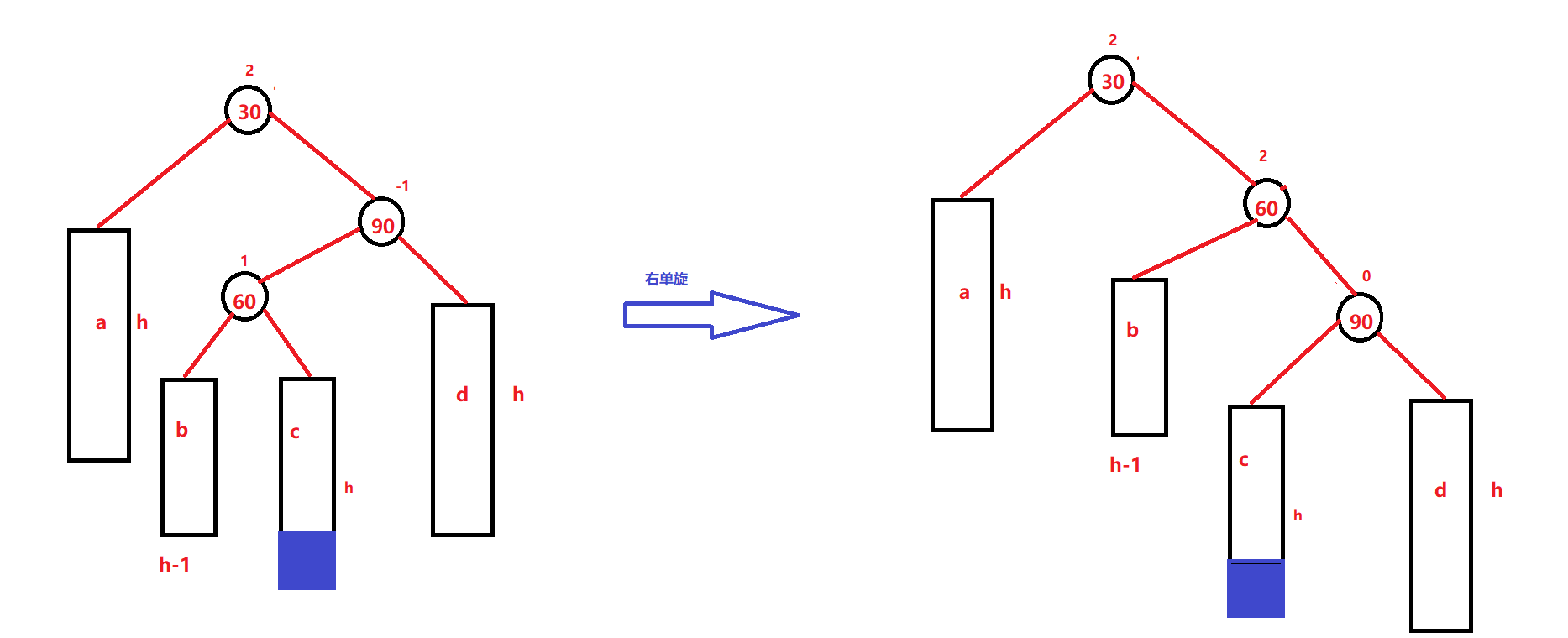
新节点插入较高左子树的左侧—左左:右单旋
有了前面左旋的基础,我们在来看右旋就没有那么费劲了:
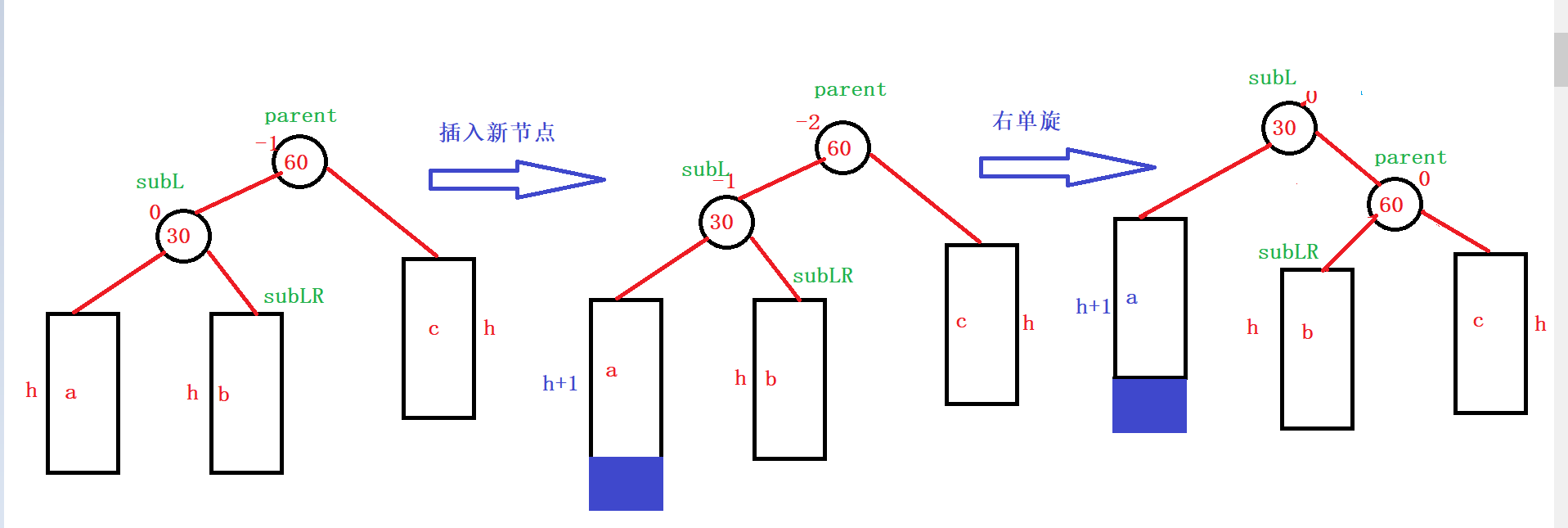
a/b/c是高度为h的AVL树,右旋旋转动作:b变成60的左边,60变成30的右边,30变成子树的根。
30比60小,b值是处于30和60之间,此时作为60的左边是没有问题的。
有了这个图,在结合前面左单旋的基础,我们就能很快实现我们的右单旋代码:
//右单旋
void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subL;subL->_right = parent;//if(_root==parent)if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;}
3.左右双旋
新节点插入较高左子树的右侧—左右:先左单旋再右单旋
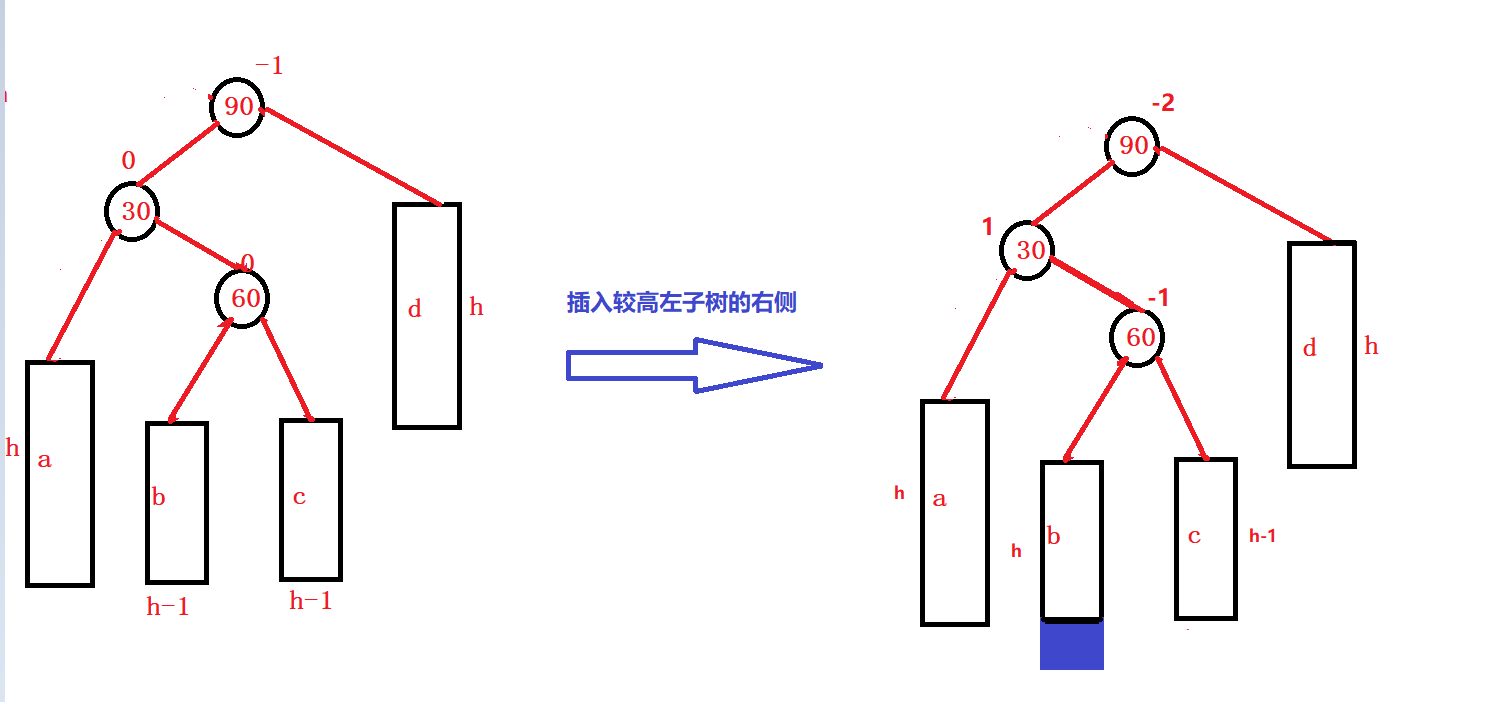
a/d是高度为h的AVL树,b/c是高度为h-1的AVL树。
以30为轴点进行左单旋:b变成30的右边,30变成60的左边,60变成子树根
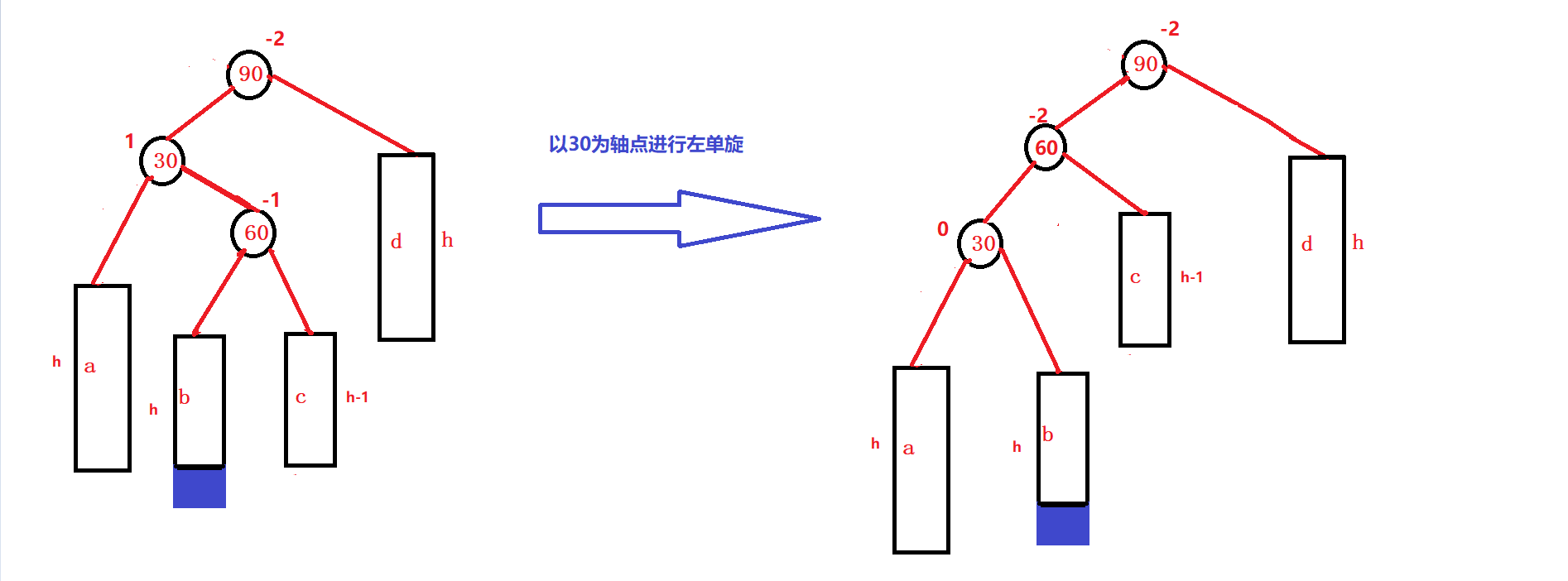
以90为轴点进行右单旋:c变成90的左边,90变成60的右边,60变成子树的根
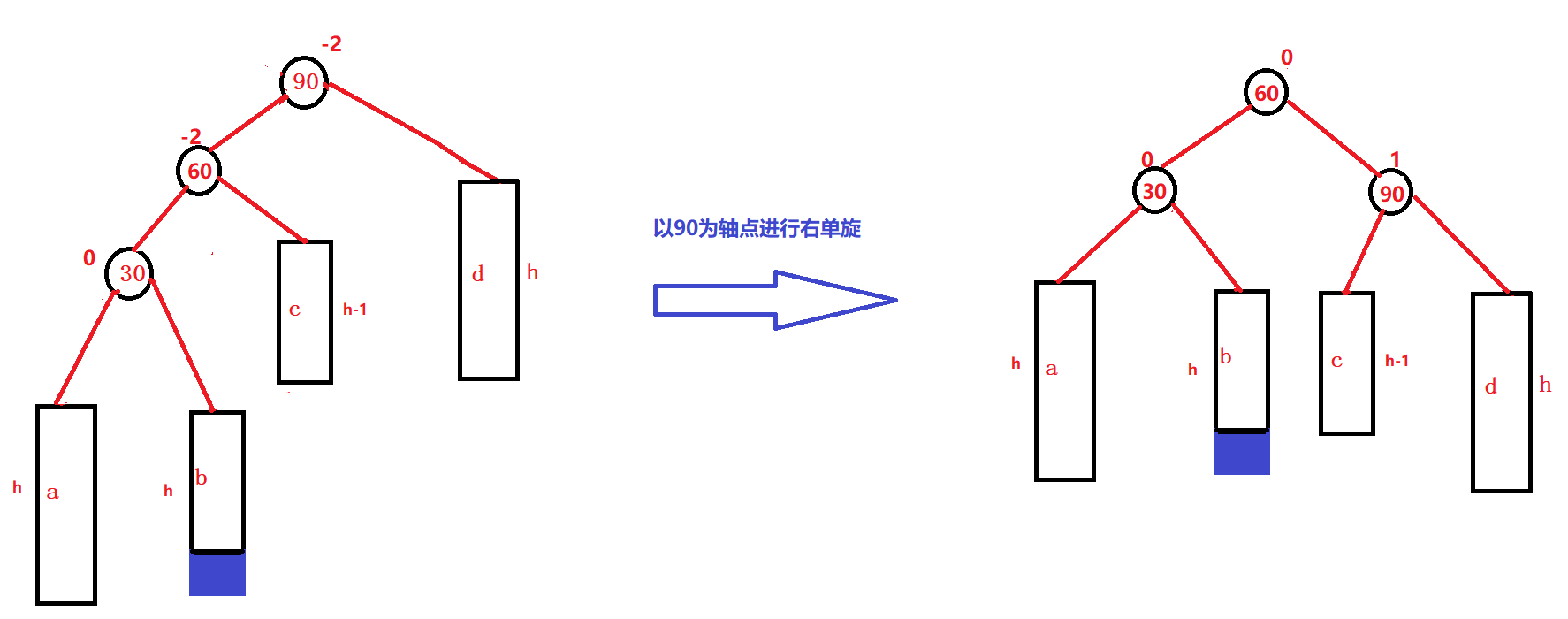
左右双旋:以subL为轴点左旋,以parent为轴点进行右旋,在进行平衡因子的更新(最大的问题)
我们从总体的角度来看,左右双旋的结果就是:就是把subLR的左子树和右子树,分别作为subL和parent的右子树和左子树,同时subL和parent分别作为subLR的左右子树,最后让subLR作为整个子树的根
subLR的左子树作为subL的右子树:因为subLR的左子树结点比subL的大
subLR的右子树作为parent的左子树:因为subLR的右子树结点比parent的小
平衡因子的更新:重新判断(识别插入节点是在b还是在c)根据subLR平衡因子的初始情况进行分类:
- 如果subLR初始平衡因子是-1时,左右双旋后parent、subL、subLR的平衡因子分别更新为1、0、0(插入在b)
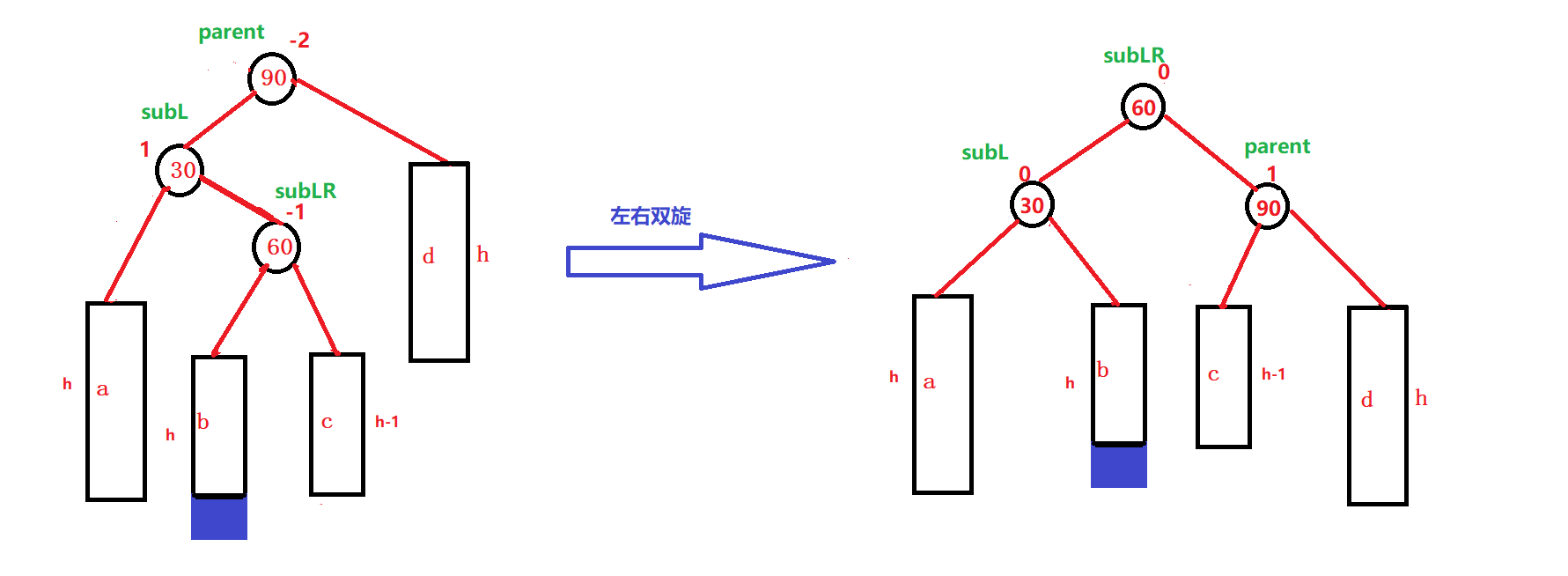
- 如果subLR的初始平衡因子是1时,左右双旋后parent、subL、subLR的平衡因子分别更新为0、-1、0(插入在c)
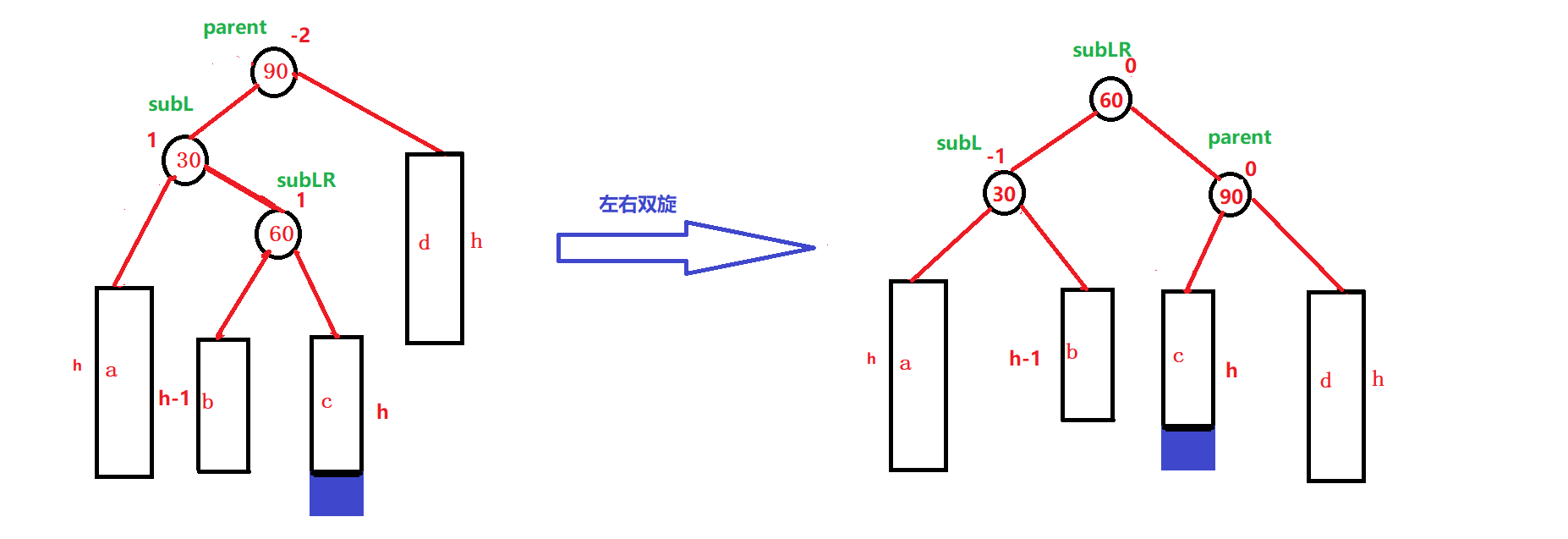
- 如果subLR初始平衡因子是0时,左右双旋后parent、subL、subLR的平衡因子分别更新为0、0、0(subLR自己新增)
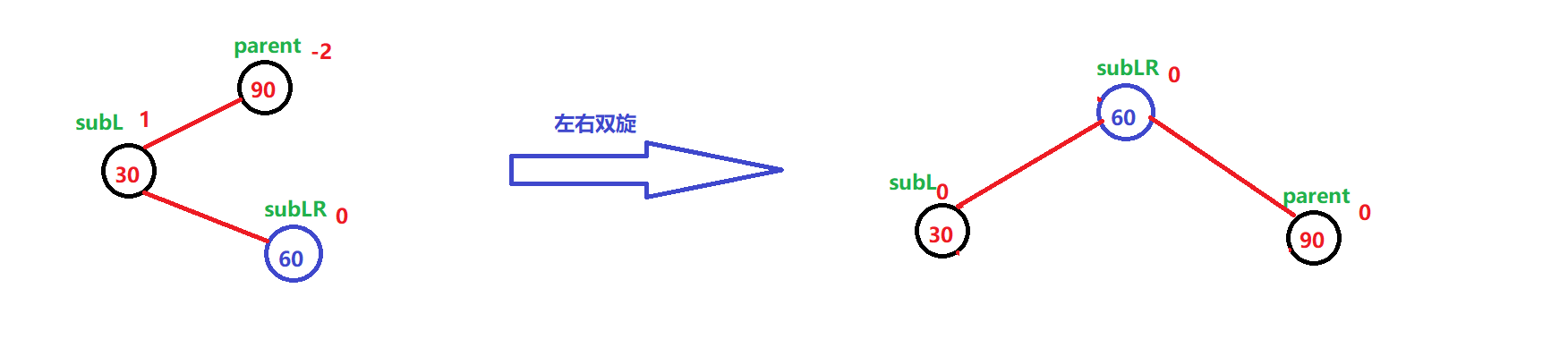
代码实现:
//左右双旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR ->_bf;RotateL(parent->_left);RotateR(parent);//更新平衡因子if (bf == -1)//b插入,subLR左子树新增{subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1)//c插入,subLR右子树新增{parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == 0)//subLR自己新增加{parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}
4.右左双旋
新节点插入较高右子树的左侧—右左:先右单旋再左单旋
插入
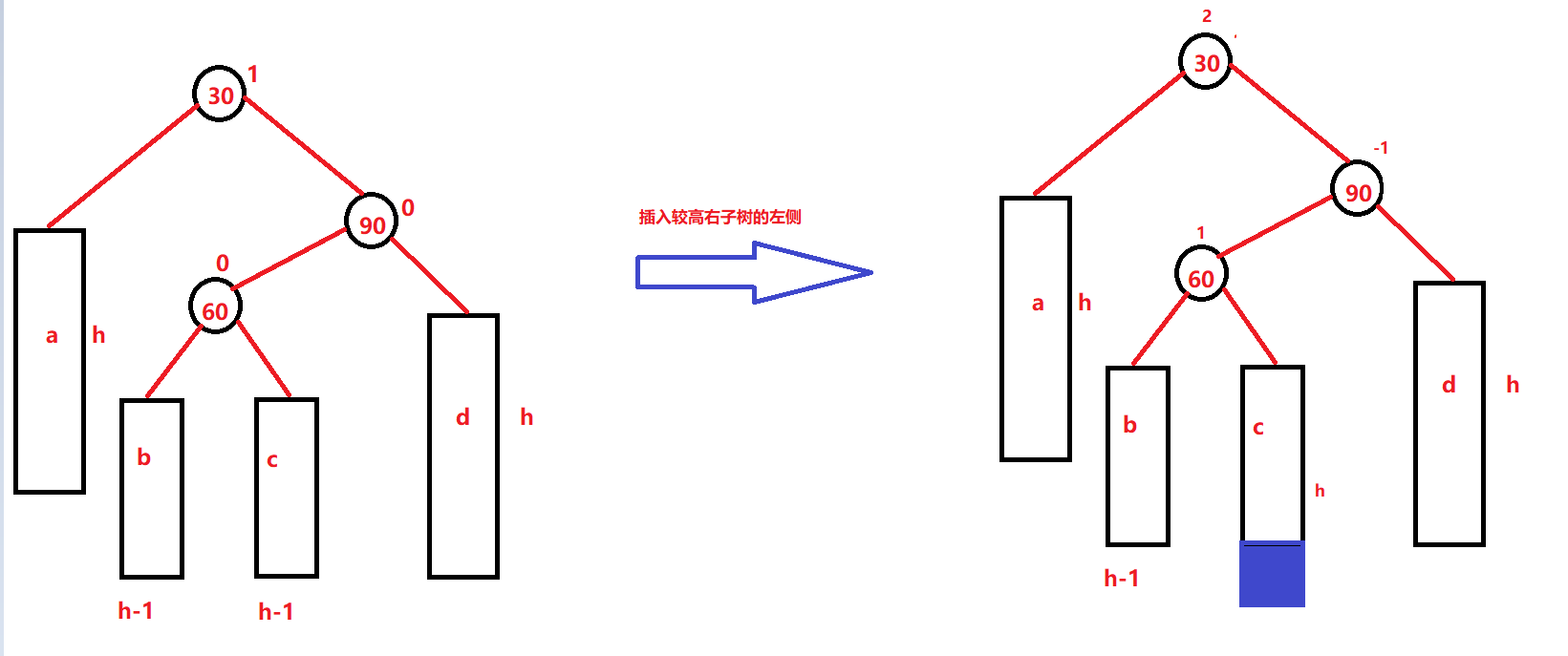
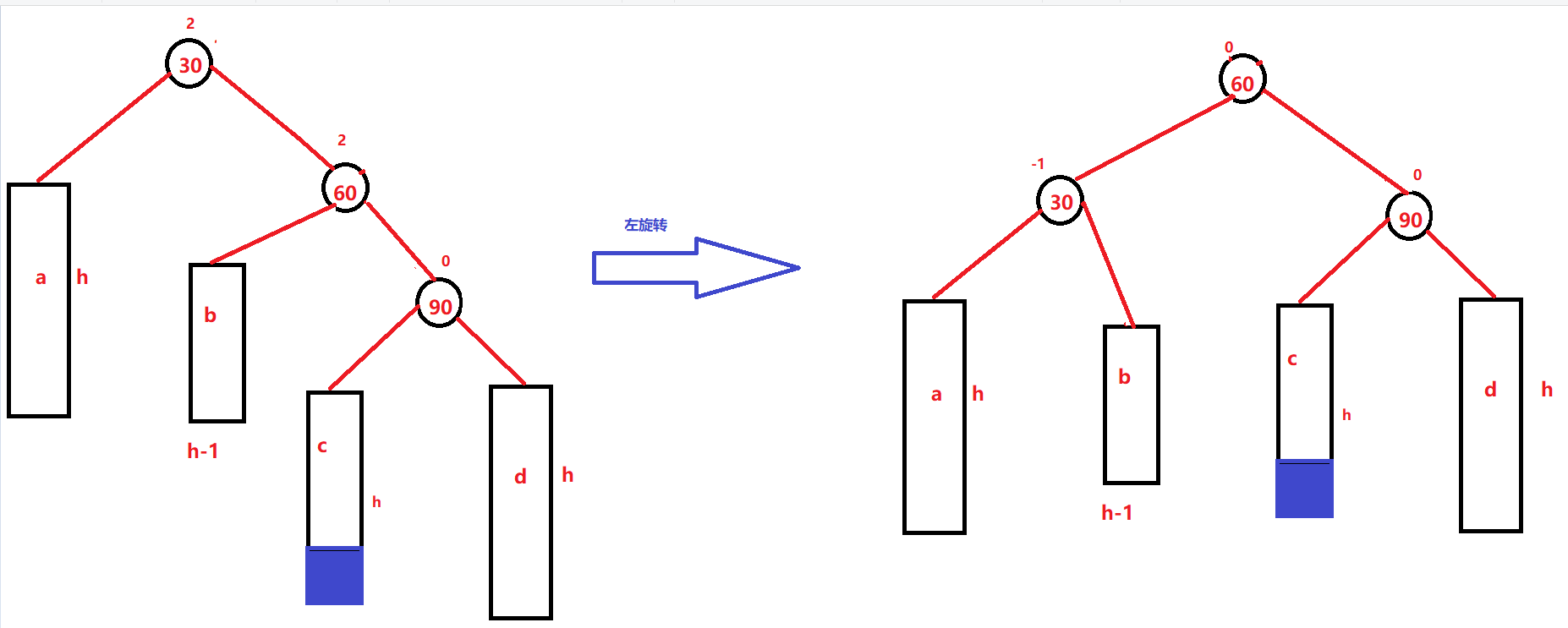
subR为轴点进行右单旋:
parent为轴进行左单旋:
既右左双旋:
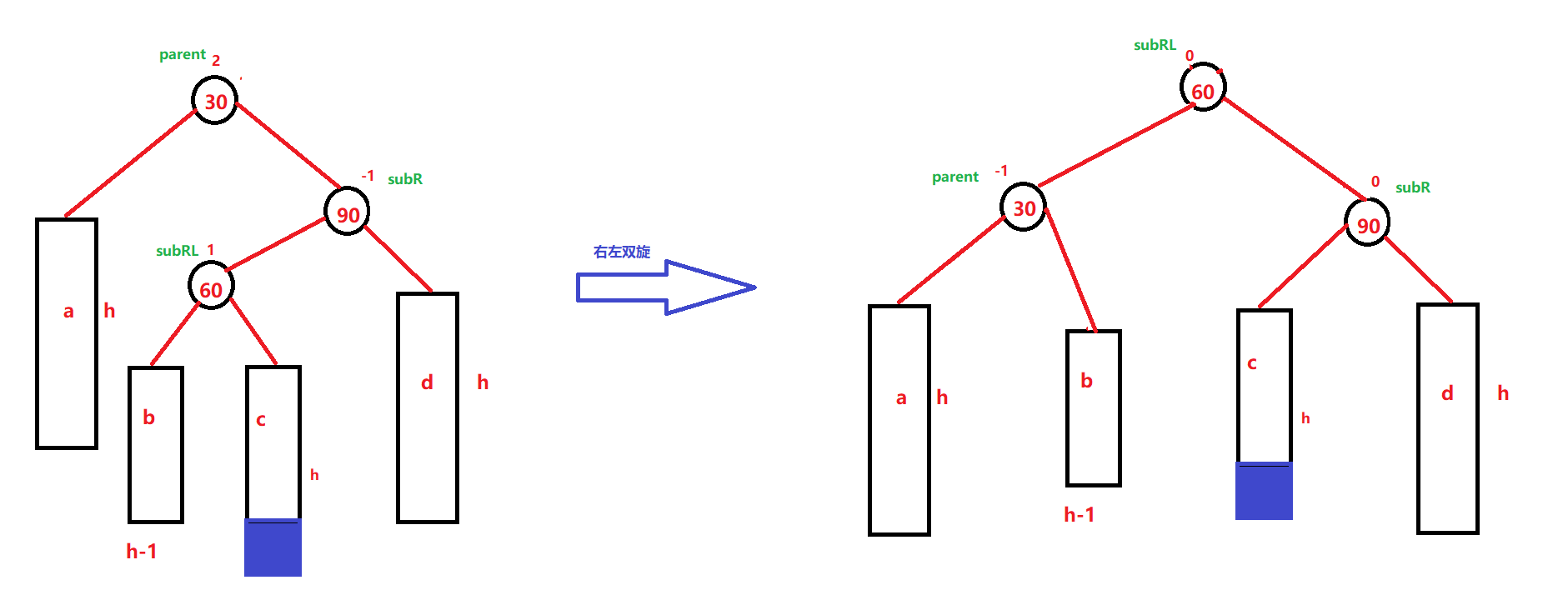
右左双旋后,根据subRL 初始平衡因子的不同分为三种情况分别对应subRL = 0、1、-1情况,与左右双旋情况类似。
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}}
五、进行验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}
-
验证其为平衡树
每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)节点的平衡因子是否计算正确如果是空树,是AVL树;高度差不大于2,并且递归左右子树的高度差都不大于2,也是AVL树;判断平衡因子和该点的高度差是否相等
//求高度
int Height(Node* root){if (root == nullptr)return 0;int lh = Height(root->_left);int rh = Height(root->_right);return lh > rh ? lh + 1 : rh + 1;}
//判断平衡
bool IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}
六、AVLTree的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度即log2( N) 。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。
因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合.
送上源码:
#pragma once
#include <iostream>
#include <assert.h>
#include <time.h>
using namespace std;
template<class K,class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//balance factorAVLTreeNode(const pair<K,V>&kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template <class K,class V>
struct AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//更新平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if(parent->_bf==2||parent->_bf==-2){//左旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右旋else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//左右双旋else if (parent-> _bf == -2&&cur->_bf==1){RotateLR(parent);}//右左双旋else if (parent->_bf ==2&&cur->_bf ==-1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}parent->_bf = subR->_bf = 0;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subL;subL->_right = parent;//if(_root==parent)if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;}//左右双旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR ->_bf;RotateL(parent->_left);RotateR(parent);//更新平衡因子if (bf == -1)//b插入,subLR左子树新增{subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1)//c插入,subLR右子树新增{parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == 0)//subLR自己新增加{parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}//右左双旋void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}}void InOrder(){_InOrder(_root);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}int Height(Node* root){if (root == nullptr)return 0;int lh = Height(root->_left);int rh = Height(root->_right);return lh > rh ? lh + 1 : rh + 1;}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}
private:Node* _root = nullptr;
};//测试
void TestAVLTree()
{//int a[] = { 8,3,1,10,6,4,7,14,13 };//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4,2,6,1,3,5,15,7,16,14 };AVLTree<int, int> t;for (auto e : a){t.Insert(make_pair(e,e));}t.InOrder();cout << t.IsBalance() << endl;
}void TestAVLTree2()
{srand(time(0));const size_t N = 100000;AVLTree<int, int> t;for (size_t i = 0; i < N; i++){size_t x = rand();t.Insert(make_pair(x, x));}//t.InOrder();cout << t.IsBalance() << endl;
}
本篇结束…
相关文章:

【C++】AVLTree——高度平衡二叉搜索树
文章目录一、AVL树的概念二、AVL树节点的定义三、AVL树的插入四、AVL树的旋转1.左单旋2.右单旋3.左右双旋4.右左双旋五、进行验证六、AVLTree的性能个人简介📝 🏆2022年度博客之星Top18;🏆2022社区之星Top2;的🥇C/C领域优质创作者…...
软考中级-嵌入式系统设计师(二)
1、逻辑电路:组合逻辑单路、时序逻辑电路。根据电路是否有存储功能判断。 2、组合逻辑电路 指该电路在任一时刻的输出,仅取决于该时刻的输入信号,而与输入信号作用前电路的状态无关。一般由门电路组成,不含记忆元器件࿰…...

epoll 笔记
maxevents 参数大小一般不超过64必须够了 maxevents 个事件,才会传到用户空间吗?可见,只要有事件就可以传到用户空间。一台服务器可以支撑多少个链接https://blog.csdn.net/mijichui2153/article/details/81331345 0、两台虚拟机的初始状态如…...

vue(5)
文章目录1. 监测数据原理1.1 通过问题引出1.2 开始1.3 Vue.set() 方法1.4 vue 监视 数组1.5 小练习2. 收集表数据3. 过滤器4. 内置指令4.1 v-text4.2 v-html4.3 v-cloak4.4 v-once4.5 v-pre1. 监测数据原理 1.1 通过问题引出 1.2 开始 要想解决上面的这个问题 ,需要…...
Android OTA 相关工具(一) 虚拟 A/B 之 snapshotctl
Android 虚拟 A/B 分区推出快三年了,不论是 google 还是百度结果,除了源代码之外,竟然没有人提到这个 Android Virtual A/B 的调试工具 ,着实让人感觉意外。 所以我相信还有不少人不知道 Android OTA 到底都有哪些调试工具&#…...
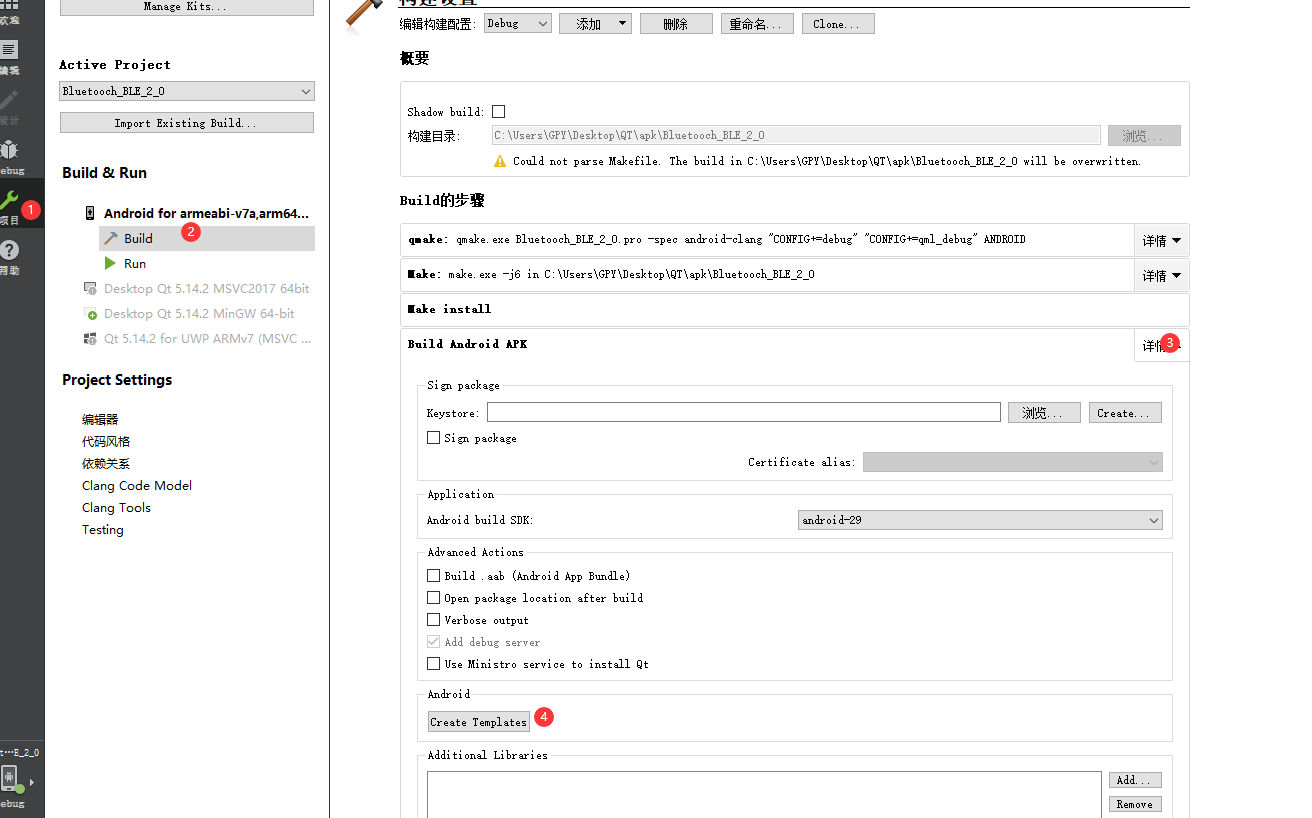
QT for Android BLE Bluetooch QT BLE
小白式的介绍,很详细了,很多主要内容写在程序的注释里,慢慢看 下面是我的源码 https://download.csdn.net/download/qq_27620407/87464307 源码打不开的话可以试试下图的操作,之后电机确定,可能是加图标搞的࿰…...

【蓝桥集训】第四天——双指针
作者:指针不指南吗 专栏:Acwing 蓝桥集训每日一题 🐾或许会很慢,但是不可以停下🐾 文章目录1.字符串删减2.最长连续不重复子序列3.数组元素的目标和1.字符串删减 给定一个由 n 个小写字母构成的字符串。 现在ÿ…...

List<Map<String, Object>>的数据结构的添加和删除实例
对List<Map<String, Object>>的数据结构的添加和删除实例添加//初始化List<Map<String, Object>> products new ArrayList<Map<String,Object>>();//也可以这样初始化List<Map<String, Object>> products null//初始Map<…...

5.2 线程实际案例练习
文章目录1.概述2.实现方案一:继承Thread2.1 代码实现2.2 代码分析3.实现方案二:实现Runnable接口3.1 代码实现3.2 代码分析4.实现方案三:构建线程池4.1 代码实现4.2 代码分析1.概述 接下来我们通过一个售票案例的实际操作来深入理解线程的相…...

stm32f407探索者开发板(十七)——串口寄存器库函数配置方法
文章目录一、STM32串口常用寄存器和库函数1.1 常用的串口寄存器1.2 串口相关的库函数1.3 状态寄存器(USART_ SR)1.4 数据寄存器(USART_ DR)1.5 波特率寄存器(USART_BRR)二、串口配置一般步骤一、STM32串口常…...

山西省2023年软考报名3月14日开始
根据2023年上半年计算机技术与软件专业技术资格(水平)考试工作计划,可以得知,全国考务管理服务平台将于2023年3月13日开放,各地开始组织报名,如山西已发布2023上半年报名简章,从3月14号开始报名。 软考报名官网 大部…...
进程章节总结性实验
进程实验课笔记 本节需要有linux基础,懂基本的linux命令操作即可。 Ubuntu镜像下载 https://note.youdao.com/s/VxvU3eVC ubuntu安装 https://www.bilibili.com/video/BV1j44y1S7c2/?spm_id_from333.999.0.0 实验环境ubuntu22版本,那个linux环境都可以…...

【MyBatis】MyBatis的缓存
10、MyBatis的缓存 10.1、MyBatis的一级缓存 一级缓存是SqlSession级别的,通过同一个SqlSession查询的数据会被缓存,下次查询相同的数据,就会从缓存中直接获取,不会从数据库重新访问 使一级缓存失效的四种情况: 不…...
MyBatis基本使用
一、简介 MyBatis 中文文档 https://mybatis.org/mybatis-3/zh/index.html 1.什么是 MyBatis 概述:MyBatis 是一款优秀的持久层框架,它支持自定义 SQL、存储过程以及高级映射。MyBatis 免除了几乎所有的 JDBC 代码以及设置参数和获取结果集的工作。MyBa…...

如何运行YOLOv6的代码实现目标识别?
YOLOv6是由美团视觉团队开发的1.环境配置我们先把YOLOv6的代码clone下来git clone https://github.com/meituan/YOLOv6.git安装一些必要的包pip install pycocotools2.0作者要求pytorch的版本是1.8.0,我的环境是1.7.0,也是可以正常运行的pip install -r requirement…...
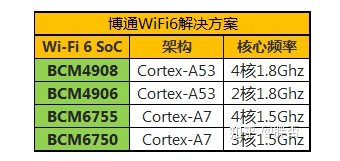
新品BCM6755A1KFEBG/MT7921LE/MT7921AU WiFi芯片
博通在WiFi市场具有相当的实力。在WiFi6上有下面这几个解决方案:型号:BCM6755 BCM6755A1KFEBG类型:四核1.5GHz CPU封装:BGA批次:新BCM6755和BCM6750还是A7架构,更多的用在中低端型号上。BCM6755和BCM6750 C…...

析构函数、拷贝构造
1、析构函数析构函数的定义方式函数名和类名相同,在类名前加~,没有返回值类型,没有函数形参(不能重载)当对象生命周期结束的时候,系统会自动调用析构函数先调用析构函数,再释放对象的空间析构函…...

光学镜头是制作过程阶段理解
光学镜头是由多组镜片组合而成,它是摄影机投影一及显微镜上必不可少的部件。那么光学镜头是如何制造的呢?光学镜头的制作分为以下四个阶段:第一、首先将一大块光学玻璃用钻石锯片进行切片,然后用钻头在每一块玻璃切片上钻出多块冰…...

实验室设计|实验室设计要点SICOLAB
一、实验室设计规划要素1、实验室布局:实验室的布局要符合实验室工作流程,可以将实验室划分为干净区和污染区,以确保实验室的卫生和实验的准确性。2、设备选购:根据实验需要选择适当的设备,并确保设备的质量和性能符合…...
I.MX6ULL_Linux_系统篇(16) uboot分析-启动流程
原文链接:I.MX6ULL_系统篇(16) uboot分析-启动流程 – WSY Personal Blog (cpolar.cn) 前面我们详细的分析了 uboot 的顶层 Makefile,了解了 uboot 的编译流程。本章我们来详细的分析一下 uboot 的启动流程,理清 uboot 是如何启动的。通过对 …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
