【从零学习python 】64. Python正则表达式中re.compile方法的使用详解
文章目录
- re.compile方法的使用
- 进阶案例
re.compile方法的使用
在使用正则表达式时,我们可以直接调用re模块的match、search、findall等方法,并传入指定的正则表达式进行匹配。另外,我们还可以使用re.compile方法生成一个正则表达式对象,然后调用这个对象的相关方法来实现匹配操作。
示例代码如下:
import re# 使用re.match方法直接匹配
re.match(r'h', 'hello')# 或者使用re.compile方法生成Pattern对象,再调用Pattern对象的match方法
regex = re.compile(r'h')
regex.match('hello')re.search(r'l', 'hello')regex = re.compile(r'l')
regex.search('hello')regex = re.compile(r'l')
regex.findall('hello')regex = re.compile(r'l')
regex.finditer('hello')
通过使用re.compile方法生成Pattern对象,我们可以复用编译好的正则表达式,提高多次匹配的效率。同时,这种方式也使得代码更加清晰易读,便于维护和修改。
注意:在使用re.compile方法生成Pattern对象时,需要将正则表达式的字符串作为参数传入,这样可以确保正则表达式的正确性。
进阶案例
【Python】Python 实现猜单词游戏——挑战你的智力和运气!
【python】Python tkinter库实现重量单位转换器的GUI程序
【python】使用Selenium获取(2023博客之星)的参赛文章
【python】使用Selenium和Chrome WebDriver来获取 【腾讯云 Cloud Studio 实战训练营】中的文章信息
使用腾讯云 Cloud studio 实现调度百度AI实现文字识别
【玩转Python系列【小白必看】Python多线程爬虫:下载表情包网站的图片
【玩转Python系列】【小白必看】使用Python爬取双色球历史数据并可视化分析
【玩转python系列】【小白必看】使用Python爬虫技术获取代理IP并保存到文件中
【小白必看】Python图片合成示例之使用PIL库实现多张图片按行列合成
【小白必看】Python爬虫实战之批量下载女神图片并保存到本地
【小白必看】Python词云生成器详细解析及代码实现
【小白必看】Python爬取NBA球员数据示例
【小白必看】使用Python爬取喜马拉雅音频并保存的示例代码
【小白必看】使用Python批量下载英雄联盟皮肤图片的技术实现
【小白必看】Python爬虫数据处理与可视化
【小白必看】轻松获取王者荣耀英雄皮肤图片的Python爬虫程序
【小白必看】利用Python生成个性化名单Word文档
【小白必看】Python爬虫实战:获取阴阳师网站图片并自动保存
小白必看系列之图书管理系统-登录和注册功能示例代码
小白实战100案例: 完整简单的双色球彩票中奖判断程序,适合小白入门
使用 geopandas 和 shapely(.shp) 进行地理空间数据处理和可视化
使用selenium爬取猫眼电影榜单数据
图像增强算法Retinex原理与实现详解
爬虫入门指南(8): 编写天气数据爬虫程序,实现可视化分析
爬虫入门指南(7):使用Selenium和BeautifulSoup爬取豆瓣电影Top250实例讲解【爬虫小白必看】
爬虫入门指南(6):反爬虫与高级技巧:IP代理、User-Agent伪装、Cookie绕过登录验证及验证码识别工具
爬虫入门指南(5): 分布式爬虫与并发控制 【提高爬取效率与请求合理性控制的实现方法】
爬虫入门指南(4): 使用Selenium和API爬取动态网页的最佳方法
爬虫入门指南(3):Python网络请求及常见反爬虫策略应对方法
爬虫入门指南(2):如何使用正则表达式进行数据提取和处理
爬虫入门指南(1):学习爬虫的基础知识和技巧
深度学习模型在图像识别中的应用:CIFAR-10数据集实践与准确率分析
Python面向对象编程基础知识和示例代码
MySQL 数据库操作指南:学习如何使用 Python 进行增删改查操作
Python文件操作指南:编码、读取、写入和异常处理
使用Python和Selenium自动化爬取 #【端午特别征文】 探索技术极致,未来因你出“粽” # 的投稿文章
Python多线程与多进程教程:全面解析、代码案例与优化技巧
Selenium自动化工具集 - 完整指南和使用教程
Python网络爬虫基础进阶到实战教程
Python入门教程:掌握for循环、while循环、字符串操作、文件读写与异常处理等基础知识
Pandas数据处理与分析教程:从基础到实战
Python 中常用的数据类型及相关操作详解
【2023年最新】提高分类模型指标的六大方案详解
Python编程入门基础及高级技能、Web开发、数据分析和机器学习与人工智能
用4种回归方法绘制预测结果图表:向量回归、随机森林回归、线性回归、K-最近邻回归
相关文章:

【从零学习python 】64. Python正则表达式中re.compile方法的使用详解
文章目录 re.compile方法的使用进阶案例 re.compile方法的使用 在使用正则表达式时,我们可以直接调用re模块的match、search、findall等方法,并传入指定的正则表达式进行匹配。另外,我们还可以使用re.compile方法生成一个正则表达式对象&…...
【FAQ】视频云存储/安防监控EasyCVR视频汇聚平台如何通过角色权限自行分配功能模块?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。音视频流媒体视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、…...
基于Spring Boot的社区诊所就医管理系统的设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的社区诊所就医管理系统的设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java …...

mysql从传统模式切到GTID模式后启动主从,主从异常报错1236
一 前言 MySQL 的主从复制作为一项高可用特性,用于将主库的数据同步到从库,在维护主从复制数据库集群的时候,作为专职的MySQL DBA,笔者相信大多数人都会遇到“Got fatal error 1236 from master when reading data from binary …...
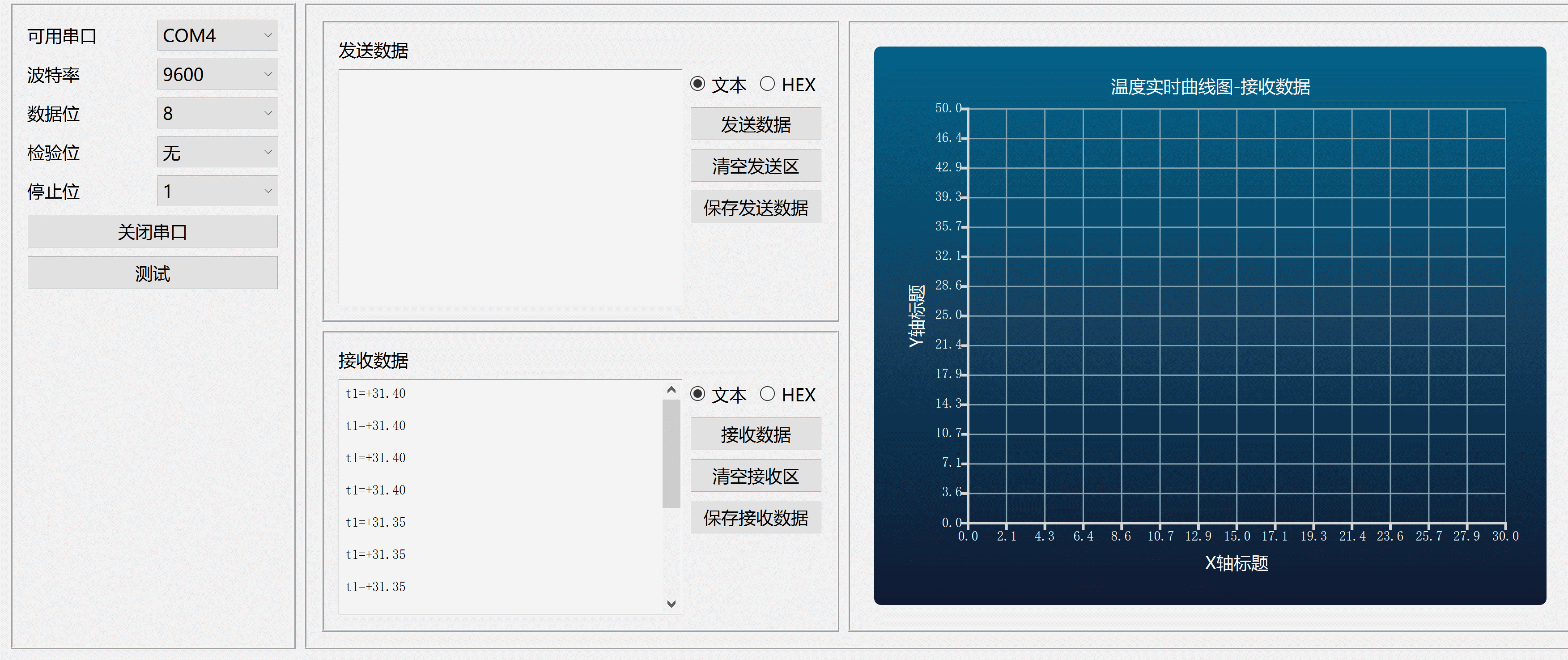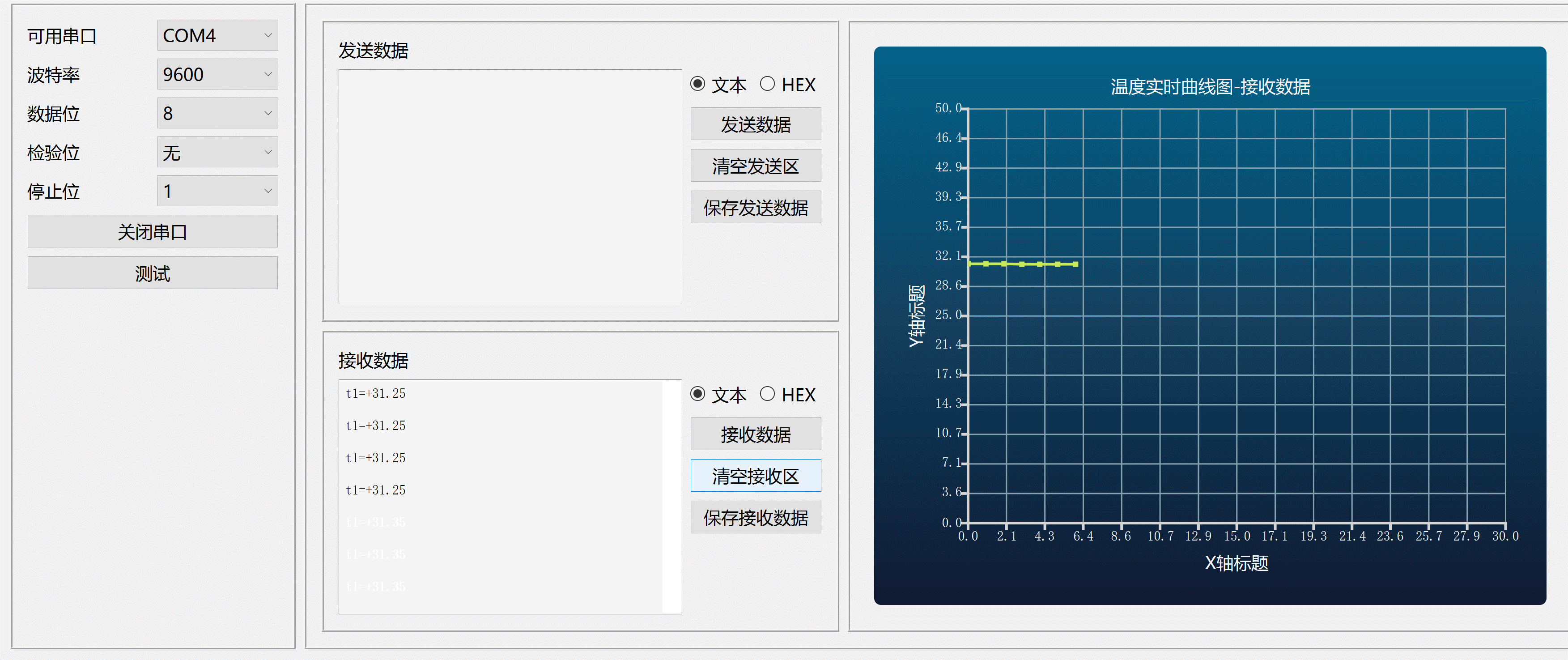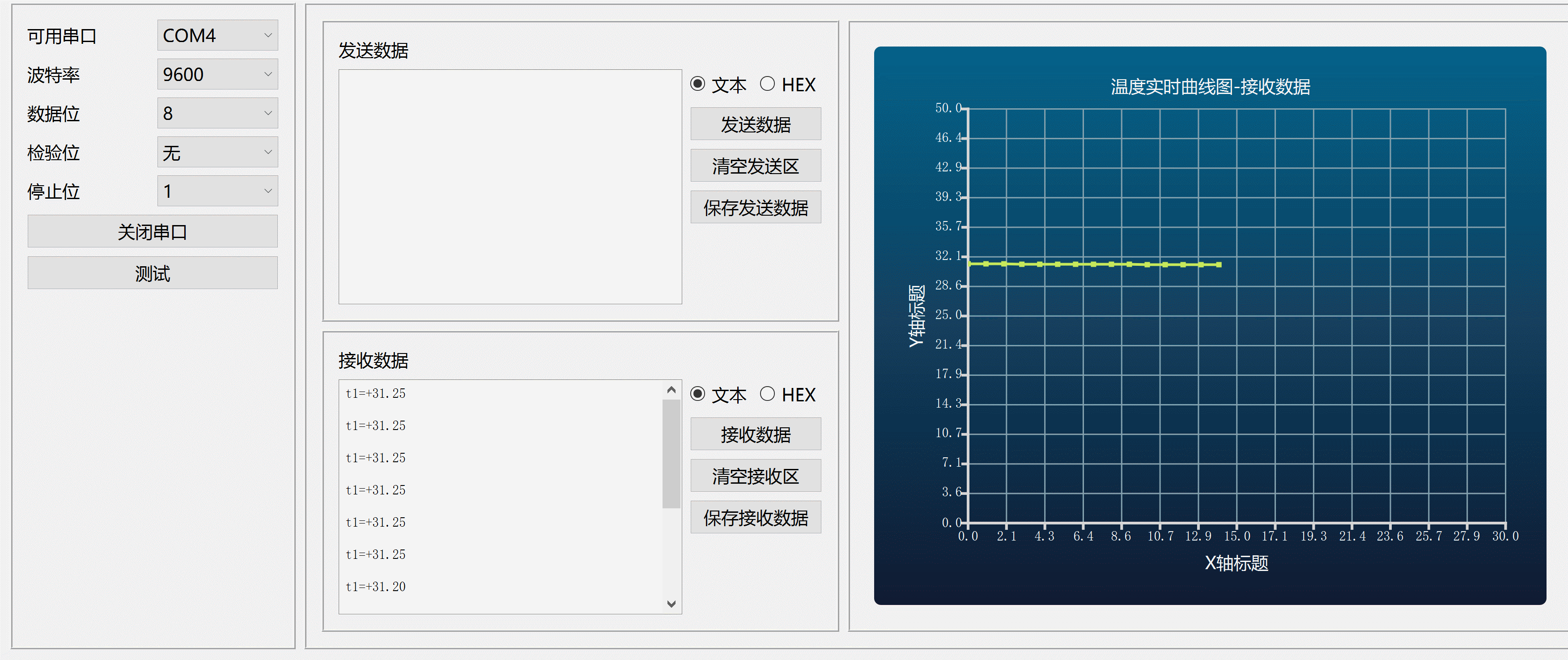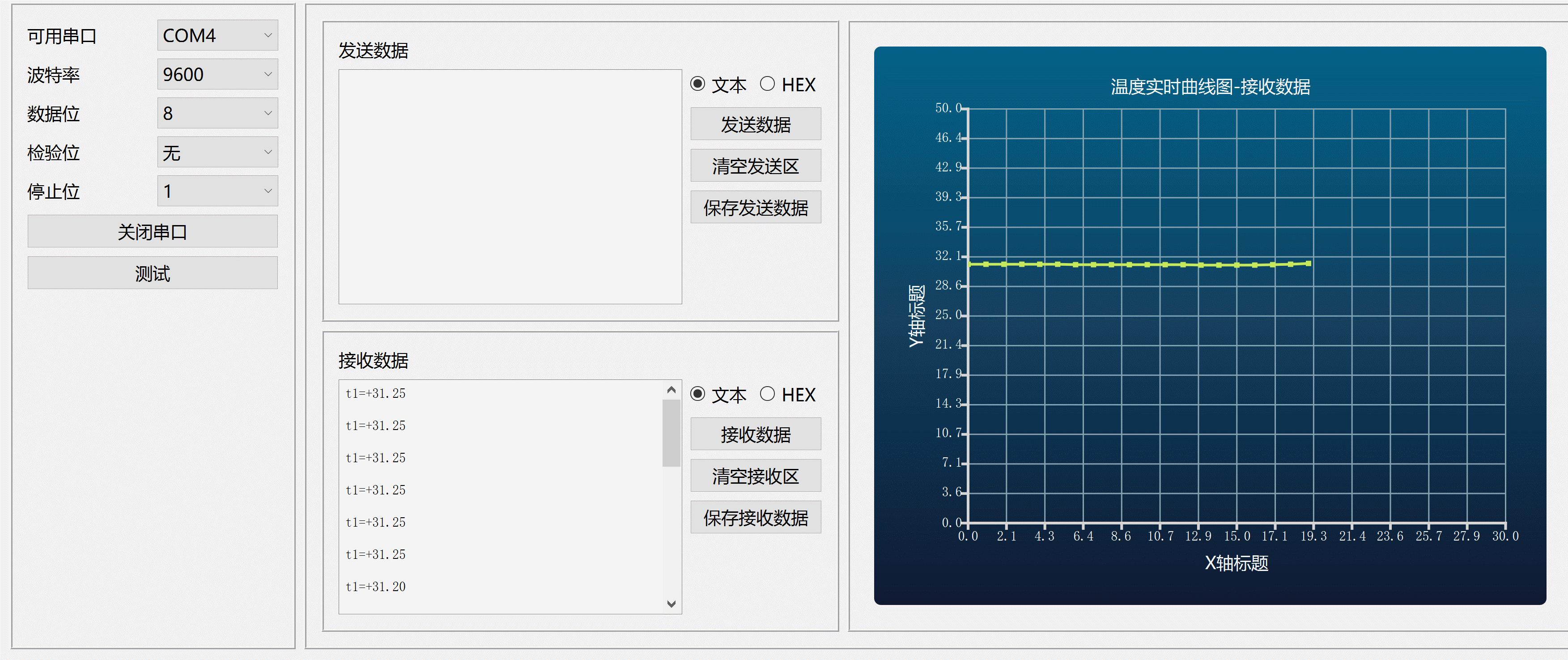
Qt+C++串口调试接收发送数据曲线图
程序示例精选 QtC串口调试接收发送数据曲线图 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对<<QtC串口调试接收发送数据曲线图>>编写代码,代码整洁,规则&…...

【从零学习python 】75. TCP协议:可靠的面向连接的传输层通信协议
文章目录 TCP协议TCP通信的三个步骤TCP特点TCP与UDP的区别TCP通信模型进阶案例 TCP协议 TCP协议,传输控制协议(英语:Transmission Control Protocol,缩写为 TCP)是一种面向连接的、可靠的、基于字节流的传输层通信协议…...

IPv4 基础概念
IPv4 基础概念 IPv4 广播地址 广播是一种通信方式,用于将数据包发送到同一网络中的所有设备。在广播中,数据包被发送到特殊的广播地址,例如在IPv4中,广播地址通常为特定子网的广播地址(例如,192.168.1.0/…...
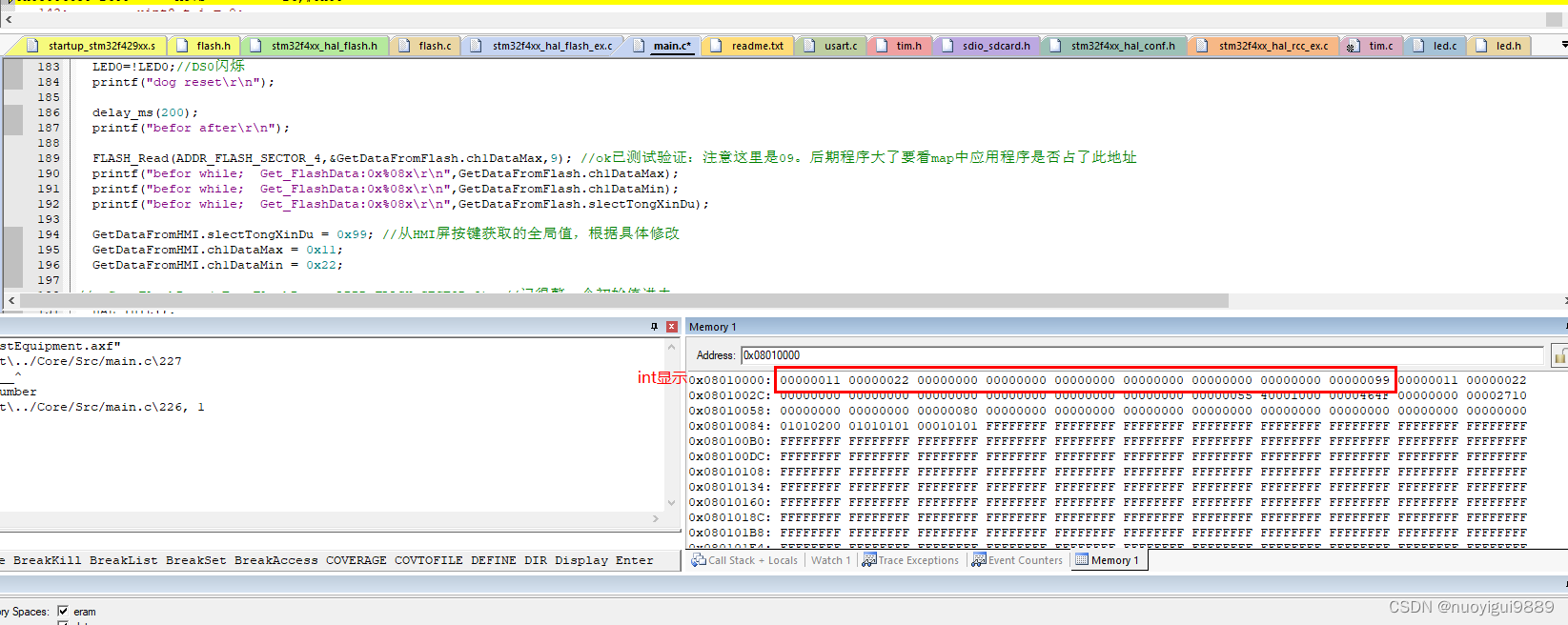
stm32片内读写项目总结(多字节读写tongxindu)
1.flash操作驱动程序 a头文件 #ifndef FLASH_H #define FLASH_H #include “stm32f4xx.h” #define BOARD_NUM_ADDR 0x0800C000 #define STM32_FLASH_BASE 0x08000000 //STM32 FLASH的起始地址 #define FLASH_WAITETIME 50000 //FLASH等待超时时间 //FLASH 扇区的起始地址…...

ECMAScript6 简介及拓展
ECMAScript简介 JavaScript是大家所了解的语言名称, 但它的正式名称叫做ECMAScript。 1996年11月, JavaScript的创造者网景公司将JavaScript提交给国际化组织 ECMA(欧洲计算机制造联合会), 希望这种语言能够成为国际标准。 随后 ECMA 发布…...

可视化构建包分析报告
一、webpack 使用 webpack-bundle-analyzer 插件即可。 安装:npm install webpack-bundle-analyzer -D 使用:new BundleAnalyzerPlugin(options?: object) Name Type Description analyzerMode One of: server, static, json, disabled Default: se…...
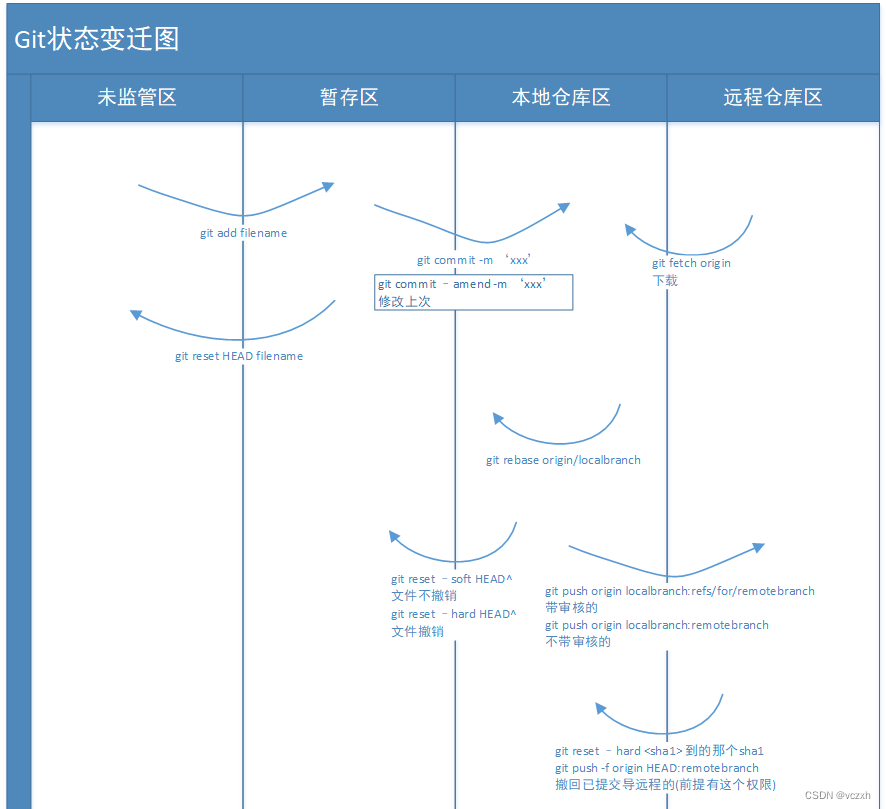
统一git使用方法,git状态变迁图,git commit提交规范
目录 说明 统一git使用方法 git状态变迁图 git commit 提交规范 说明 多次工作中多名员工不懂git多次技术分享,自行查资料学习git并使用,会出现使用各种偏僻的命令,异常问题无法解决;或出现带url的git合并提交。主要是学的不…...

react与vue的区别
React和Vue.js是两个流行的JavaScript库/框架,用于构建用户界面。以下是React和Vue之间的一些主要区别: 学习曲线:Vue.js对于新手来说比React更容易学习和上手。 构建方式:React强调组件的可重用性,而Vue.js更注重模板…...

成功解决SQL 错误 [22000]: 第3 行附近出现错误: 试图修改自增列[ID](达梦数据库)
当我们使用工具来手动修改自增列的自增ID时,可能会报如下异常 SQL 错误 [22000]: 第3 行附近出现错误:试图修改自增列[ID] 解决办法: 可以使用SQL语句来修改 ALTER TABLE "fdw"."SYSTEM_DICT_TYPE" DROP IDENTITY; UPDATE "f…...

【算法】活用双指针完成复写零操作
Problem: 1089. 复写零 文章目录 题目解析算法原理分析找到最后一个复写的位置从后往前进行复写操作 代码展示 题目解析 首先我们来分析一下本题的题目意思 可以看到题目中给到了一个数组,意思是让我们将数组中的零元素都复写一遍,然后将其余的元素向后平…...
【面试高频题】难度 3/5,字典树热门运用题
题目描述 这是 LeetCode 上的 「745. 前缀和后缀搜索」 ,难度为 「困难」。 Tag : 「字典树」 设计一个包含一些单词的特殊词典,并能够通过前缀和后缀来检索单词。 实现 WordFilter 类: WordFilter(string[] words) 使用词典中的单词 words 初…...

vue base64图片转file流 下载到本地 或者上传
<img :src"data:image/png;base64,form.img" style"max-width:280px;max-height: 280px;margin: auto;" />// base64 转file const base64ToFile()>{let byImg atob(form.img); // 解码base64let n byImg.lengthlet a new Uint8Array(n);while…...

无涯教程-PHP - 简介
PHP 7是最期待的,它是PHP编程语言的主要功能版本。 PHP 7于2015年12月3日发布。本教程将以简单直观的方式教您PHP 7的新功能及其用法。 无涯教程假设您已经了解旧版本的PHP,现在就可以开始学习PHP 7的新功能。 使用下面的示例- <html><head&…...

web基础+HTTP协议+httpd详细配置
目目录录 一、Web基础1.1 HTML概述1.1.1 HTML的文件结构1.1.2 HTML中的部分基本标签 1.3 MIME1.4 URI 和 URL1.4 定义1.4.2 URI 和 URL 的区别 二、静态资源和动态资源2.1 静态资源2.2 动态资源 三、HTTP协议3.1 HTTP协议简介3.2 HTTP协议版本3.2 HTTP方法3.3 HTTP请求访问的完…...

【sql】MongoDB的增删改查分页条件等
【sql】MongoDB的增删改查分页条件等 //增 //新增数据2种方式 db.msg.save({"name":"springboot😀"}); db.msg.insert({"name":"mango good"}); db.msg.save({"name":"springboot",type:"工具书&…...
)
我的动态归纳(便于搜索)
linux dns配置文件是“/etc/resolv.conf”,该配置文件用于配置DNS客户,它包含了主机的域名搜索顺序和DNS/服务器的地址,每一行包括一个关键字和一个或多个空格隔开的参数。 /etc/resolv.conf (不配置就不能域名解析) 可…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
