GraphScope,开源图数据分析引擎的领航者
文章首发地址

GraphScope是一个开源的大规模图数据分析引擎,由Aliyun、阿里巴巴集团和华为公司共同开发。GraphScope旨在为大规模图数据处理和分析提供高性能、高效率的解决方案。
Github地址:
https://github.com/alibaba/GraphScope
GraphScope 的重要特点
- 分布式计算引擎: GraphScope基于分布式计算框架Apache Flink和Apache Vineyard构建,能够在分布式集群上高效地处理大规模图数据。
- 常见图计算算法支持: GraphScope提供了丰富的图计算算法库,包括PageRank、SSSP(Single Source Shortest Path)、Connected Components等常用算法,方便用户进行图数据分析。
- 可扩展性: GraphScope支持水平扩展,可以在多个计算节点上分布式执行计算任务,以应对大规模图数据处理需求。
- 可视化分析工具: GraphScope提供了可视化的数据探索和分析工具,用户可以通过图形界面进行数据预览、交互式查询和结果展示。
- 开放性和易用性: GraphScope采用图计算领域通用的开放标准,如Graph Computer API、Graph Data Format等,使得用户可以方便地使用已有的图计算资源和工具。
GraphScope 的应用潜力
- 社交网络分析: GraphScope可以帮助用户分析社交网络结构、发现社区、识别关键节点等,为社交网络平台提供更好的用户体验和精准推荐。
- 金融风控: GraphScope可以应用于金融领域的反欺诈、风险控制等场景,帮助识别异常交易、构建用户画像等。
- 物联网数据分析: GraphScope可以处理物联网设备产生的海量数据,帮助用户发现设备之间的关联关系、进行智能调度等。
相关文章:

GraphScope,开源图数据分析引擎的领航者
文章首发地址 GraphScope是一个开源的大规模图数据分析引擎,由Aliyun、阿里巴巴集团和华为公司共同开发。GraphScope旨在为大规模图数据处理和分析提供高性能、高效率的解决方案。 Github地址: https://github.com/alibaba/GraphScope GraphScope 的重…...
【Linux】邮件服务器搭建 postfix+dovecot+mysql (终极版 超详细 亲测多遍无问题)
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录 前言基础原理准备工作一 、安装关于权…...
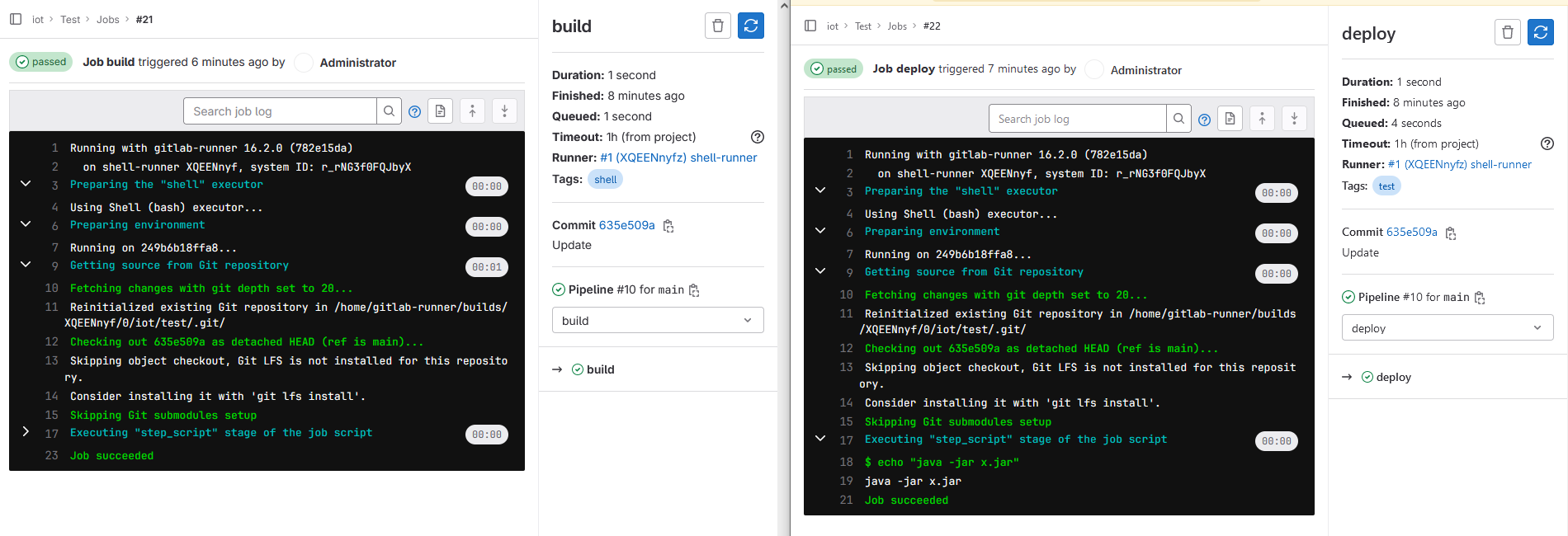
GitLab与GitLab Runner安装(RPM与Docker方式),CI/CD初体验
背景 GitLab 是一个强大的版本控制系统和协作平台,记录一下在实际工作中关于 GitLab 的安装使用记录。 一开始使用 GitLab 时,是在 CentOS7 上直接以 rpm 包的方式进行安装,仅作为代码托管工具来使用,版本: 14.10.4 …...
vue3+element下拉多选框组件
<!-- 下拉多选 --> <template><div class"select-checked"><el-select v-model"selected" :class"{ all: optionsAll, hidden: selectedOptions.data.length < 2 }" multipleplaceholder"请选择" :popper-app…...

Python科研绘图--Task02
目录 图形元素 画布 (fifigure)。 坐标图形 (axes),也称为子图。 轴 (axis) :数据轴对象,即坐标轴线。 刻度 (tick),即刻度对象。 图层顺序 轴比例和刻度 轴比例 刻度位置和刻度格式 坐标系 直角坐标系 极坐标系 地理…...
[保研/考研机试] KY11 二叉树遍历 清华大学复试上机题 C++实现
题目链接: 二叉树遍历_牛客题霸_牛客网编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。题目来自【牛客题霸】https://www.nowcoder.com/share/jump/43719512169254700747…...

【官方中文文档】Mybatis-Spring #简介
简介 什么是 MyBatis-Spring? MyBatis-Spring 会帮助你将 MyBatis 代码无缝地整合到 Spring 中。它将允许 MyBatis 参与到 Spring 的事务管理之中,创建映射器 mapper 和 SqlSession 并注入到 bean 中,以及将 Mybatis 的异常转换为 Spring 的…...
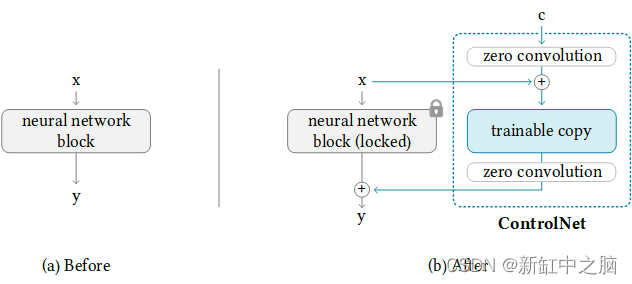
稳定扩散ControlNet v1.1 权威指南
ControlNet 是一种稳定扩散模型,可让你从参考图像中复制构图或人体姿势。 经验丰富的稳定扩散用户知道生成想要的确切成分有多难。图像有点随机。你所能做的就是玩数字游戏:生成大量图像并选择你喜欢的图片。 借助 ControlNet,稳定扩散用户…...
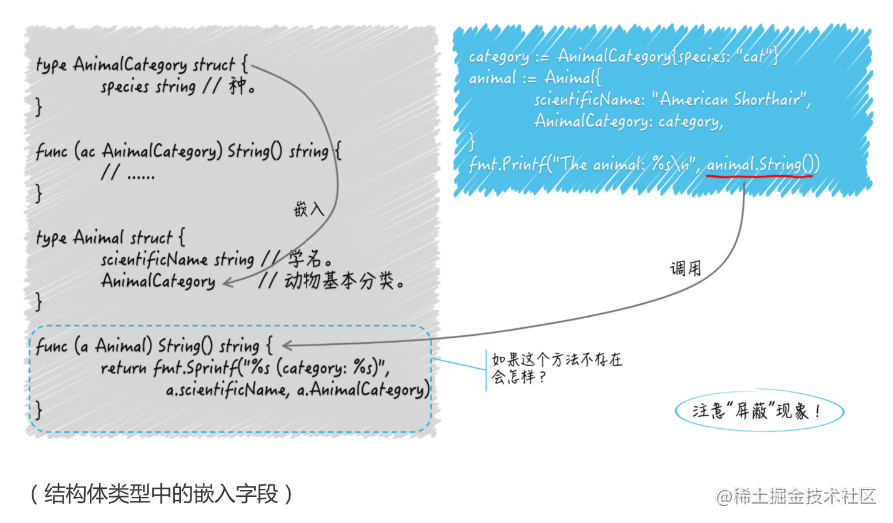
【golang】结构体及其方法的使用(struct)
函数是独立的程序实体。我们可以声明有名字的函数,也可以声明没名字的函数,还可以把它们当做普通的值传来传去。我们能把具有相同签名的函数抽象成独立的函数类型,以作为一组输入、输出(或者说一类逻辑组件)的代表。 …...
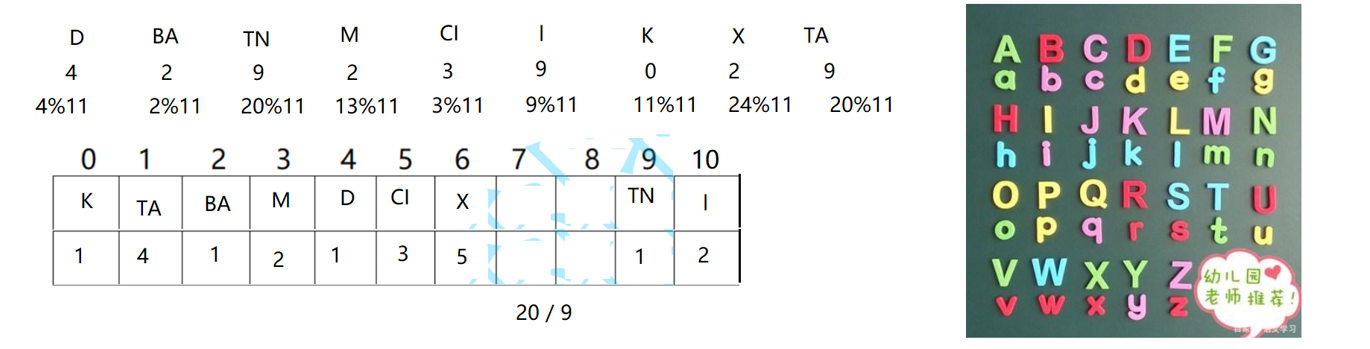
【数据结构】-- 排序算法习题总结
排序 时间复杂度 空间复杂度 稳定性 冒泡排序 O(n^2) 优化后O(n) O(1) 稳定 快速排序 最好O(n*logn) 最坏O(n^2) 最好O(logn) 最坏O(n) 不稳定直接插入排序…...
实战篇)
第十章 CUDA流(stream)实战篇
cuda教程目录 第一章 指针篇 第二章 CUDA原理篇 第三章 CUDA编译器环境配置篇 第四章 kernel函数基础篇 第五章 kernel索引(index)篇 第六章 kenel矩阵计算实战篇 第七章 kenel实战强化篇 第八章 CUDA内存应用与性能优化篇 第九章 CUDA原子(atomic)实战篇 第十章 CUDA流(strea…...
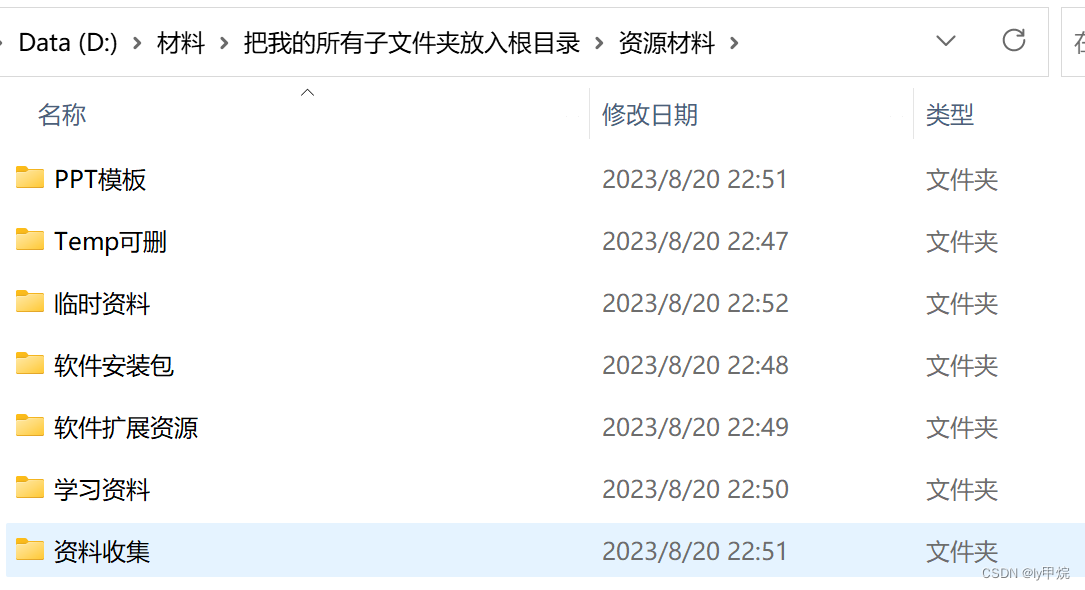
如何进行电脑文件夹分类与整理?
本科电脑用了四年,毕业后发现空间很满,但是真正有用的东西仿佛就一点。好像是在学开发的时候,听到一个老师说,根目录不要放太多文件夹,不然就相当于没有根目录了。刚好研究生有了新的台式电脑,开始有规划的…...
kafka-python 消费者消费不到消息
排除步骤1: 使用group_id”consumer_group_id_001“ 和 auto_offset_reset"earliest" from kafka import KafkaConsumerconsumer KafkaConsumer(bootstrap_servers["dev-kafka01.test.xxx.cloud:9092"],enable_auto_commitTrue, auto_commit…...

穿起“新架构”的舞鞋,跳一支金融数字化转型的华尔兹
华尔兹,是男女两位舞者,通过形体的控制,舞步技巧的发挥,完美配合呈现而出的一种舞蹈形式。华尔兹舞姿,如行云流水、潇洒自如、飘逸优美,素有“舞中皇后”的美称。 在跳华尔兹的时候,如果舞者双…...

SpringBoot 常用注解
随着Spring及Spring Boot的发展,基于Java的配置已经慢慢替代了基于xml的配置形式。本篇文章为大家整理和简介Spring Boot中常用的注解及其功能。 SpringBoot注解 SpringBootApplication:开启Spring Boot自动配置的核心注解,相关等同于Configu…...
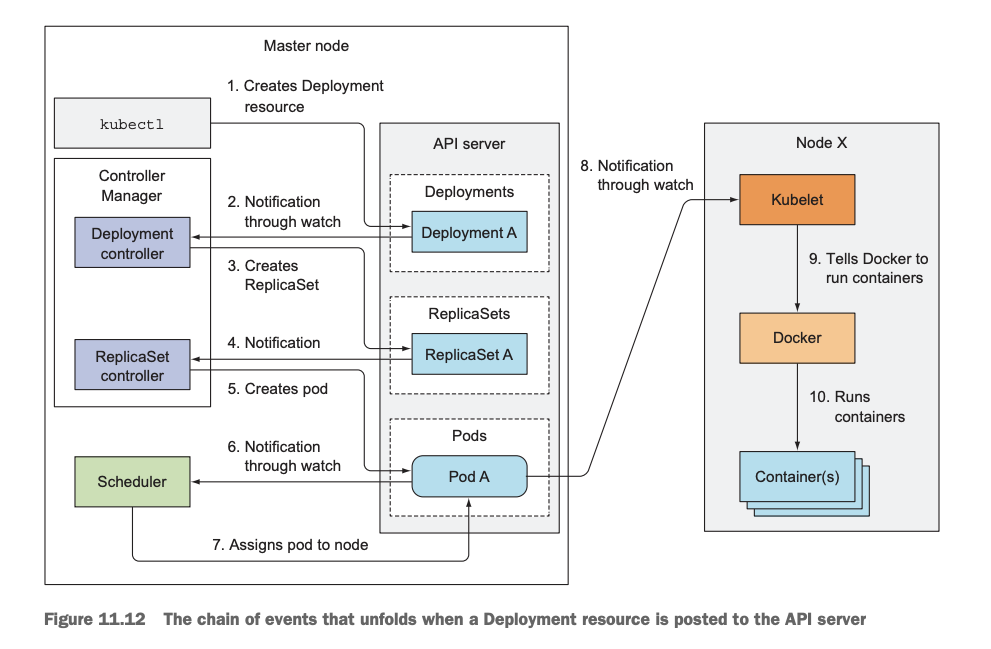
k8s deployment创建pod流程图
参考 k8s 创建pod和deployment的流程 - SoulChild随笔记...

C++ 逗号运算符
使用逗号运算符是为了把几个表达式放在一起。 整个逗号表达式的值为系列中最后一个表达式的值。 从本质上讲,逗号的作用是将一系列运算按顺序执行。 表达式1, 表达式2求解过程是:先求解表达式 1,再求解表达式 2。整个逗号表达式的值是表达…...

jdbc集成phoneix hbase
为什么使用jdbc集成 需求简单,只是往phoneix存储数据原本项目已经有mysql的mybatis plus集成,如果采用dataSource方式就需要采用多数据源的方式,造成架构复杂化,使用复杂化,并且修改地方过多。 Qualifier("phoe…...
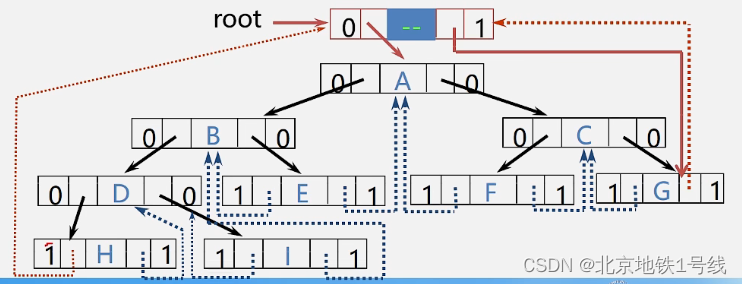
16.遍历二叉树,线索二叉树
目录 一. 遍历二叉树 (1)三种遍历方式 (2)递归遍历算法 (3)非递归遍历算法 (4)层次遍历算法 二. 基于递归遍历算法的二叉树有关算法 (1)二叉树的建立 …...

电商平台按关键字搜索商品淘宝京东拼多多api接口PHP示例
关键词搜索商品接口的作用是通过调用接口来实现在电商平台中进行商品搜索。具体而言,该接口可以提供以下功能和作用: 商品搜索:用户可以通过输入关键词,在电商平台上进行商品搜索。接口可以根据关键词对商品的名称、描述、标签等…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...
