16.遍历二叉树,线索二叉树
目录
一. 遍历二叉树
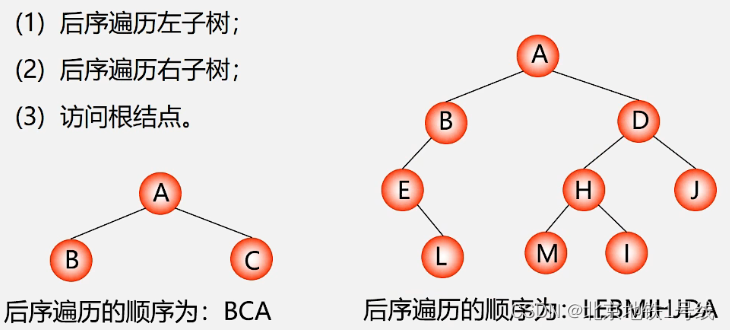
(1)三种遍历方式
(2)递归遍历算法
(3)非递归遍历算法
(4)层次遍历算法
二. 基于递归遍历算法的二叉树有关算法
(1)二叉树的建立
(2)二叉树的复制
(3)二叉树的深度计算
(4)计算二叉树中的结点数
(5)计算二叉树中的叶子结点数
三. 线索二叉树
一. 遍历二叉树
遍历定义——顺着某一条搜索路径巡访二叉树中的结点,使得每个结点均被访问一次,而且仅被访问一次(又称周游)。这里“访问”的含义很广,可以是对结点作各种处理,如:输出结点的信息、修改结点的数据值等,但要求这种访问不破坏原来的数据结构。
遍历目的——得到树中所有结点的一个线性排列。
遍历用途——它是树结构插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。
(1)三种遍历方式
由于二叉树有根结点D,左子树L,右子树R,只要依次访问这三部分,就可以遍历这个二叉树。规定先左后右,即必须先访问左子树,再访问右子树,则根据什么时候访问根结点有:DLR——先(根)序遍历,LDR———中(根)序遍历,LRD———后(根)序遍历三种遍历方式。

由二叉树的递归定义可知,遍历左子树和遍历右子树可如同遍历二叉树一样“递归”进行。



若二叉树中各结点的值均不相同,则二叉树结点的先序序列、中的序列和后序列都是唯一的。
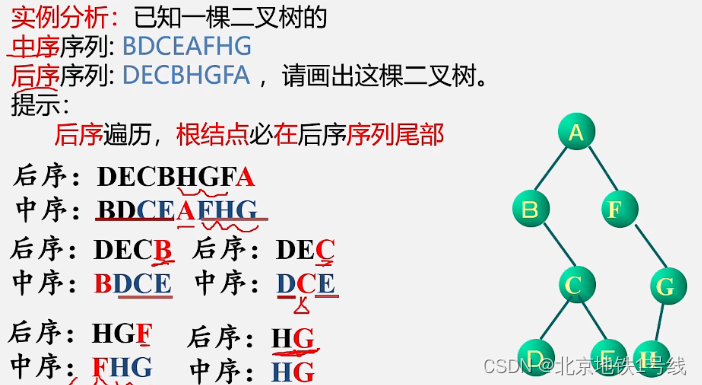
下面我们考虑逆过程:由二叉树的先序序列和中序序列,或由二叉树的后序序列和中序序列可以确定唯一一棵二叉树(只知道前序和后序序列不可以)。
原理:先序(后序)序列的第一个(最后一个)一定是根结点,根结点在中序序列中把整个序列分为两部分,左边序列是左子树,右面序列是右子树。依此类推。
(2)递归遍历算法
下面以先序遍历为例写出递归算法代码。具体解释如下:
-
首先,判断二叉树是否为空(即
T==NULL),如果为空,则直接返回(return OK),因为空树没有节点可遍历。 -
如果二叉树不为空,首先对当前节点
T进行访问操作(visit(T)),即对根节点进行处理。 -
然后,通过递归调用
PreOrderTraverse函数来遍历当前节点的左子树(T->Ichild),即对左子树进行前序遍历。 -
接着,再通过递归调用
PreOrderTraverse函数来遍历当前节点的右子树(T->rchild),即对右子树进行前序遍历。
这样,通过递归的方式,可以依次访问二叉树的根节点、左子树和右子树,实现了前序遍历。
需要注意的是,visit(T) 表示对节点 T 进行访问操作,具体的操作可以根据实际需求来定义。
void PreOrderTraverse(BiTree T){ //前序遍历if(T==NULL) return OK; //空二叉树,这里OK理解为退出到上一层else{visit(T);//访问根结点PreOrderTraverse(T->Ichild);//递归遍历左子树PreOrderTraverse(T->rchild);//递归遍历右子树}
}

同样我们可以很容易的写出中序遍历和后序遍历的算法代码:
void PreOrderTraverse(BiTree T){ //中序遍历if(T==NULL) return OK; //空二叉树else{PreOrderTraverse(T->Ichild);//递归遍历左子树visit(T);//访问根结点PreOrderTraverse(T->rchild);//递归遍历右子树}
}
void PreOrderTraverse(BiTree T){ //后序遍历if(T==NULL) return OK; //空二叉树else{PreOrderTraverse(T->Ichild);//递归遍历左子树PreOrderTraverse(T->rchild);//递归遍历右子树visit(T);//访问根结点}
}
如果去掉输出语句,从递归的角度看,三种算法是完全相同的,或说这三种算法的访问路径是相同的,只是访问结点的时机不同。从图中虚线出发(白点代表左子树或者右子树为空),每个结点都经过了3次。第1次经过时访问=先序遍历,第2次经过时访问=中序遍历,第3次经过时访问=后序遍历。
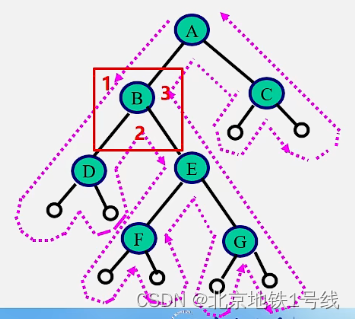
遍历算法的时间复杂度:O(3n)=O(n),每个结点访问一次;
空间复杂度:O(n),对每一个经过但不访问的结点,我们都要找个空间存起来,最坏的情况就是除了根结点外其他所有结点都在右子树上,这时候存全部n个结点。
(3)非递归遍历算法
以中序遍历为例:二叉树中序遍历的非递归算法的关键:在中序遍历过某结点的整个左子树后,如何找到该结点的根以及右子树。
基本思想(中序遍历左子树根结点后进先出):
- 建立一个栈
- 根结点进栈,遍历左子树
- 左子树全部访问完毕,根结点出栈,输出根结点,遍历右子树。

栈的变化情况:A进-B进-B出-D进-D出-A出-C进-C出;
写出代码,具体步骤解释如下:
-
首先,声明一个辅助指针
p和一个栈S,用于存储节点和辅助遍历。 -
初始化栈
S,即将栈置空。 -
将根节点
T赋值给指针p,即将p指向根节点。 -
进入循环,判断条件为
p非空或者栈S非空。只要满足这个条件,就继续遍历二叉树。 -
在循环中,首先判断当前节点
p是否非空。如果非空,则将其入栈(Push(S,p)),并将p指向其左子树(p = p->lchild)。 -
如果当前节点
p为空,即左子树为空,说明已经到达最左边的叶子节点。此时需要从栈中弹出一个节点(Pop(S,q))。 -
对弹出的节点
q进行访问操作,这里使用printf打印出节点的数据(printf("%c",q->data))。 -
将指针
p指向节点q的右子树(p = q->rchild),继续遍历右子树。 -
重复步骤 4-8,直到遍历完整个二叉树。
-
最后,当指针变量p指向NULL,且工作栈中没有元素,说明整个二叉树遍历结束,跳出整个while循环,返回状态值
OK,表示函数执行成功。
Status InOrderTraverse(BiTree T){BiTree p,q; //弄两个指针 InitStack(S); //初始化一个工作栈p=T; //让p指向树的根结点while(p||!StackEmpty(S)){ //StackEmpty()栈为空返回TRUE,否则返回FALSEif(p){Push(S,p);p = p->lchild;}else{Pop(S,q); printf(“%c”,q->data);p = q->rchild;}}//while
return OK;
}
(4)层次遍历算法
二叉树的层次遍历:对于一颗二叉树,从根结点开始,按从上到下、从左到右的顺序访问每一个结点。每一个结点仅仅访问一次。

算法设计思路:使用队列。
I. 将根结点进队;
II. 队不空时循环:从队列中出列一个结点*p,访问它,依次执行下面两步:
- 若它有左孩子结点,将左孩子结点进队;
- 若它有右孩子结点,将右孩子结点进队。
队列变化过程:a进队-a出队,b,f依次进队-b出队,c,d依次进队-f出队,g进队-c出队-d出队,e进队-g出队,h进队-e出队-h出队
使用队列定义类型如下:
typedef struct{BTNode data[MaxSize]; //存放队中元素int front,rear; //队头和队尾指针
}SqQueue; //顺序循环队列类型
给出算法代码,解释如下:
-
首先,声明一个指针
p和一个队列qu,用于存储节点和辅助遍历。 -
初始化队列
qu,即将队列置空。 -
将根结点
b入队列(enQueue(qu,b)),即将根节点放入队列中。 -
进入循环,判断条件为队列
qu非空。只要队列非空,就继续遍历二叉树。 -
在循环中,首先从队列中出队列一个节点(
deQueue(qu,p)),并对该节点进行访问操作,这里使用printf打印出节点的数据(printf(" %c", p->data))。 -
然后,判断当前节点
p的左子节点是否非空。如果非空,则将其入队列(enQueue(qu,p->lchild))。 -
接着,判断当前节点
p的右子节点是否非空。如果非空,则将其入队列(enQueue(qu,p->rchild))。 -
重复步骤 4-7,直到遍历完整个二叉树。
-
最后,返回结果。
void LevelOrder(BTNode *b) {BTNode *p; //p指向队列头部用于出队列SqQueue qu;InitQueue(qu); //初始化队列enQueue(qu,b); //根结点指针进入队列while(!QueueEmpty(qu)){ //队不为空,则循环deQueue(qu,p); //出队结点pprintf(" %c", p->data); //访问结点pif (p->Ichild!=NULL) enQueue(qu,p->lchild); //有左孩子时将其进队if (p->rchild!=NULL) enQueue(qu,p->rchild); //有右孩子时将其进队}
}
二. 基于递归遍历算法的二叉树有关算法
(1)二叉树的建立
(以先序遍历为例)分两步进行:(1)从键盘输入二叉树的结点信息,建立二叉树的存储结构;(2)在建立二叉树的过程中按照二叉树先序方式建立;

Status CreateBiTree(BiTree &T){ //建立二叉树,传入指针类型scanf(&ch); //从键盘输入,C++中cin>>ch;if(ch == “#”) T=NULL;else{if(!(T=(BiTNode*)malloc(sizeof(BiTNode))))exit(OVERFLOW); //C++中T=new BiTNode;T->data = ch; //生成根结点CreateBiTree(T->Ichild); //构造左子树CreateBiTree(T->rchild); //构造右子树}return OK; //同理,这里return到上一层调用
} //CreateBiTree
这段代码是用来创建二叉树的函数。函数的输入参数是一个指向二叉树根节点的指针T。首先通过scanf函数读取一个字符ch作为输入。如果ch等于"#",表示当前节点为空,将T指向NULL。否则,进入else语句块。在else语句块中,首先通过malloc函数为当前节点分配内存空间,并将分配的地址赋值给T。如果分配内存失败,则程序退出。然后将当前节点的数据域赋值为ch。接下来递归调用CreateBiTree函数,创建当前节点的左子树,将左子树的根节点地址赋值给T->lchild。然后再次递归调用CreateBiTree函数,创建当前节点的右子树,将右子树的根节点地址赋值给T->rchild。最后,函数返回OK表示创建二叉树成功。
利用上面的代码,输入ABC##DE#G##F###,就可建立下面的二叉树链表。

(2)二叉树的复制
int Copy(BiTree T,BiTree &NewT){if(T == NULL){ //如果是空树返回0NewT = NULL;return 0;}else{NewT = new BiTNode; //建立新结点,NewT指针指向它NewT->data = T->data; //传入数据Copy(T->lChild,NewT->lchild); //递归调用,复制左子树Copy(T->rChild,NewT->rchild); //递归调用,复制右子树}
}
这段代码是一个递归函数,用于复制二叉树。函数的参数是原始二叉树T和目标二叉树NewT(通过引用传递),返回值为0表示复制成功。需要注意的是,在函数中使用了引用传递(&)来传递目标二叉树NewT的地址,这是为了能够在函数内部修改目标二叉树NewT的指针,以便将复制得到的子树链接到正确的位置上。
(3)二叉树的深度计算
int Depth(BiTree T){if(T==NULL) return 0; //如果是空树返回0else{m = Depth(T->lChild);n = Depth(T->rChild);if(m>n) return (m+1);else return(n+1);}
}
这段代码是一个递归函数,用于计算二叉树的深度。函数的参数是二叉树T,返回值为二叉树的深度。首先,函数会检查二叉树T是否为空(即是否为叶子节点)。如果是空树,即T为NULL,那么二叉树的深度为0,函数直接返回0。
如果二叉树T不为空,那么函数会递归调用自身,分别计算左子树和右子树的深度,并将结果分别赋值给变量m和n。接下来,函数会比较左子树的深度m和右子树的深度n的大小。如果m大于n,说明左子树更深,那么函数返回m+1,表示整个二叉树的深度为左子树的深度加1。如果n大于等于m,说明右子树更深或者左右子树深度相等,那么函数返回n+1,表示整个二叉树的深度为右子树的深度加1。
最终,当递归调用完成后,函数会返回整个二叉树的深度。
(4)计算二叉树中的结点数
int NodeCount(BiTree T){if(T == NULL)return 0;elsereturn NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}
如果是空树,即T为NULL,那么二叉树中节点的数量为0,函数直接返回0。
如果二叉树T不为空,结点个数=左子树结点数量+右子树结点数量+当前节点(即加1)。
(5)计算二叉树中的叶子结点数
int LeadCount(BiTree T){if(T==NULL) //如果是空树返回0return 0;if (T->Ichild == NULL && T->rchild == NULL)return 1; //如果是叶子结点返回1elsereturn LeafCount(T->lchild) + LeafCount(T->rchild);
}
如果是空树,则叶子结点个数为0;
否则,为左子树的叶子结点个数+右子树的叶子结点个数。
三. 线索二叉树
当用二叉链表作为二叉树的存储结构时,可以很方便地找到某个结点的左右孩子;但一般情况下,无法直接找到该结点在某种遍历序列中的前驱和后继结点。为了解决这个问题,一般有以下解决方案:
- 通过遍历寻找——费时间
- 再增设前驱、后继指针域——增加了存储负担。
- 利用二叉链表中的空指针域。
这里我们重点介绍最后一种。首先回忆下二叉树链表中空指针域的数量:具有n个结点的二叉链表中,一共有2n个指针域(每个结点有左右指针域两个);因为n个结点中有n-1个孩子,即2n个指针域中,有n-1个用来指示结点的左右孩子,其余n+1个指针域为空。
如果某个结点的左孩子为空,则将空的左孩子指针域改为指向其前驱;如果某结点的右孩子为空,则将空的右孩子指针域改为指向其后继。这种改变指向的指针称为“线索",加上了线索的二叉树称为线索二叉树(Threaded Binary Tree)。

为区分lrchid和rchild指针到底是指向孩子的指针,还是指向前驱现白后继的指针,对二叉链表中每个结点增设两个标志域Itag 和rtag,并约定:
- ltag = 0; lchild指向该结点的左孩子;
- ltag = 1; lchild指向该结点的前驱;
- rtag = 0; rchild指向该结点的右孩子;
- rtag = 1; rchild指向该结点的后继;
这样,结点的结构就由5部分组成:

typedef struct BiThrNode{int data;int Itag, rtag;struct BiThrNode *Ichild,*rchild;
}BiThrNode,*BiThrTree;


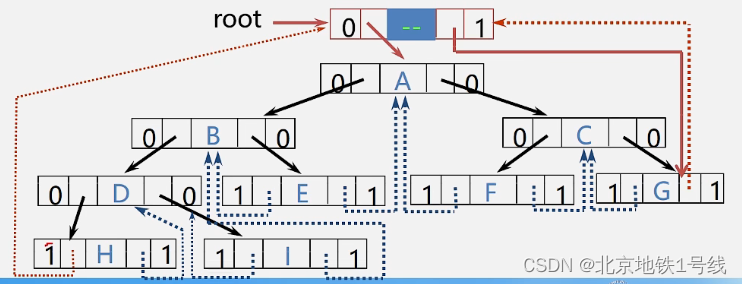
为避免有些指针处于悬空状态,增设了一个头结点,这个头结点还是BiThrNode类型:
ltag=0, lchild指向根结点;
rtag=1, rchild指向遍历序列中最后一个结点;
遍历序列中第一个结点的lc域和最后一个结点的rc域都指向头结点;
这样,改进完的线索二叉树如下:
相关文章:

16.遍历二叉树,线索二叉树
目录 一. 遍历二叉树 (1)三种遍历方式 (2)递归遍历算法 (3)非递归遍历算法 (4)层次遍历算法 二. 基于递归遍历算法的二叉树有关算法 (1)二叉树的建立 …...

电商平台按关键字搜索商品淘宝京东拼多多api接口PHP示例
关键词搜索商品接口的作用是通过调用接口来实现在电商平台中进行商品搜索。具体而言,该接口可以提供以下功能和作用: 商品搜索:用户可以通过输入关键词,在电商平台上进行商品搜索。接口可以根据关键词对商品的名称、描述、标签等…...

胖小酱之恰恰是什么
意思是:指所指的事物截然不同,正好相反。 恰恰相反的近义词:事与愿违、适得其反 一、事与愿违 [ sh yǔ yun wi ] 【解释】:事实与愿望相反。指原来打算做的事没能做到。 【出自】:茅盾《子夜》十六:不…...

豪越科技受邀出席2023中国算力大会
2023年8月17日-8月20日,“算汇银川 数创未来”创新中国行走进银川暨2023中国算力大会在银川中关村创新中心召开。政府领导、行业领袖、专家学者、以及大型科技企业负责人齐聚大会现场,围绕算力基础设施建设、创新应用和产业发展成果等方面开展广泛交流与…...

python脚本——批量将word文件转换成多张图片
前提:有时候需要快速查看word文档的内容是否自己需要的,或者就是单纯需要将word文档转换成一张张图片。 思路:word文档直接生成图片比较蛮烦,可能会引起格式变化,就先将word文档转换成PDF,然后将PDF文档转…...

FairyGUI编辑器的弹窗操作【插件】
之前在FairyGUI编辑器菜单扩展中,我使用了App.Alert("复制失败")来提示操作是否成功。这篇则会说一下我们可以使用的弹窗提示,以及做到类似资源发布成功时的“发布成功”飘窗。 打开APP的API脚本,可以看到有很多公开方法ÿ…...
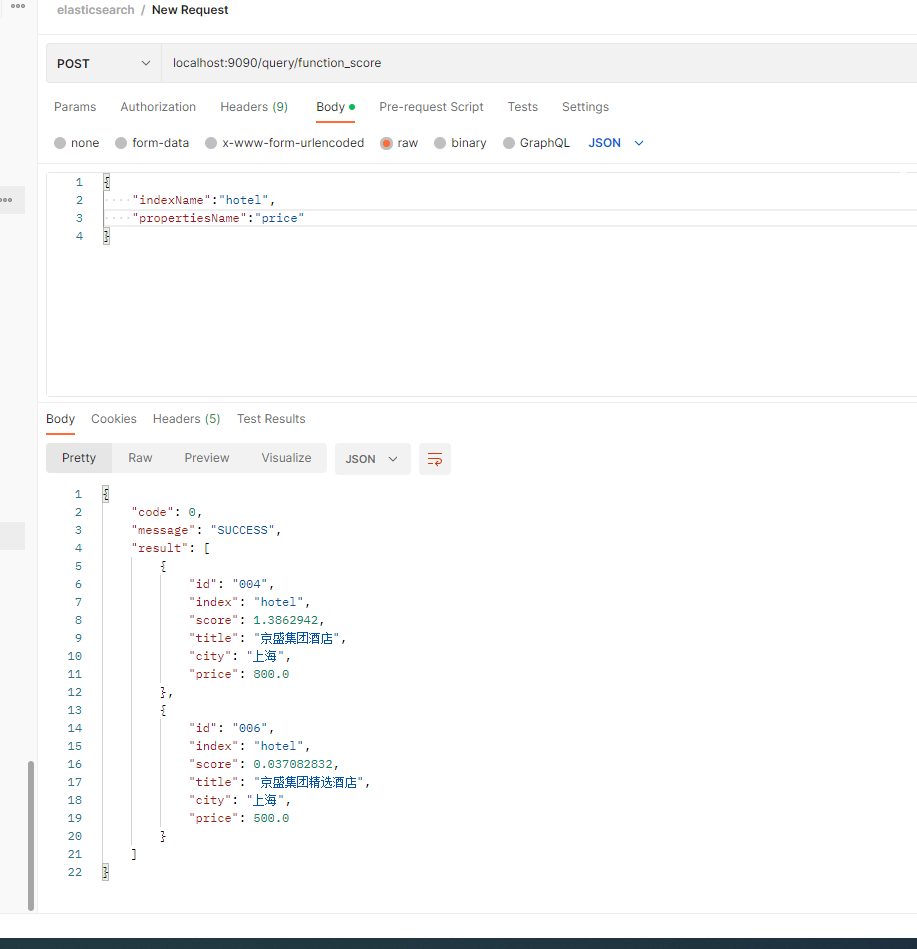
Elasticsearch(十三)搜索---搜索匹配功能④--Constant Score查询、Function Score查询
一、前言 之前我们学习了布尔查询,知道了filter查询只在乎查询条件和文档的匹配程度,但不会根据匹配程度对文档进行打分,而对于must、should这两个布尔查询会对文档进行打分,那如果我想在查询的时候同时不去在乎文档的打分&#…...

直播系统源码协议探索篇(二):网络套接字协议WebSocket
上一篇我们分析了直播平台的会话初始化协议SIP,他关乎着直播平台的实时通信和多方互动技术的实现,今天我们来讲另一个协议,叫网络套接字协议WebSocket,WebSocket基于TCP在客户端与服务器建立双向通信的网络协议,并且可…...
Windows 11 下使用 VMWare Workstation 17 Pro 新建 CentOS Stream 9 64位 虚拟机 并配置网络
文章目录 为什么选择 CentOS Stream 9下载安装访问连接快照克隆网络配置 为什么选择 CentOS Stream 9 CentOS Linux 8: 已经过了 End-of-life (EOL)CentOS Linux 7: EOL Jun 30th, 2024CentOS Stream 8: EOL May 31st, 2024CentOS Stream 9: End of RHEL9 full support phase …...
生信豆芽菜-缺氧评分的计算
网址:http://www.sxdyc.com/gradeHypoxia 1、数据准备 表达谱数据,行为基因,列为样本 2、提交后,等待运行成功即可下载 当然,如果不清楚数据是什么样的,可以选择下载我们的示例数据,也可以…...

C++:通过find/substr分割字符串
find函数可以在一个目标字符串中查找子字符串,返回值为子字符串在目标字符串中的起始位置 substr通过起始位置和长度可以截取一段字符串 将find和substr结合可以用于分割字符串 #include <iostream> #include <string> #include <tuple>using …...
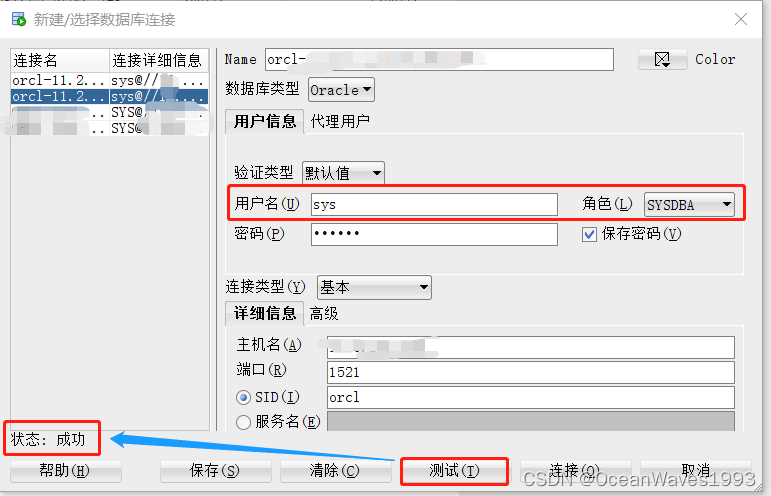
sql developer 连不上oracle数据库 报错 ORA-01031: insufficient privileges
sql developer 连不上oracle数据库 报错 ORA-01031: insufficient privileges 1、问题描述2、问题原因3、解决方法4、sql developer 连接oracle 成功 1、问题描述 使用sys账户以SYSDBA角色登录失败 报错 ORA-01031: insufficient privileges 2、问题原因 因为没有给sys账户分…...

LeetCode 面试题 01.07. 旋转矩阵
文章目录 一、题目二、C# 题解 一、题目 给你一幅由 N N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。 不占用额外内存空间能否做到? 点击此处跳转题目。 示例 1: 给定 matrix [ [1,2,3], [4,5,6], …...
vue3 pdf、word等文件下载
效果: <div class"byLawBox"><div class"titleBox">规章制度公示</div><div class"contentBox"><TableList:loading"byLawloading"ref"byLawtablistRef":hasImport"false"…...
带你了解SpringBoot---开启Durid 监控
文章目录 数据库操作--开启Durid 监控整合Druid 到Spring-Boot官方文档基本介绍Durid 基本使用代码实现 Durid 监控功能-SQL 监控需求:SQL 监控数据SQL 监控数据-测试页面 Durid 监控功能-Web 关联监控需求:Web 关联监控配置-Web 应用、URI 监控重启项目 Durid 监控功能-SQL 防…...

matlab 点云精配准(3)——Trimmed ICP
目录 一、算法原理1、原理概述2、参考文献二、代码实现三、结果展示四、参考链接本文由CSDN点云侠原创,matlab 点云精配准(3)——Trimmed ICP。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 1、原理概述 见论文:[1] 李鑫,莫思特,黄华,…...

nodejs开发环境搭建示例
服务与后端 {"name": "AsaiCC","private": true,"version": "1.0.0","description": "","main": "main.js","bin": "index.js","author": "&…...
网络安全(大厂)面试题
以下为网络安全各个方向涉及的面试题,星数越多代表问题出现的几率越大,祝各位都能找到满意的工作。 注:本套面试题,已整理成pdf文档,但内容还在持续更新中,因为无论如何都不可能覆盖所有的面试问题…...
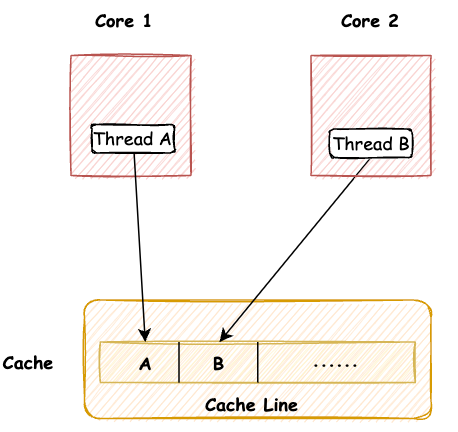
GC面临的困境,JVM是如何解决跨代引用的?
本文已收录至GitHub,推荐阅读 👉 Java随想录 微信公众号:Java随想录 原创不易,注重版权。转载请注明原作者和原文链接 文章目录 跨代引用问题记忆集卡表写屏障写屏障的伪共享问题 前面我们讲了可达性分析和根节点枚举,…...
Qt下拉菜单
1,QComboBox 2,setMenu()---设置下拉菜单 AI对话未来丨智能写作对话: setMenu()是QWidget类的一个成员函数,在Qt中用于将一个菜单作为一个控件的下拉菜单设置。具体来说,它会把相应的菜单对象与该控件关联,并在控件上…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
