统计学作业啊啊啊啊
题目1
一个制药公司宣称其新药可以将病患的恢复时间从10天降至8天。为了验证这一声明,您从服用新药的病患中抽取了一个样本,发现样本均值为9天,样本标准差为2天,样本量为30。使用0.05的显著性水平进行假设检验,判断公司的声明是否成立。
最后的结果可使用Python(scipy库)来完成这个假设检验的计算。
答案
当我们进行假设检验时,尤其是在样本量较小或总体标准差未知的情况下,我们通常使用t分布。t分布与正态分布相似,但其尾部较厚,这是为了修正小样本量导致的估计不确定性。
设置原假设和备择假设:
H 0 : μ = 10 H_0: \mu=10 H0:μ=10 (新药无效)
H 1 : μ < 10 H_1: \mu<10 H1:μ<10 (新药有效)
计算统计量:
t = X ˉ − μ 0 s / n t=\frac{\bar{X}-\mu_0}{s / \sqrt{n}} t=s/nXˉ−μ0
其中, X ˉ \bar{X} Xˉ 是样本均值, μ _ 0 \mu \_0 μ_0 是原假设的总体均值, s s s 是样本标准差, n \mathrm{n} n 是样本量。
t = 9 − 10 2 / 30 = − 1 2 / 30 t=\frac{9-10}{2 / \sqrt{30}}=-\frac{1}{2 / \sqrt{30}} t=2/309−10=−2/301
使用t分布表或相关软件/计算器,查找在显著性水平0.05下,自由度为29的 t \mathrm{t} t 值。如果计算出 的统计量比这个t值还小,则拒绝原假设。如果计算出的t统计量比显著性水平0.05的t值小,则可以拒绝原假设,认为制药公司的声明成立;否则,不能拒绝原假设,说明公司的声明无法得到证实。
具体来说,t分布的形状取决于“自由度”,通常以 d f d f df 表示。对于单样本 t \mathrm{t} t 检验,自由度为 n − 1 n-1 n−1 ,其中 n n n 是 样本量。在上述练习题中,我们的样本量为30,所以自由度是29。 当我们说“在显著性水平0.05下,自由度为29的t值”,我们是在查找一个临界值,这个值将t分布的下5%的区域与上95%的区域分开(因为我们正在进行一个单尾检验,检验μ是否小于10)。 为什么这个临界值如此重要呢? 当我们计算得到一个t统计量,我们需要判断它是否位于t分布的关键区域。如果它在关键区域内(在这种情况下,比临界t值还小,因为我们关心的是左尾),那么我们有足够的证据拒绝原假设。
如果我们的t统计量比这个临界t值还小,那么观察到的样本均值(在这里是9天)与原假设下的总体均值(10天)之间的差异是统计上显著的。因此,我们拒绝原假设,并得出结论:新药的恢复时间确实少于10天。
如果我们的t统计量大于或等于这个临界值,那么我们没有足够的证据拒绝原假设。这并不意味着原假设是正确的,只是意味着我们没有足够的证据证明新药可以缩短恢复时间。
我将使用Python来完成这个假设检验的计算。
首先,我们使用之前提供的信息来计算t统计量:
t = X ˉ − μ 0 s / n t=\frac{\bar{X}-\mu_0}{s / \sqrt{n}} t=s/nXˉ−μ0
其中, X ˉ \bar{X} Xˉ 是样本均值 (9天), μ − 0 \mu_{-} 0 μ−0 是原假设的总体均值(10天), s s s 是样本标准差(2天), n \mathrm{n} n 是样本量 (30)。
接着,我们将使用SciPy库中的 ′ t { }^{\prime} \mathrm{t} ′t 函数来查找自由度为 29 和显著性水平为 0.05 的临界 t t t 值。 最后,我们将比较计算得到的统计量和临界埴,以决定是否拒绝原假设。
让我们开始编写Python代码来完成这些步骤:
import numpy as np
from scipy.stats import t# 给定的数据
sample_mean = 9
population_mean = 10
sample_std = 2
n = 30# 计算t统计量
t_stat = (sample_mean - population_mean) / (sample_std / np.sqrt(n))# 查找显著性水平为0.05和自由度为29的临界t值
t_critical = t.ppf(0.05, df=n-1) # 左尾检验,所以使用0.05print("Calculated t-statistic:", t_stat)
print("Critical t-value for alpha=0.05 and df=29:", t_critical)# 判断是否拒绝原假设
if t_stat < t_critical:print("Reject the null hypothesis: The drug is effective.")
else:print("Fail to reject the null hypothesis: No evidence that the drug is effective.")运行上述代码后,我们可以根据输出结果来判断是否拒绝原假设。
题目2
考虑一个随机实验,每次实验的结果是一个从[0, 1]区间上均匀选择的随机数。令随机变量 X 表示每次实验得到的数值。已知 X 在[0, 1]上是均匀分布的。
求随机变量 X 的期望。
使用积分,计算随机变量 X 的方差。
现在进行该实验1000次,形成一个样本。根据大数定律,样本均值应该接近于什么值?
如果上述实验代表了一个总体,那么再次随机抽取10个样本值,计算其样本均值。你期望这个样本均值与总体均值之间有多大的差异?
答案
-
求随机变量 X X X 的期望。
随机变量 X X X 的期望定义为:
E ( X ) = ∫ a b x f ( x ) d x E(X)=\int_a^b x f(x) d x E(X)=∫abxf(x)dx
由于 X X X 在 [ 0 , 1 ] [0,1] [0,1] 上是均匀分布的,其概率密度函数 f ( x ) f(x) f(x) 是常数,且 f ( x ) = 1 f(x)=1 f(x)=1 (因为该区间 的总概率为1)。
代入上述公式,我们得到:
E ( X ) = ∫ 0 1 x ⋅ 1 d x = ∫ 0 1 x d x = x 2 2 ∣ 0 1 = 1 2 \begin{aligned} & E(X)=\int_0^1 x \cdot 1 d x=\int_0^1 x d x \\ & =\left.\frac{x^2}{2}\right|_0 ^1=\frac{1}{2} \end{aligned} E(X)=∫01x⋅1dx=∫01xdx=2x2 01=21
答案: E ( X ) = 1 2 E(X)=\frac{1}{2} E(X)=21 -
使用积分,计算随机变量 X X X 的方差。
方差定义为:
Var ( X ) = E ( X 2 ) − [ E ( X ) ] 2 \operatorname{Var}(X)=E\left(X^2\right)-[E(X)]^2 Var(X)=E(X2)−[E(X)]2
我们已经知道 E ( X ) = 1 2 E(X)=\frac{1}{2} E(X)=21 。现在,我们需要找到 E ( X 2 ) E\left(X^2\right) E(X2) 。
E ( X 2 ) = ∫ 0 1 x 2 ⋅ 1 d x = ∫ 0 1 x 2 d x = x 3 3 ∣ 0 1 = 1 3 \begin{aligned} & E\left(X^2\right)=\int_0^1 x^2 \cdot 1 d x=\int_0^1 x^2 d x \\ & =\left.\frac{x^3}{3}\right|_0 ^1=\frac{1}{3} \end{aligned} E(X2)=∫01x2⋅1dx=∫01x2dx=3x3 01=31
代入方差的公式,我们得到:
Var ( X ) = 1 3 − ( 1 2 ) 2 = 1 3 − 1 4 = 1 12 \operatorname{Var}(X)=\frac{1}{3}-\left(\frac{1}{2}\right)^2=\frac{1}{3}-\frac{1}{4}=\frac{1}{12} Var(X)=31−(21)2=31−41=121
答案: Var ( X ) = 1 12 \operatorname{Var}(X)=\frac{1}{12} Var(X)=121 -
现在进行该实验 1000 次,形成一个样本。根据大数定律,样本均值应该 接近于什么值?
根据大数定律,随着试验次数的增加,样本均值应该接近于总体均值。在这个例子中,总体 均值是 E ( X ) = 1 2 E(X)=\frac{1}{2} E(X)=21 。
答案: 样本均值应该接近于 1 2 \frac{1}{2} 21 -
如果上述实验代表了一个总体,那么再次随机抽取10个样本值,计算其 样本均值。你期望这个样本均值与总体均值之间有多大的差异?
由于这是一个随机实验,我们不能预先知道确切的差异。但我们可以计算标准误差来估计差 异的大小。
标准误差定义为:
S E = σ n S E=\frac{\sigma}{\sqrt{n}} SE=nσ
其中, σ \sigma σ 是总体标准差,而 n \mathrm{n} n 是样本大小。在这里, σ = Var ( X ) = 1 12 \sigma=\sqrt{\operatorname{Var}(X)}=\sqrt{\frac{1}{12}} σ=Var(X)=121 且 n = 10 \mathrm{n}=10 n=10 。
S E = 1 12 10 S E=\frac{\sqrt{\frac{1}{12}}}{\sqrt{10}} SE=10121
这个值给出了样本均值的平均波动幅度。
答案: 我们期望样本均值与总体均值之间的差异大约在上述的标准误差范围内。
相关文章:

统计学作业啊啊啊啊
题目1 一个制药公司宣称其新药可以将病患的恢复时间从10天降至8天。为了验证这一声明,您从服用新药的病患中抽取了一个样本,发现样本均值为9天,样本标准差为2天,样本量为30。使用0.05的显著性水平进行假设检验,判断公…...

CAM实现的流程--基于Pytorch实现
CAM实现的流程 CAM类激活映射CAM是什么CAM与CNN CAM类激活映射 CAM是什么 可视化CNN的工具, CAM解释网络特征变化,CAM使得弱监督学习发展成为可能,可以慢慢减少对人工标注的依赖,能降低网络训练的成本。通过可视化,就…...
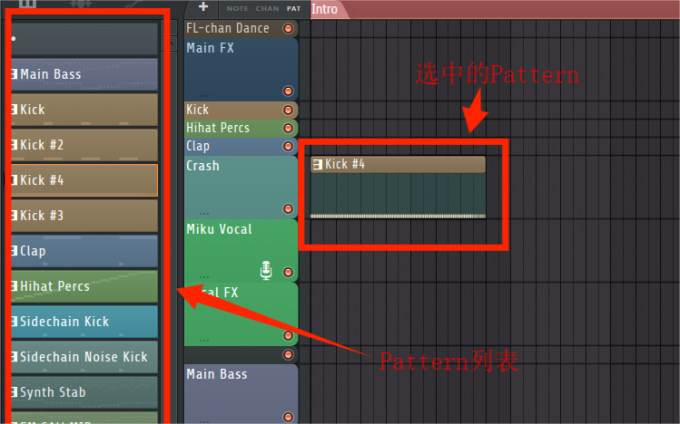
FL Studio2023最新版本21.1中文水果音乐编曲工具
虚拟乐器和真实乐器的区别?真实乐器指的是现实中需要乐手演奏的乐器,而虚拟乐器是计算机音乐制作中编曲师使用的数字乐器。FL Studio虚拟乐器插件有哪些?下文将给大家介绍几款FL Studio自带的强大虚拟乐器。 一、虚拟乐器和真实乐器的区别 …...

数据库概述SQL基本语法
基本概念 数据库DB database简称DB: 存储数据的仓库,是以某种结构存储数据的文件。指长期保存在计算机的存储设备上,按照一定规则阻止起来,可以被用户或应用共享的数据集合。 数据库管理系统DBMS 用于创建,维护,使…...

【面试】一文讲清组合逻辑中的竞争与冒险
竞争的定义:组合逻辑电路中,输入信号的变化传输到电路的各级逻辑门,到达的时间有先后,也就是存在时差,称为竞争。 冒险的定义:当输入信号变化时,由于存在时差,在输出端产生错误&…...

无涯教程-PHP - 性能优化
根据Zend小组的说明,以下插图显示了PHP 7与PHP 5.6和基于流行的基于PHP的应用程序上的HHVM 3.7。 Magento 1.9 与执行Magento事务的PHP 5.6相比,PHP 7的运行速度证明是其两倍。 Drupal 7 在执行Drupal事务时,与PHP 5.6相比,PHP 7的运行速度…...

如何在PHP中使用字符串
引言 字符串是由一个或多个字符组成的序列,可以由字母、数字或符号组成。所有的书面通信都是由字符串组成的。因此,它们是任何编程语言的基础。 在本文中,您将学习如何创建和查看字符串的输出,如何使用转义序列,如何连…...

Mybatis简单入门
星光下的赶路人star的个人主页 夏天就是吹拂着不可预期的风 文章目录 1、Mybatis介绍1.1 JDBC痛点1.2 程序员的诉求1.3 Mybatis简介 2、数据准备2.1 数据准备2.2 建工程2.3 Employee类2.4 Mybatis的全局配置2.5 编写要执行的SQL2.6 编写java程序2.7 稍微总结一下流程 3、解决属…...
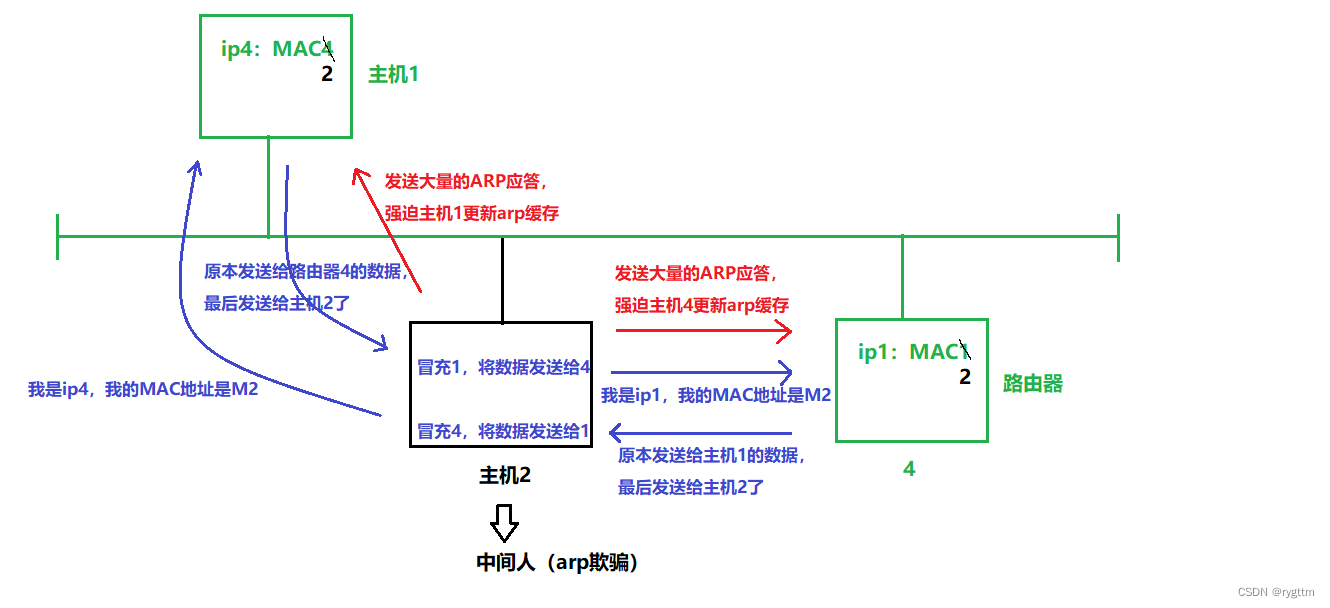
【Linux】数据链路层:以太网协议
约束不等于压迫,冷静和理性不等于冷淡和麻木。 文章目录 一、以太网帧 和 局域网转发数据包1.局域网转发的原理(基于以太网协议)2.以太网MTU与MAC地址 二、局域网中的数据碰撞1.如何解决局域网中的数据碰撞?(碰撞检测和…...
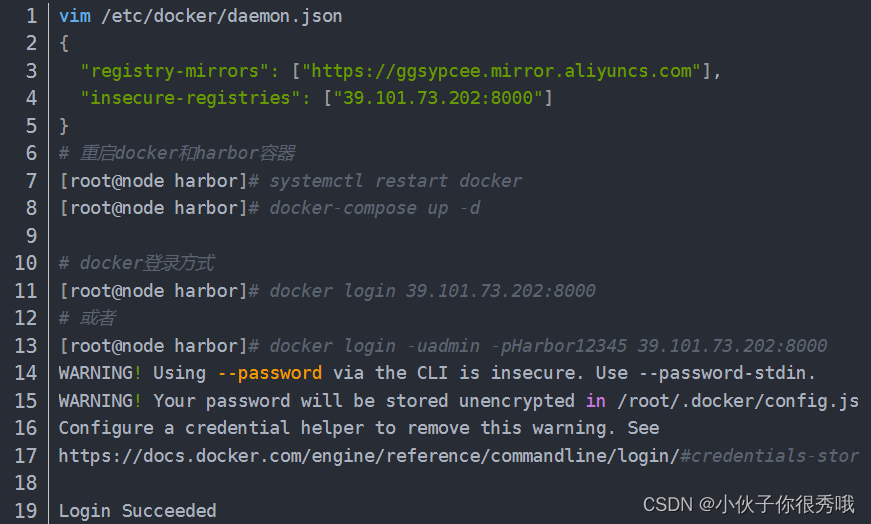
docker搭建私有镜像harbor
docker安装搭建私有仓库 Harbor harbor用于存储和分布docker镜像企业级registry服务器的harbor使用的是官方的docker registry(v2命名是distribution)服务去完成。 安装harhor 启动harbor 6....

汽车便携轮胎充气泵方案
便携式充气泵是一种小巧便捷的充气工具,可广泛应用于汽车、自行车、摩托车、游泳圈、球类等充气产品的充气过程中。该产品以其小巧轻便、充气效率高、操作简单等特点备受消费者的青睐。 充气泵工作过程 当电动机启动时,通过电磁离合器将气泵内的活塞带动…...
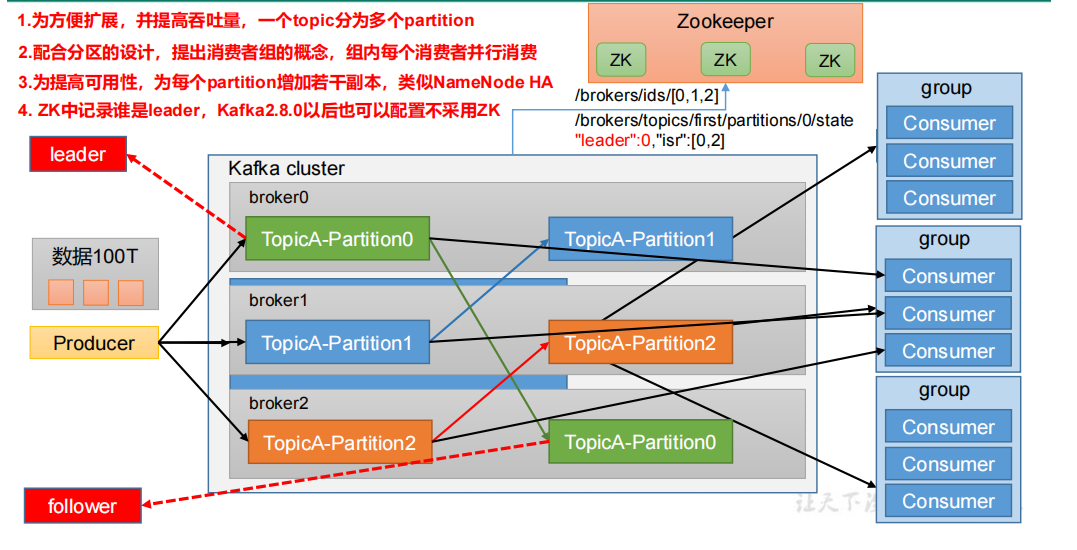
一、Kafka概述
目录 1.3 Kafka的基础架构 1.3 Kafka的基础架构 Producer:消息生产者,就是向 Kafka broker 发消息的客户端Consumer:消息消费者,向 Kafka broker 取消息的客户端。Consumer Group(CG):消费者组&…...
【数据结构OJ题】合并两个有序链表
原题链接:https://leetcode.cn/problems/merge-two-sorted-lists/description/ 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 可以先创建一个空链表,然后依次从两个有序链表中选取最小的进行尾插操作。(有点类似双…...

C++ LibCurl 库的使用方法
LibCurl是一个开源的免费的多协议数据传输开源库,该框架具备跨平台性,开源免费,并提供了包括HTTP、FTP、SMTP、POP3等协议的功能,使用libcurl可以方便地进行网络数据传输操作,如发送HTTP请求、下载文件、发送电子邮件等…...
-[向量存储器(Vectorstores)])
自然语言处理从入门到应用——LangChain:索引(Indexes)-[向量存储器(Vectorstores)]
分类目录:《自然语言处理从入门到应用》总目录 Vectorstores是构建索引的最重要组件之一。本文展示了与VectorStores相关的基本功能。在使用VectorStores时,创建要放入其中的向量是一个关键部分,通常通过嵌入来创建。 from langchain.embedd…...
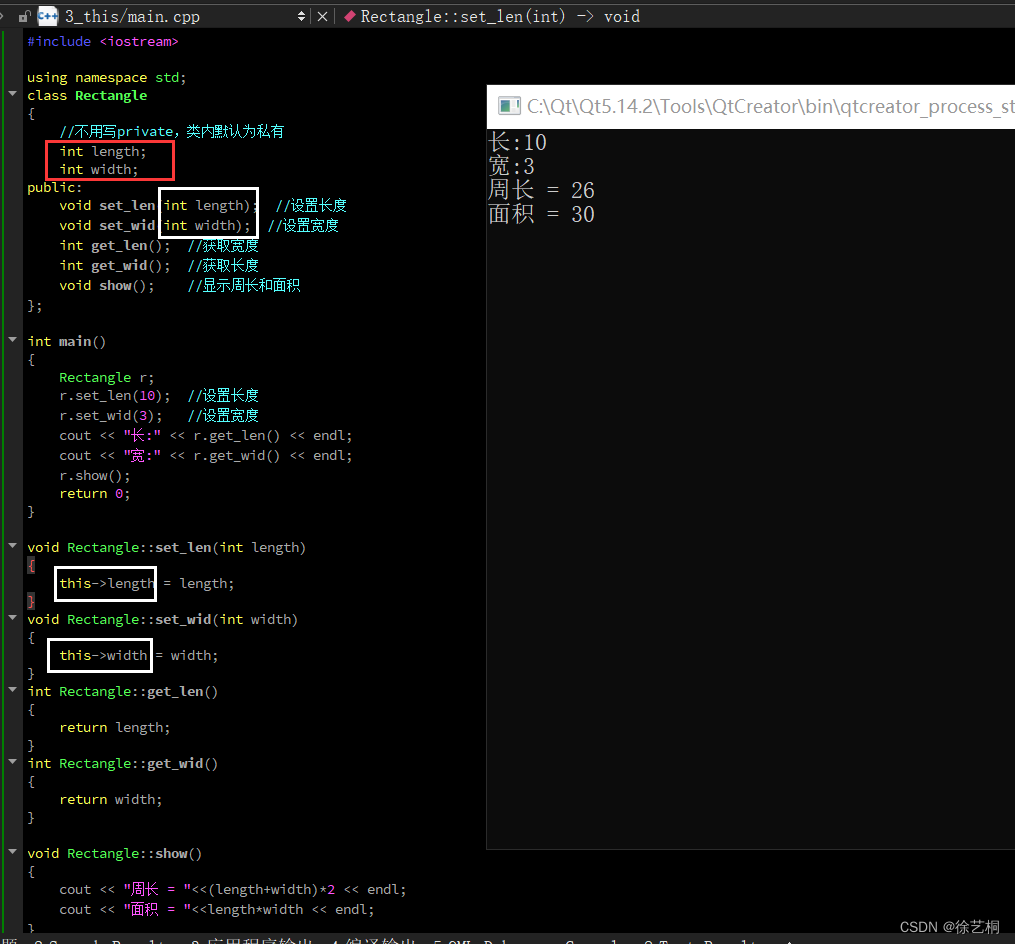
【C++练习】普通方法+利用this 设置一个矩形类(Rectangle), 包含私有成员长(length)、 宽(width), 定义一下成员函数
题目 设置一个矩形类(Rectangle), 包含私有成员长(length)、 宽(width), 定义成员函数: void set_ len(int l); //设置长度 设置宽度void set_ wid(int w); 获取长度: int get len(); 获取宽度: int get _wid); 显示周长和面积: v…...
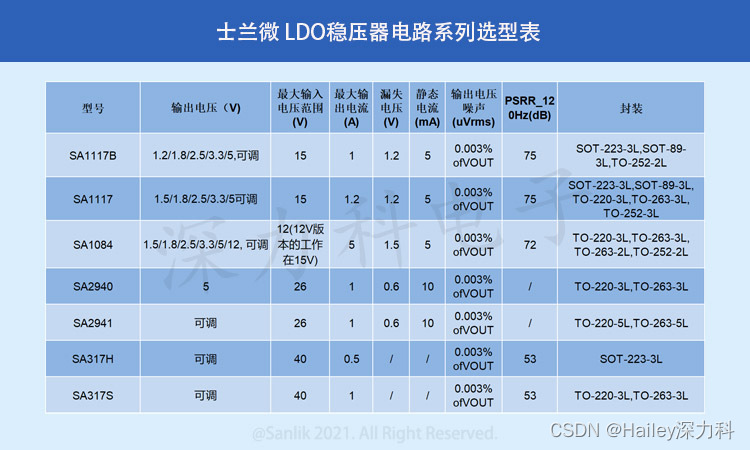
电子电路学习笔记之SA1117BH-1.2TR——LDO低压差线性稳压器
关于LDO调节器(Low Dropout Regulator)是一种电压稳压器件,常用于电子设备中,用于将高电压转换为稳定的低电压。它能够在输入电压和输出电压之间产生较小的差异电压,因此被称为"低压差稳压器"。 LDO调节器通…...

【LeetCode-面试经典150题-day7】
392.判断子序列 题意: 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是&quo…...
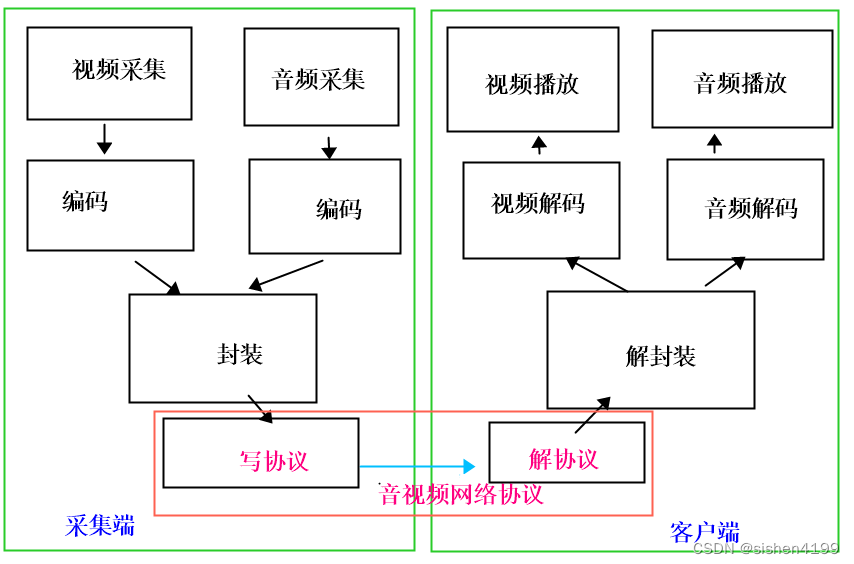
00-音视频-概述
有很多场合会使用的音视频,比如安防、视频闸机、影音播放器、视频通话,短视频等等。 从摄像头采集到用户观看,这中间涉及到了很多技术。 用户一般观看的高清视频1080P30帧。若按24位RGB对视频进行存储,一个60分钟视频所占空间 …...

SOFARPC(笔记)
文章目录 一、快速开始1.1 SOFARPC1.2 基于SOFABoot 二、注册中心三、通讯协议2.1 Bolt基本发布调用方式超时控制协议泛化调用序列化协议自定义线程池 2.2 RESTful基本使用 2.3 其他协议四、架构 附录 官方样例下载地址-sofa-boot-guides 可查看 SOFARPC 方式快速入门 一、快…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
