利用OpenCV的函数equalizeHist()对图像作直方图均衡化处理
如果一幅图像的灰度值集中在某个比较窄的区域,则图像的对比度会显得比较小,不便于对图像的分析和处理。
图像的直方图均衡化可以实现将原图像的灰度值范围扩大,这样图像的对比度就得到了提高,从而方便对图像进行后续的分析和处理。
文字说明比较抽象,对于图像的直方图均衡化,大家看下面的两幅截图会有更直观的认识。
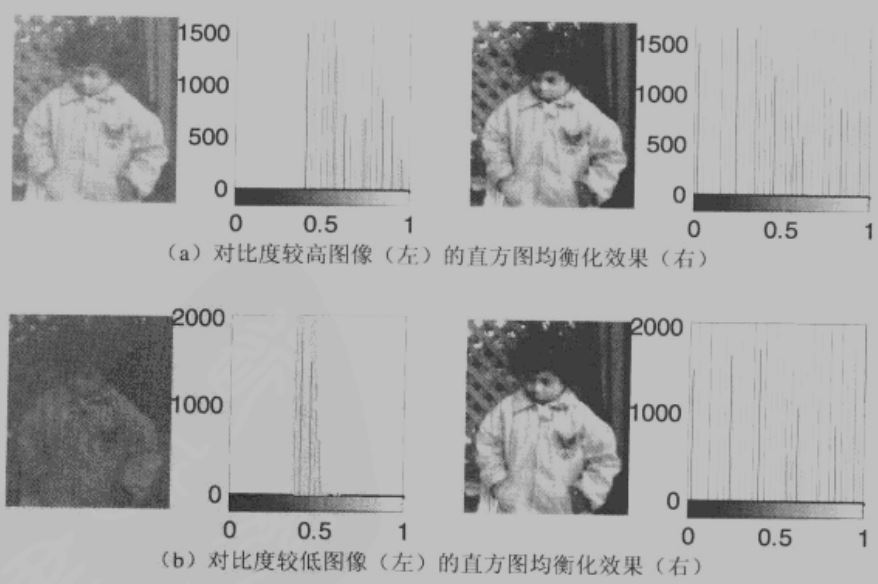
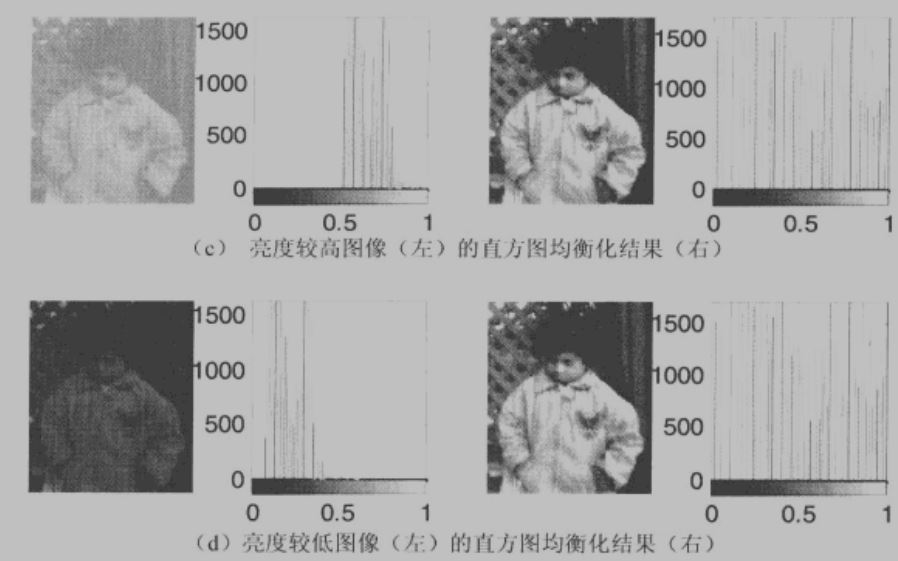
从上面两幅的截图中我们发现,将直方图均衡化算法应用于左侧亮图、对比度不同的各个图像后,得到了右侧直方图大致相同的图像,这体现了直方图均衡化在图像增强方面的自适应性。
当原始图像的直方图不同而图像结构性内容相同时,直方图均衡化所得到的结果在视觉上几乎是完全于致的。这样的处理效果对于在进行图像分析和比较之前将图像转化为统一的形式是十分有益。
算法原理如下:
⑴根据原图像的灰度累计分布构建重映射表;
⑵通过重映射表,对原图像进行重映射,得到经直方图均衡化后的图像。
具体的算法实现步骤如下:
⑴统计图像中各灰度级的出现次数,存储在大小为256的数组hist_sz中,比如 hist_sz[200]=2 代表灰度值为200的像素点出现次数为2。
⑵初始化图像直方图均衡化映射表数组lut中,比如 lut[200]=204 代表把原图像灰度值为200的像素的灰度值重新映射为204。
⑶建立映射表,具体方法如下:
这里以求灰度值3映射为多少灰度值为例说明这个问题。
①统计小于等于某一级的像素的点有多少个,并存储于变量sum中。比如灰度值小于等于2的像素点的个数有8个,灰度值为3的像素点个数有3个,则灰度值小于等于3的像素点个数为8+3=11(个),此时sum变量的值为11。
②利用下面两个语句计算得到映射目标值,并将映射目标值存储在数组lut中:
scale=255/(heightwidth);
val=sumscale;
③利用存储在lut数组中的映射表把源图像的像素值作一个新的映射,例如语句“dst(y,x)=lut(1,src_y_x);”。
从上面具体的实现过程,我们可以看出,均衡化实际上就是按图像灰度值的出现频率去重新调整整幅图的灰度值,这样就使得对比度不同但内容相同的图像看起来一致了。
OpnCV提供了函数equalizeHist()对图像进行直方图均衡化。
函数equalizeHist()的原型如下:
void cv::equalizeHist(InputArray src,OutputArray dst )
函数equalizeHist()的使用示例代码如下:
代码中用到的图片的下载链接请访问本博文的原文获取,
本博文的原文链接如下:
https://www.hhai.cc/thread-218-1-1.html
//出处:昊虹AI笔记网(hhai.cc)
//用心记录计算机视觉和AI技术//博主微信/QQ 2487872782
//QQ群 271891601
//欢迎技术交流与咨询//OpenCV版本 OpenCV3.0#include <opencv2/opencv.hpp>
#include <iostream>using namespace std;
using namespace cv;int main()
{cv::Mat srcImage = cv::imread("E:/material/images/2023/2023-01/he01.png", 0);if( !srcImage.data ) return 1;cv::imshow("srcImage", srcImage);// 直方图均衡化cv::Mat heqResult;cv::equalizeHist(srcImage, heqResult);cv::imshow("heqResult", heqResult);cv::waitKey(0);return 0;
}
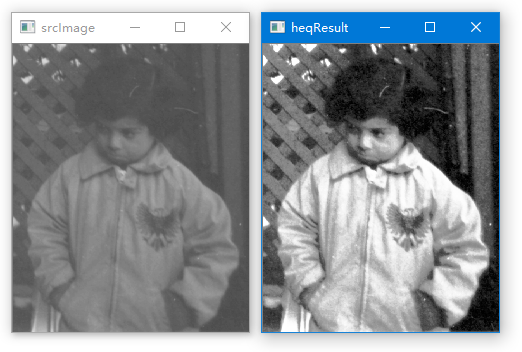
运行结果如下:
相关文章:

利用OpenCV的函数equalizeHist()对图像作直方图均衡化处理
如果一幅图像的灰度值集中在某个比较窄的区域,则图像的对比度会显得比较小,不便于对图像的分析和处理。 图像的直方图均衡化可以实现将原图像的灰度值范围扩大,这样图像的对比度就得到了提高,从而方便对图像进行后续的分析和处理…...

星河智联Android开发
背景:朋友内推,过了一周约面。本人 2019年毕业 20230208一面 1.自我介绍 2.为啥换工作 3.项目经历(中控面板、智能音箱、语音问的比较细) 4.问题 Handler机制原理?了解同步和异步消息吗?View事件分发…...

【C++】关联式容器——map和set的使用
文章目录一、关联式容器二、键值对三、树形结构的关联式容器1.set2.multiset3.map4.multimap四、题目练习一、关联式容器 序列式容器📕:已经接触过STL中的部分容器,比如:vector、list、deque、forward_list(C11)等,这些容器统称为…...

Promise的实现原理
作用:异步问题同步化解决方案,解决回调地狱、链式操作原理: 状态:pending、fufilled reject构造函数传入一个函数,resolve进入then,reject进入catch静态方法:resolve reject all any react ne…...
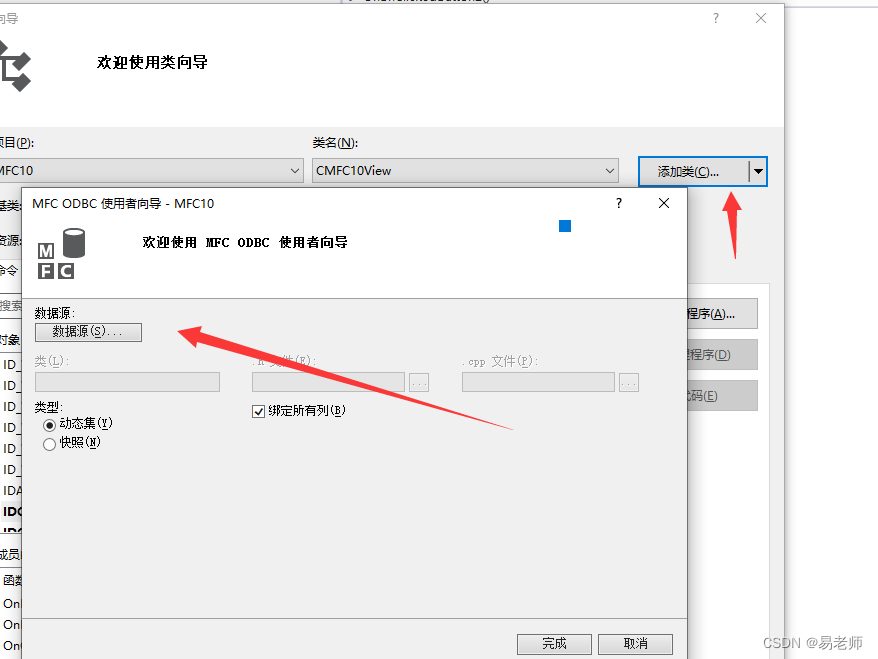
【MFC】数据库操作——ODBC(20)
ODBC:开放式数据库连接,是为解决异构数据库(不同数据库采用的数据存储方法不同)共享而产生的。ODBC API相对来说非常复杂,这里介绍MFC的ODBC类。 添加ODBC用户DSN 首先,在计算机中添加用户DSN:(WIN10下&a…...
旺店通与金蝶云星空对接集成采购入库单接口
旺店通旗舰奇门与金蝶云星空对接集成采购入库单查询连通销售退货新增V1(12-采购入库单集成方案-P)数据源系统:旺店通旗舰奇门旺店通是北京掌上先机网络科技有限公司旗下品牌,国内的零售云服务提供商,基于云计算SaaS服务模式,以体系化解决方案…...
Linux基础-学会使用命令帮助
概述使用 whatis使用 man查看命令程序路径 which总结参考资料概述Linux 命令及其参数繁多,大多数人都是无法记住全部功能和具体参数意思的。在 linux 终端,面对命令不知道怎么用,或不记得命令的拼写及参数时,我们需要求助于系统的…...
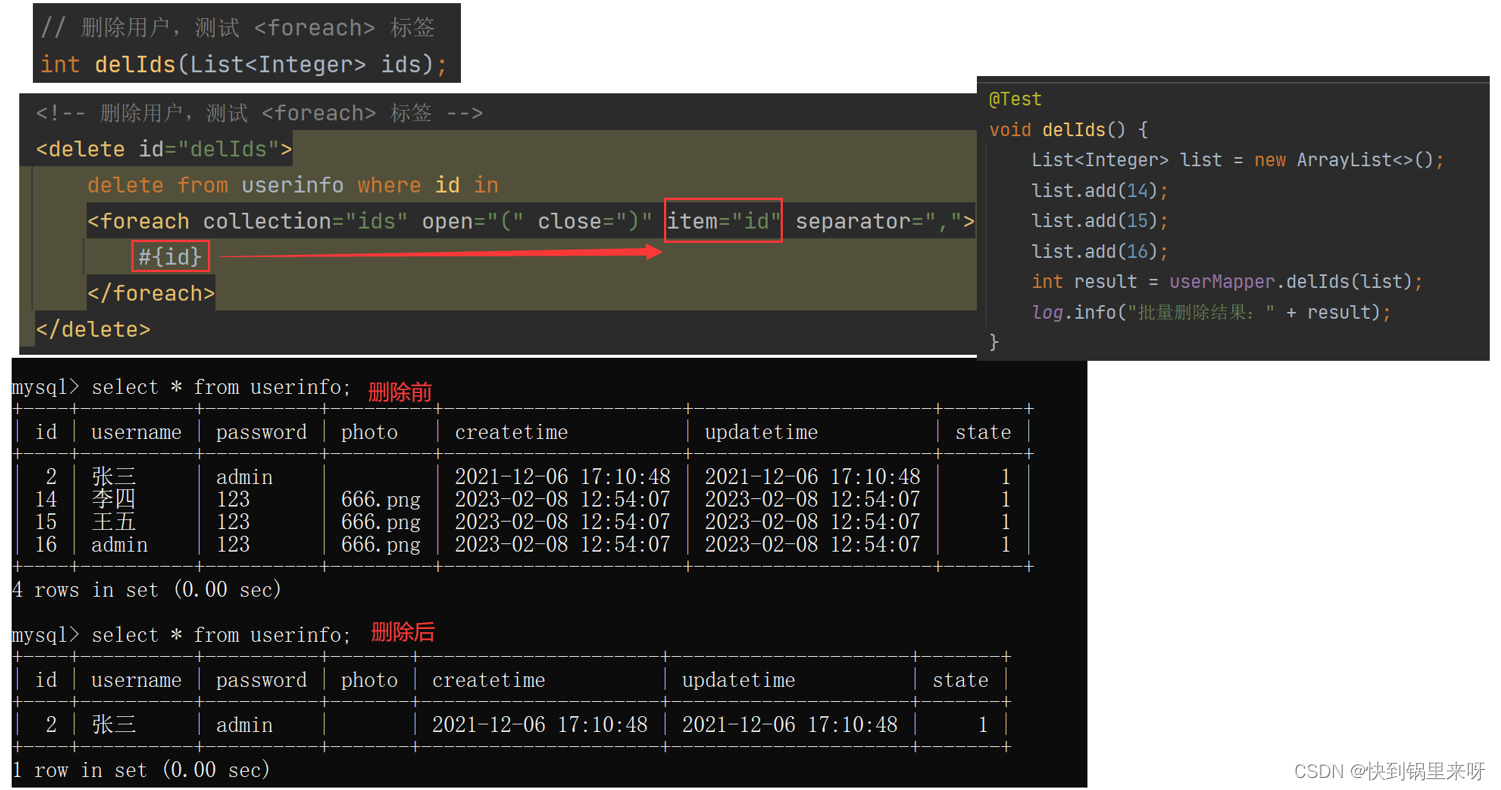
MyBatis 之四(动态SQL之 if、trim、where、set、foreach 标签)
文章目录动态 SQL1. if 标签2. trim 标签3. where 标签4. set 标签5. foreach 标签回顾一下,在上一篇 MyBatis 之三(查询操作 占位符#{} 与 ${}、like查询、resultMap、association、collection)中,学习了针对查询操作的相关知识点…...
 Practice 1006 Sign In and Sign Out)
PAT (Advanced Level) Practice 1006 Sign In and Sign Out
1006 Sign In and Sign Out题目翻译代码分数 25作者 CHEN, Yue单位 浙江大学At the beginning of every day, the first person who signs in the computer room will unlock the door, and the last one who signs out will lock the door. Given the records of signing in’…...

Android入门第64天-MVVM下瀑布流界面的完美实现-使用RecyclerView
前言 网上充满着不完善的基于RecyclerView的瀑布流实现,要么根本是错的、要么就是只知其一不知其二、要么就是一充诉了一堆无用代码、要么用的是古老的MVC设计模式。 一个真正的、用户体验类似于淘宝、抖音的瀑布流怎么实现目前基本为无解。因为本人正好自己空闲时也…...
Windows PowerShell中成功进入conda虚拟环境
本人操作系统是Windows10(输入命令cmd或在运运行中输入winver查看)在cmd命令行中大家都很熟悉,很方便进入到指定创建了的虚拟环境中,那么在PowerShell中怎么进入呢?比如在VSCode中的TERMINAL使用的是PowerShell&#x…...

【C++】类与对象理解和学习(中)
专栏放在【C知识总结】,会持续更新,期待支持🌹六大默认成员函数前言每个类中都含有六大默认成员函数,也就是说,即使这个类是个空类,里面什么都没有写,但是编译器依然会自动生成六个默认成员函数…...
大英复习单词和翻译)
每日英语学习(11)大英复习单词和翻译
2023.2.20 单词 1.contemplate 思考、沉思 2.spark 激起 3.venture 冒险 4.stunning 极好的 5.dictate 影响 6.diplomatic 外交的 7.vicious 恶性的 8.premier 首要的 9.endeavor 努力 10.bypass 绕过 11.handicaps 不利因素 12.vulnerable 脆弱的 13.temperament 气质、性格…...

x79主板M.2无法识别固态硬盘
问题描述: 这几天在装电脑,买了块M.2接口固态硬盘。装上去始终无法读取到硬盘,一开始以为是寨板Bios问题不支持M.2的设备。更新了最新的BIOS然后还是没有识别出来,然而将日常用的电脑PM510硬盘装上发现可以识别,而且日常用电脑也…...

配置Tomcat性能优化
配置Tomcat性能优化 📒博客主页: 微笑的段嘉许博客主页 💻微信公众号:微笑的段嘉许 🎉欢迎关注🔎点赞👍收藏⭐留言📝 📌本文由微笑的段嘉许原创! Ǵ…...
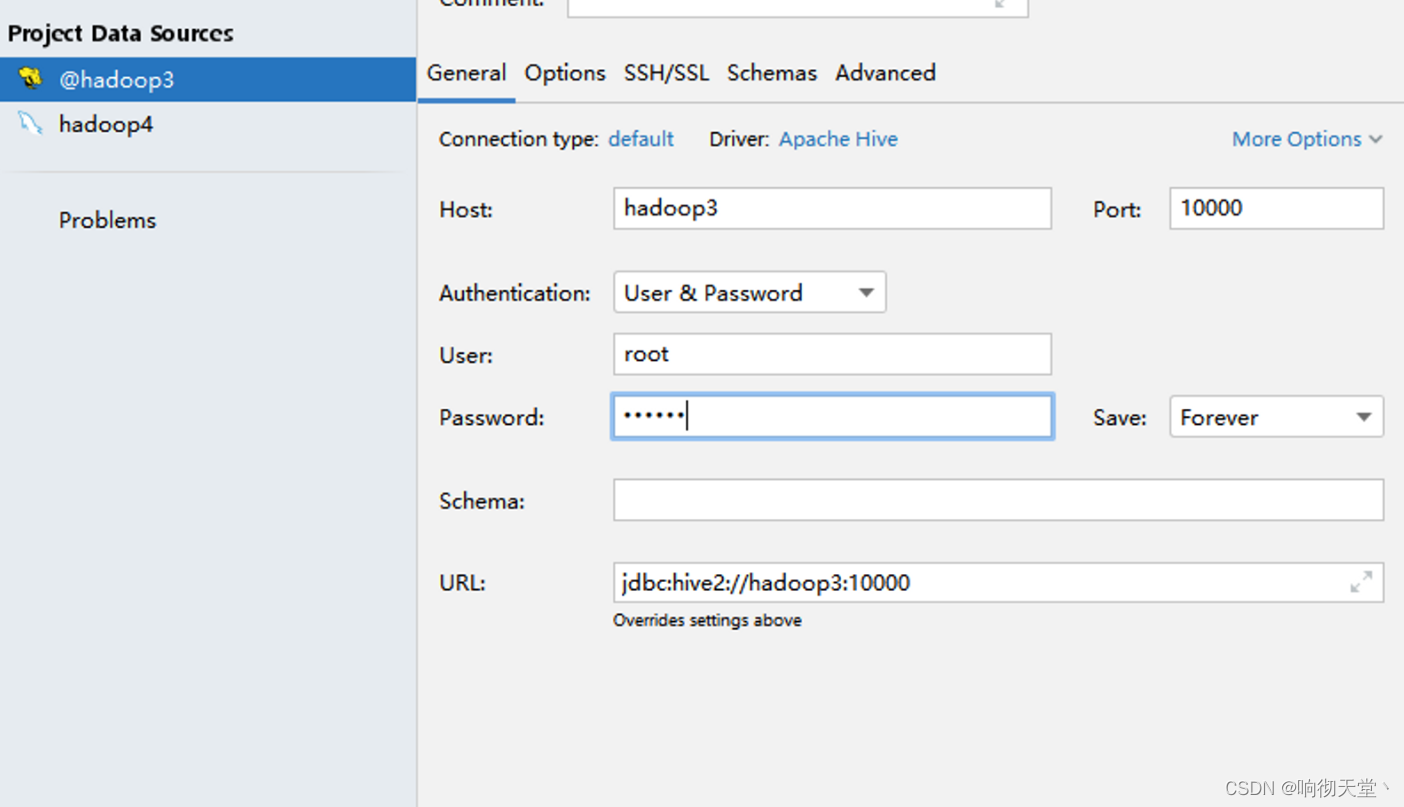
Hive3 安装方式详解,datagrid自定义驱动连接hive
1 Hive的安装方式 hive的安装一共有三种方式:内嵌模式、本地模式、远程模式。 元数据服务(metastore)作用是:客户端连接metastore服务,metastore再去连接MySQL数据库来存取元数据。有了metastore服务,就可以有多个客户端同时连接…...
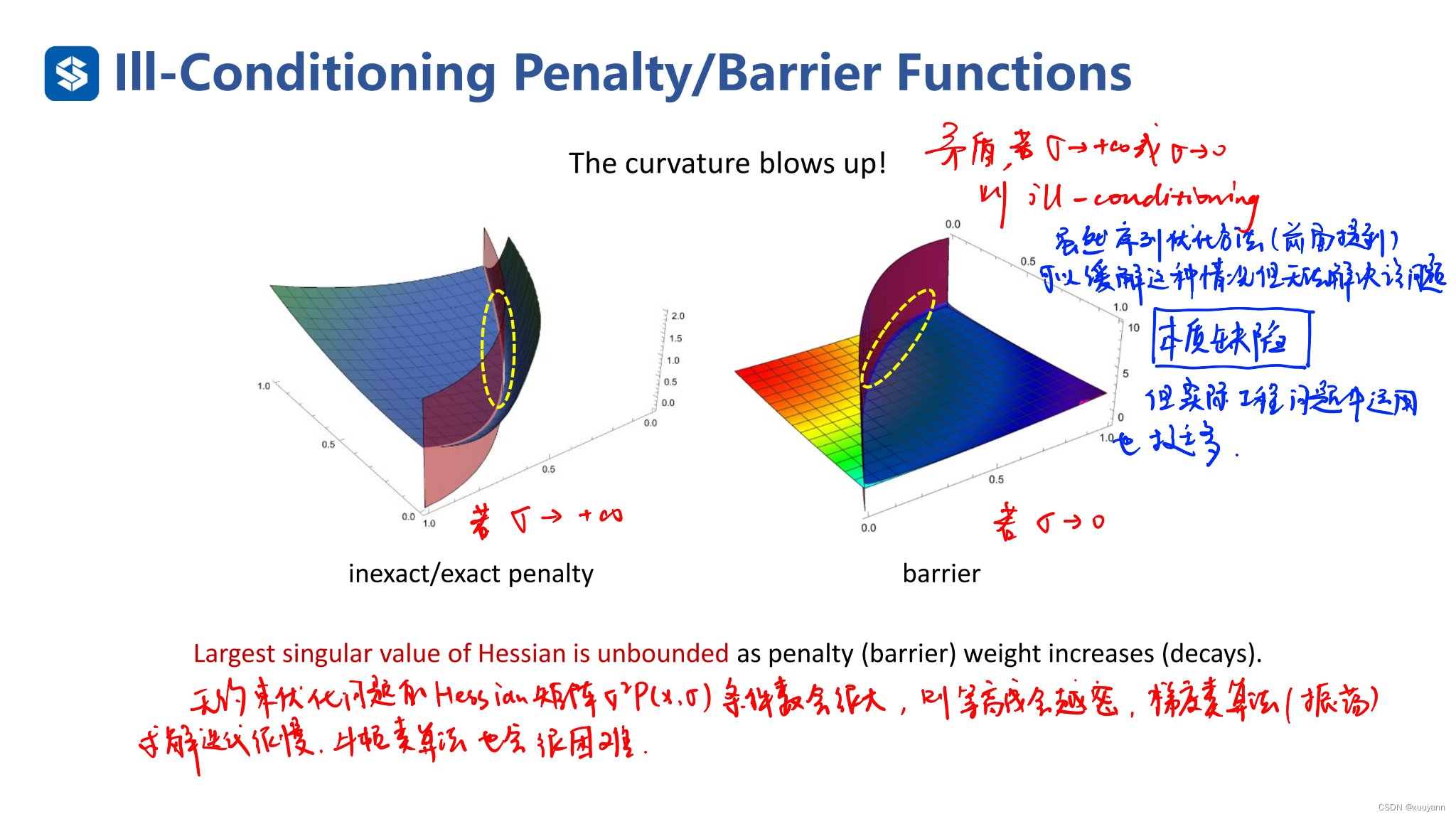
约束优化:约束优化的三种序列无约束优化方法(罚函数法)
文章目录约束优化:约束优化的三种序列无约束优化方法(罚函数法)外点罚函数法L2-罚函数法:非精确算法对于等式约束对于不等式约束L1-罚函数法:精确算法内点罚函数法:障碍函数法参考文献约束优化:…...

你真的会做APP UI自动化测试吗?我敢打赌百分之九十的人都不知道这个思路
目录 前言 一,开发语言选择 二,UI测试框架选择 1,Appium 2,Airtest 3,选择框架 三,单元测试框架选择 四,测试环境搭建 1,测试电脑选择 2,测试手机选择 3&#…...
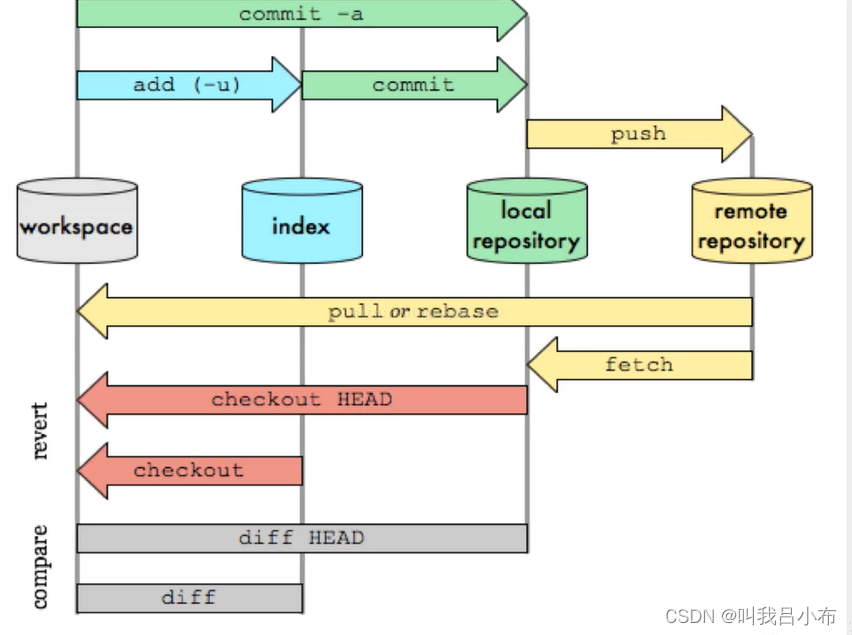
GIT:【基础三】Git工作核心原理
目录 一、Git本地四个工作区域 二、Git提交文件流程 一、Git本地四个工作区域 工作目录(Working Directory):电脑上存放开发代码的地方。暂存区(Stage/Index):用于l临时存放改动的文件,本质上只是一个文件,保存即将提交到文件列…...

【1.12 golang中的指针】
1. 指针 区别于C/C中的指针,Go语言中的指针不能进行偏移和运算,是安全指针。 要搞明白Go语言中的指针需要先知道3个概念:指针地址、指针类型和指针取值。 1.1. Go语言中的指针 Go语言中的函数传参都是值拷贝,当我们想要修改某…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
