Python之Qt输出UI
安装PySide2

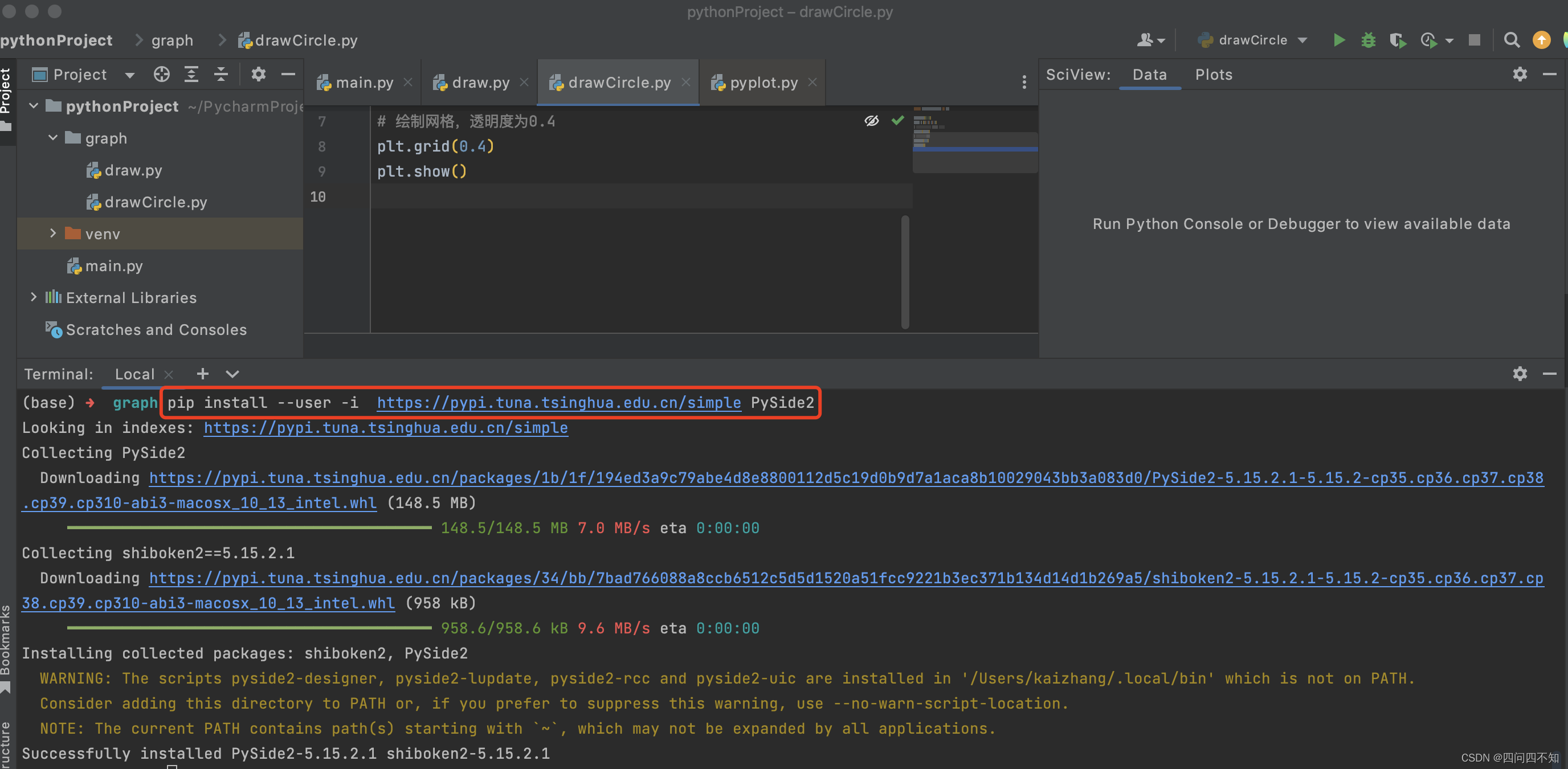
输入pip install PySide2安装Qt for Python,如果安装过慢需要翻墙,则可以使用国内清华镜像下载,输入命令pip install --user -i https://pypi.tuna.tsinghua.edu.cn/simple PySide2,如下图,
示例Demo
import random
import sysfrom PySide2 import QtCore, QtWidgets, QtGuiclass MyWidget(QtWidgets.QWidget):def __init__(self):super().__init__()self.hello = ["您已点击1次", "您已点击2次", "您已点击3次", "您已点击4次"]self.button = QtWidgets.QPushButton("请点击按钮")self.text = QtWidgets.QLabel("测试用户界面")self.text.setAlignment(QtCore.Qt.AlignCenter)self.layout = QtWidgets.QVBoxLayout()self.layout.addWidget(self.text)self.layout.addWidget(self.button)self.setLayout(self.layout)self.button.clicked.connect(self.magic)def magic(self):self.text.setText(random.choice(self.hello))if __name__ == "__main__":app = QtWidgets.QApplication([])widget = MyWidget()widget.resize(600, 400)widget.show()sys.exit(app.exec_())
可能报错如下,
Class QMacAutoReleasePoolTracker is implemented in both xxx and xxx. One of the two will be used. Which one is undefined.
该原因是mac版本下安装的opencv包包含一些qt的头文件与PyQt5冲突了,导致无法正确导入相应的包。
输入命令pip uninstall xxx卸载掉冲突的包即可。最后输出UI界面。
相关文章:

Python之Qt输出UI
安装PySide2 输入pip install PySide2安装Qt for Python,如果安装过慢需要翻墙,则可以使用国内清华镜像下载,输入命令pip install --user -i https://pypi.tuna.tsinghua.edu.cn/simple PySide2,如下图, 示例Demo i…...

【1day】复现泛微OA某版本SQL注入漏洞
目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现 一、漏洞描述 泛微e-cology是一款由泛微网络科技开发的协同管理平台,支持人力资源、财务、行政等多功能管理和移动办公。泛微OA存在SQL注入漏洞,攻击者利用Web应用程序对用户输入验证上的疏忽,在输入的数据…...
安卓系列机型-禁止卸载某个APP 防止误卸载软件 无需root权限
安卓系列机型-禁止安装某软件 防止“沉迷游戏的小孩”操作解析_安卓机器的博客-CSDN博客 上一期讲了如何禁止安装某个app。今天讲下如何禁止卸载某app。正好相反的操作。任何操作有利有弊。主要看使用者如何对待使用。 💔💔💔以腾讯的一款游…...
【算法系列篇】二分查找——这还是你所知道的二分查找算法吗?
文章目录 前言什么是二分查找算法1.二分查找1.1 题目要求1.2 做题思路1.3 Java代码实现 2.在排序数组中查找元素的第一个和最后一个位置2.1 题目要求2.2 做题思路2.3 Java代码实现 3.搜索插入位置3.1 题目要求3.2 做题思路3.3 Java代码实现 4.x的平方根4.1 题目要求4.2 做题思路…...

【前端从0开始】JavaSript——分支流程控制
流程控制 在任何一门程序设计语言中,都需要支持满足程序结构 化所需要的三种流程控制: ●顺序控制 ●分支控制(条件控制) ●循环控制 顺序控制:在程序流程控制中,最基本的就是顺序控制。程序会按照自上而下的顺序执行…...
Linux权限
Linux中一切皆文件,那么文件就应该有相对于的类型,而在Linux当中,类型不是直接看后缀来决定的。 -普通文件、文本、可执行、归档文件等d目录b块设备、block、磁盘c字符设备、键盘、显示器p管道文件s网络socket文件l链接文件 link 然后后面的九…...

PMP如何备考?学习方式这里有
预习阶段:强烈建议跟着习课视频学习(自己看书真的很难看懂),初步了解PMBOK,有个大致印象; 精讲阶段:这个时候就需要静下心来深入了解各个知识模块,不仅是看PMBOK,还要尽…...
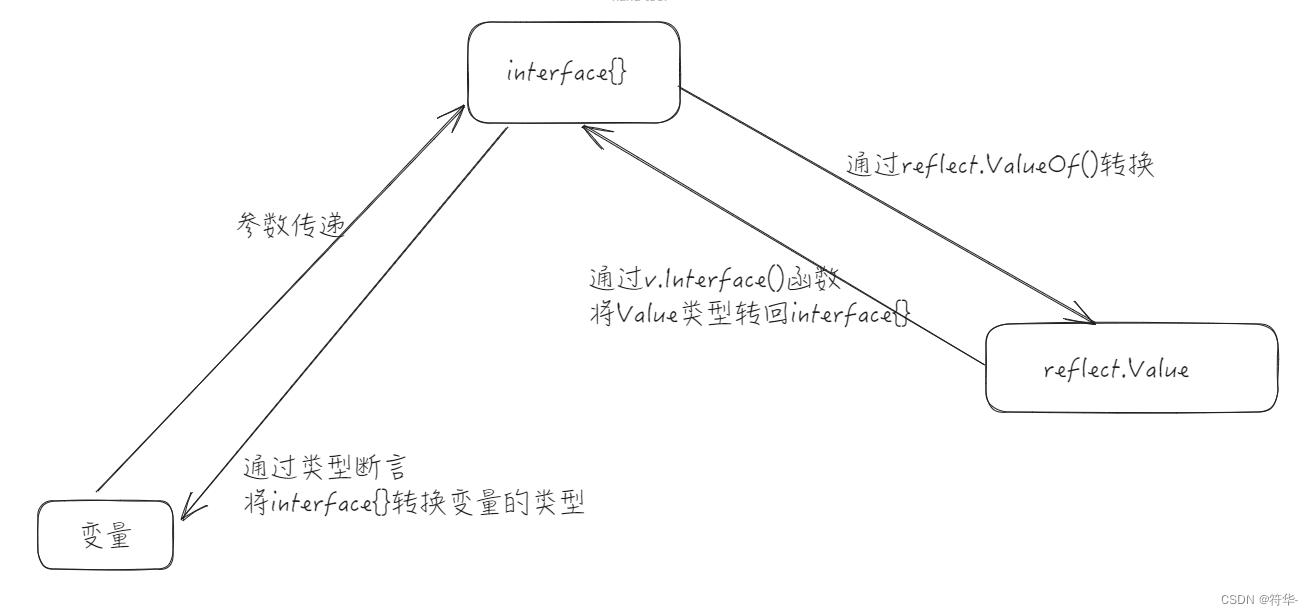
【Java转Go】快速上手学习笔记(四)之基础篇三
目录 泛型内置泛型的使用切片泛型和泛型函数map泛型泛型约束泛型完整代码 接口反射协程特点WaitGroupgoroutine的调度模型:MPG模型 channel介绍语法:举例:channel遍历基本使用和协程一起使用案例一案例二 select...casemain.go 完整代码 文件…...
vue中form和table标签过长
form标签过长 效果: 代码: <el-form-item v-for"(item,index) in ticketEditTable1" :label"item.fieldNameCn" :propitem.fieldName :key"item.fieldNameCn" overflow"":rules"form[item.fieldName…...
)
java基础复习(第七日)
java基础复习(七) 1.MQ如何避免消息重复投递或重复消费? 在消息生产时,MQ 内部针对每条生产者发送到消息生成一个 inner-msg-id,作为去重的依据(消息投递失败并重传),避免重复的消息进入队列;…...

day24 | 理论基础、77. 组合
目录: 解题及思路学习 理论基础 回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。 回溯法,一般可以…...
)
数据结构(1)
数据结构其实就是将数据按照一定的关系组织起来的集合,用于组织和存储数据。 1.数据结构分类 1.逻辑结构 逻辑结构是从具体问题中抽象出来的模型,是抽象意义的结构,按照对象中数据的相互关系进行分类。 1>集合结构:集合结构中…...

10个非常有用的Python库,你知道几个?
整理|TesterHome 这里给大家介绍10个不是最流行但非常有用的Python库,希望可以提供参考帮助。 PyO3 PyO3是一个Rust库,可以让你在Rust中编写Python模块。它可以利用 Rust 的速度和安全性编写高性能的 Python 模块。 https://github.com/PyO3…...
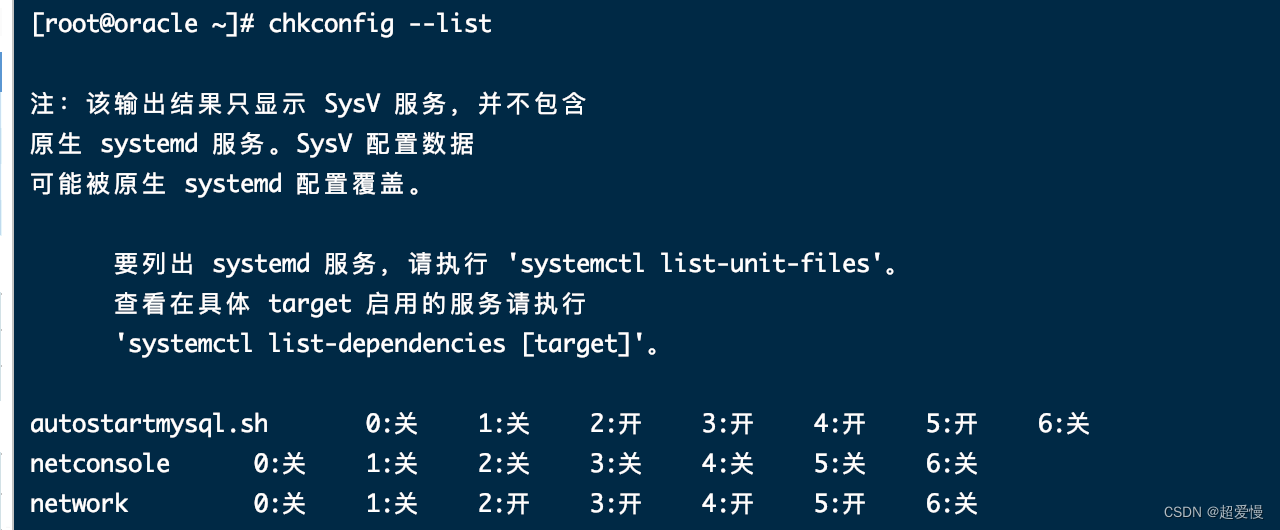
linux安装 MySQL8 并配置开机自启动
目录 1.下载 mysql 安装包 2.上传并解压 mysql 3.修改 mysql 文件夹名 4.创建mysql 用户和用户组 5.数据目录 (1)创建目录 (2)赋予权限 6.初始化mysql (1)配置参数 (2)配置环…...

MySQL视图
一、视图-介绍及基本语法 视图(View)是一种虚拟存在的表。视图中的数据并不在数据库中实际存在,行和列数据来自定义视图的查询中使用的表,并且是在使用视图时动态生成的。 通俗的讲,视图只保存了查询的SQL逻辑…...

Pytorch-day05-可视化-checkpoint
PyTorch 可视化 1、模型结构可视化2、训练过程可视化3、模型评估可视化 #导入常用包 import os import numpy as np import torch from torch import nn from torch.utils.data import Dataset, DataLoader from torchvision.transforms import transforms import torchvis…...

实训笔记8.23
8.23笔记 8.23笔记一、Hive中函数1.1 Hive中内置函数1.1.1 数学函数1.1.2 字符串函数1.1.3 日期函数1.1.4 条件函数1.1.5 特殊函数 1.2 Hive的自定义函数1.2.1 自定义UDF1.2.2 自定义UDTF 二、Hive的压缩机制三、数据同步工具Sqoop的安装和使用3.1 sqoop的概念3.2 sqoop的核心功…...

2023年菏泽市中职学校技能大赛“网络安全”赛项规程
2023年菏泽市中职学校技能大赛 “网络安全”赛项规程 一、赛项名称 赛项名称:网络安全 赛项所属专业大类:信息技术类 二、竞赛目的 通过竞赛,检验参赛选手对网络、服务器系统等网络空间中各个信息系统的安全防护能力,以及分析…...
Android 13 - Media框架(6)- NuPlayer
上一节我们通过 NuPlayerDriver 了解了 NuPlayer 的使用方式,这一节我们一起来学习 NuPlayer 的部分实现细节。 ps:之前用 NuPlayer 播放本地视频很多都无法播放,所以觉得它不太行,这两天重新阅读发现它的功能其实很全面ÿ…...

机器学习|DBSCAN 算法的数学原理及代码解析
机器学习|DBSCAN 算法的数学原理及代码解析 引言 聚类是机器学习领域中一项重要的任务,它可以将数据集中相似的样本归为一类。DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种是一种经典的密度聚类…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
