代码随想录算法训练营day38 | LeetCode 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
509. 斐波那契数(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台)
思路:经典的dp题。
int fib(int n){if(n == 0 || n == 1) return n;return fib(n-1) + fib(n-2);
}70. 爬楼梯(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台)
思路:直接用递归做会超时,说明不断地读写栈内存还是蛮耗时的。
int climbStairs(int n){if(n<3) return n;vector<int> dp(n+1, 0);dp[1] = 1;dp[2] = 2;for(int i=3; i<=n; i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];
}746. 使用最小花费爬楼梯(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台)
思路:一个套路,先确定状态转移公式,然后初始化,最后遍历一遍即可
int minCostClimbingStairs(vector<int>& cost) {int size = cost.size();vector<int> dp(size+1, 0);dp[0]=0;dp[1]=0;for(int i=2; i<size+1; i++){dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);}return dp[size];
}相关文章:

代码随想录算法训练营day38 | LeetCode 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
509. 斐波那契数(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台) 思路:经典的dp题。 int fib(int n){if(n 0 || n 1) return n;return fib(n-1) fib(n-2); } 70. 爬楼梯(题目…...

Linux基本指令【下】
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析3 目录 👉🏻cat👉🏻echo(输出…...
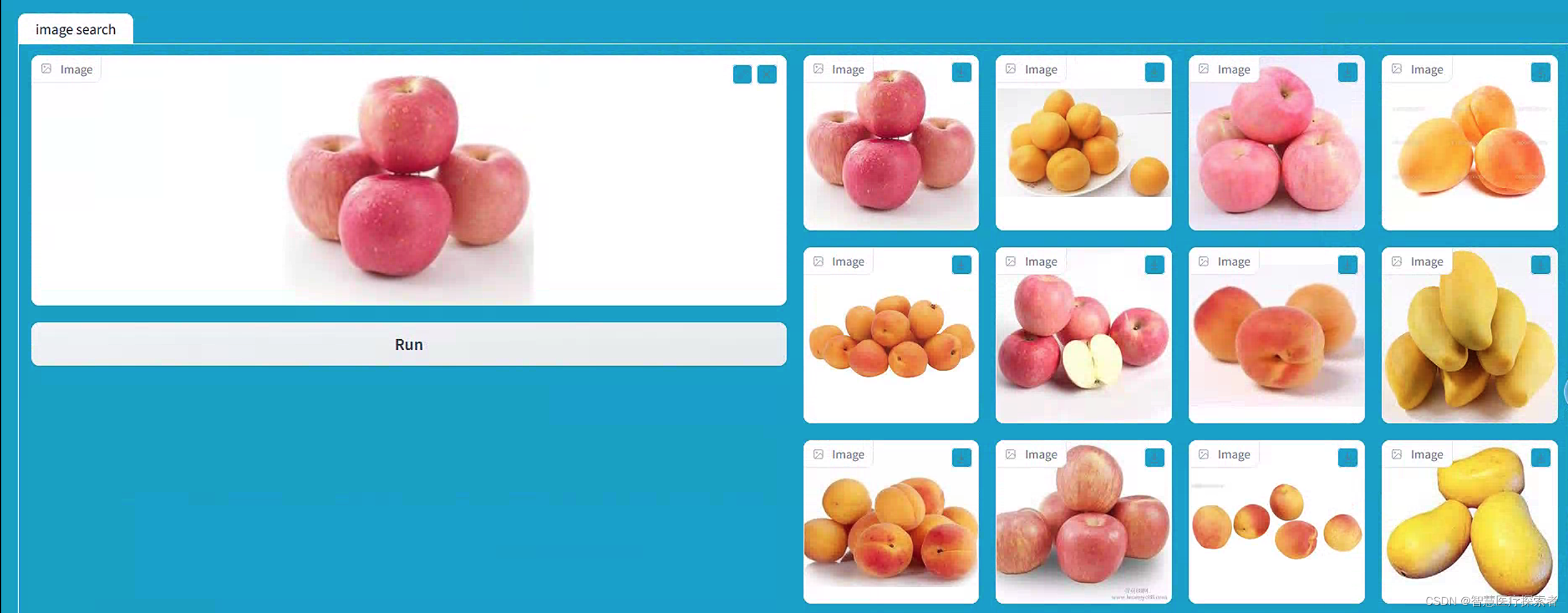
向量检索:基于ResNet预训练模型构建以图搜图系统
1 项目背景介绍 以图搜图是一种向量检索技术,通过上传一张图像来搜索并找到与之相关的其他图像或相关信息。以图搜图技术提供了一种更直观、更高效的信息检索方式。这种技术应用场景和价值非常广泛,经常会用在商品检索及购物、动植物识别、食品识别、知…...

SpringBoot 响应头添加版本号、打包项目后缀添加版本号和时间
文章目录 响应头添加版本号获取版本号添加响应处理器请求结果 打包项目后缀添加版本号和时间实现打包结果 响应头添加版本号 获取版本号 在 pom.xml 中,在 project.version 下定义版本号 在 application.yml 获取 pom.xml 中 project.version 中的信息 添加响应处…...

优化指南:带宽限制的可行策略
大家好!作为一名专业的爬虫程序员,我们经常面临的一个挑战就是带宽限制。尤其是在需要快速采集大量数据时,带宽限制成为了我们提升爬虫速度的一大阻碍。今天,我将和大家分享一些解决带宽限制的可行策略,希望能帮助大家…...

计算机提示mfc120u.dll缺失(找不到)怎么解决
在计算机领域,mfc120u.dll是一个重要的动态链接库文件。它包含了Microsoft Foundation Class (MFC) 库的特定版本,用于支持Windows操作系统中的应用程序开发。修复mfc120u.dll可能涉及到解决与该库相关的问题或错误。这可能包括程序崩溃、运行时错误或其…...
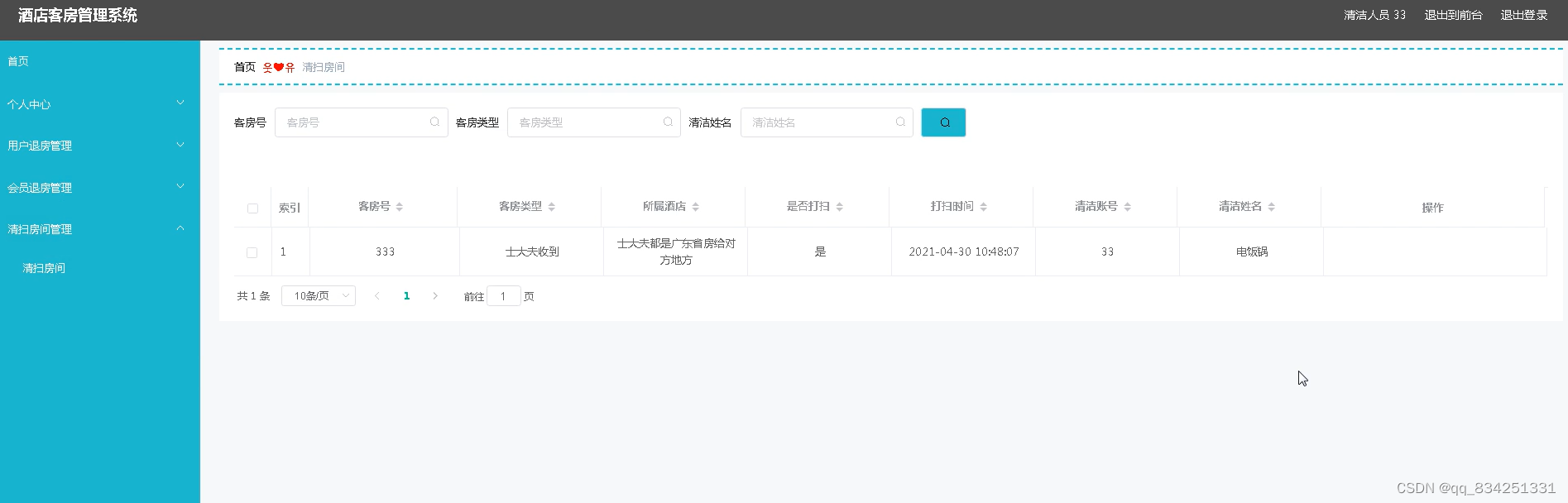
Java基于SpringBoot+Vue实现酒店客房管理系统(2.0 版本)
文章目录 一、前言介绍二、系统结构三、系统详细实现3.1用户信息管理3.2会员信息管理3.3客房信息管理3.4收藏客房管理3.5用户入住管理3.6客房清扫管理 四、部分核心代码 博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云…...
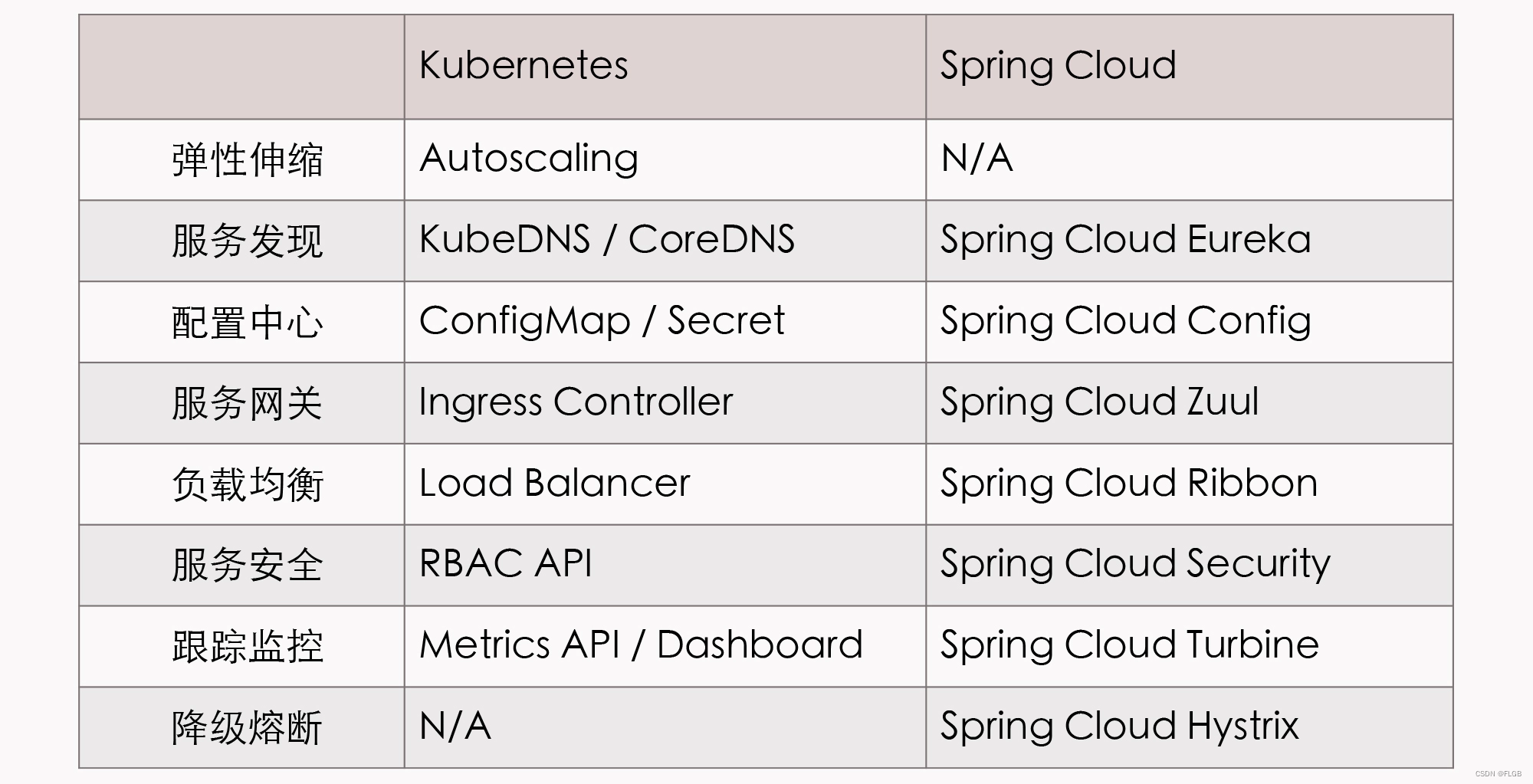
微服务架构2.0--云原生时代
云原生 云原生(Cloud Native)是一种关注于在云环境中构建、部署和管理应用程序的方法和理念。云原生应用能够最大程度地利用云计算基础设施的优势,如弹性、自动化、可伸缩性和高可用性。这个概念涵盖了许多方面,包括架构、开发、…...
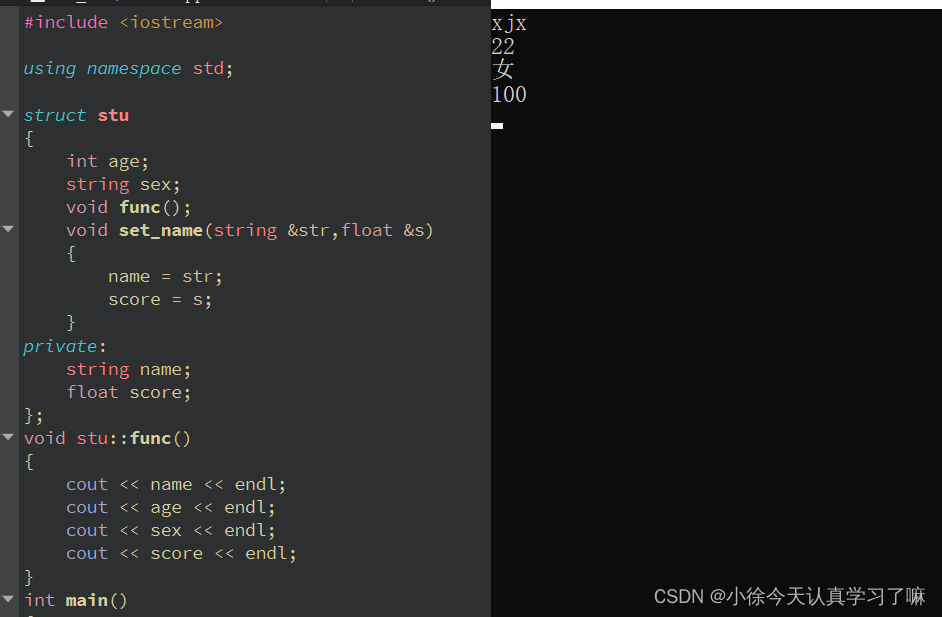
C++day2作业(2023.8.22)
1.定义一个学生的结构体,包含学生的姓名,年龄,成绩,性别,学生的成绩,姓名,定义为私有权限;定义一个学生类型的结构体变量,设置公有函数用于给学生的成绩和名字进行赋值&a…...

在 Spring Boot 中使用 OpenAI ChatGPT API
1、开始咯 我们来看看如何在 Spring Boot 中调用 OpenAI ChatGPT API。 我们将创建一个 Spring Boot 应用程序,该应用程序将通过调用 OpenAI ChatGPT API 生成对提示的响应。 2、OpenAI ChatGPT API 在开始具体讲解之前,让我们先探讨一下我们将在本教…...
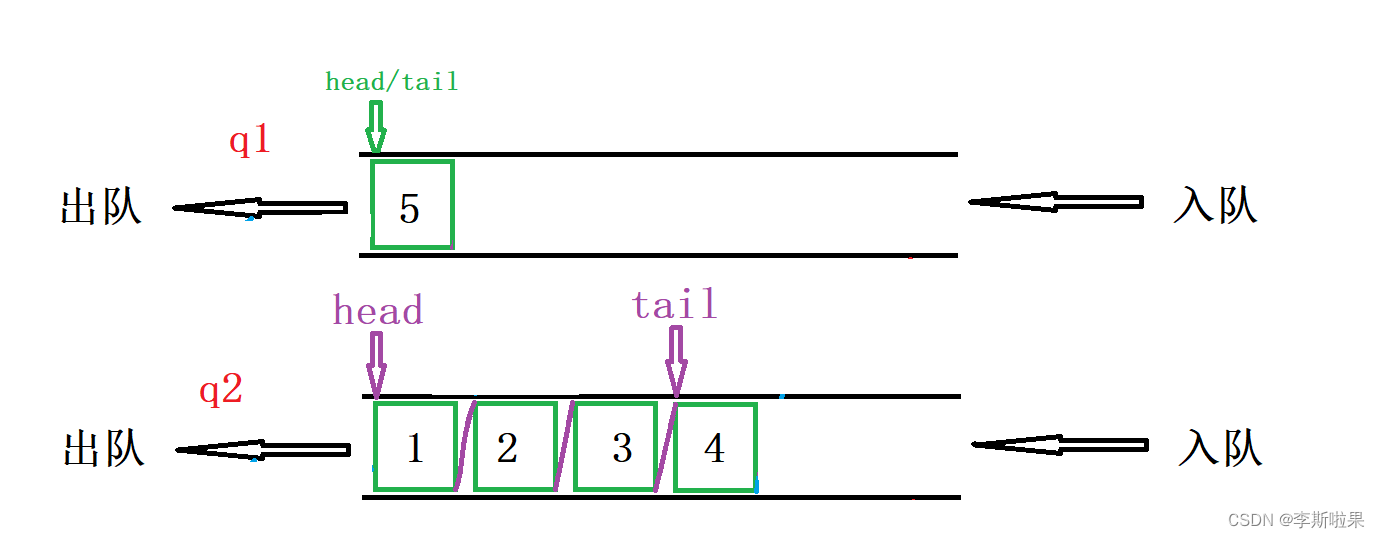
【leetcode】225.用队列实现栈
分析: 队列遵循先入先出的原则,栈遵循后入先出的原则 也就是说,使用队列实现栈时,入队操作正常,但是出队要模拟出栈的操作,我们需要访问的是队尾的元素;题目允许使用两个队列,我们可…...
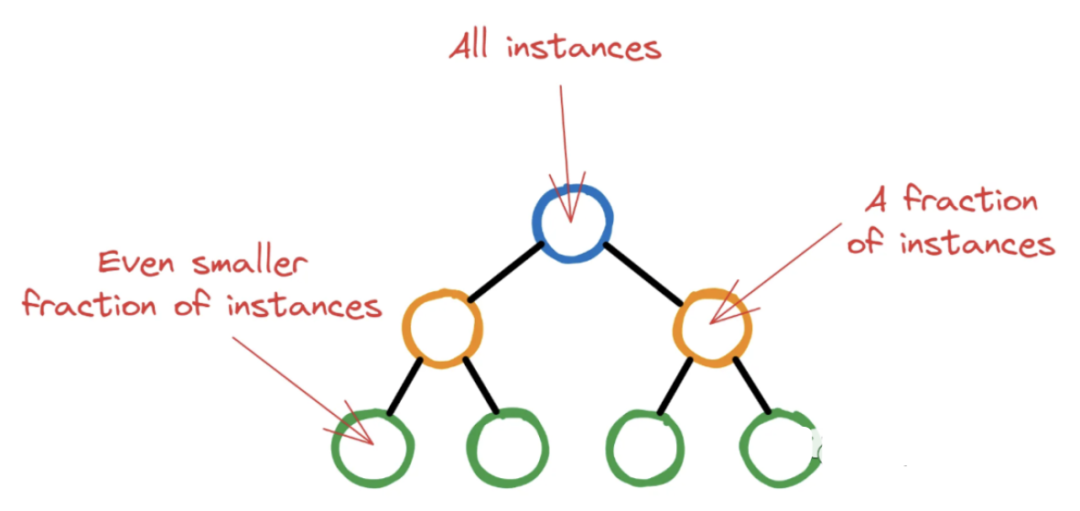
机器学习中XGBoost算法调参技巧
本文将详细解释XGBoost中十个最常用超参数的介绍,功能和值范围,及如何使用Optuna进行超参数调优。 对于XGBoost来说,默认的超参数是可以正常运行的,但是如果你想获得最佳的效果,那么就需要自行调整一些超参数来匹配你…...

第1章:计算机网络体系结构
文章目录 1.1 计算机网络 概述1.概念2.组成3.功能4.分类5.性能指标1.2 计算机网络 体系结构&参考模型1.分层结构2.协议、接口、服务3.ISO/OSI模型4.TCP/IP模型1.1 计算机网络 概述 1.概念 2.组成 1.组成部分&...
三(115))
【Java 动态数据统计图】动态数据统计思路Demo(动态,排序,containsKey)三(115)
上代码: import java.util.ArrayList; import java.util.HashMap; import java.util.Iterator; import java.util.LinkedList; import java.util.List; import java.util.Map;public class day10 {public static void main(String[] args) {List<Map<String,O…...

【游戏评测】河洛群侠传一周目玩后感
总游戏时长接近100小时,刚好一个月。 这两天费了点劲做了些成就,刷了等级,把最终决战做了。 总体感觉还是不错的。游戏是开放世界3D游戏,Unity引擎,瑕疵很多,但胜在剧情扎实,天赋系统、秘籍功法…...

java新特性之Lambda表达式
函数式编程 关注做什么,不关心是怎么实现的。为了实现该思想,java有了一种新的语法格式,Lambda表达式。Lambda本质是匿名内部类对象,是一个函数式接口。函数式接口表示接口内部只有一个抽象方法。使用该语法可以大大简化代码。 …...
向量组相关性与线性表示的性质,向量组的等价、极大线性无关组与秩)
【考研数学】线形代数第三章——向量 | 2)向量组相关性与线性表示的性质,向量组的等价、极大线性无关组与秩
文章目录 引言二、向量组的相关性与线性表示2.3 向量组相关性与线性表示的性质 三、向量组等价、向量组的极大线性无关组与秩3.1 基本概念 写在最后 引言 承接前文,我们来学习学习向量组相关性与线性表示的相关性质 二、向量组的相关性与线性表示 2.3 向量组相关性…...

Java中调用Linux脚本
在Java中,可以使用ProcessBuilder类来调用Linux脚本。以下是一个简单的示例,展示了如何在Java中调用Linux脚本: 创建一个Linux脚本文件(例如:myscript.sh),并在其中编写需要执行的命令。确保脚…...
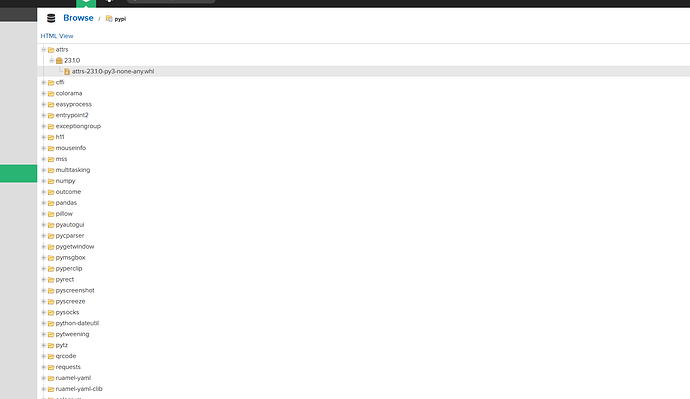
Nexus 如何配置 Python 的私有仓库
Nexus 可作为一个代理来使用。 针对一些网络环境不好的公司,可以通过配置 Nexus 来作为远程的代理。 Group 概念 Nexus 有一个 Group 的概念,我们可以认为一个 Nexus 仓库的 Group 就是很多不同的仓库的集合。 从下面的配置中我们可以看到࿰…...
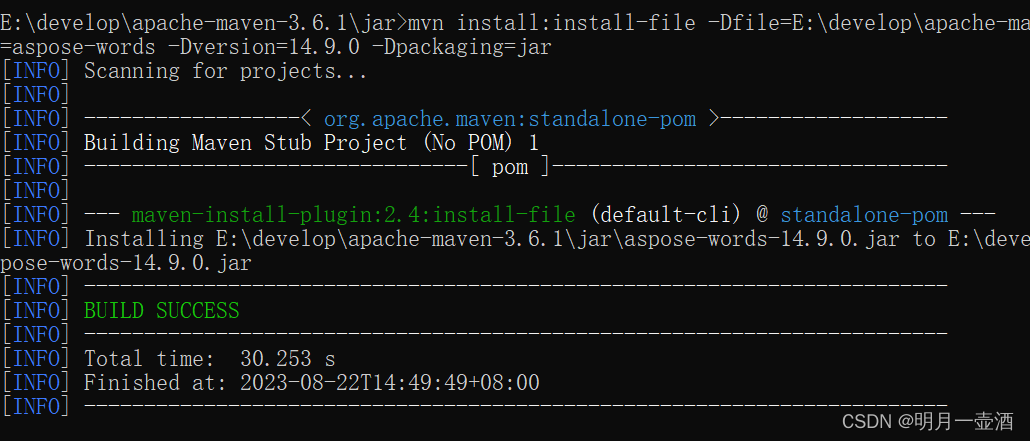
Maven 配置文件修改及导入第三方jar包
设置java和maven的环境变量 修改maven配置文件 (D:\app\apache-maven-3.5.0\conf\settings.xml,1中环境变量对应的maven包下的conf) 修改131行左右的mirror,设置阿里云的仓库地址 <mirror> <id>alimaven</id&g…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
