当前位置： 首页 > news >正文

PHP 高德地图，获取经纬度

news 2026/2/9 18:53:10 
function addresstolatlag($address){$abc = "xxx学校(xx路店)";$key="24fb21b484f89f212dc3f4fd016e2b4d";//没有key$address = $abc;$regeo_url="https://restapi.amap.com/v3/geocode/geo";$address_location=$regeo_url."?output=JSON&address=$address&key=$key";$data_location=file_get_contents($address_location);$arr_return=[];$result_local=json_decode($data_location,true);if($result_local['status'] == 1 && $result_local['infocode']== 10000){$location=$result_local['geocodes'][0]['location'];$arr=explode(',',$location);$arr_return['lat']=$arr[1];$arr_return['log']=$arr[0];}return $arr_return;
}

相关文章：

PHP 高德地图，获取经纬度

function addresstolatlag($address){$abc "xxx学校(xx路店)";$key"24fb21b484f89f212dc3f4fd016e2b4d";//没有key$address $abc;$regeo_url"https://restapi.amap.com/v3/geocode/geo";$address_location$regeo_url."?outputJSON&a…...

编程日记 2023/8/24 5:19:58

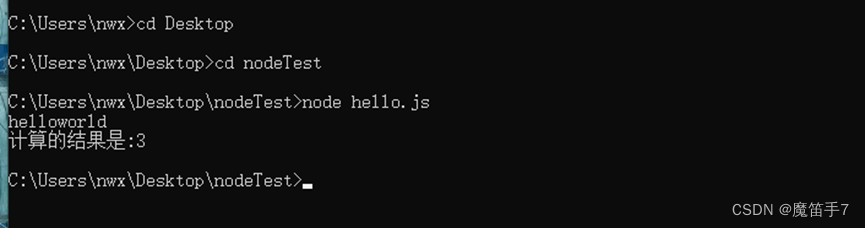
Node基础--Node基础使用体验

在上一篇文章中提到我们按照好Node.js之后，就可以在控制台看到其版本。那么下面我们一起来看看如何使用node执行js文件代码。 (1).在本地创建一个名称为hello.js的文件，输入内容如下所示: console.log("helloworld");var a 1;var b 2;cons…...

编程日记 2023/8/24 5:18:57

22 从0到1：API测试怎么做？常用API测试工具简介

API 测试的基本步骤 准备测试数据（可选，不一定所有 API 测试都需要这一步）；通过 API 测试工具，发起对被测 API 的 request；验证返回结果的 response。 Postman操作步骤 发起 API 调用；添加结…...

编程日记 2023/8/24 5:17:56

Skywalking Kafka Tracing实现

背景 Skywalking默认场景下，Tracing对于消息队列的发送场景，无法将TraceId传递到下游消费者，但对于微服务场景下，是有大量消息队列的业务场景的，这显然无法满足业务预期。 解决方案 Skywalking的官方社区中&#xf…...

编程日记 2023/8/24 5:16:55

Perl 解析字符串为日期对象并获取多天前的日期字符串

Perl 解析字符串 perl语言中的库 Time::Piece可以将字符串解析为日期对象。 use Time::Piece; my ($y, $m, $d) 20230823 ~ /^([0-9]{4})([0-9]{2})([0-9]{2})\z/ or die;my $dt Time::Piece->strptime("$y$m$d","%Y%m%d");Perl获取多天之前的日期 …...

编程日记 2023/8/24 5:15:54

C语言问题 - 关于一维数组和二维数组用*a+i形式表达

问题 今天在编写程序时被一个语句搞懵了&#xff1a; #include<stdio.h>int main() {int *pa[6];int a[2][3] {{1,2,3},{4,5,6}};int sum 0;int i,j,k 0;for (i0; i<2; i){for (j0; j<3; j){*(pa k) *(a i) j;k;}}for (i0; i<k; i){printf("%d &q…...

编程日记 2023/8/24 5:14:53

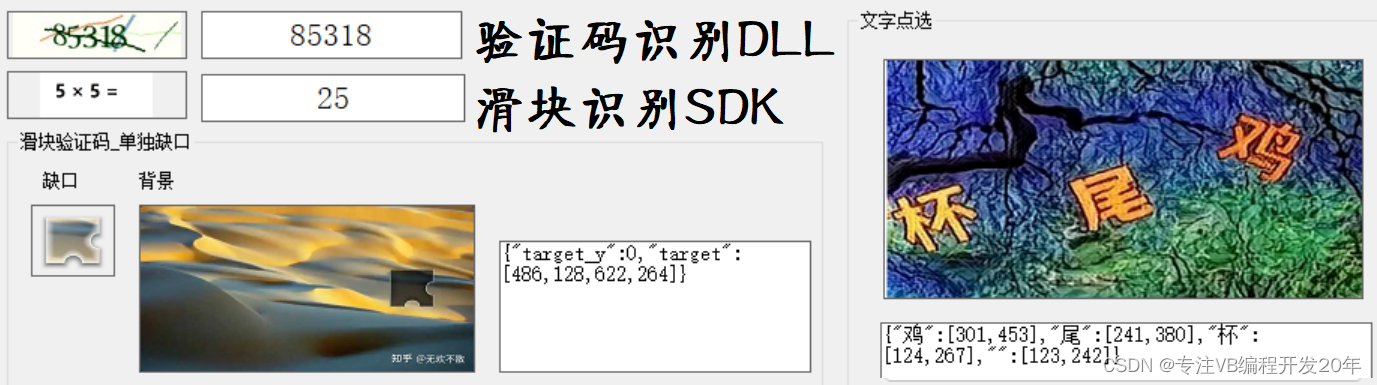
验证码识别DLL ,滑块识别SDK，OCR图片转文字，机器视觉找物品

验证码识别DLL ,滑块识别SDK 你们用过哪些OCR提取文字&#xff0c;识图DLL&#xff0c;比如Opencv,Labview机器视觉找物品之类&#xff1f;...

编程日记 2023/8/24 5:13:52

【图论】最小生成树的应用

一.题目 P1550 [USACO08OCT] Watering Hole G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 二.分析 1.我们是要使所有的农场都要有水 2.可以从起点引水&#xff0c;也可以互相引水。 3.费用要最小 这时我们可以想到最小生成树&#xff0c;建立一个虚拟节点即可。思路一…...

编程日记 2023/8/24 5:12:51

C++类模板的特化（三）

本文主要介绍类模板的特化、局部特化和缺省模板实参&#xff1b; 1.类模板的特化 类模板的特化&#xff08;Class Template Specialization&#xff09;是指为特定的模板参数提供自定义实现的过程。通过特化&#xff0c;我们可以针对某些特定的类型或条件提供不同的行为或实现…...

编程日记 2023/8/24 5:11:50

基于YOLOV8模型的课堂场景下人脸目标检测系统（PyTorch+Pyside6+YOLOv8模型）

摘要&#xff1a;基于YOLOV8模型的课堂场景下人脸目标检测系统可用于日常生活中检测与定位课堂场景下人脸&#xff0c;利用深度学习算法可实现图片、视频、摄像头等方式的目标检测&#xff0c;另外本系统还支持图片、视频等格式的结果可视化与结果导出。本系统采用YOLOv8目标检…...

编程日记 2023/8/24 5:10:49

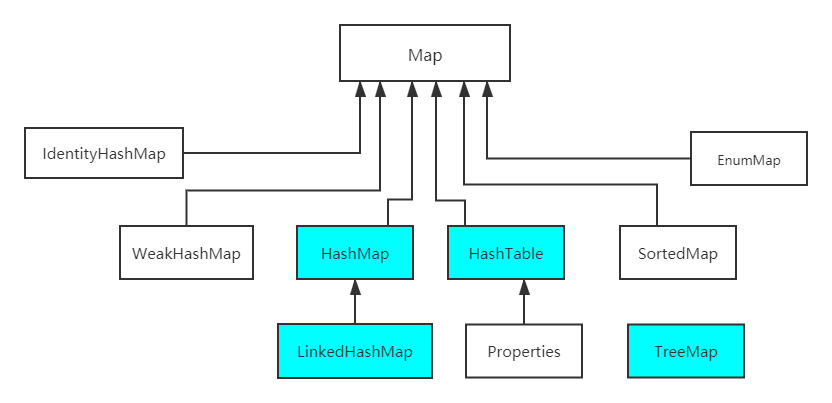
java八股文面试[数据结构]——Map有哪些子类

知识来源&#xff1a; 【23版面试突击】 用过哪些Map类&#xff0c;都有什么区别&#xff0c;HashMap是线程安全的吗&#xff1f;_哔哩哔哩_bilibili https://www.cnblogs.com/bubbleboom/p/12694013.html...

编程日记 2023/8/24 5:09:47

司徒理财：8.23今日黄金原油走势分析附操作策略

黄金走势分析&#xff1a; 　　 　　黄金下跌遇阻&#xff0c;短线开启震荡调整走势&#xff0c;但跌势依旧没有改变&#xff0c;没有突破1906压力前&#xff0c;还是偏空走势&#xff0c;反弹继续干空。趋势行情&#xff0c;不要轻言翻转&#xff01;即便下跌结束&#xff0c;…...

编程日记 2023/8/24 5:08:46

使用动态IP是否会影响网络

今天我们要谈论的话题是关于动态IP和网络的关系。也许有些小伙伴对这个概念还比较陌生&#xff0c;但别担心&#xff0c;我会简单明了的给你理清楚。让我们一起看看动态IP到底能否影响到网络。 首先&#xff0c;我们先来搞明白什么是动态IP。在互联网世界中&#xff0c;每一个连…...

编程日记 2023/8/24 5:07:45

Linux学习笔记-常用指令说明

本文目录 一、Linux指令笔记 二、"授人以鱼,不如授人以渔" 一、Linux指令笔记 0、cd 命令是 change dir 的简写&#xff0c;它可以把终端当前所在的路径切换至目标路径。 1、mkdir 建立文件夹。是 make directory 的简写&#xff0c;它可以在文件系统中创建一个新的目…...

编程日记 2023/8/24 5:06:44

MyBatisPlus进阶版

1.映射 1.1自动映射 【1】表名和实体类名映射 -> 表名user 实体类名User 【2】字段名和实体类属性名映射 -> 字段名name 实体类属性名name 【3】字段名下划线命名方式和实体类属性小驼峰命名方式映射 -> 字段名 user_email 实体类属性名 userEmail MybatisPlus…...

编程日记 2023/8/24 5:05:42

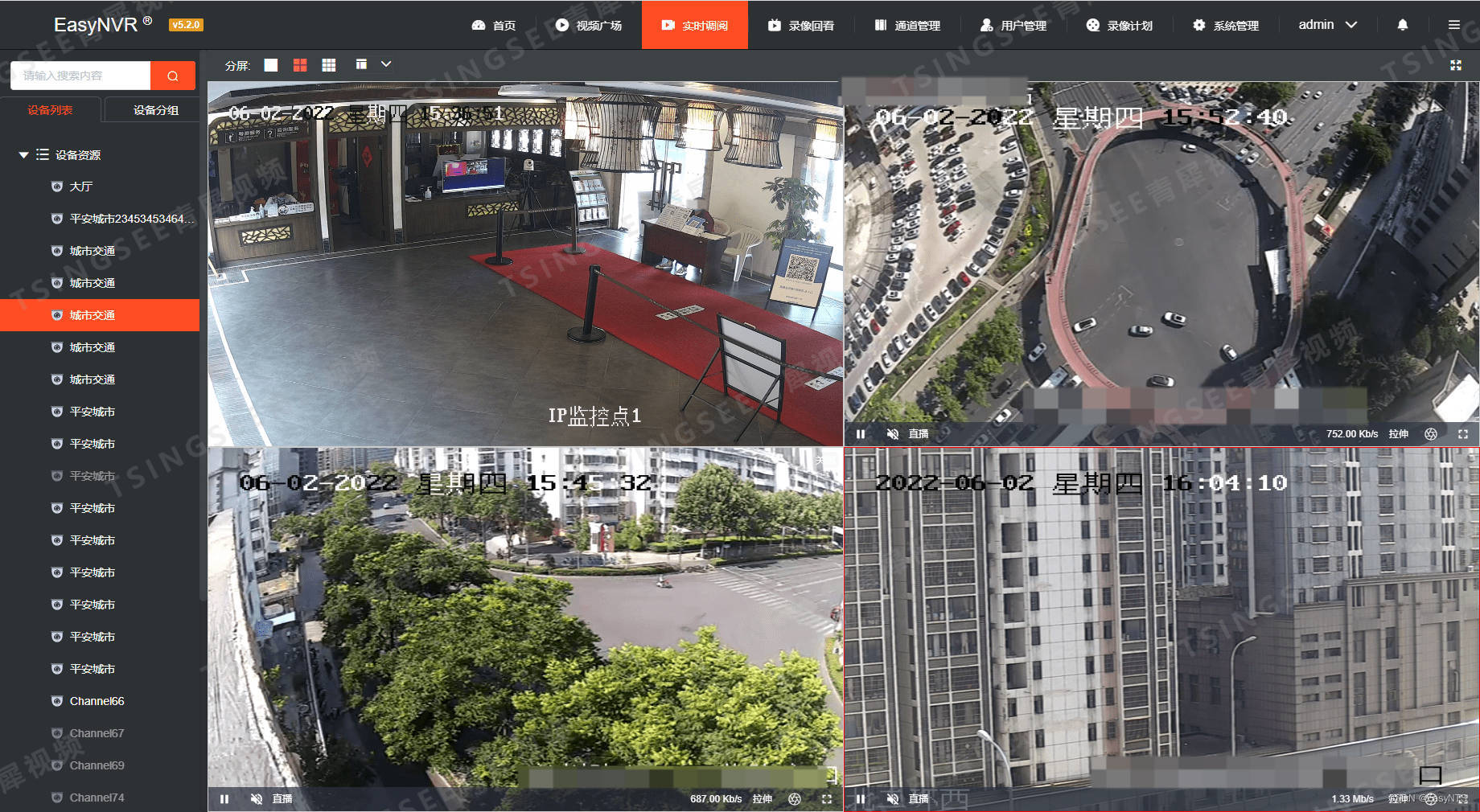
安防视频云平台EasyNVR视频汇聚平台硬件无法进入服务器的问题处理方法

EasyNVR是基于RTSP/Onvif协议的视频接入、处理及分发的安防视频云平台&#xff0c;可提供的视频能力包括&#xff1a;设备接入、实时视频直播、录像、云存储、录像回放与检索、告警、级联等&#xff0c;平台可支持将接入的视频流进行全平台、全终端的分发&#xff0c;分发的视频…...

编程日记 2023/8/24 5:04:41

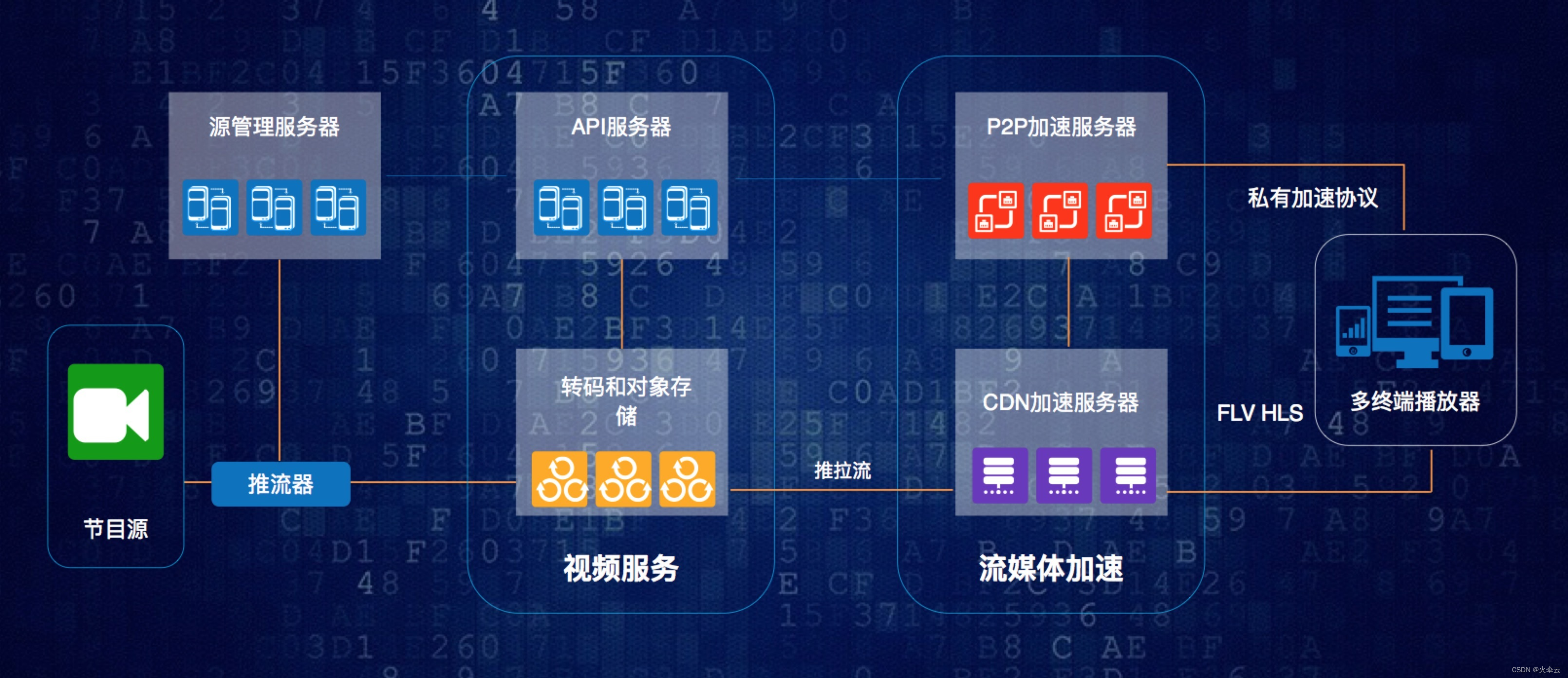
流媒体内容分发终极解决方案：当融合CDN与P2P视频交付结合

前言 随着互联网的发展&#xff0c;流媒体视频内容日趋增多&#xff0c;已经成为互联网信息的主要承载方式。相对传统的文字&#xff0c;图片等传统WEB应用&#xff0c;流媒体具有高数据量&#xff0c;高带宽、高访问量和高服务质量要求的特点&#xff0c;而现阶段互联网“尽力…...

编程日记 2023/8/24 5:03:38

根据源码，模拟实现 RabbitMQ - 内存数据管理(4)

目录 一、内存数据管理 1.1、需求分析 1.2、实现 MemoryDataCenter 类 1.2.1、ConcurrentHashMap 数据管理 1.2.2、封装交换机操作 1.2.3、封装队列操作 1.2.4、封装绑定操作 1.2.5、封装消息操作 1.2.6、封装未确认消息操作 1.2.7、封装恢复数据操作 一、内存数据管理…...

编程日记 2023/8/24 5:02:37

Apache Flume架构和原理

Apache Flume是一个开源的分布式、可靠的日志收集和聚合系统，旨在将大量的日志数据从不同的数据源（如应用程序、服务器、设备）收集到中心存储或数据湖中。Flume的架构设计允许用户在大规模数据流的情况下实现可靠的数据传输和处理。 Flume特性 Apache Flume是一个用于收集…...

编程日记 2023/8/24 5:01:36

代码随想录算法训练营day38 | LeetCode 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯

509. 斐波那契数&#xff08;题目链接&#xff1a;力扣&#xff08;LeetCode&#xff09;官网 - 全球极客挚爱的技术成长平台&#xff09; 思路&#xff1a;经典的dp题。 int fib(int n){if(n 0 || n 1) return n;return fib(n-1) fib(n-2); } 70. 爬楼梯&#xff08;题目…...

编程日记 2023/8/24 5:00:32

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

基于大模型的 UI 自动化系统

基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统，利用大模型实现智能 UI 自动化，结合计算机视觉和自然语言处理技术，实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

编程新知 2025/10/22 11:16:20

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序

一、开发准备 ​​环境搭建​​&#xff1a; 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 ​​项目创建​​&#xff1a; File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

编程新知 2025/9/5 12:16:40

【算法训练营Day07】字符串part1

文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接&#xff1a;344. 反转字符串 双指针法&#xff0c;两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

编程新知 2025/8/27 14:38:58

MODBUS TCP转CANopen 技术赋能高效协同作业

在现代工业自动化领域&#xff0c;MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步&#xff0c;这两种通讯协议也正在被逐步融合&#xff0c;形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

编程新知 2026/2/6 9:48:02

04-初识css

一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

编程新知 2026/1/29 17:54:05

C++中string流知识详解和示例

一、概览与类体系 C 提供三种基于内存字符串的流&#xff0c;定义在 <sstream> 中&#xff1a; std::istringstream&#xff1a;输入流&#xff0c;从已有字符串中读取并解析。std::ostringstream&#xff1a;输出流&#xff0c;向内部缓冲区写入内容&#xff0c;最终取…...

编程新知 2025/11/30 11:30:47

BCS 2025｜百度副总裁陈洋：智能体在安全领域的应用实践

6月5日&#xff0c;2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席&#xff0c;并作《智能体在安全领域的应用实践》主题演讲&#xff0c;分享了在智能体在安全领域的突破性实践。他指出&#xff0c;百度通过将安全能力…...

编程新知 2026/2/1 11:33:19

NFT模式：数字资产确权与链游经济系统构建

NFT模式&#xff1a;数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新&#xff1a;构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议&#xff1a;基于LayerZero协议实现以太坊、Solana等公链资产互通&#xff0c;通过零知…...

编程新知 2026/1/31 23:23:23

Fabric V2.5 通用溯源系统——增加图片上传与下载功能

fabric-trace项目在发布一年后，部署量已突破1000次，为支持更多场景，现新增支持图片信息上链，本文对图片上传、下载功能代码进行梳理，包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源，需要对底层数据结构进行修改，在此对智能合约中的农产品数…...

编程新知 2025/9/27 12:03:43